Using Machine Learning for IPM profile reconstruction

D. Vilsmeier, M. Sapinski and R. Singh

(d.vilsmeier@gsi.de)

Can we use Machine Learning for IPM profile reconstruction?

  • What is Machine Learning?
  • What is space-charge induced profile distortion?
  • How can we simulate this process?
  • What machine learning techniques can be applied?
  • How can we verify the simulation?
  • What's next?

What is Machine Learning?

Field of study that gives computers the ability to learn without being explicitly programmed.

- Arthur Samuel (1959)

"Classical"

approach:

+

=

Input

Algorithm

Output

Machine

Learning:

+

=

Input

Algorithm

Output

What is Machine Learning really?

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

- Tom Mitchell (1997)

+

=

Input

Algorithm

Output

Input

+

Output

Experience

Performance

Task

A Brief History of AI

Arthur Samuel

Checkers

1959

Minsky, Papert

Perceptron limits

1969

Hans Moravec

Autonomously driving car

1979

1992

TD-Gammon

Gerald Tesauro

1997

Deep Blue

IBM

2015

Playing Atari Games

DeepMind

2017

AlphaZero

DeepMind

Machine Learning Toolbox

Supervised Learning:

  • Artificial Neural Networks
  • Decision Trees
  • Linear Regression
  • k-Nearest Neighbor
  • Support Vector Machines
  • Random Forest
  • ... and many more

Unsupervised Learning:

  • k-Means Clustering
  • Autoencoders
  • Principal comp. analysis

Reinforcement Learning:

  • Q-Learning
  • Deep Deterministic Policy Gradient

Ionization Profile Monitors

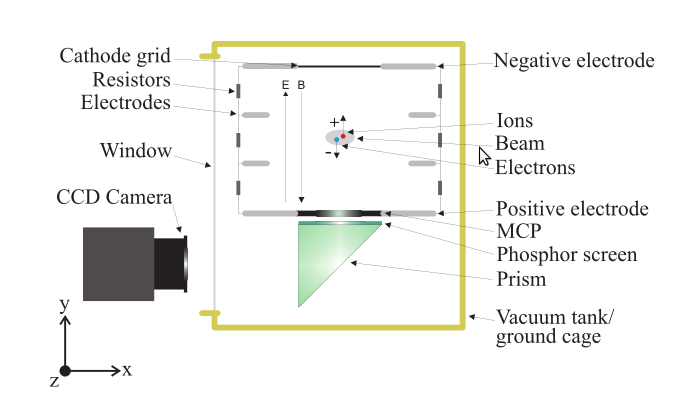
  • Measure the transverse profile of particle beams
  • Beam ionizes the rest gas
    🡒 measure the ionization products
  • Electric guiding field is used to transport ions / electrons to the detector
  • For electrons optionally apply a magnetic field to confine trajectories

The Problem

Extracting the ions / electrons from the ionization region is expected to provide a one-dimensional projection of the transverse beam profile, but ...

Protons
Energy 6.5 TeV
ppb 2.1e11
σ_x 0.27 mm
σ_y 0.36 mm
4σ_z 0.9 ns

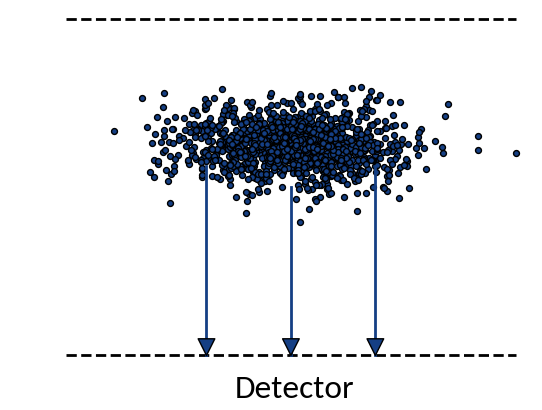
What happens?

Ideal case:

Particles move on straight lines towards the detector

Real case:

Trajectories are distorted due to various effects

IPM Profile Distortion

Initial momenta:
 

  • Initial velocity obtained in the ionization process may have a component along the profile
     
  • Becomes significant for small extraction fields / small beam sizes

Interaction with beam fields:

 

  • Close to the beam particles interact with the beam fields, resulting in distorted trajectories
     
  • Becomes significant for large beam fields, e.g. high charge densities or beam energies

+ instrumental effects such as camera tilt, point-spread-functions from optical system and multi-channel-plate granularity, etc.

Countermeasures

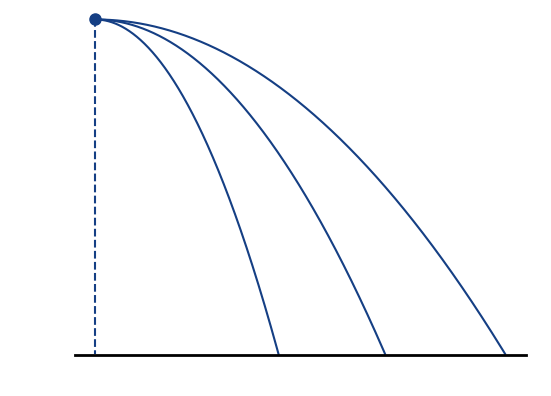
Increase electric guiding field

E_3 > E_2 > E_1

Increased electric field 🡒 smaller extraction times 🡒 smaller displacement

Additional magnetic guiding field

Increased magnetic field 🡒 smaller gyroradius 🡒 smaller possible displacement

B_1 \;\;\; < \;\;\; B_2

Space-charge interaction

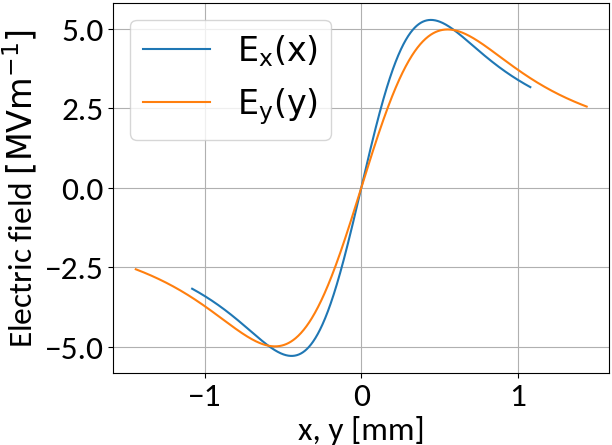
6.5 TeV, 2.1e11 Protons, σ = (270, 360) μm, 4σz = 0.9ns

  • Interaction with beam fields can become very strong 🡒 extraction fields are not sufficient to suppress distortion (typical values are 50 kV/m)
  • Space-charge interaction results in a vast increase of gyro-velocities and hence in large displacements

Space-charge interaction

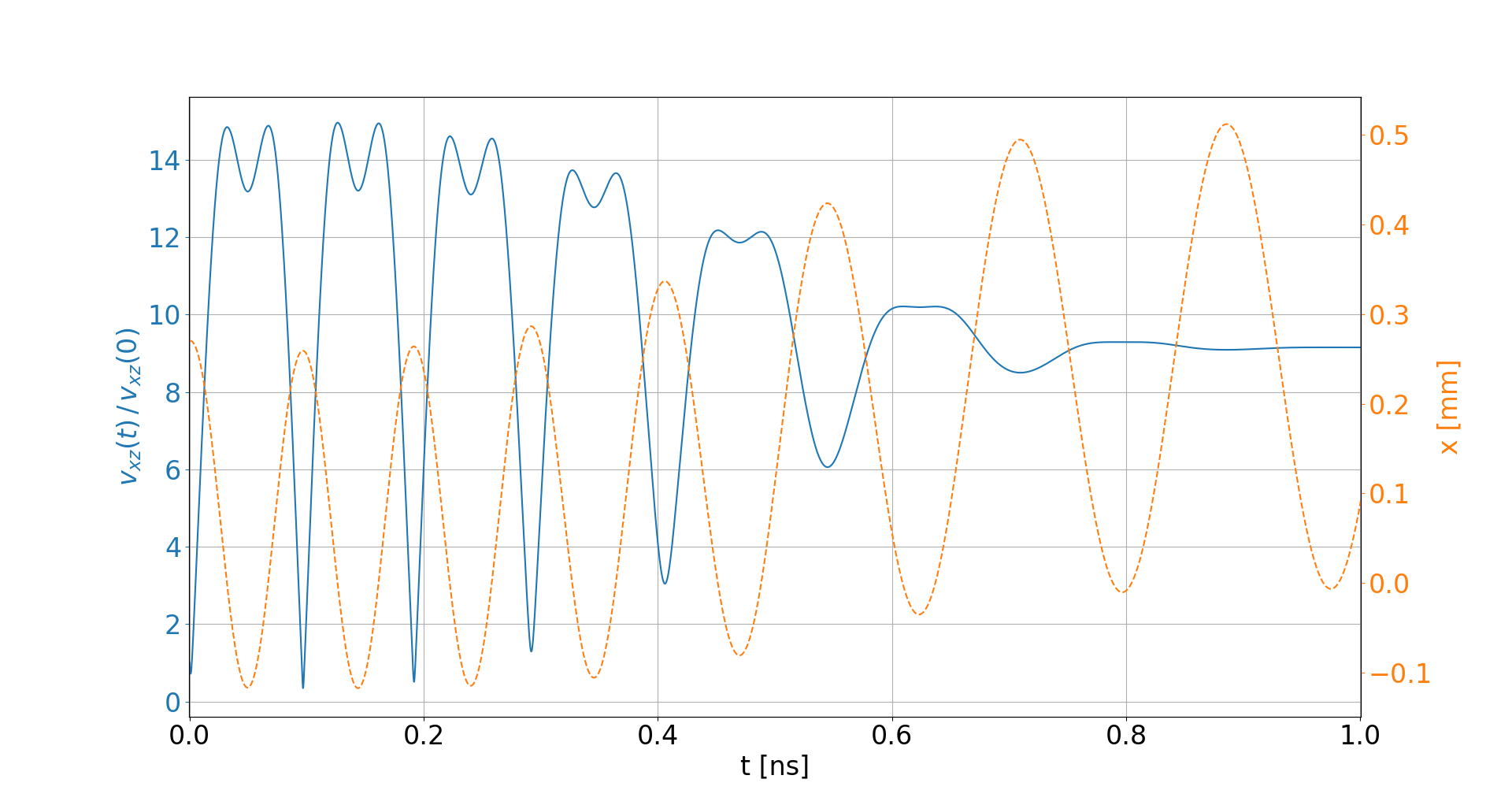
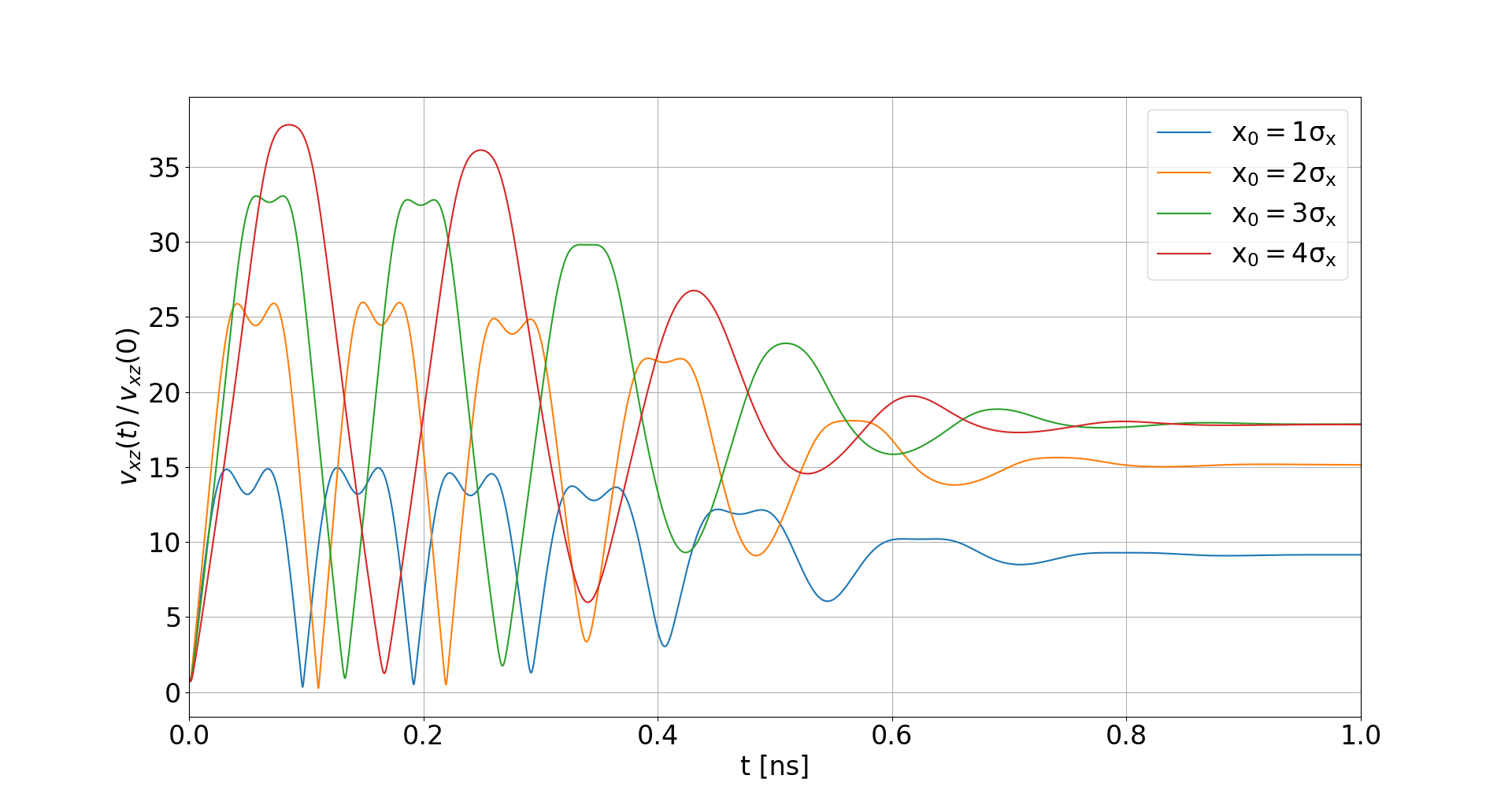
  • Electron velocities oscillate in the electric field of the beam
     
  • They level off at an increased velocity, hence increasing distortion
  • The amplitude of this oscillation depends on the initial offset to the beam center

Analytical considerations

Actually this type of oscillation can be seen from analytical considerations, using a simplified, namely linear, model for the beam electric field. This assumption holds well for the region close to the beam center.

 

The corresponding equations of motion are (for an electron):

\ddot{\vec{x}} = \frac{q}{m}\begin{pmatrix} E_0x - \dot{z}B \\ 0 \\ \dot{x}B \end{pmatrix} \;\; ,
\begin{aligned} 0 &< E_0 \\ q &< 0 \end{aligned}

Analytical considerations (II)

Defining

\bar{q} \equiv \frac{q}{m} \;\;\; , \;\;\; -\Omega^2 \equiv \bar{q}E_0 - \bar{q}^2B^2 < 0

One arrives at the following expressions for the velocity:

\begin{aligned} \dot{x}(t) &= v_{x0}\cos(\Omega t) - \frac{\bar{q}}{\Omega}(Bv_{z0} - Ex_0)\sin(\Omega t) \\ &\\ &\\ \dot{z}(t) &= \frac{\bar{q}B}{\Omega}v_{x0}\sin(\Omega t) + \frac{\bar{q}^2B}{\Omega^2}(Bv_{z0} - Ex_0)\cos(\Omega t) \\ &\\ & \;\; + \left( \frac{E}{B} + \frac{\bar{q}E}{\Omega^2B} \right)x_0 - \frac{\bar{q}E}{\Omega^2}v_{z0} \end{aligned}

What about particles that have their velocity decreased?

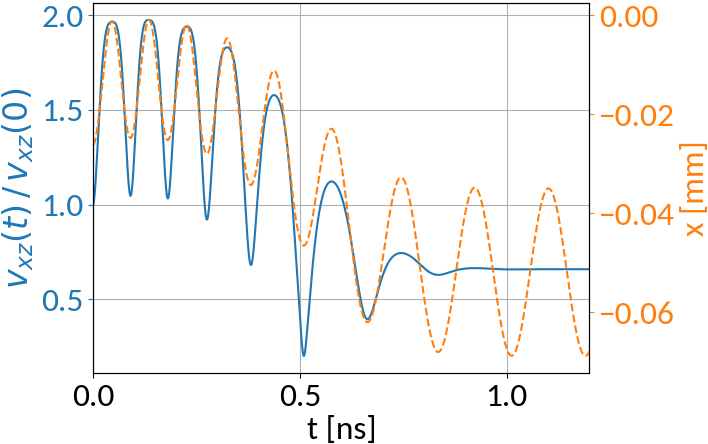
\vec{x}_0 = \begin{pmatrix} -0.097\sigma_x \\ -0.090\sigma_y \\ -0.5\sigma_z \end{pmatrix}, \vec{v}_0 = \begin{pmatrix} 85079 \\ 425128 \\ -897701 \end{pmatrix} \frac{m}{s}

Initial parameters:

\vec{x}_0 = \begin{pmatrix} 1\sigma_x \\ 0 \\ -0.5\sigma_z \end{pmatrix}, \vec{v}_0 = \begin{pmatrix} 707214 \\ 707214 \\ -707214 \end{pmatrix} \frac{m}{s}

Compare with particle that has its velocity increased:

Gyromotion

Space-charge region

Detector region

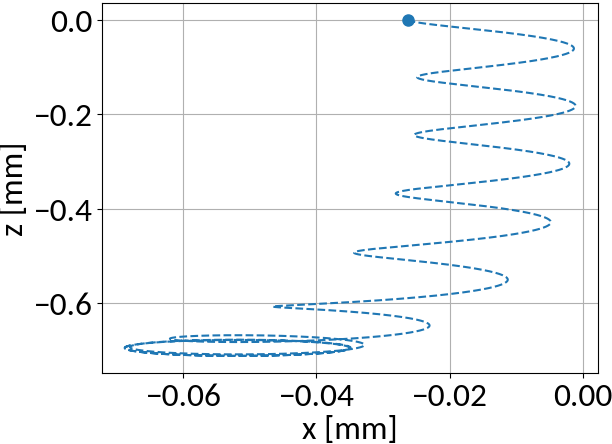
Electron motion is different for two distinct regions:

  • Space-charge region: beam field influences velocity
  • Detector region: pure gyromotion without beam field influence

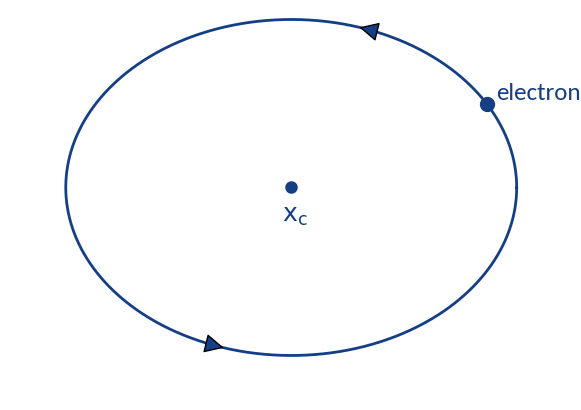
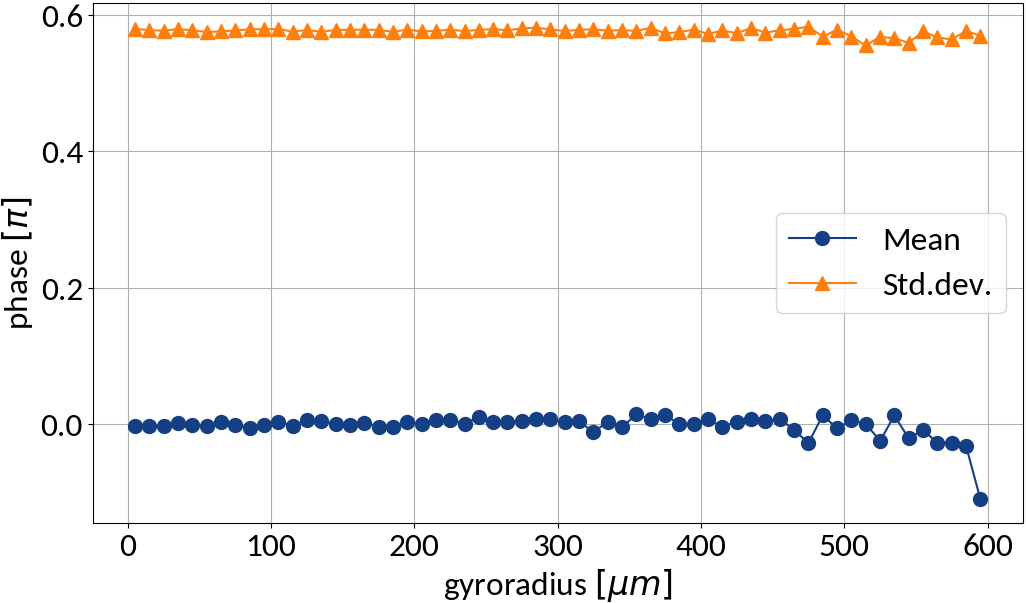
Distortion through gyromotion

Gyromotion is parametrized via

\begin{aligned} x(t) &= \frac{v_{x0}}{\omega}\sin(\omega t) + \frac{v_{z0}}{\omega}\cos(\omega t) + \left( x_0 - \frac{v_{z0}}{\omega} \right) \\ &\\ z(t) &= -\frac{v_{x0}}{\omega}\cos(\omega t) + \frac{v_{z0}}{\omega}\sin(\omega t) + \left( z_0 + \frac{v_{x0}}{\omega} \right) \end{aligned}

Particle spirals around
 

and will be detected in the range

x_c = x_0 - \frac{v_{z0}}{\omega}
x_c \pm \frac{\sqrt{v_{x0}^2 + v_{z0}^2}}{\omega}

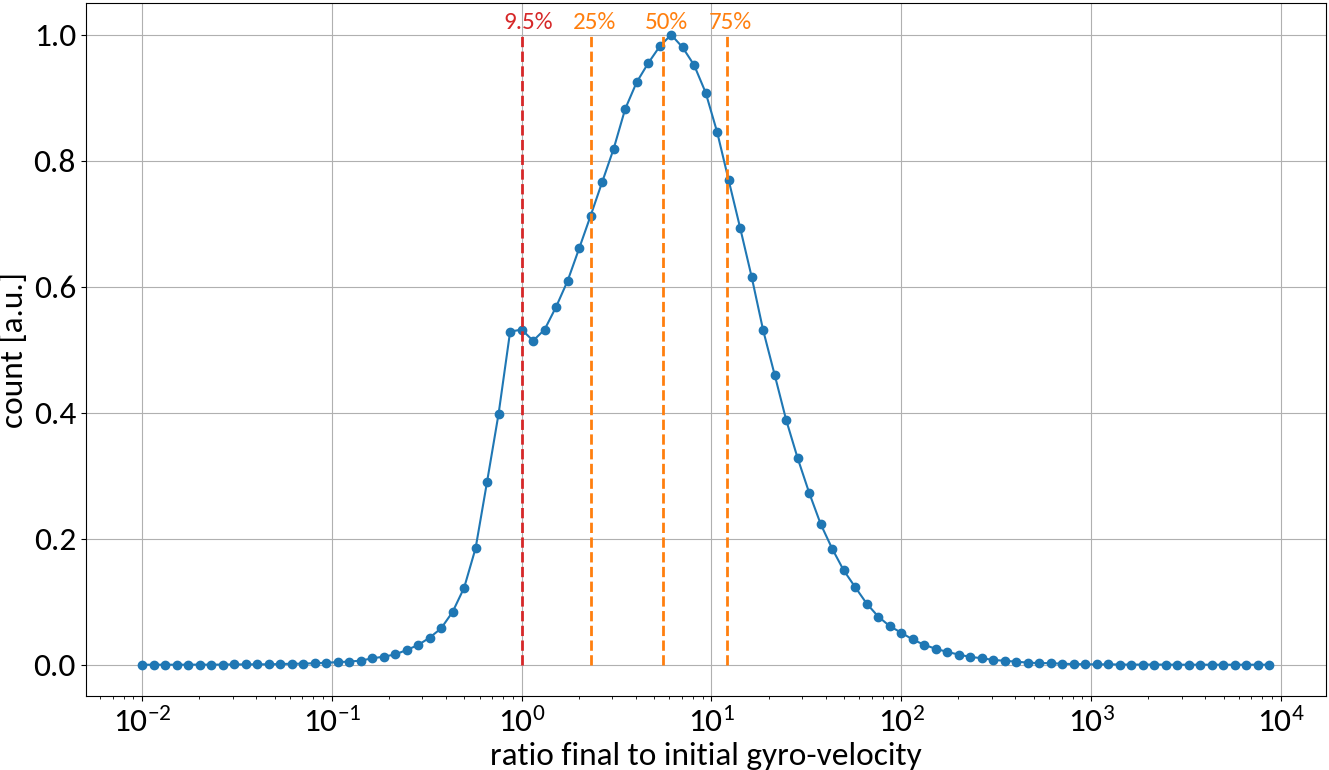
Detection probabilities

Provided that the moment of detection is random, the gyromotion of electrons gives rise to probabilities of being detected at a specific position.

p(x) \propto \lvert \lim_{\Delta x \rightarrow 0} \frac{1}{\Delta x} \int_{x}^{x + \Delta x} ds \rvert = \frac{1}{\sqrt{R^2 - (x - x_c)^2}}

Applying the limit results in divergence at the "edges" of the motion, so the expression is only valid for the center. For real profiles however we can work with a discretized version of the abovementioned relation.

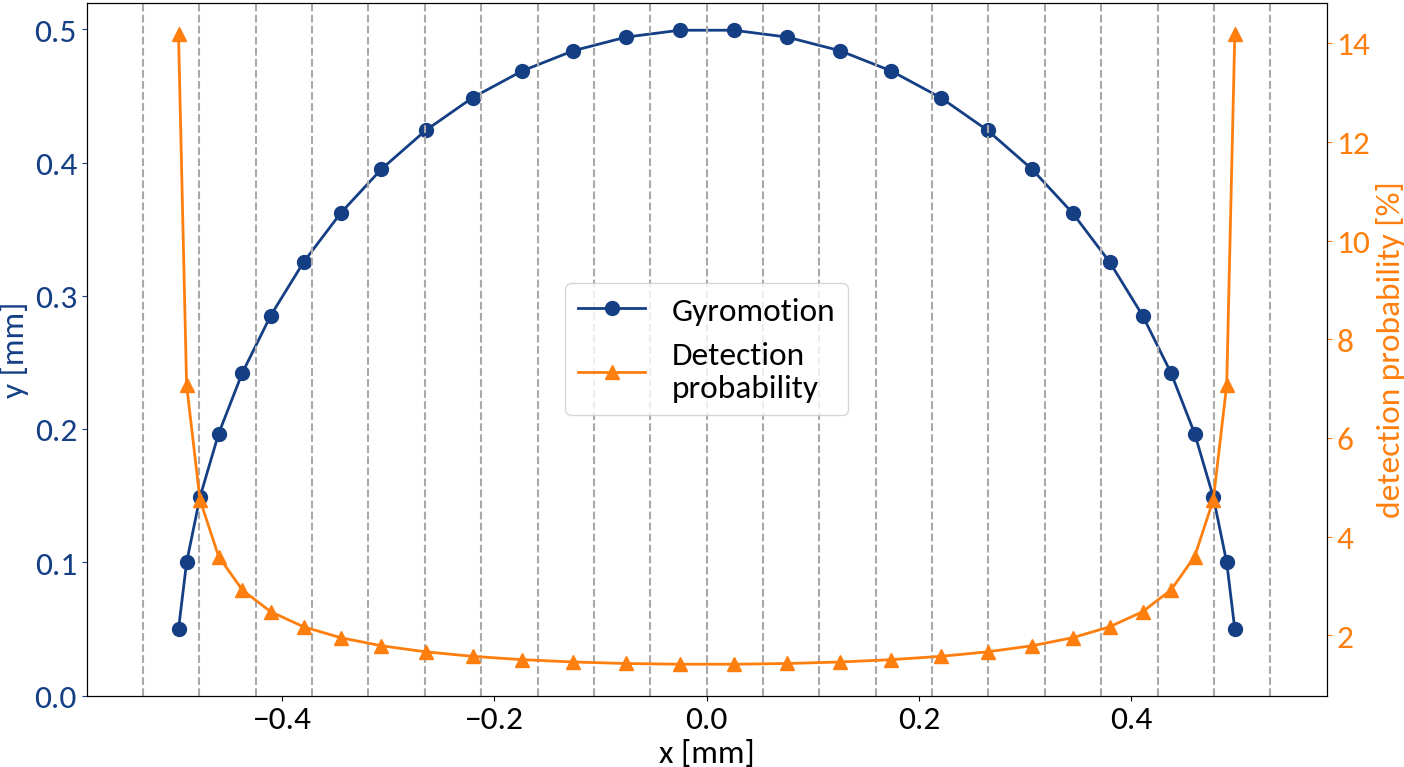
small statistics

Summary of displacements

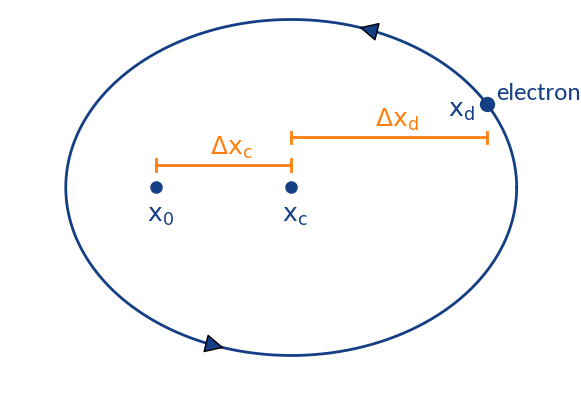
-  position at ionization

-  gyration center (detector region)

-  position of detection

x_0
x_c
x_d

Two types of displacement:

 

  •         : Depends on initial z-velocity, transverse electric field, ExB-drift by long. electric field
     
  •         : Displacement due to gyration motion; stochastic displacement
\Delta x_c
\Delta x_d

Analytical description?

In principal z-velocities are relatively small (shift ~ 10 μm; ionized electrons are mainly scattered in transverse direction), the longitudinal electric field can be neglected and the center shift due to the transverse electric field is around a few micrometers which is small compared to the magnitude of the gyro-motion.

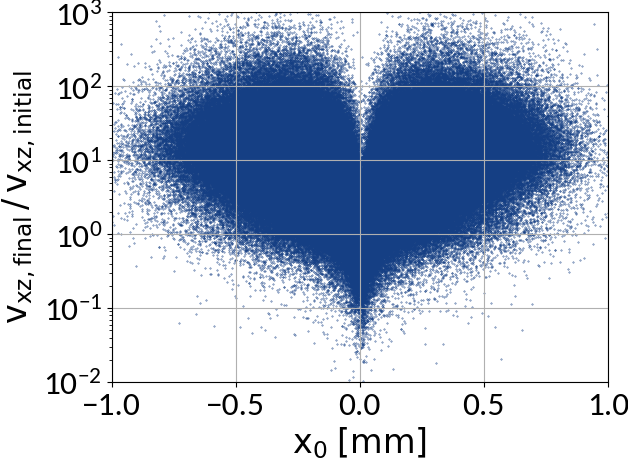
Describing the gyro-distortion via point-spread-functions is however not possible because the gyro-velocity increase is not uniform along the profile.

Simulating the process

https://gitlab.com/IPMsim/Virtual-IPM

https://pypi.org/project/virtual-ipm

Virtual-IPM simulation tool was used to generate the data

Parameter Range Step size
Bunch pop. [1e11] 1.1 -- 2.1 ppb 0.1 ppb
Bunch width (1σ) 270 -- 370 μm 5 μm
Bunch height (1σ) 360 -- 600 μm 20 μm
Bunch length (4σ) 0.9 -- 1.2 ns 0.05 ns

Protons

6.5 TeV

4kV / 85mm

0.2 T

  =  21,021 cases  |  5h / case  |  12 yrs  |     Good thing there are computing clusters :-)

Physics models

Analytical expression for the electric field of a two-dimensional Gaussian charge distribution

🡒 Longitudinal field is neglected; justifiable for highly relativistic beam

🡒 Magnetic field is considered

M. Bassetti and G.A. Erskine, "Closed expression for the electrical field of a two-dimensional Gaussian charge", CERN-ISR-TH/80-06, 1980

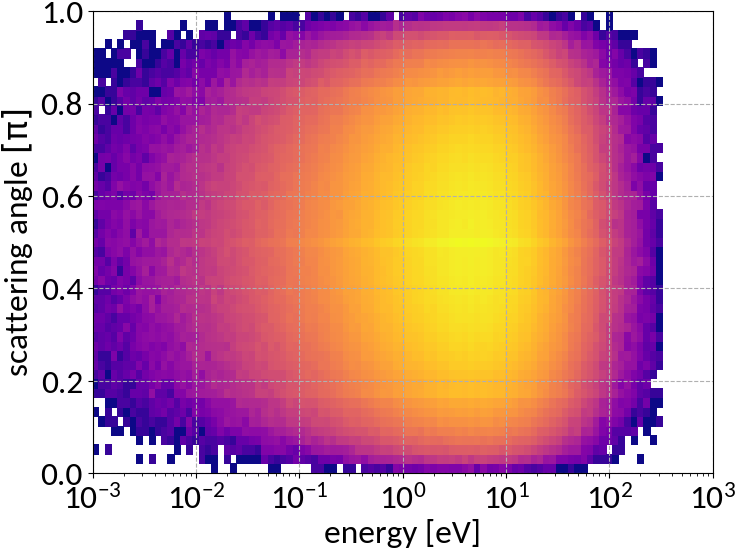
Double differential cross section for relativistic incident particles

A. Voitkiv et al, "Hydrogen and helium ionization by relativistic projectiles in collisions with small momentum transfer", J.Phys.B: At.Mol.Opt.Phys, vol.32, 1999

Uniform electric and magnetic guiding fields

Simulated profiles

Simulation outputs particle parameters as csv data frame

Summarize initial and final positions into  1 μm histograms ranging [-10, 10] mm

Rebin to 55 μm (silicon pixel detector) and 100 μm (optical acquisition system)

Bunch population and bunch length

&

Data preparation

ppb 4σz f [1] ... f [n] i [1] ... i [n]

Data

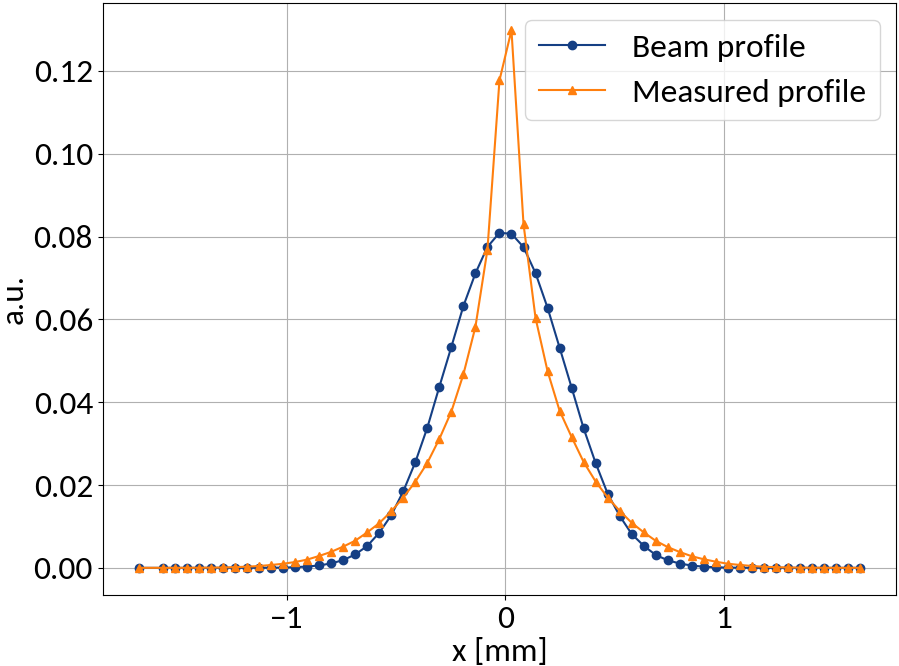
Measured profile

Beam profile

Input

Output

Drop zero variance variables (as they don't provide any information)

Rescale data to have zero mean and unit variance:                       

x \rightarrow (x - \mu) / \sigma

Compute σ from profile

Optionally rescale

(\;\;\;\;\;\;)

Train, Test, Validate

Divide the machine "learning" into three stages and corresponding data sets:

Training

Validation

Testing

This data set is used to derive rules from the data, i.e. to fit the model (e.g. polynomial fit). Split size ~ 60%.

This data set is used to ensure that the model generalizes well to unseen data, between multiple iterations of hyper-parameter tuning (e.g. polynomial degree) and model selection. Split size ~ 20%.

This data set is used for evaluating the performance of the final model (in order to prevent "tuning-bias"). Split size ~ 20%.

Evaluating performance

Explained variance

1 - \frac{Var\left[ y_{true} - y_{pred} \right]}{Var\left[ y_{true} \right]}

Mean squared error

\frac{1}{N}\Sigma\left( y_{true} - y_{pred} \right)^2

R2-score

1 - \frac{\Sigma\left( y_{true} - y_{pred} \right)^2}{\Sigma\left( y_{true} - \mu_{true} \right)^2}

Anscombe's quartet

 

Similar mean, variance and R2 (approx.)

 

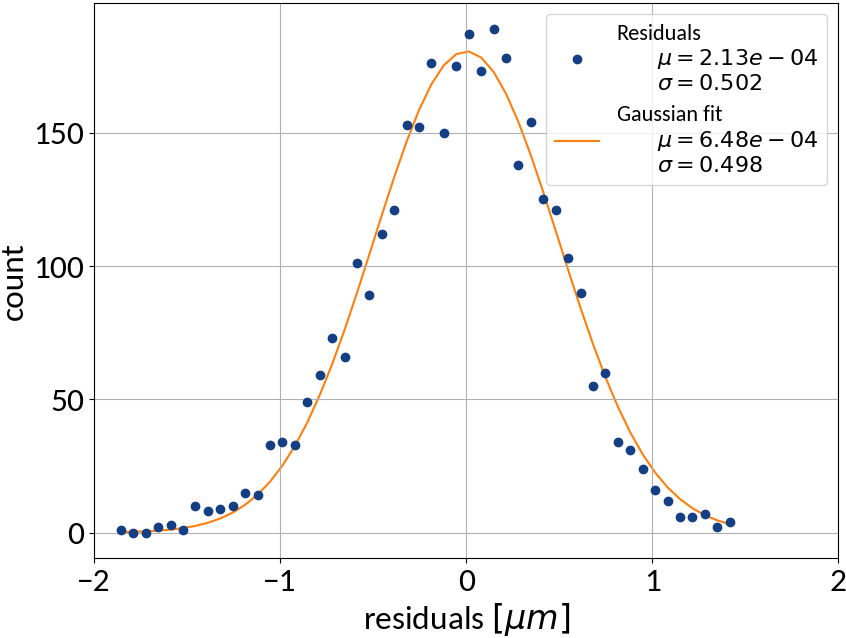
Residuals plot is important

 

Visualization helps in assessing the quality of a model

https://commons.wikimedia.org/wiki/File:Anscombe.svg

Multivariable linear regression

\sigma_x = \vec{\beta}^{\,T}\vec{x} + b + \epsilon

Requirements:

  • Predictors are error-free
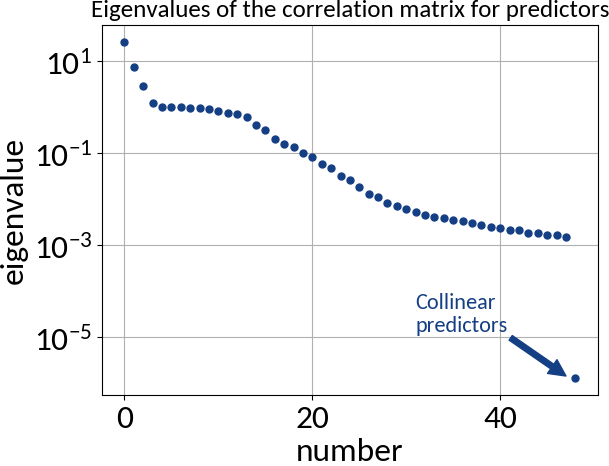
  • Absence of multi-collinearity among the predictors

predictors

intercept

error term

Multivariable linear regression - Results

Explained variance 0.99972
R2-score 0.99972
Mean squared error 0.25212
\mu m^2

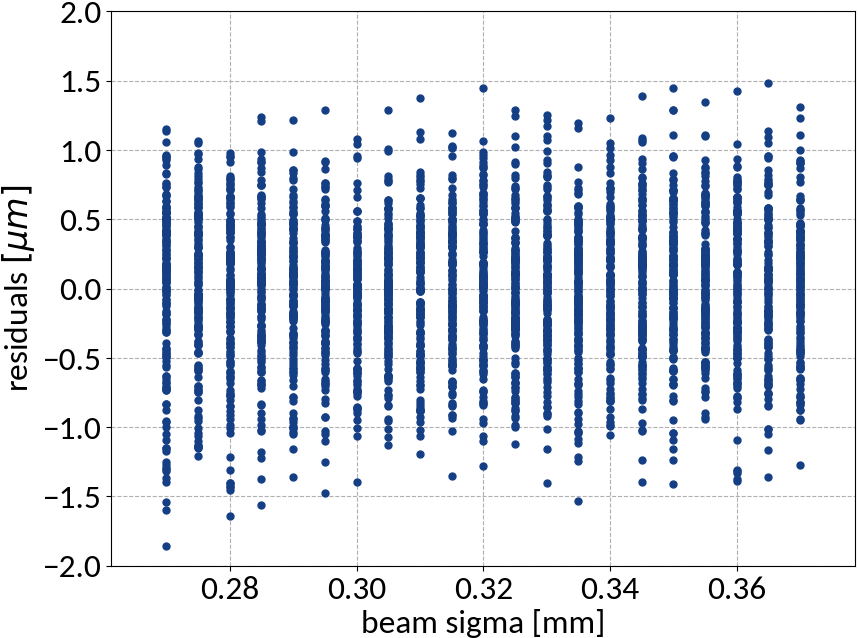
Kernel ridge regression

Twofold extension of "classical" linear regression:

  • Uses ridge regularization for the learned weights (L2-norm)
  • Employs the "Kernel trick"
L = \frac{1}{2}\Sigma_i \left( y_{i, true} - y_{i, pred} \right)^2 + \frac{1}{2}\lambda\left|\left|w\right|\right|^2

L2 "ridge" regularization:

Adding the norm of the weights to the loss function puts a penalty on the weights.

Strength of penalization can be adjusted.

Regularization term prevents overfitting

The Kernel Trick

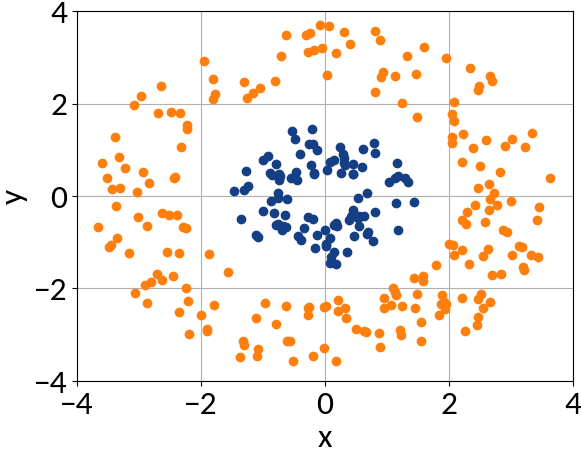
Features can't be separated by a linear function ...

... at least not in two-dimensional space.

Define a mapping, for example:

\begin{aligned} & K: \mathbb{R}^2 \rightarrow \mathbb{R}^3 \\ & K(x, y) = \left( x, y, x^2 + y^2 \right) \end{aligned}

Now the space in which K maps may be very high dimensional, so computing the corresponding vectors is expensive.

The trick is to express the dot product of K(x, y) in terms of the initial vectors (x, y) 🡒 no need to compute K(x, y).

Kernel ridge regression - Results

Polynomial kernel

K(x, y) = \left(x^Ty + c\right)^2

Radial basis function kernel

K(x, y) = \exp\left( -\gamma || x - y || \right)
\alpha = 0.001

degree = 2

\alpha = 0.001
\gamma = 0.0002
Poly kernel RBF kernel
Explained variance 0.99983 0.99974
R2-score 0.99983 0.99974
Mean squared error 0.15074 0.23331
\mu m^2
\mu m^2

Support Vector Machine

  • Originally developed for classification tasks
  • Find a linear separation of two classes with maximum margin between them
\hat{y} = sgn\left( \sum_i \alpha_i y_i \vec{x}_i\cdot\hat{\vec{x}} + b \right)

prediction

learned weights

class labels

training data

intercept of hyperplane

Fitting and predicting only depends on dot products of feature vectors, so we can use the kernel trick

https://commons.wikimedia.org/wiki/File:Svm_max_sep_hyperplane_with_margin.png

Support Vector Regression

SVM

hinge loss

SVR

ε-insensitive loss

\max\left( 0, 1 - y_i\cdot f(x_i) \right)
\max\left( 0, \lvert y_i - f(x_i) \rvert - \epsilon \right)

The fitted model is similar to Kernel Ridge Regression but the loss function is different (KRR uses ordinary least squares)

y(x) = \sum_i \alpha_i K(x_i, x) + b

Support Vector Regression - Results

Explained variance 0.99985
R2-score 0.99985
Mean squared error 0.13527
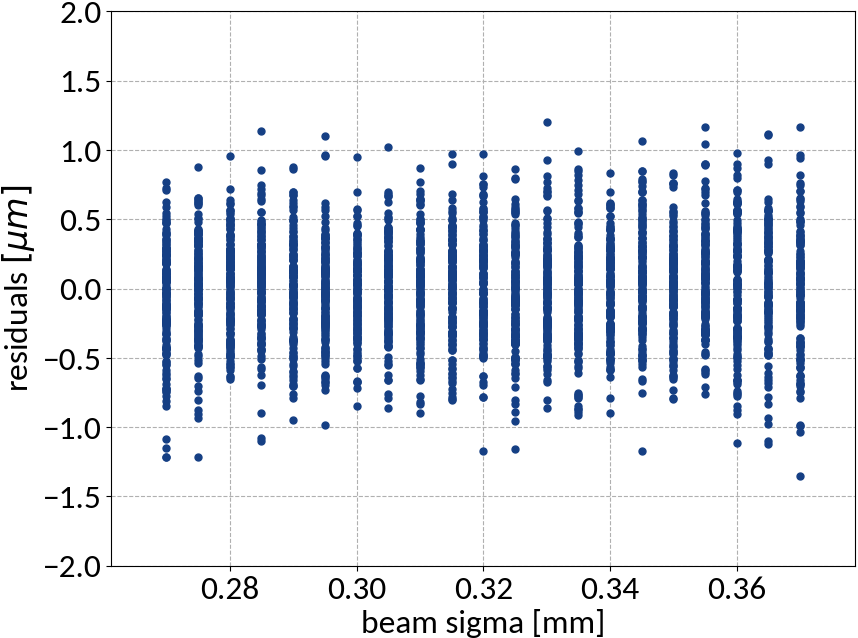
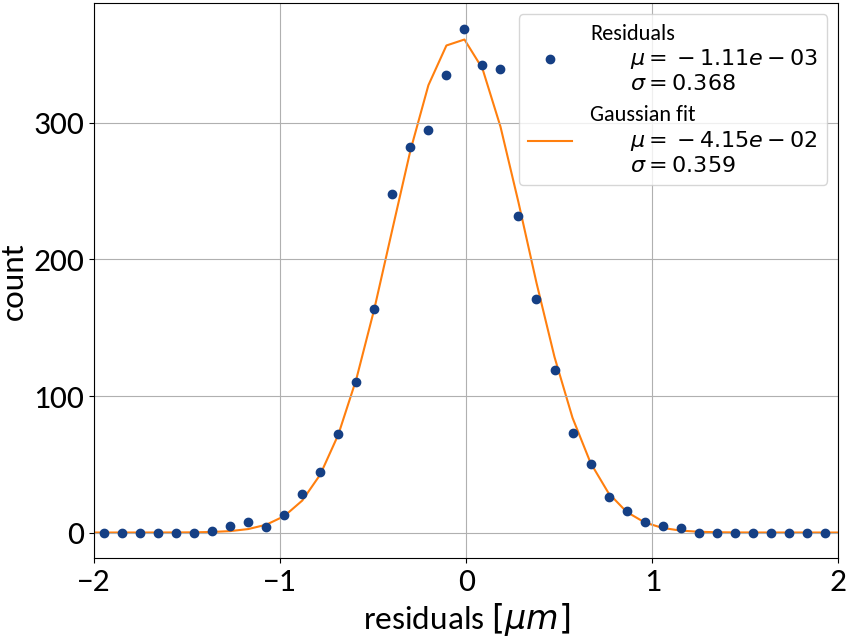
\begin{aligned} K &= \textrm{RBF} \\ \gamma &= 10^{-4} \\ \epsilon &= 10^{-8} \\ C &= 10^3 \end{aligned}
\mu m^2

Artificial Neural Networks

Inspired by the human brain, many "neurons" linked together

Input layer

Weights

Bias

Apply non-linearity, e.g. sigmoid, tanh

Perceptron

y(x) = \sigma\left( W\cdot x + b \right)

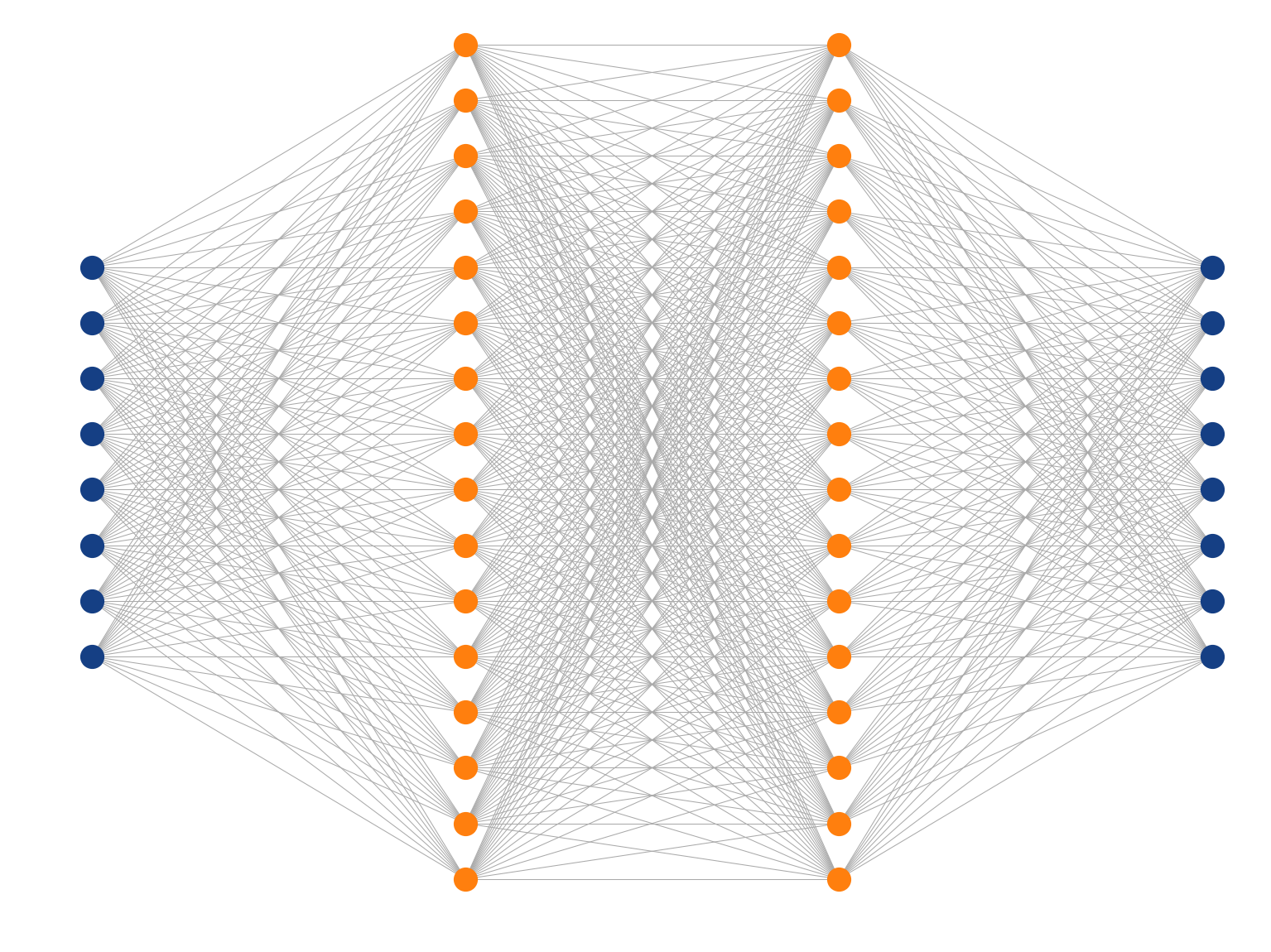
Multi-Layer Perceptron

Deep Learning

https://xkcd.com/1838/

What means deep?
Usually two or more hidden layers.

Using fully connected layers, the number of parameters can grow quite large (e.g. one of the MNIST top classifiers uses 6 layers = 11,972,510 parameters).

All those parameters are adjusted using the training data.

How deep networks learn

Define a loss function that assesses how good the network's predictions are, e.g. mean squared error:

L = \sum_i \left( y_i - \hat{y_i} \right)^2

Compute the gradient of the loss with respect to network parameters, e.g. Gradient Descent or Adam (uses "momentum").

w \rightarrow w - \eta\frac{\partial L}{\partial w}

Update the network's parameters by applying the gradient with a learning rate:

Deep Learning Frameworks

ANN Architecture

IDense = partial(Dense, kernel_initializer=VarianceScaling())

# Create feed-forward network.
model = Sequential()

# Since this is the first hidden layer we also need to specify
# the shape of the input data (49 predictors).
model.add(IDense(200, activation='relu', input_shape=(49,))
model.add(IDense(170, activation='relu'))
model.add(IDense(140, activation='relu'))
model.add(IDense(110, activation='relu'))

# The network's output (beam sigma). This uses linear activation.
model.add(IDense(1))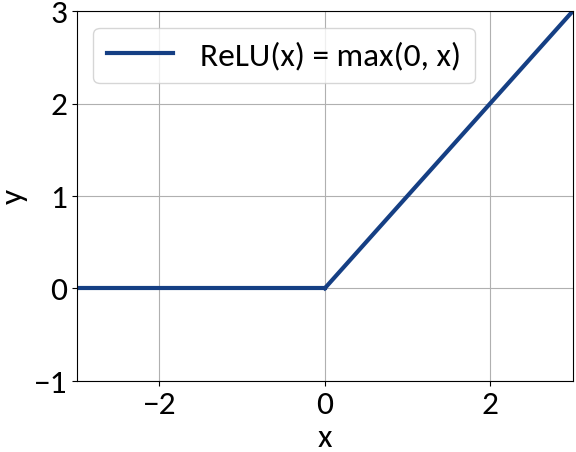

Activation function

Fully-connected (dense) feed-forward (sequential) architecture

ANN Learning

model.compile(
    optimizer=Adam(lr=0.001),
    loss='mean_squared_error'
)

model.fit(
    x_train, y_train,
    batch_size=8, epochs=100, shuffle=True,
    validation_data=(x_val, y_val)
)

D. Kingma and J. Ba, "Adam: A Method for Stochastic Optimization", arXiv:1412.6980, 2014

Other possible optimizers are Stochastic Gradient Descent for example.

Batch learning

  • Training is an iterative procedure
  • Need to go through the data set multiple times (= 1 epoch)
  • Weight updates are performed in batches (🡒 batch size)

After each epoch compute the loss on the validation data in order to prevent overfitting

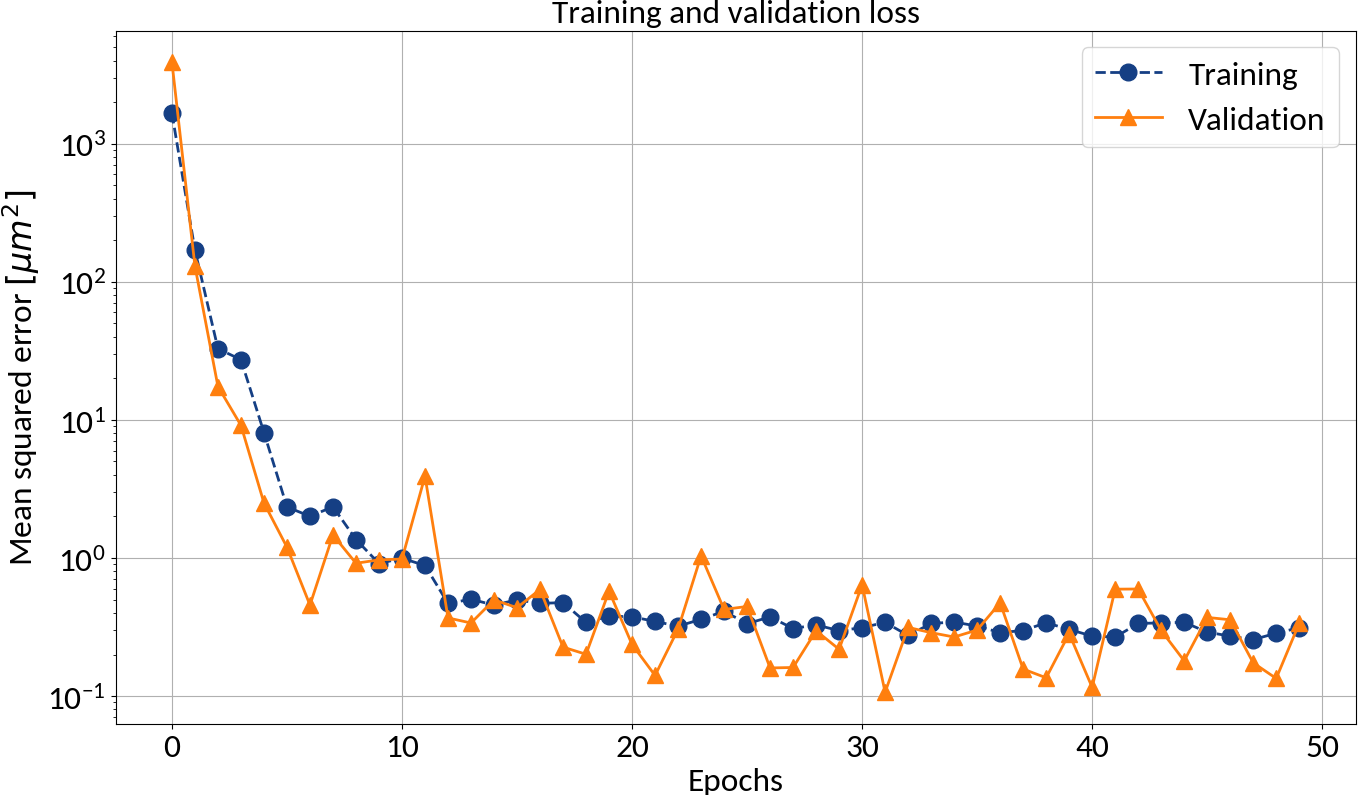
Could apply early stopping

ANN - Results

Explained variance 0.99988
R2-score 0.99988
Mean squared error 0.10959
\mu m^2

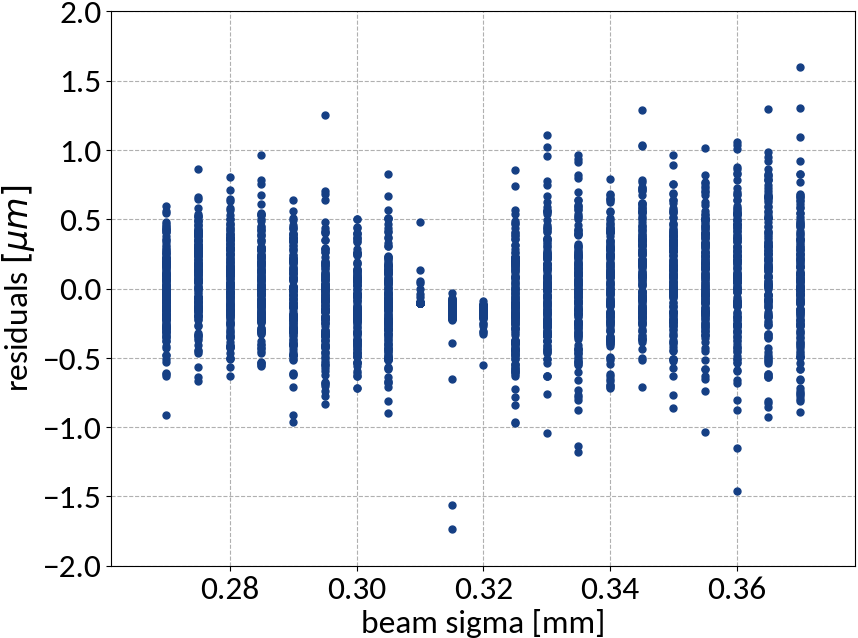
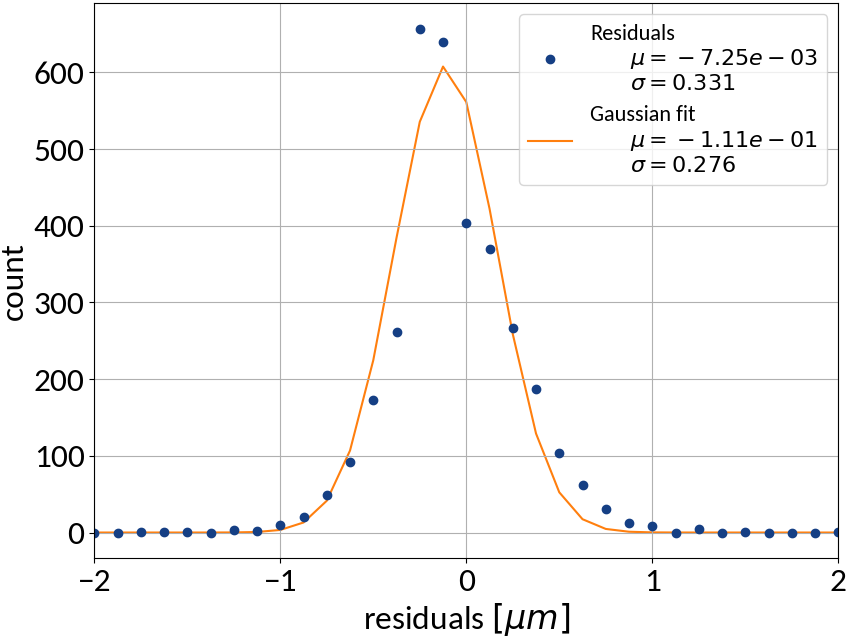
Summary of model performance

μ (res.) σ (res.) R2-score MSE
Linear 0.000213 0.502 0.99972 0.22512
KRR 0.00590 0.388 0.99983 0.15074
SVR -0.00111 0.368 0.99985 0.13527
ANN -0.00725 0.331 0.99988 0.10959

Values are given in units of

\mu m, \mu m^2 (\textrm{MSE}).
  • Artificial neural network (multi-layer perceptron) showed the best performance
  • Although the residuals changed with sigma, no bias occurred and beam sigma is expected to be in the center of the range anyway

Performance on test data

Explained variance 0.99988
R2-score 0.99988
Mean squared error 0.10815
\mu m^2

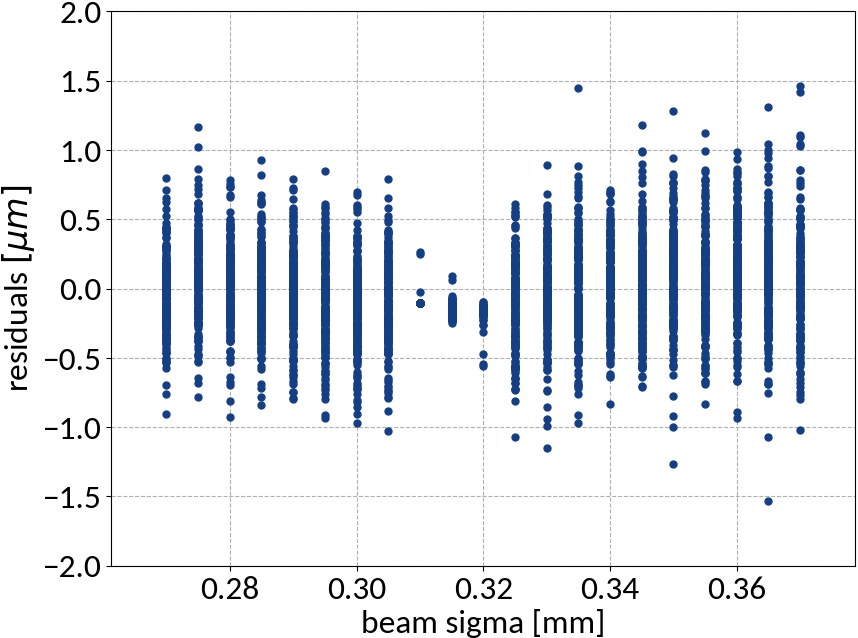
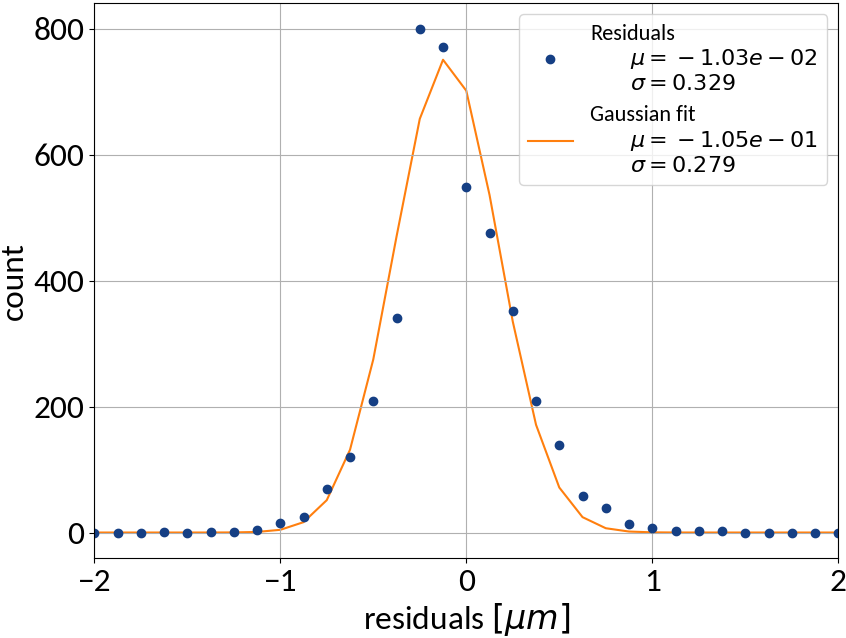
Using ANN

Measuring space-charge induced profile distortion

Measurements taken at CERN / SPS / BGI-H

Electric field 4 kV / 85 mm
Magnetic field 0.2 T (50A)

At the max. magnetic field no profile distortion occurs, but we can reduce the magnet current to make that happen

Acquisition system:

MCP + Phosphor + Camera

Protons
Energy 400 GeV
Bunch pop. 2.859e11
Beam width (1σ) 0.835 mm
Beam height (1σ) 0.451 mm
Bunch length (4σ) 1.6 ns

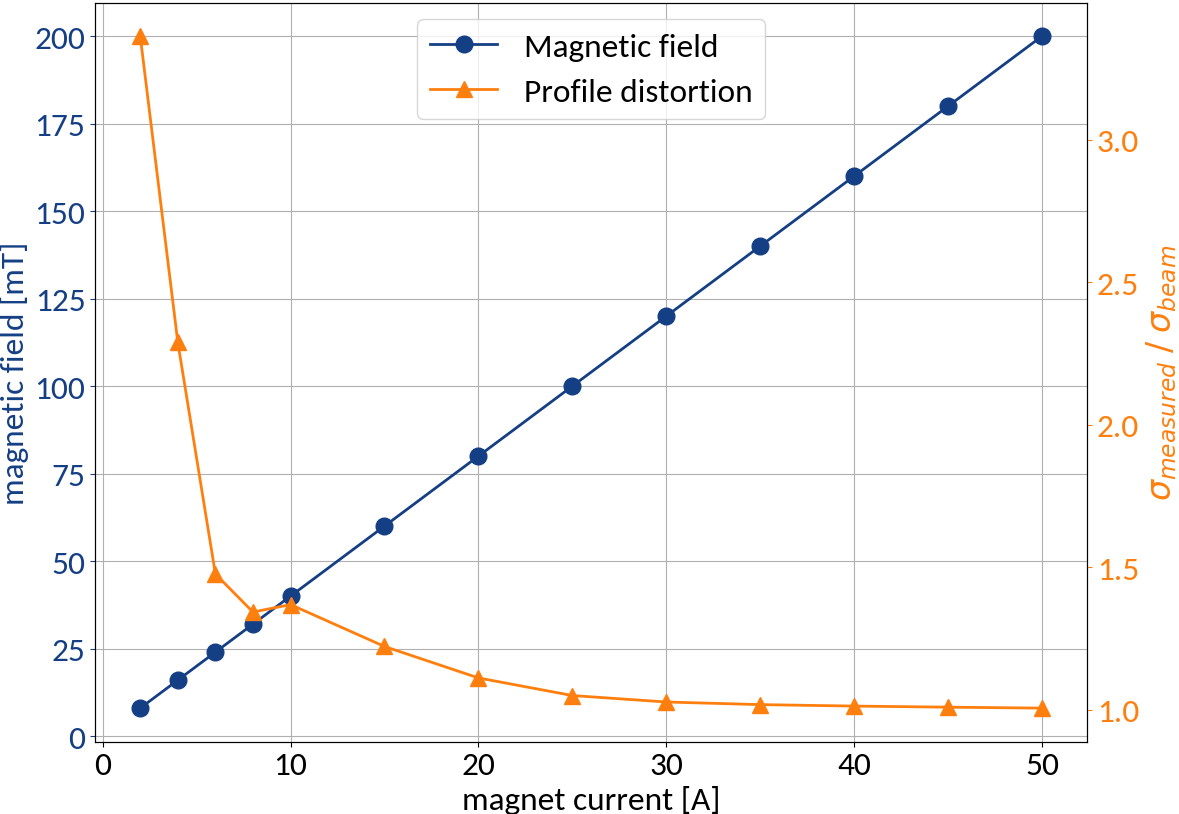
The Measurements

Taking into account:

  • Pixel-to-mm calibration
  • Camera rotation
  • Optical PSF (~ 130 μm)

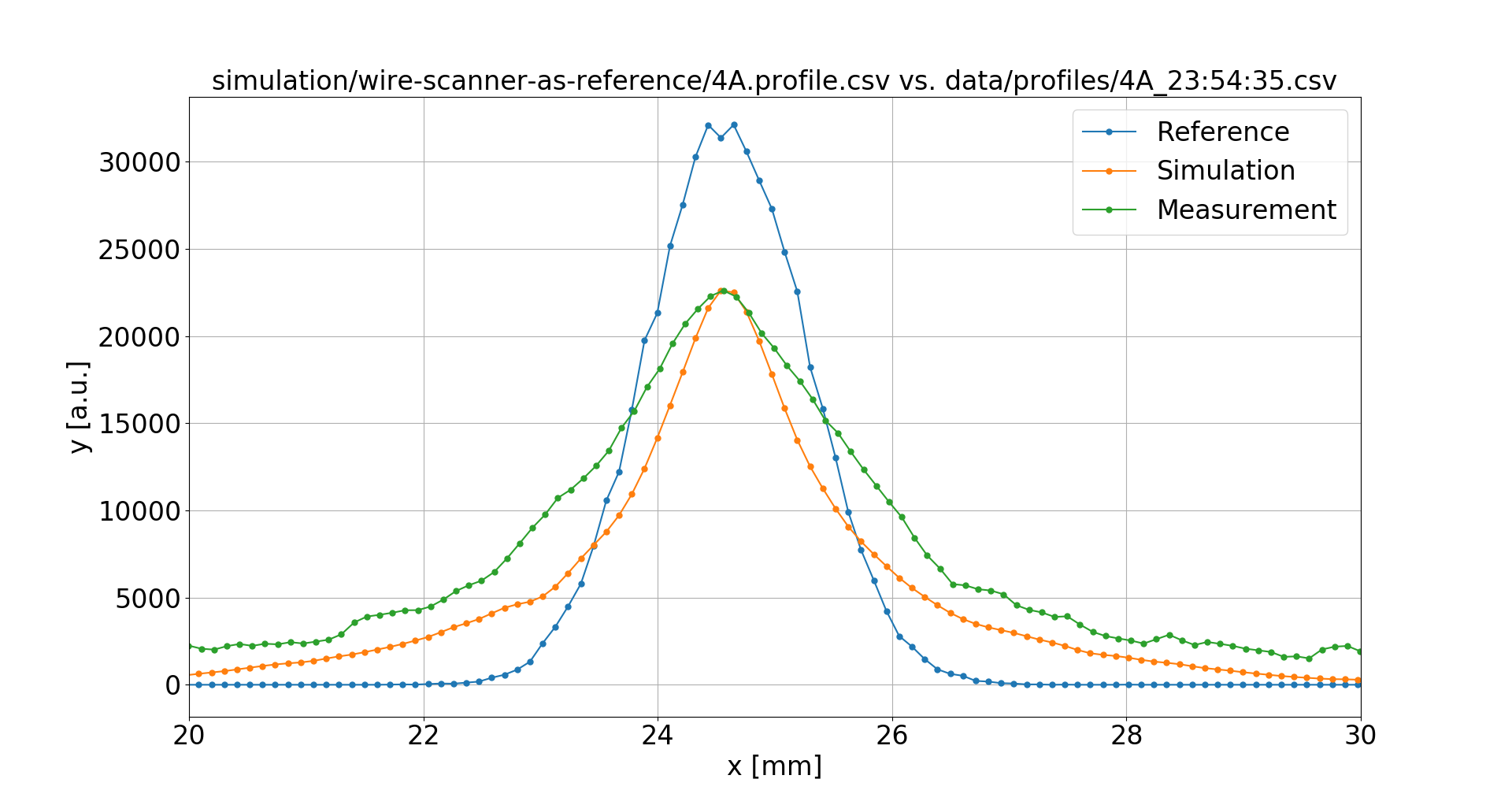
Wire Scanners were used to obtain undistorted reference profiles, however only the sigma values from fit were available

Bad luck with the RNG

4 A
16 mT

20 A
80 mT

What about the PSF?

Trying a 520 μm point-spread function instead:

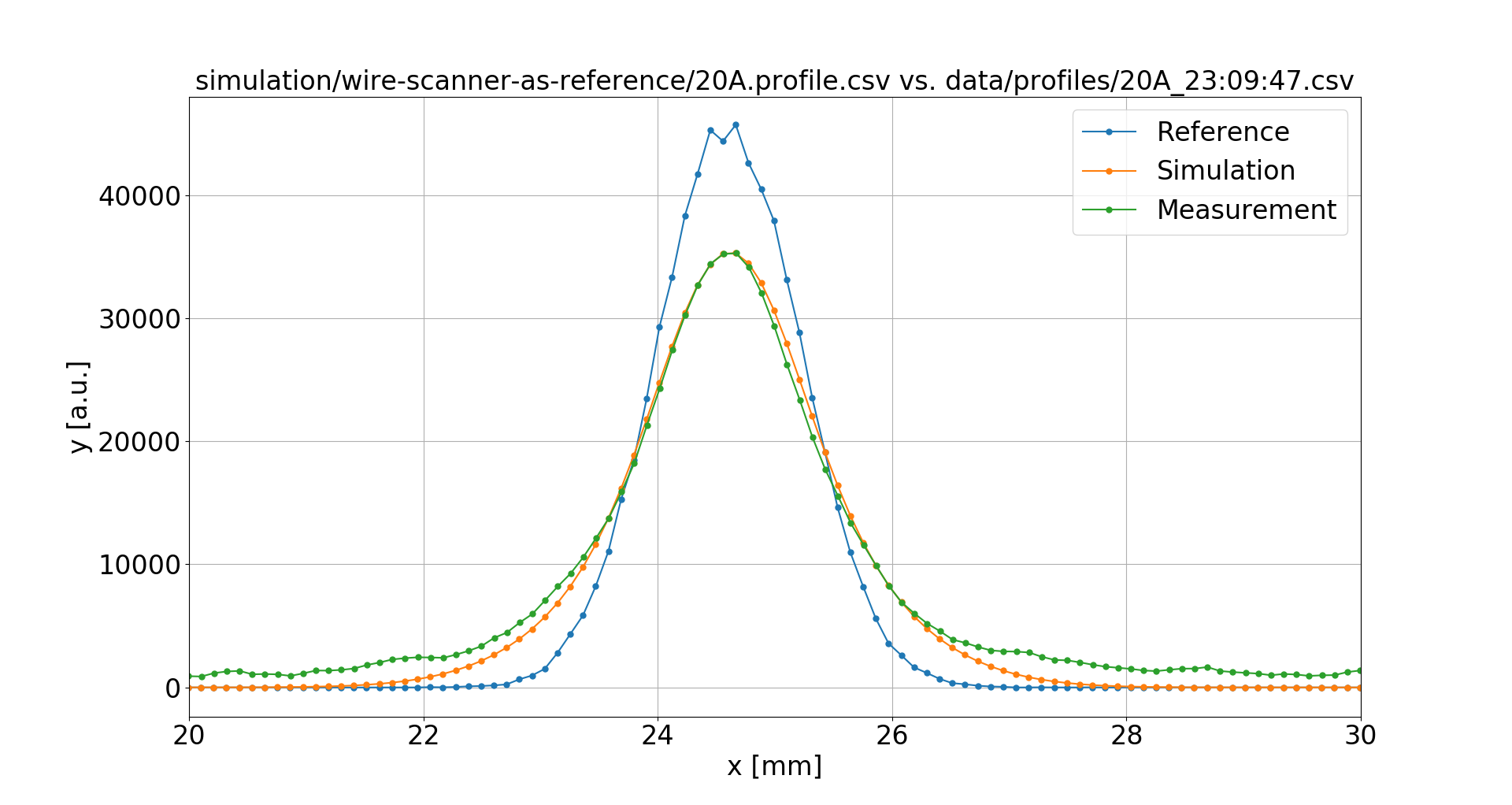
This resolves the deviations for all magnetic field values.

4 A
16 mT

20 A
80 mT

However such a large PSF is difficult to explain.

Next steps

Hyper-parameter tuning is tedious but there are helpful tools

Collect more data from measurements

Test the method against measured reference profiles (e.g. from Wire Scanners)

Test the method with "unclean" data (e.g. noise added, PSF applied)

from sklearn.model_selection \
    import GridSearchCV

from autosklearn.regression \
    import AutoSklearnRegressor

Investigate the effect of different profile binnings, i.e. different number of predictors

All models are wrong but some are useful.

- George Box (1978)

Piqued your interest?

Icons by icons8.

Please find more information at https://ipmsim.gitlab.io/IPMSim/

The data presented in this talk was generated with Virtual-IPM

https://gitlab.com/IPMsim/Virtual-IPM

https://pypi.org/project/virtual-ipm

Made with Slides.com