Keys
Addresses
Wallets
icons by TheNounProject
Photo by Vadim Sherbakov on Unsplash
Laurent Hardy
Photo from VitalCheck
Banking today
- Prove your identity
- Have enough money to start
- Trust the bank and government to handle your private information
- Pay for maintenance
- Wait for everything





ID
money
trust the bank
account + access

Let's do banking
Photo by Jingyi Wang on Unsplash
Bitcoin today
- Go online
- Generate a pair of keys

Let's do bitcoin



a private key – Available in different formats, must be kept private
an address – Used to receive payments, can be shown to anybody
example 1: 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy example 2: qR code

private key ≈ secret key ≈ sk

private key
address
How is a pair of keys enough?
Prove your private key is the owner of your public key
(sk,pk) := generateKeys(keysize)
Prove you own a public key without revealing the private key
sig := sign(message,sk)
Let everyone verify you own a public key without revealing the private key
isValid := verify(message,sig,pk)
private key ≈ secret key ≈ sk
public key ≈ pk
sig ≈ digital signature
Private Key
An private key is a 256-bit randomly generated number between
The total number of 256-bit numbers is equal to \(2^{256}\)
see why \(2^{256}\) is an astronomical number
source: Mastering Bitcoin, LearMeABitcoin
"epiclabs"
Binary:
1101111101011011011000101011111001111100111011011110100110010101001001010101000001010111110011111001010101011001100001101001100001010000101010111101011001110101010010010101010101110000100110001110010010000110111000111110100010111100100111010111000000011111
Decimal:
101027229823651685479805873605520737270124184003399402029102140131823486595103
Hexadecimal:
df5b62be7cede995255057cf9559869850abd67549557098e486e3e8bc9d701f
0 and 115792089237316195423570985008687907853269984665640564039457584007913129639935
Public Key
An public key is derived from the private key and is obtained through ECDSA (Elliptic Curve Digital Signature Algorithm).
- Start at G
- Draw a tangent
- Find the intersection (-2G)
- Take the inverse (2G)
This is one round of elliptic curve multiplication (i.e an elliptic curve multiplication of 2).
To find a public key, "multiply" G by the private key, i.e bounce around the ecliptic curve private key numbers of times.
source: Mastering Bitcoin, LearMeABitcoin
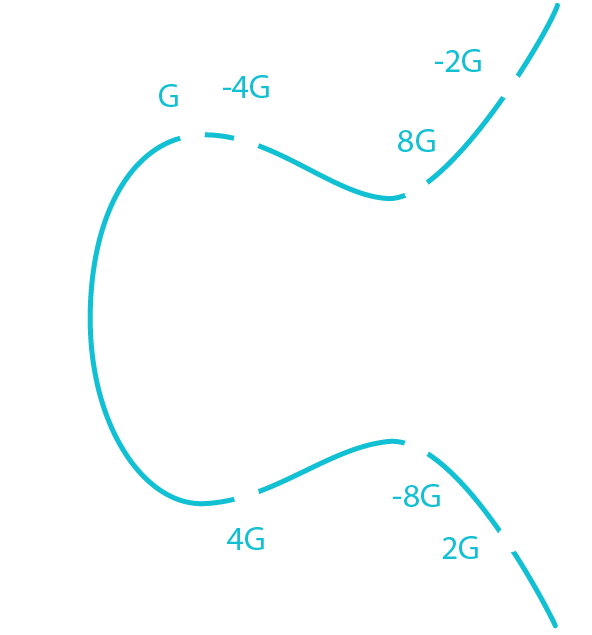
Public Key
Public Key = G * Private Key
Public Key = G * df5b62be7cede995255057cf9559869850abd67549557098e486e3e8bc9d701f
Through ECDSA we get 2 new coordinates:
x = 81591541406288143274758265124625798440200740391102527151086648448953253267255
y = 64573953342291915951744135406509773051817879333910826118626860448948679381492
In hexadecimal
Public Key (x) = b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737
Public Key (y) = 8ec38ff91d43e8c2092ebda601780485263da089465619e0358a5c1be7ac91f4
Keep only the (x) coordinate and discriminate the sign of the (y) coordinate
Public Key = 02b4632d08485ff1df2db55b9dafd23347d1c47a457072a1e87be26896549a8737
source: LearMeABitcoin
Address
An address is derived from the public key through the use of one-way cryptographic hashing (SHA256 and RIPEMD160).
Addresses are almost always presented to users in an encoding to help human readability, avoid ambiguity, and protect against errors (Base58Check).
Example: 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
source: Mastering Bitcoin
Wallet
A wallet is a software application that contain your private key, can generate pair of keys and make things convenient for the user.
Wallets contain keys, not coins! Wallets are keychains.
- Nondeterministic (Random) Wallets
- Deterministic (Seeded) Wallets
- Mnemonic Code Words
- Hierarchical Deterministic Wallets
source: Mastering Bitcoin
How is a pair of keys enough?
Prove your private key is the owner of your public key
(sk,pk) := generateKeys(keysize)
Prove you own a public key without revealing the private key
sig := sign(message,sk)
Let everyone verify you own a public key without revealing the private key
isValid := verify(message,sig,pk)
private key ≈ secret key ≈ sk
public key ≈ pk
sig ≈ digital signature
Digital Signature
Used to claim ownership of your bitcoin (UTXO).
A digital signature (Sig) is public information, accesible to everyone.
It is unique to the message, i.e the signature changes with the message being signed.
Ran = G * Random Number Sig = [Ran * Private Key] + Message / Random Number
Sig = [Ran * Private Key] + H[transaction] / Random Number
You can proof you own a public key by giving Ran and Sig to someone.
source: LearMeABitcoin
How is a pair of keys enough?
Prove your private key is the owner of your public key
(sk,pk) := generateKeys(keysize)
Prove you own a public key without revealing the private key
sig := sign(message,sk)
Let everyone verify you own a public key without revealing the private key
isValid := verify(message,sig,pk)
private key ≈ secret key ≈ sk
public key ≈ pk
sig ≈ digital signature
Verify a Signature
The goal is to verify that the public key and the digital signature were made using the same private key by giving them Sig, Ran, Private Key and Message.
Point 1 = G * [Sig * Message]
Point 2 = Public Key * [Sig * Ran]
Point 3 = Point 1 + Point 2
If Point 3 is equal to Ran then the signature has been proven to be valid
Ran = G * Random Number
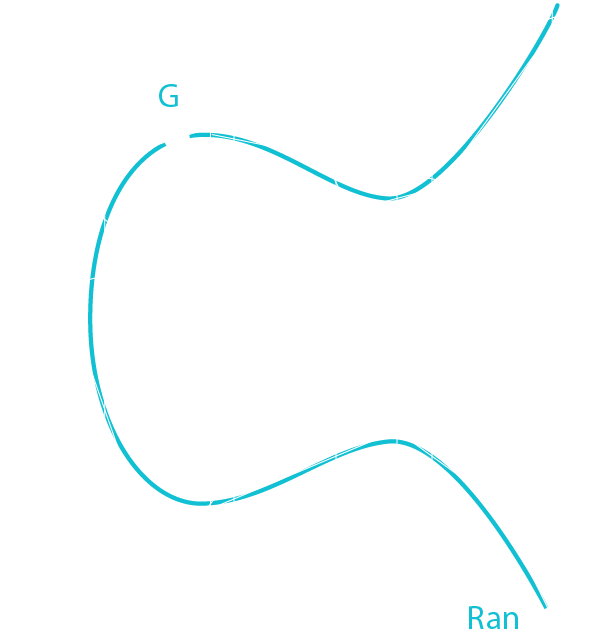
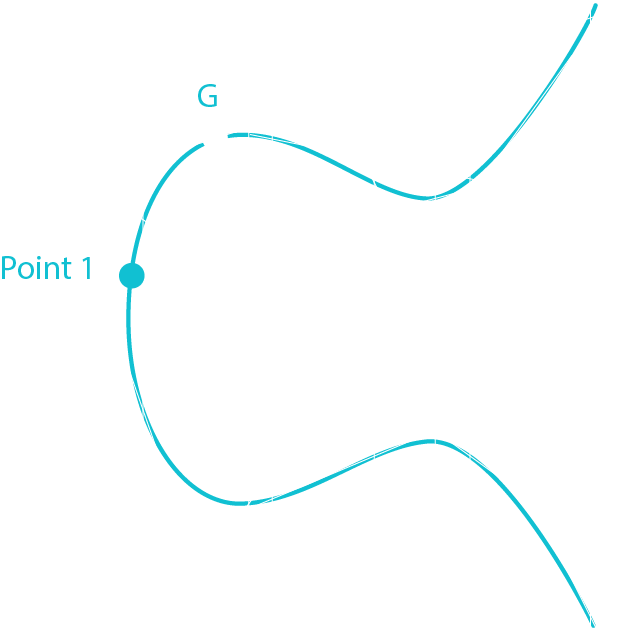
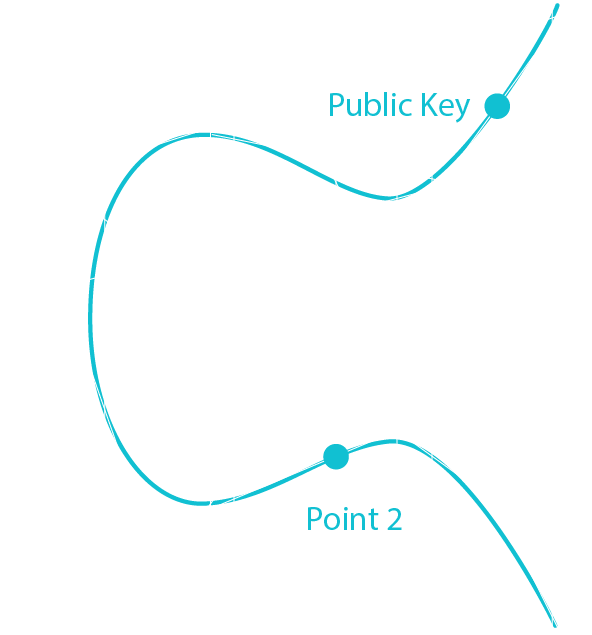
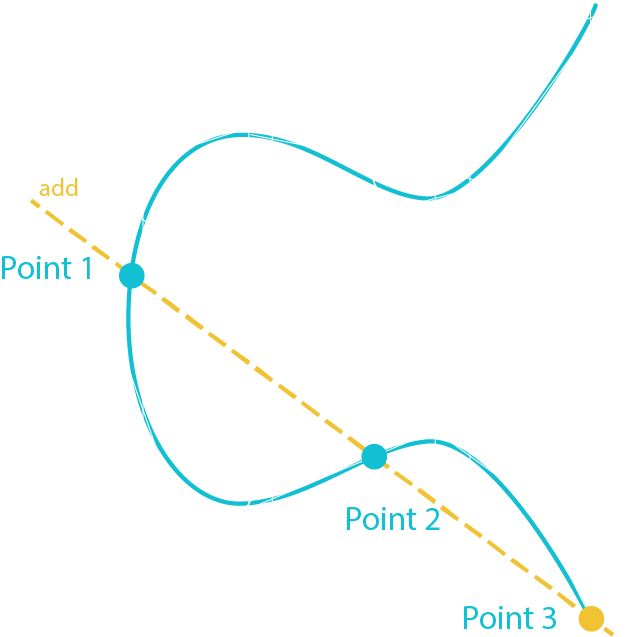
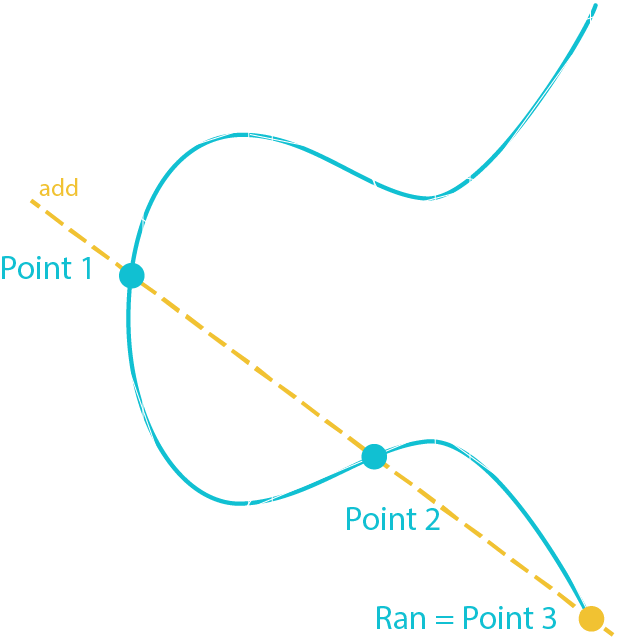
Photo by Karen Maes on Unsplash
Photo by Markus Spiske on Unsplash
Storing crypto assets
| availability |
| security |
| convenience |
be able spend your coin whenever you want
make sure nobody else can spend your coin
managing your keys in a relatively easy way
local storage


cold storage
app wallets


paper wallets
hierarchical deterministic wallets
hardware wallets
air gapped computer
hot storage
hot side
cold side
hierarchical deterministic wallets
generate keys function
private key generation info
address generation info
generate address
generate key
\(i\) th address
\(i\) th
key
\(i\)
\(i\)
hardware wallets


Ledger Nano S [LedgerWallet]
Trezor [SatoshiLabs]
Photo by Karen Maes on Unsplash



