Debug Machine learning embedded SQL
ML-Embedded SQL

How many cats in the picture?
ML-Embedded SQL

How many cats in the picture?



{Cat,Cat,Cat,Dog,Dog,Dog,Dog,...}






Count(Cat) = 3
SELECT COUNT(*)
FROM image
WHERE classify(patch) == "cat"
ML-Embedded SQL




{Cat,Cat,Cat,Dog,Dog,Dog,Dog,...}






Count(Cat) = 3
More practically
ML-Embedded SQL
ML-Embedded SQL important because:
- Machine learning is put into use as a system but not standalone
- Given the data size is large, we want to move computation to the data rather than move data to the computation
- Big companies are using!



ML-Embedded SQL
How many cats in the picture?
WRONG




{Cat,Cat,Cat,Dog,Dog,Dog,Dog,...}






Count(Cat) = 3
ML-Embedded SQL
Goal: Why & How
ML-Embedded SQL




- Column: Feature-based
ML Interpretations
- Row: Case-based
* Masked due to the actual knowledge is encoded into the model by learning


ML-Embedded SQL
- Column: Predicate-based
SQL Interpretations
- Row: Provenance-based
\(\rho_{B=1}\): Caused the issue
| a | b | c |
| d | b | e |
| A | B | C |
|---|---|---|
| a | b | c |
| d | b | e |
| f | g | e |
| A | B | C |
ML-Embedded SQL
Predicate-based > Feature-based
* Cased-based = Provenance based
ML-Embedded SQL
Causality model: counterfactual
\(A \rightarrow B\)
If not A then not B
-- In the absence of a cause, the effect doesn’t occur
In database
Given a query \(Q\), database \(D\), \(t \in D\) is the cause of \(Q(D)\)'s incorrectness if \(Q(D-t)\) is correct.
ML-Embedded SQL
Combining SQL & ML interpretations?
- SQL with multiple models, how to reason between them?
- Error propagates, how to identify?
- Aggregate query shields provenance, how to penetrate?
- The query is complex, how to efficiently compute?
ML-Embedded SQL
- Problem Definition
- Solution
- Experiment
ML-Embedded SQL
\(D\): Database, \(D_T\): Database trains the models
\(Q\): Query
\(M_1,...,M_k\): Models
\(E\): User expectation of \(Q(D)\)
Goal: find tuples \(T \subset D_T\) causes \(Q(D) \neq E \)
ML-Embedded SQL
Counterfactual: find \(T \subset D_T\) that \(Q(D, D_T-T)= E\).
Trivial approach:
1. Pick up n tuples \(t \in D_T\) randomly, delete them.
2. Re-train all the models \(M_1,...,M_k\).
3. Run \(Q(D, D_T-T)\) to see if \(Q(D, D_T-T) = E\)
ML-Embedded SQL
Be smarter? Optimization!
Objective: Find a \(T\), if multiple solutions exist, we want the one with minimal \(|T|\)
Constraints:
1. The query result is correct \(Q(D, D_T-T)=E\)
2. The model should be well trained.
ML-Embedded SQL
Difficulties:
1. Encoding SQL logic into an analytical form
2. Efficiently solve the problem
Provenance Semirings
\(Q(D,D_T-T)\) is not analytical representable!
Provenance Semirings
| A | B | C |
|---|---|---|
| a | b | c |
| d | b | e |
| f | g | e |
SELECT *
FROM D
WHERE B = 'b'
| A | B | C |
|---|---|---|
| a | b | c |
| d | b | e |
How to express this analytically?
Provenance Semirings
Key idea: the SQL operators are actually set operations, so SQL should be isomorphic with some semirings
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 1 |
SELECT *
FROM D
WHERE B = 'b'
Where B = 'b' \(\rightarrow\) P(t) = 1{t.B = 'b'}\)
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 0 |
Provenance(t) = \(t.I \cdot P(t)\)
Provenance Semirings
Selection
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 1 |
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 1 |
Provenance(t) = \(t.I^1 +t.I^2\)
Provenance Semirings
Union
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
\(\bigcup\)
\(=\)
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 1 |
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 0 |
| f | g | e | 0 |
Provenance(t) = \(t.I^1 \cdot t.I^2\)
Provenance Semirings
Natual join
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
\(\bowtie\)
\(=\)
| A | B | C | I |
|---|---|---|---|
| a | b | c | 1 |
| d | b | e | 1 |
| f | g | e | 1 |
| B | V | I |
|---|---|---|
| b | 2 | 1 |
| g | 1 | 1 |
Provenance(t) = \(t.I \cdot P(t)\)
Provenance Semirings
Aggregation
\(\gamma_B, count\)
\(=\)
Provenance_count(t) = \(\sum t.I \cdot P(t) \cdot 1\)
Provenance Semirings
\(Q(D,D_T-T) \xrightarrow{semiring} Q_a(D,D_T-T)\)
Efficiently solve the problem
Gradient descent with Tensorflow
1. Relax integers (from provenance) to continuous variable
2. Relax constraints into objective
3. Using KKT condition to remove the sub-level optimization
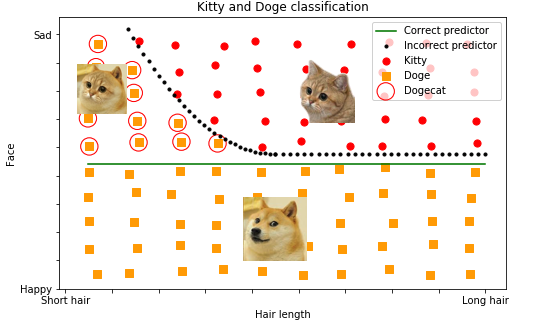
A preliminary result
SELECT Count(*) FROM D WHERE classify(P) = 'dog'
Too much!!
Further works
1. Gradient approach is still slow: A better algorithm to approximate objective
2. Provenance semiring is a complete solution. However, given some special types of queries, a simplified problem formulation may exist (i.e. predicate push down to avoid quadratic joins)
Conclusion
ML/SQL explanation still have lots of opportunies
1. Standardize/solid foundation
2. More ways to do explanation (Row, Column, Row/Column)
3. More efficient/accurate explanation