Enabling SQL-ML Explanation to Debug
Training Data
Weiyuan Wu
youngw@sfu.ca
Committee:
Dr. Jiannan Wang - Senior Supervisor
Dr. Jian Pei - Supervisor
Dr. Oliver Schulte - Examiner
Dr. Steven Bergner - Chair
Thesis Defense
Aug. 22. 2019
SQL-ML Query
SELECT COUNT(*)
FROM INBOX
WHERE predict(INBOX.text) = 'spam'
AND INBOX.date = 'Aug. 22, 2019'SQL-ML System



Why SQL-ML System
- Democratize AI
- Improve Productivity
- Facilitate Management
Training Data is Often Corrupted

| ID | Text | Label |
|---|---|---|
| 1 | CLICK AND GET FREE PICKLE AT http://spam.com/clickme... | Spam |
| 2 | Hi Rick, lets have a meeting tmr 8pm -Rick | Spam |
| 3 | Grandpa, the light in the garage is broken - Morty | Ham |
| Spam |
Corrupted training data
The Need for SQL-ML Explanation
SELECT COUNT(*)
FROM INBOX
WHERE predict(INBOX.text) = 'spam'
AND INBOX.date = 'Aug. 22, 2019'Why is it so high?
| Count(*) |
|---|
| 1000 |
A Debugging Workflow
| ID | Text | Label |
|---|---|---|
| 1 | CLICK AND GET FREE PICKLE AT http://spam.com/clickme... | Spam |
| 2 | Hi Rick, lets have a meeting tmr 8pm -Rick | |
| 3 | Grandpa, the light in the garage is broken -Morty | Ham |

Why is it so high?

2. A SQL-ML Explanation tool
3. Training set bugs
1. A complaint
- Software debugging:
assert query(DB) <= 20Spam
Existing Approches
- SQL Explanation
- Why Not? [A Chapman et al. SIGMOD'09]
- Tiresias [A Meliou et al. SIGMOD'12]
- Scorpion [E Wu et al. VLDB'13]
- ML Explanation
- Influence Function [PW Koh et al. ICML'17]
- DUTI [X Zhang et al. AAAI'18]
SQL & ML Explanation
SELECT COUNT(*)
FROM INBOX
WHERE predict(INBOX.text) = 'spam' Too High!
Training data
Predictions
Count(*)
Querying data
Model
SQL Explanation
ML Explanation
Complaint
Labels
Training Set Bugs
\(\Bigg\}\)
\(\Bigg\}\)
Simple Combination
- SQL explanation: produces labels for querying set
- ML explanation: requires labels for querying set to debug
- HowToComp:
SQL Exp.
ML Exp.
Querying Set Points
Possible Corruptions
Ambiguity
SQL Exp.
ML Exp.
Querying Set Points
Possible Corruptions
- HowToComp: Multiple ways to select querying set points.

Agenda
- Motivation & Background
- Problem Definition & Challenges
- Our Solution
- Experiments
- Conclusions
The SQL-ML Explanation Problem
Inputs:
- A training dataset
- A SQL-ML query
- A complaint (e.g. count is too high)
Output:
- Possible corrupted training data points
\(\checkmark\) Provenance Polynomial
\(\checkmark\) Relax and Combine
\(\checkmark\) Influence Function
Challenges
- Problem Formulation
- Holistic
- Discrete + Continous Optimization
- Efficient Algorithm
- Need to train \(n^k\) models
Agenda
- Motivation & Background
- Problem Definition & Challenges
- Our Solution
- Experiments
- Conclusions
InfComp: Influence & Complaint
-
Compute influence on the differentiable query result
- Make SQL query result differentiable w.r.t. model parameters by provenance polynomial
- Training set debug using Influence Function
Differentiable Query Result
SELECT COUNT(*)
FROM INBOX
WHERE predict(INBOX.text) = 'spam' COUNT(*): \(\mathcal{Q} = f(P1,P2,P3) = P1 + P2 + P3\)
where \(P1,P2,P3 \in \{0,1\}\)
| ID | Text | Predicted |
|---|---|---|
| 1 | WANTED: Rick, for crime against interdimensional space | |
| 2 | Hi Rick, lets reschedule the meeting to next Monday -Rick | |
| 3 | http://test-spam.com... |
| ID | Text | Predicted |
|---|---|---|
| 1 | WANTED: Rick, for crime against interdimensional space | P1 |
| 2 | Hi Rick, lets reschedule the meeting to next Monday -Rick | P2 |
| 3 | http://test-spam.com... | P3 |
SQL Provenance
- SQL operators are isomorphic to some semimodules
- \(\pi, \sigma, \gamma, \bowtie, \cup\) can be expressed using a boolean semimodule or integer semimodule, depending on the set or bag semantics
- Example:
| A | B | P |
|---|---|---|
| a | b | 1 |
| d | b | 1 |
| f | g | 1 |
| A | B | P |
|---|---|---|
| a | b | 1 |
| d | b | 0 |
| f | g | 0 |
Provenance(t) = \(t.P^1 \cdot t.P^2\)
| A | B | P |
|---|---|---|
| a | b | 1 |
\(\bowtie\)
\(=\)
Table 1
Table 2
| d | b | 0 |
| f | g | 0 |
Connect ML and SQL
-
Issue: Non-differentiable
- \(f(P1,P2,P3) = P1 + P2 + P3\)
- \(P1,P2,P3 \in \{0,1\}\)
- Solution: Relaxation
- Relax binaries into continuous: \(P1',P2',P3' \in [0,1]\), thus \(f(P1',P2',P3') \in [0,3]\)
- Replace \(P1', P2', P3'\) with the probabilistic output from the model
- Now the query output \(\mathcal{Q}\) is differentiable w.r.t. ML params!
Training Set Debugging
| ID | Text | Label |
|---|---|---|
| 1 | CLICK AND GET FREE PICKLE AT http://spam.com/clickme... | Spam |
|
|
||
| 3 | Grandpa, the light in the garage is broken - Morty | Ham |
| 2 | Hi Rick, lets have a meeting tmr 8pm -Rick | Spam |
Training data
Count(*)
......
Influence
Training data
Model Params
Influence
Function\(^1\)
How?
Count(*)
Chain Rule
[1]: PW Koh et al. ICML'17
Influence Function
Where:
\(\theta^* = \argmin_{\theta} L(\theta)\)
\(L(\theta) = \sum_{(x,y) \in T} \ell( f(x, \theta),y) \)
\(\theta_{\epsilon}^* = \argmin_{\theta} L(\theta) + \epsilon \cdot \ell( f(x', \theta),y')\)
\(H_{\theta} = \nabla_{\theta}^2 L(\theta) \)
- Influence Function: \[\left. \frac{d \theta_{\epsilon}^*}{d\epsilon}\right|_{\epsilon=0} = \lim_{\epsilon \to 0} \frac{\theta_{\epsilon}^* - \theta^*}{\epsilon} = - H_{\theta^*}^{-1} \nabla_{\theta^*} \ell( f(x', \theta^*),y') \]
- InfComp: \[ \left. \frac{d q(\theta_{\epsilon}^*) }{d\epsilon}\right|_{{\epsilon=0}} = - \nabla_{\theta} q(\theta^*) \left. \frac{d \theta_{\epsilon}^*}{d\epsilon}\right|_{\epsilon=0} = - \nabla_{\theta} q(\theta^*) \ H_{\theta^*}^{-1} \ \nabla_{\theta} \ell( f(x', \theta^*),y') \]
InfComp Algorithm


K most possible corruptions
2. Relax and plug in models
1. Expression of the query result using provenance
3. Calculate the influence
5. Delete the most influential training point and re-train
4. Rank the training points by the influence
Until K points deleted
Agenda
- Motivation & Background
- Problem Definition & Challenges
- Our Solution
- Experiments
- Conclusions
Experiment: Compared Methods
[1]: PW Koh et al. ICML'17
[2]: A Meliou et al. SIGMOD'12
- Baselines:
- Complaint agnostic:
- Loss: delete training points with maximum loss values
- InfLoss\(^1\): delete training points with maximum self-influences
- Complaint aware:
- HowToComp\(^{1,2}\): delete training points by first using SQL explanation tools and then Influence Function
- Complaint agnostic:
- Our approach:
- InfComp: Complaint aware, deleting training points by holistically considering SQL and ML
Experiment: Tasks
- Entity resolution task: DBLP-GOOG dataset
- Image recognition task: MNIST dataset
- Spam classification task: ENRON dataset

SELECT COUNT(*)
FROM DBLP, GOOG
WHERE predict(DBLP.*,GOOG.*) = true
SELECT COUNT(*)
FROM L, R
WHERE predict(L.img) = predict(R.img)SELECT COUNT(*) FROM INBOX
WHERE INBOX.text LIKE ’%special_word%’
AND predict(INBOX.text) = ’spam’dear partner ,
we are a team of government officials that belong to an eight - man committee in the ...
...
sincerely ,
john adams
( chairman senate committee on banks and currency )
call number : 234 - 802 - 306 - 8507



L:
R:

GOOG:
DBLP:
Corruptions
- Random Label Flip: DBLP/MNIST
- Positive/Negative Label Flip: DBLP/MNIST
- Label Generation from a corrupted labeler: MNIST
- Label Flip by word: ENRON
Experiment Results: MNIST
The Top K Corrutption Recall on MNIST. The closer to the ground truth line, the better.
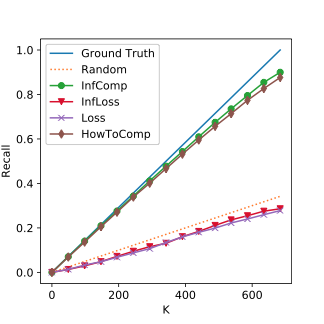
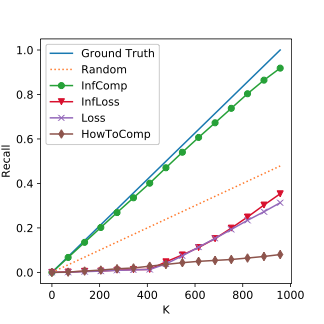
SQL Exp.
ML Exp.
Querying Set Points
Possible Corruptions
Ambiguity!
Median Corruption
High Corruption
Corruption overwhelms!
Experiment Results: DBLP & ENRON
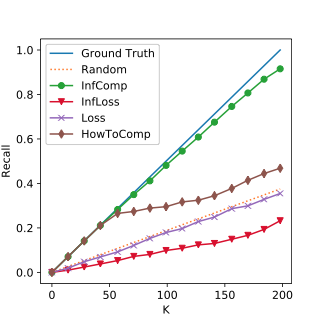
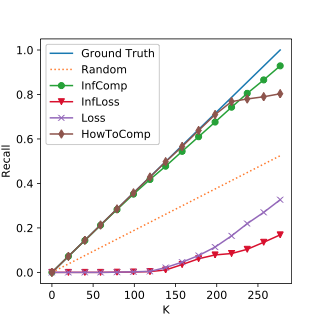
The Top K Corrutption Recall on DBLP. The closer to the ground truth line, the better.
Median Corruption
High Corruption
The Top K Corrutption Recall on ENRON. The closer to the ground truth line, the better.
"deal" Corruption
"http" Corruption
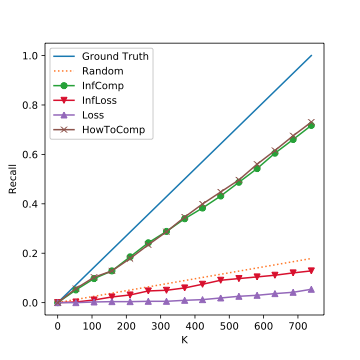
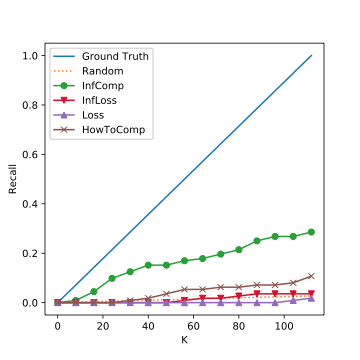
Experiment Result: Time Overhead
Average time for finding one possible corruption, the lower the better. Loss: 1x, InfLoss: 2.4x, InfComp: 1.3x, HowToComp: 2x.
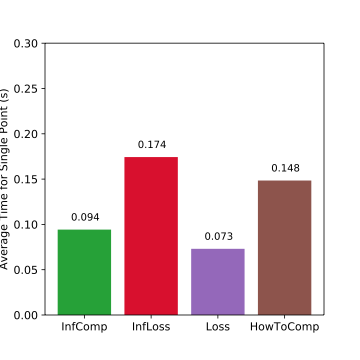
Conclusions
- To our best knowledge, InfComp is the first to debug SQL-ML query.
- Infcomp can leverage the complaint to find more corrupted training points compared to the baselines.
- InfComp is fast and adds little time overhead.
Future Works
- Richer set of explanations
- Integration to analytical databases
- Why not complaints