In Search of an Entity Resolution OASIS: Optimal Asymptotic Sequential Importance Sampling
Outline
- What's the goal
- Problem Definition
- OASIS: the algorithm
- Solve OASIS problem
- Experiments
Goal: Evaluate ER
Why Challenging?
- No ground truth.
- Imbalanced data:
- Uniformly sampling? no way!
- Ask Oracle? Money, hmmm.
- Blocking rules? Bias!
Problem Definition
1. Metric
It is reasonable to use F-measure as the evaluation metric.
\(TP = \sum^T_{t=1}\ell_t\hat{\ell}_t\),
\(FP=\sum^T_{t=1}(1-\ell_t)\hat{\ell}_t\),
\(FN=\sum^T_{t=1}\ell_t(1-\hat{\ell}_t)\).
\(\ell_t\): true label for pair \(t\).
\(\hat{\ell}_t\): estimated label for pair \(t\).
Where:
\(TP = \sum^T_{t=1}\ell_t\hat{\ell}_t\),
\(FP=\sum^T_{t=1}(1-\ell_t)\hat{\ell}_t\),
\(FN=\sum^T_{t=1}\ell_t(1-\hat{\ell}_t)\).
\(\ell_t\): true label for pair \(t\).
\(\hat{\ell}_t\): estimated label for pair \(t\).
Where:
\(\alpha = 0\): recall,
\(\alpha = 1\): precision.
2. Formulation
- Two data source: \(\mathcal{D}_1\) and \(\mathcal{D}_2\),
- Candidate pairs: \(\mathcal{Z} = \mathcal{D}_1 \times \mathcal{D}_2\),
- A similarity function: \(s: \mathcal{Z} \rightarrow \mathbb{R}\),
- Randomized Oracle: \(Oracle(z): \mathcal{Z} \rightarrow \{0,1\}\).
- An estimation \(\{\hat{\ell}_1, \hat{\ell}_2,...\}\).
- Approximate \(\mathit{F}_{\alpha,T}\)
- Minimize # Oracle query.
- Ground truth \(\{\ell_1,\ell_2,...\}\).
- Enough money.
Goal:
We have:
We don't have:
3. Good estimation
- Consistency: \(\hat{F}_\alpha \to F_\alpha\), where \(F_\alpha = \lim_{T \to \infty} F_{\alpha,T} \)
- Minimal variance: The variance of estimation should be minimized
4. Approach
With the purpose of getting \(F_\alpha\), sampling pairs and asking Oracle to estimate is a good choice.
Wait...
Wait...
Since the original distribution is imbalanced, uniformly sampling doesn't work here because of how we calculate \(F_\alpha\) (Why?).
Wait...
Since the original distribution is imbalanced, uniformly sampling doesn't work here because of how we calculate \(F_\alpha\) (Why?).
Wrong answers don't contribute to F score!
Biased sampling
So, why not use bias against bias?
Instead of sampling directly on \(p(x)\) to estimate \(\theta = E[f(X)] \),
i.e. \(\hat{\theta} = \frac{1}{T}\sum^T_{i=1}f(x_i)\),
we draw samples from \(q(x)\).
Interestingly, we can still do estimation by \(\hat{\theta}^{IS} = \frac{1}{T}\sum^T_{i=1}\frac{p(x_i)}{q(x_i)}f(x_i)\).
Biased sampling
OASIS
With the help of biased sampling:
Rewrite \(\textit{F}_{\alpha,T} = \frac{TP}{\alpha(TP+FP) + (1-\alpha)(TP+FN)}\)
to \(\textit{F}_{\alpha}^{AIS} = \frac{\sum^T_{t=1} w_t \ell_t \hat{\ell}_t}{\alpha \sum^T_{t=1}w_t\hat{\ell}_t + (1-\alpha)\sum^T_{t=1}w_t \ell_t}\)
Note:
With the help of biased sampling:
Rewrite \(\textit{F}_{\alpha,T} = \frac{TP}{\alpha(TP+FP) + (1-\alpha)(TP+FN)}\)
to \(\textit{F}_{\alpha}^{AIS} = \frac{\sum^T_{t=1} w_t \ell_t \hat{\ell}_t}{\alpha \sum^T_{t=1}w_t\hat{\ell}_t + (1-\alpha)\sum^T_{t=1}w_t \ell_t}\)
Find \(q(z_t)\), how?
Note:
Considering minimal variance
\(q^* \in \arg \min_q Var(\hat{F}_\alpha^{AIS}[q])\)
Previous work: \(q^*(z) \propto p(z) \cdot A(F_\alpha,p_{Oracle}(1|z_t))\)
\(w_t = \frac{p(z_t)}{q(z_t)}\)
Note: \(A(\cdot)\) here stands for ellipsis
Considering minimal variance
\(q^* \in \arg \min_q Var(\hat{F}_\alpha^{AIS}[q])\)
\(w_t = \frac{p(z_t)}{q(z_t)}\)
Note: \(A(\cdot)\) here stands for ellipsis
As long as we got \(F_\alpha\) and \(p_{Oracle}(1|z_t)\), problem solved.
Previous work: \(q^*(z) \propto p(z) \cdot A(F_\alpha,p_{Oracle}(1|z_t))\)
Considering consistency
\(q(z) = \epsilon \cdot p(z) + (1-\epsilon) \cdot q^*(z)\).
Epsilon greedy, multi-armed bandits problem.



Solve OASIS Problem
1. An iterative way
\(F_\alpha\) and \(p(1|z)\) - unknown!
Approximate them iteratively: For each step \(t+1\), use \(F_\alpha\) and \(p(1|z)\) in step \(t\).
2. \(F_\alpha\) - Simple
Intuitively, we can just use \(\hat{F}^{AIS}_\alpha\) instead of \(F_\alpha\).
3. \(p(1|z)\) - Big problem
There's no way we can do to get the distribution of the oracle without asking them for every \(z\).
But...
3. \(p(1|z)\) - Big problem
There's no way we can do to get the distribution of the oracle without asking them for every \(z\).
But...
Use stratification to approximate is feasible
Stratification
Stratification is a statistical method to estimate some variable by putting samples into several strata. A.K.A. bin boxes.
Stratification
Similarity func \(s: \mathcal{Z} \to \mathbb{R}\) kicks in.

For each \(z\) in \(P_k\), we can use \(p(1|P_k)\) instead of \(p(1|z)\) now.
We treat each \(p(1|P_k) \sim Bernoulli(\pi_k)\), so \(\pi_k \sim Beta(\alpha, \beta)\).
Stratification
How to update \(\alpha\) and \(\beta\) iteratively? Easy.
if \(\ell_t = 1\), \(\alpha += 1\)
if \(\ell_t = 0\), \(\beta += 1\)
Now we get \(F_\alpha\) and \(p(1|z)\)
Experiments
Settings:
- ER algorithm: Linear SVM
- Dataset: Products, restaurant, dblp, abt-buy, core, tweets100k
- Baselines:
- uniformly sampling,
- stratified uniform sample
- non-adaptive importance sampling


OASIS beats any other algorithms in these datasets

On balanced datasets, they behaviour similar



Choice of similarity func for IS is important
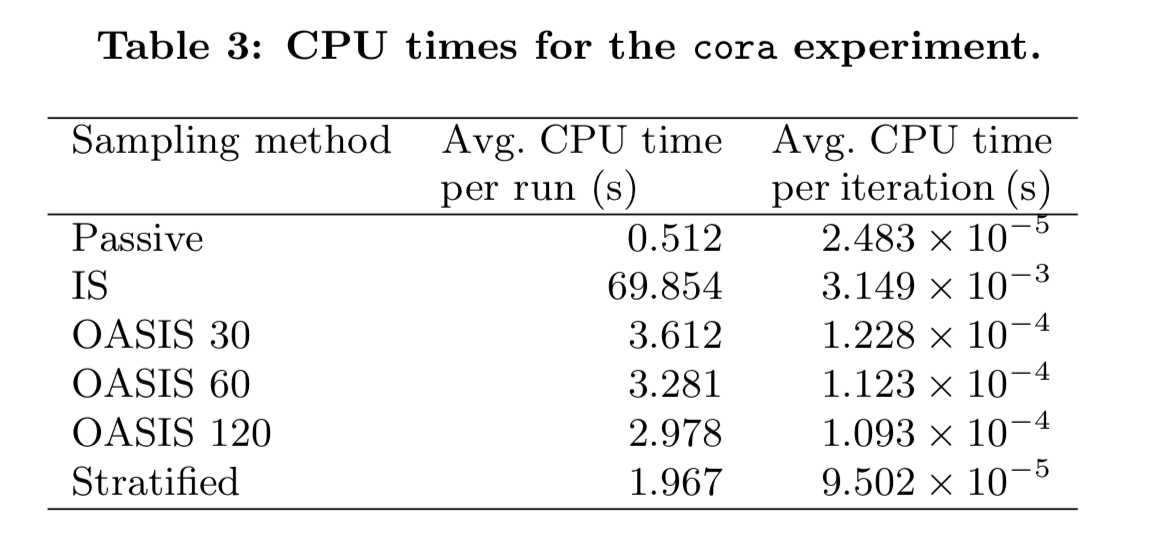
Slightly more time used than passive sampling and stratified sampling
My Point of View
- Solid mathematics
- Very good performance
- Comprehensive experiment