Interpretable Predictions of Tree-based Ensembles via Actionable Feature Tweaking
Outline
- Background
- Problem Formulation
- The solution
- Case Study at Yahoo
Background

Machine learning is usually considered as a black box




I'd really like to know which treatment my patient should undergo to reduce the threat of a heart attack

According to our records, we expect to lower your risk if you will do more fitness







How do we provide such insights?
How do we provide such insights?
We focus on tree(s) models
- Widely used
- Easy to open the black box
Problem Formulation
- First we let \(\mathcal{X} \subseteq \mathbb{R}^n \) be the n-dimentional feature vector space.
- So feature vector is represented as \(\mathbf{x} = (x_1, x_2, ..., x_n)^T \in \mathcal{X}\).
- WLOG, the problem simplified as a binary classification problem, i.e. \(\mathbf{y} = \{-1,+1\}\).
- Also, there's a function \(f: \mathcal{X} \mapsto \mathbf{y}\), i.e. classifier, and \(\hat{f} \approx f\) as the classifier learned from data.
- Here we assume \(f\) to be an ensemble of K tree-based classifiers, i.e. \(\hat{f} = \phi(\hat{h}_1,...,\hat{h}_k)\).
- WLOG, we assume \(\phi\) to be the majority vote.






Goal
\[x' = \arg \min_{X^*} \{1|\hat{f}(x) = -1 \wedge \hat{f}(x^*) = +1 \}\]






Goal
\[x' = \arg \min_{X^*} \{1|\hat{f}(x) = -1 \wedge \hat{f}(x^*) = +1 \}\]
unbound?
- Given a distance measurement \(\delta: \mathcal{X} \times \mathcal{X} \mapsto \mathbb{R}\)
- We want to find a \(x'\) so that
Goal
\[x' = \arg \min_{X^*} \{\delta(x,x^*)|\hat{f}(x) = -1 \wedge \hat{f}(x^*) = +1 \}\]
Goal
\[x' = \arg \min_{X^*} \{\delta(x,x^*)|\hat{f}(x) = -1 \wedge \hat{f}(x^*) = +1 \}\]
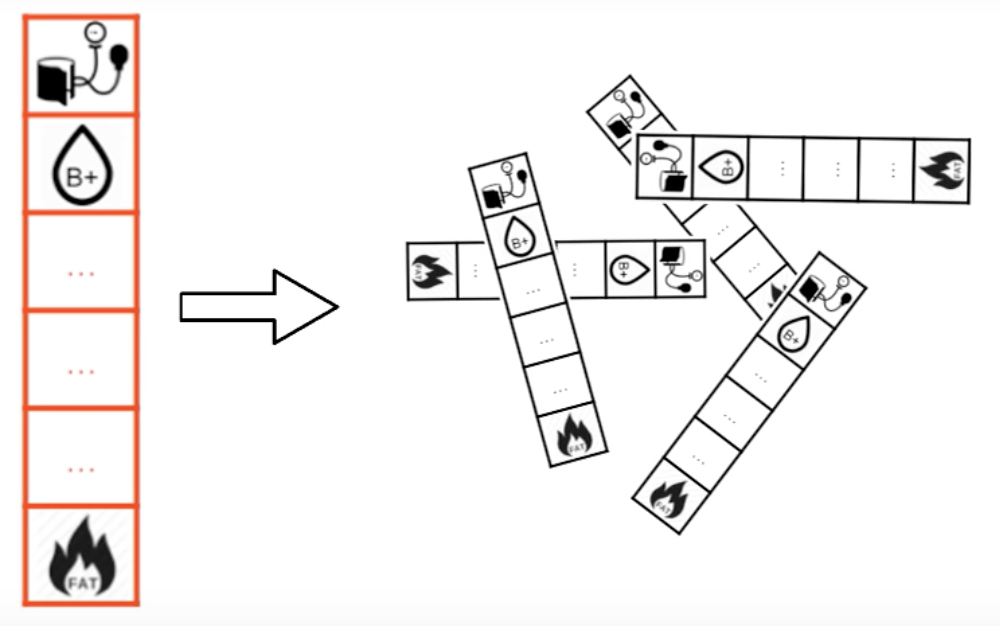
The solution
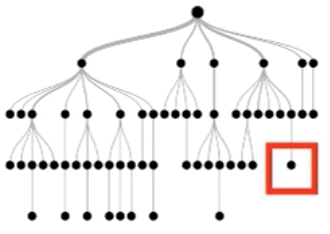
Observation
Each instance follows a root-to-leaf path for each tree

True negative instance
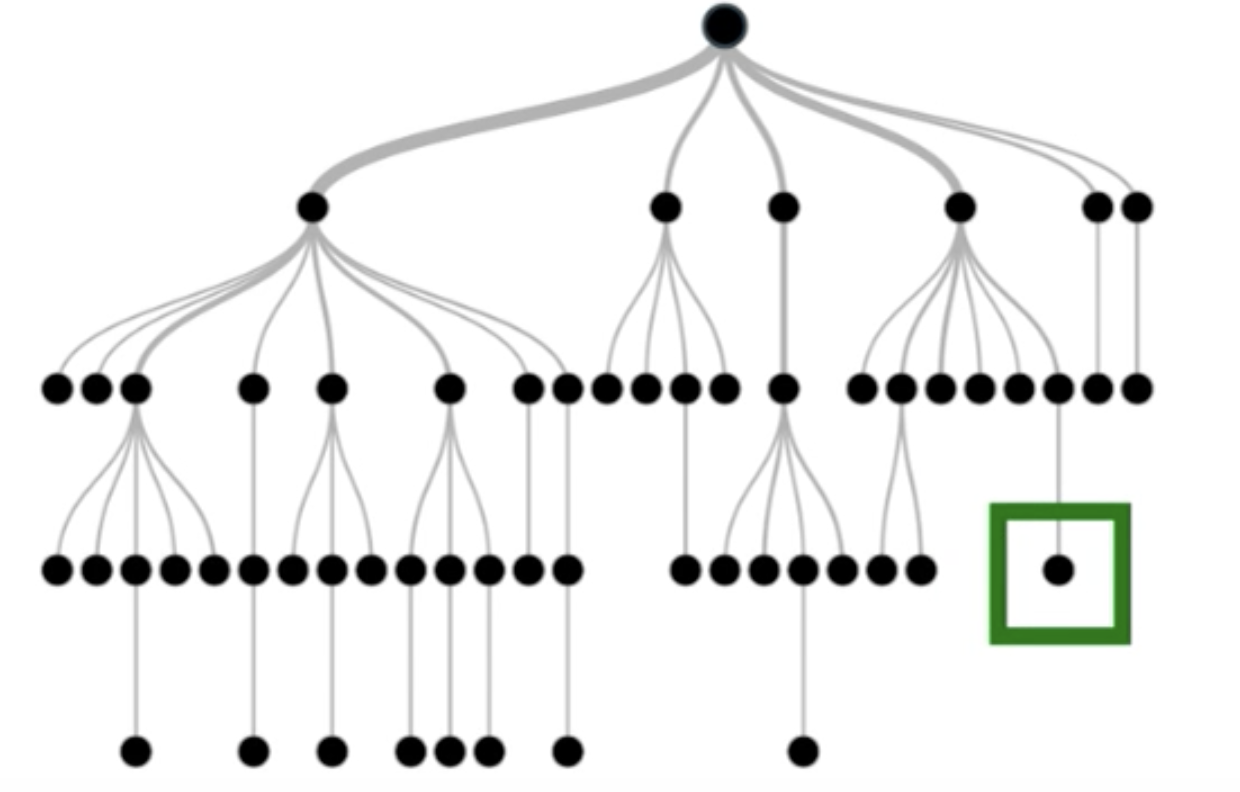
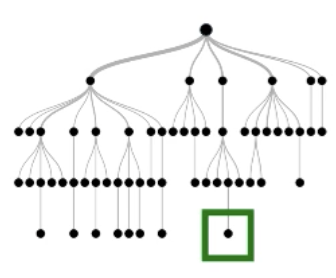
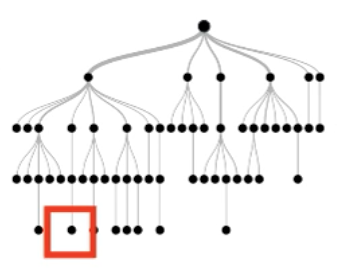
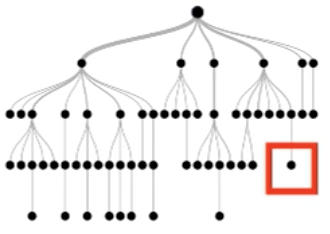
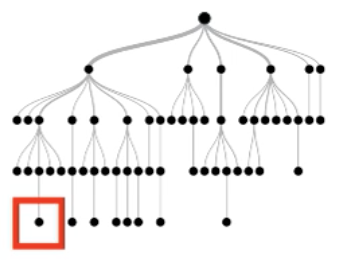
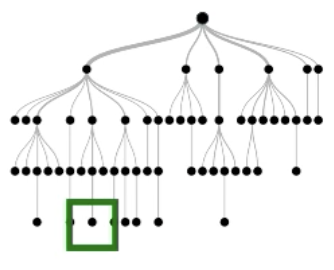
Key Idea
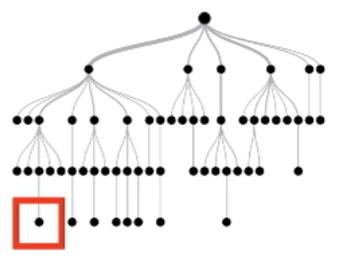
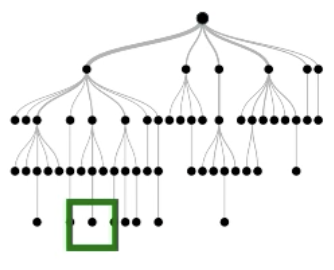
Perturbation
Key Idea


Perturbation
Perturbation: Diff, i.e. a potential suggestion
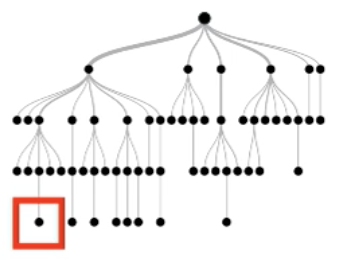
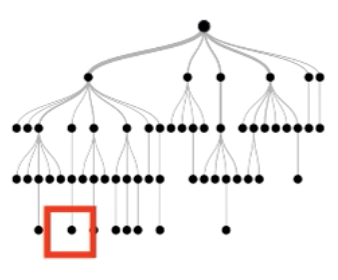
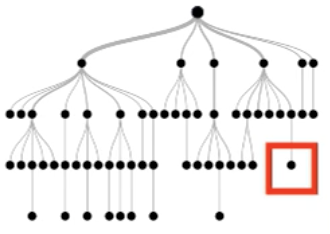
Step 1
Select one tree giving out the negative label
Step 2
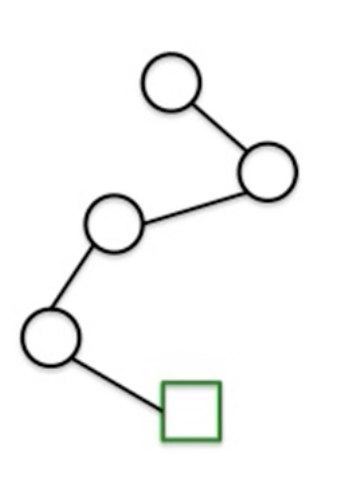
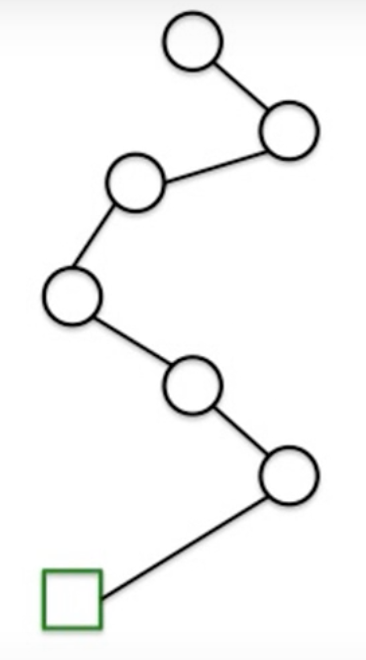
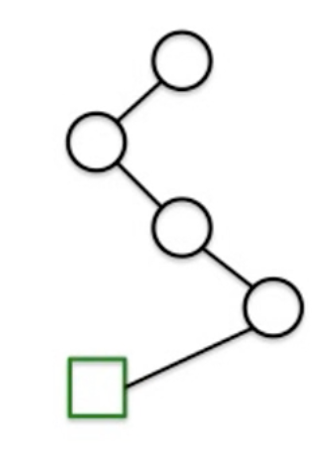
Find all the paths in that tree that outputs positive label
\(\in\)
Step 3
Generate instances satisfying each paths
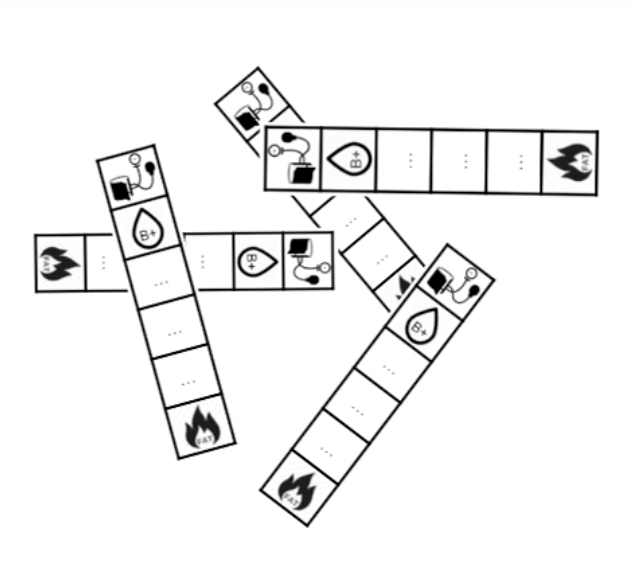

+
=

Formally
- \(p^+_{k,j}\) as the j-th path in tree \(T_k\).
- For all \(T_k \in T^-\), we calculate the perturbed feature vector \(x^+_{j(\epsilon)}\), by
- \(x^+_{j(\epsilon)}[i] = \theta_i - \epsilon \text{ if the i-th condition is } (x_i \leq \theta_i) \) or,
- \(x^+_{j(\epsilon)}[i] = \theta_i + \epsilon \text{ if the i-th condition is } (x_i \gt \theta_i) \)
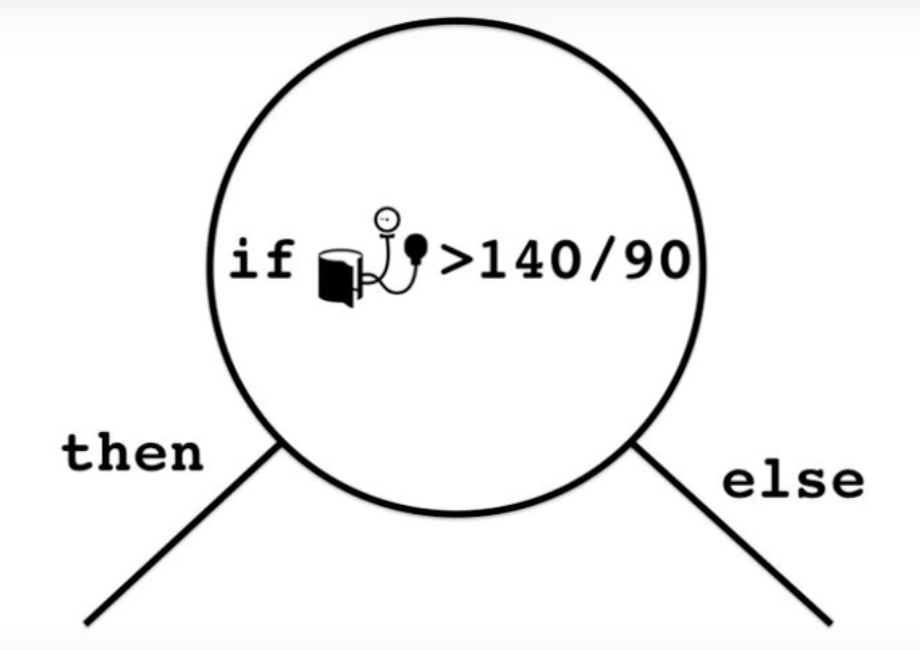

= \(140/90 + \epsilon\)
Problem
Do we need a \(\epsilon\) for every case?
Problem
Do we need a \(\epsilon\) for every case?
Global \(\epsilon\)!
No
Problem
Do we need a \(\epsilon\) for every case?
Global \(\epsilon\)!
No
If all the features is standardized to z-score, then a single \(\epsilon\) is enough.
i.e. \(\theta_i = \frac{t_i - u_i}{\sigma_i}\)
Solution
Problem
Perturb on one tree may invalid other trees
Problem
Perturb on one tree may invalid other trees
Solution
Have a round of check on the whole forest
Recap
- For all trees, get positive paths \(p^+_k\).
- Get perturbed instance \(x^+_{j(\epsilon)}\) by \(buildPositiveInst(x, p^+_{k,j}, \epsilon)\)
- Check if \(\hat{f}(x^+_{j(\epsilon)}) = +1\), and put the instance to a set \(S\)if satisfied.
- For each instances in \(S\), select the one with smallest \(\delta(x, x^+_{j(\epsilon)})\) as \(x'\)
Use case at Yahoo
Ad quality

Ad quality varies, for
Motivation
Ad quality varies, for
Not serving them is not an option
Motivation
Ad quality varies, for
Not serving them is not an option
Serving them hurts the user experience
Motivation
Ad quality varies, for
Not serving them is not an option
Serving them hurts the user experience
As the
Motivation
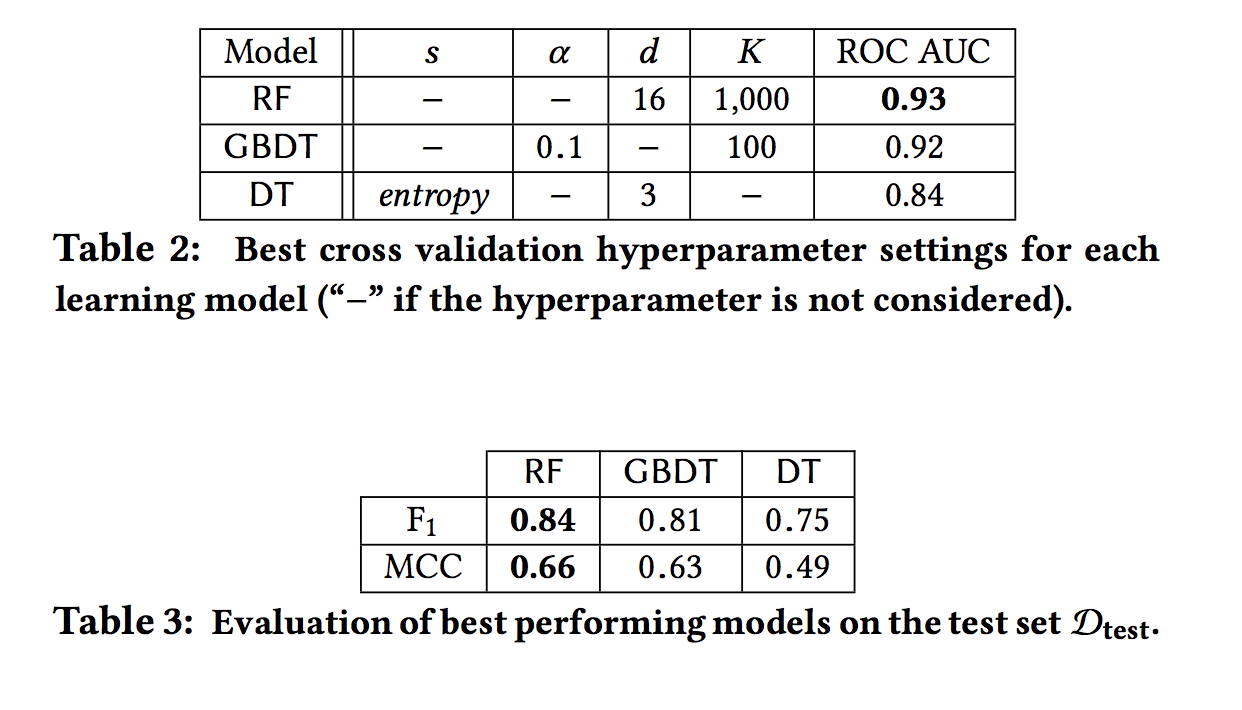
Model settings
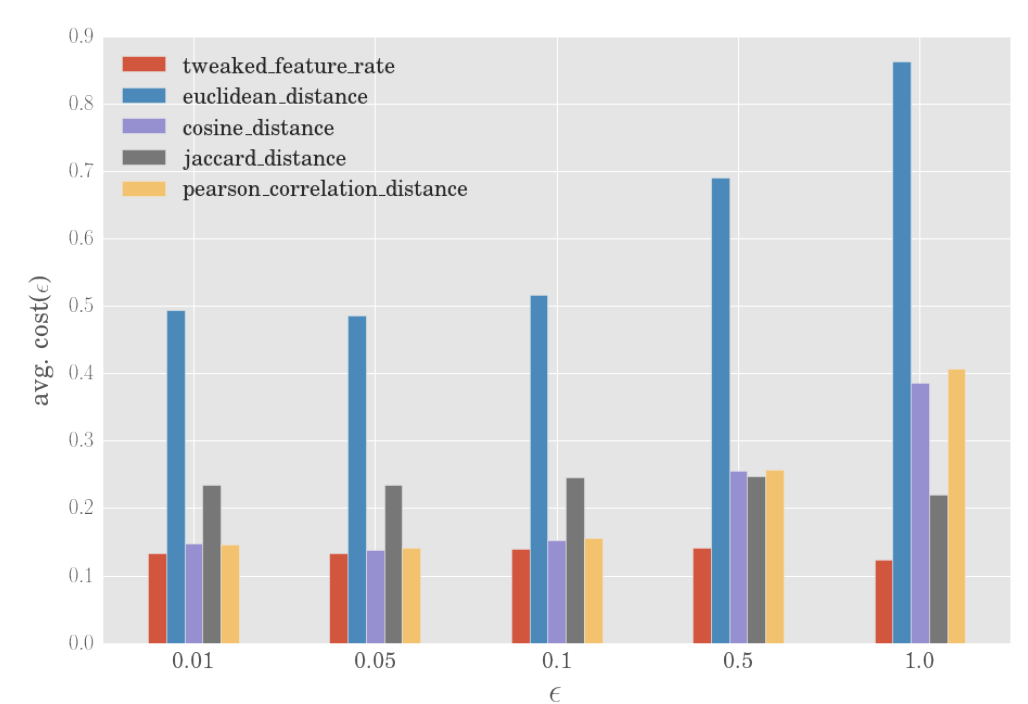
The impact of hyperparameters

Assessing the recommendation quality
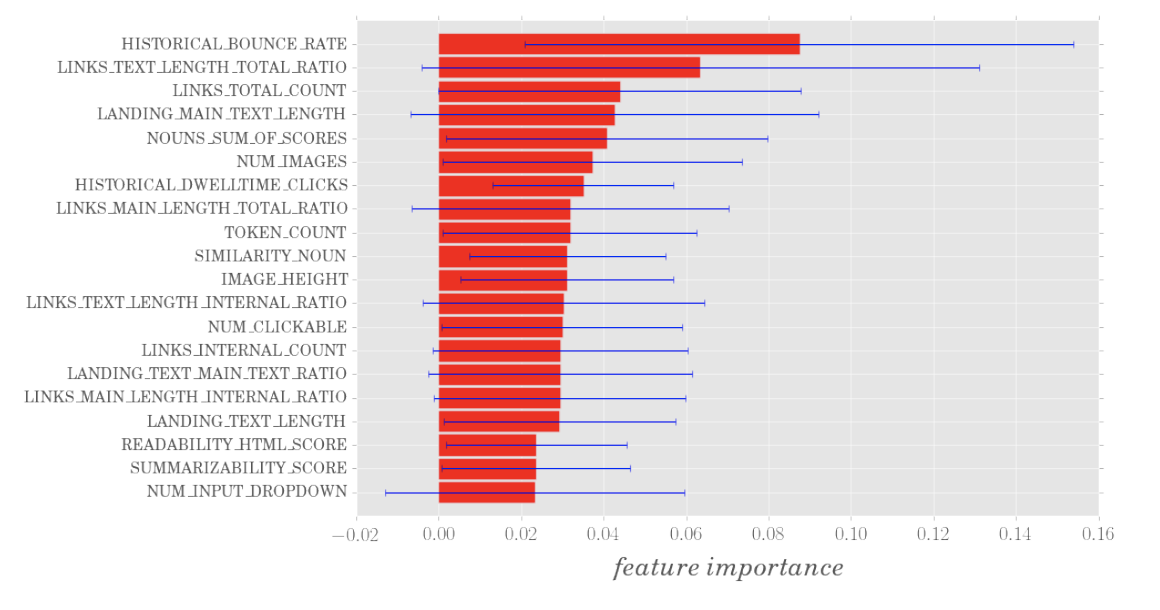
1. Feature ranking
ϵ = 0.05 and δ = cosine distance
Assessing the recommendation quality
2. Top K recommendations based on cost, rank them based on feature importance
ϵ = 0.05 and δ = cosine distance

Assessing the recommendation quality
3. Use user study to test the performance, result shows:
- helpful: 57.3%,
- not helpful: 42.3% (25% neutral)
- not actionable: 0.4%
ϵ = 0.05 and δ = cosine distance
Assessing the recommendation quality
ϵ = 0.05 and δ = cosine distance
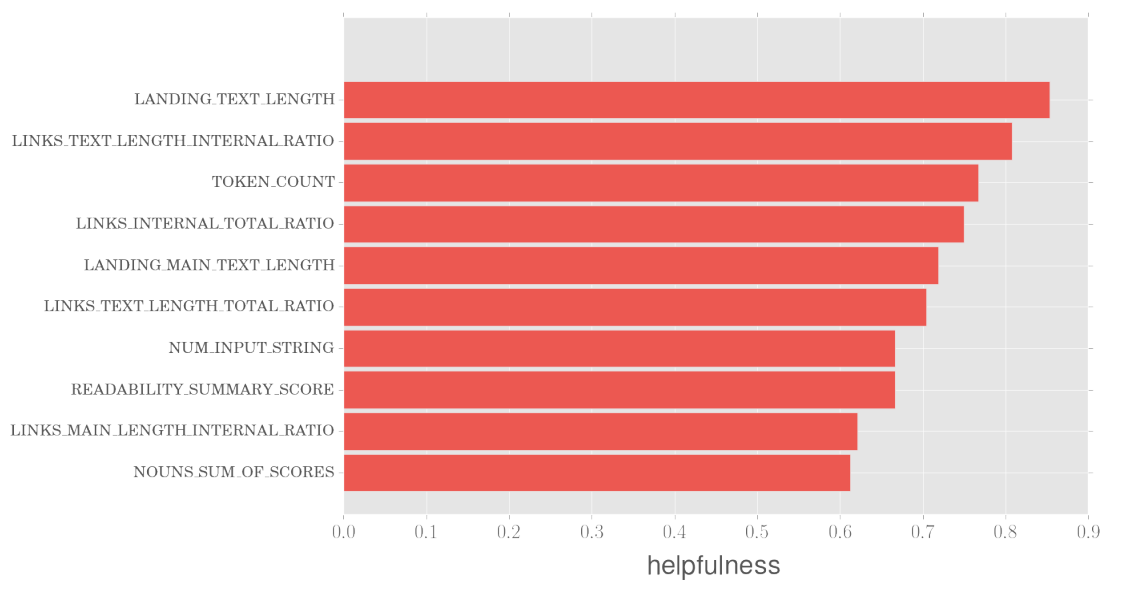
\( helpfulness(i) = \frac{helpful(i)}{helpful(i) + \neg helptul(i)} \)
Showcase of helpfulness for top features
Conclusion
- Not very hard technique
- The real world use case is interesting