Optimization for Active Learning-based Interactive Database Exploration
Data vs Human (Past)

Car for commute, which to choose?

Data vs Human (Now)

Car for commute, which to choose?

Data scale, human don't

Explore-by-Example


Explore-by-Example


Active Learning


Select a point
Interested/Not interested


Select a point
Interested/Not interested
Too much samples required!
Outline
- Problem Setting
- Dual-Space Model (DSM)
- Factorization
- Experiment
Problem Setting
- Table: \(D\), Tuple \(t \in D\)
- Query \(Q^*(t) \in \{true, false\} \) that selects the interested points
Key idea
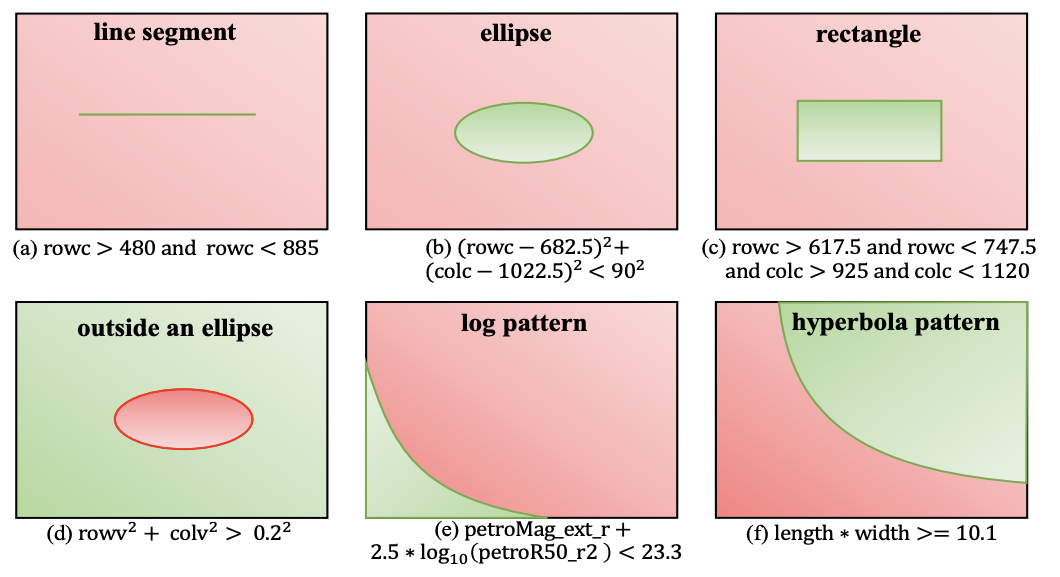
- \(Q^*(t) \in \{true, false\} \) arbitrarily complex? Yes.
- Use active learning blindly, done. Let's call it a day.
- \(Q^*(t) \in \{true, false\} \) arbitrarily complex? No
- Exploit the query selectivity if it is convex, or subspatial convex.
Polytope model
Simple case: convex query.

2D space, 3 positive points.
Green area: all positive!
Polytope model
Simple case: convex query.
2D space, 2 positive points, 1 negative.
Red area: all negative!

Polytope model
Simple case: convex query.

Red: negatives, green: positives, white: uncertain.
Dual-Space Model (DSM)
Simple case: convex query.

Red: negatives, green: positives, white: uncertain.
Obvious
Obvious
Obvious
Obvious
Obvious
Active learning
Active learning
Active learning
1. Uncertain sample a point \(x\)
2. if \(x\) in {red, green}, obvious
3. if \(x\) in white, normal AL
Factorization

What if a query is non-convex?
Factorization

\(rowv^2 + colv^2 > 0.2^2 \text{ AND } 480 < rowc < 885 \)
Observation: Usually conjunctions
Factorization

\(rowv^2 + colv^2 > 0.2^2 \text{ AND } 480 < rowc < 885 \)

Given a conjunction:
factorize
Combine Subspace Result


Given a point \(x\), consider all its subspaces [ , ]:
Case:
Non-convex => output 0,
Positive region => output 1,
Negative region => output -1,
Uncertain region => output 0,
Finally, select the minimal output.
\(+ \wedge ? \Leftrightarrow min(1,0) \Leftrightarrow ?\),
\(+ \wedge - \Leftrightarrow min(1,-1) \Leftrightarrow -\),
Factorization vs Non-factorization

A positive region built from 4 positive points, {A, B, C, and D}
Larger coverage
Training
- Start from 1 positive and 1 negative sample.
- Train machine learning model using current labeled data.
- Derive Polytope from current labeled data (with factorization)
- Uncertainty sample a point based on the ML model.
- Label the data by a human if the polytope cannot decide.
- Go back to 2, or stop if meet the stop criterion.
Stop criterion
- User # interests are small comparing to the table size.
- Active learning: bound for prediction error.
Stop criterion
- User # interests are small comparing to the table size.
Active learning: bound for prediction error.- Unbalanced: we use F1 score.
Stop criterion
- User # interests are small comparing to the table size.
Active learning: bound for prediction error.Unbalanced: we use F1 score.- We don't have a test set, nor affordable to create one.
Stop criterion
- User # interests are small comparing to the table size.
Active learning: bound for prediction error.Unbalanced: we use F1 score.- We don't have a labeled test set, nor affordable to create one.
- \(\frac{|D^+|}{|D^+| + |D^u|}\) is the lower bound of the F1 score.
- Stop if the lower bound reaches some threshold.
\(D^+\): Points in an unlabeled test set is flagged as positive by the polytope
\(D^u\): Points in an unlabeled test set is uncertain to the polytope
Experiments on SDSS

Dataset: 190M tuples, 510 attributes.
Baseline: Active learning (AL), Active Search (AS)
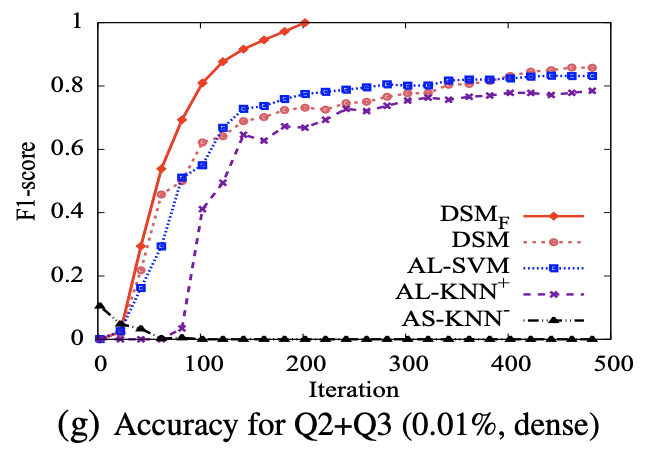
Experiments on SDSS

- DSM = AL-SVM > AL-KNN >> AS-KNN, when sparse
Experiments on SDSS
- DSM > AL-SVM > AL-KNN >> AS-KNN, when dense

Experiments on SDSS

- Lower bound approximation

Experiments on SDSS

\(\gamma\) controls the probability to sample outside the polytope. Small \(\gamma\) suffers from useless samples.
Experiments on SDSS



Experiments on Car Dataset
Dataset: 5622 vehicles with 27 attributes such as the model, year, length, height, engine and retail price.
Users: 11 CS graduates, 7 non-technical persons.
Build \(Q^*\) from Query Trace
1. Given scenario: buying a car for everyday city commute, outdoor sports, an elderly in the family, or a small business.
2. Asked each user to find all the cars that meet the requirements
3. Let the user issue query and check the result then refine the query again until the user is satisfied. -- simulate no explore-by-example system scenario.
Build \(Q^*\) from Query Trace
Generated query has the property:
1. 18 queries are in the range of [0.2%, 0.9%].
2. 117 predicates in total: 70 numerical and convex, 47 categorical and non-convex.
3. All the queries are conjunctive; the only disjunction is applied to the categorical attributes
Experiments on Car Dataset

DSM > AL > Human in user study
Conclusion
- DSM makes uses of the query property to do optimizations which improves the Explore-by-Example performance
- The user study shows that DSM can indeed help analysts save their time.