Optimization of Tree Ensembles
Real World Problem
But also want to know the strategy to make some differences (a.k.a. modify the sample)
When applying a classifier,
sometimes we not only just want to know whether a sample belongs to a class
Examples
- Medical attention
- Company decision
First step
Problem Definition
Given us a classifier $$C(\cdot)$$, and an n-features vector $$X = \{x_1, x_2, ..., x_n\}$$
The object is to find another $$X'$$ so that $$ X' = \arg \max_{X'} C(X') $$
How?
Focus on single model
Random Forest
Random Forest
RF is $$ C(X) = \sum_{t=1}^{T} \lambda_t f_t (\textbf{X})$$ here $$ f_i(\cdot) $$ is a tree in the forest.

Example from Iris dataset
How to formulate the problem?
idea: consider it to be a MIP problem
Terminology
Let $$leaves(t)$$ be the set of leaves or terminal nodes of tree t.
Let $$ splits(t) $$ denote the set of splits of tree t (non-terminal nodes).
Let $$ left(s) $$ be the set of leaves that are accessible from the left branch, and same as the $$ right(s) $$
let $$ V(s) \in \{1, . . . , n\}$$ denote the variable that participates in split s,
and let $$ C(s) $$ denote the set of values of variable i that participate in the split query of s.
Object function
$$ \max_{\textbf{x},\textbf{y}} \sum_{t=1}^{T}\sum_{\ell \in \textbf{leaves}(t)} \lambda_t \cdot p_{t,\ell} \cdot y_{t, \ell} $$
Constraints
- the observation falls in exactly one of the leaves of each tree t
- if 1 observation falls into the a sub-tree, then no observation could fall into the other part of sub-tree
- the indicator y must be in {0, 1}
Intermediate variable
$$ x_{i,j} $$ indicates that if a feature $$X_i$$ fulfills the predicate of that node, i.e. $$X_i$$ falls into left branch of the tree
the observation falls in exactly one of the leaves of each tree t
if 1 observation falls into the a sub-tree, then no observation could fall into the other part of sub-tree
Some additional constraints on x
the indicator y must be in {0, 1}
Trick kicks in!
All in one
Approximation
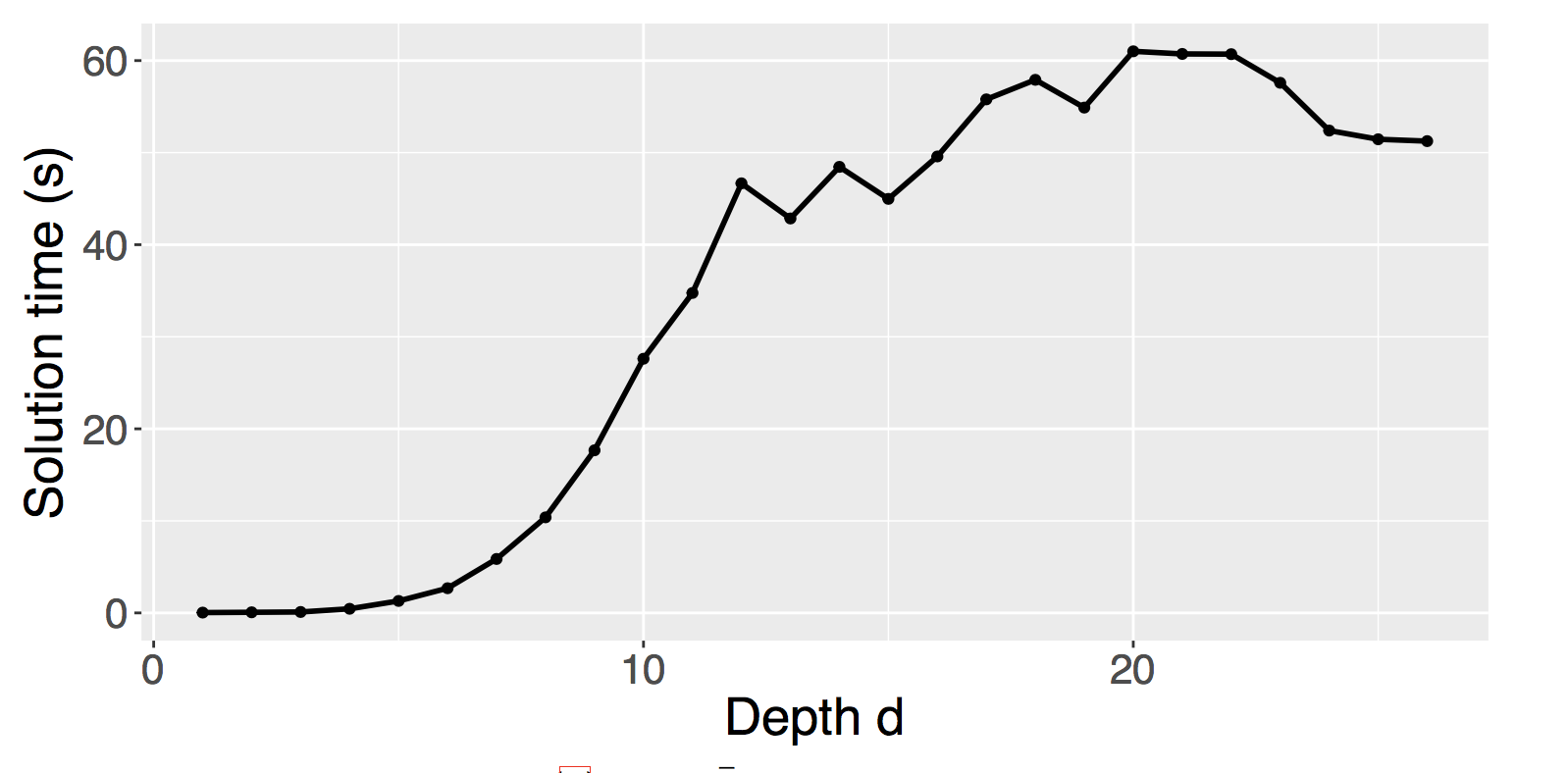
It's quite time-consuming to solve the original problem
Traverse the whole forest, O(k*2^n)!
Idea: what if we do not search to the deepest of the tree?
$$ \Omega = \{(t,s)|t \in \{1,...,T\}, s \in splits(t) \} $$
First define
Proposion
Where Z is the objective value
Theorem

Experiments
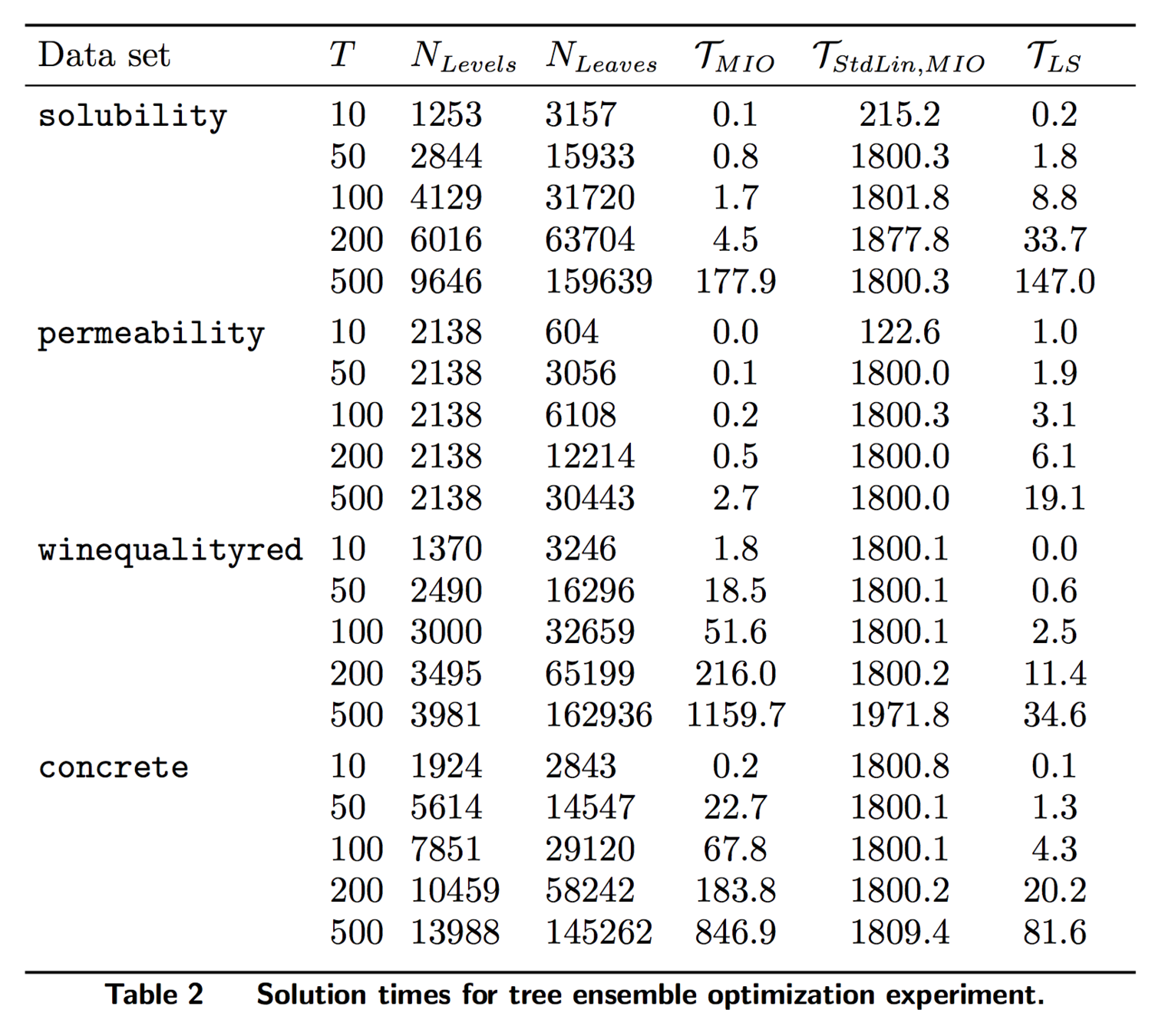
Experiments
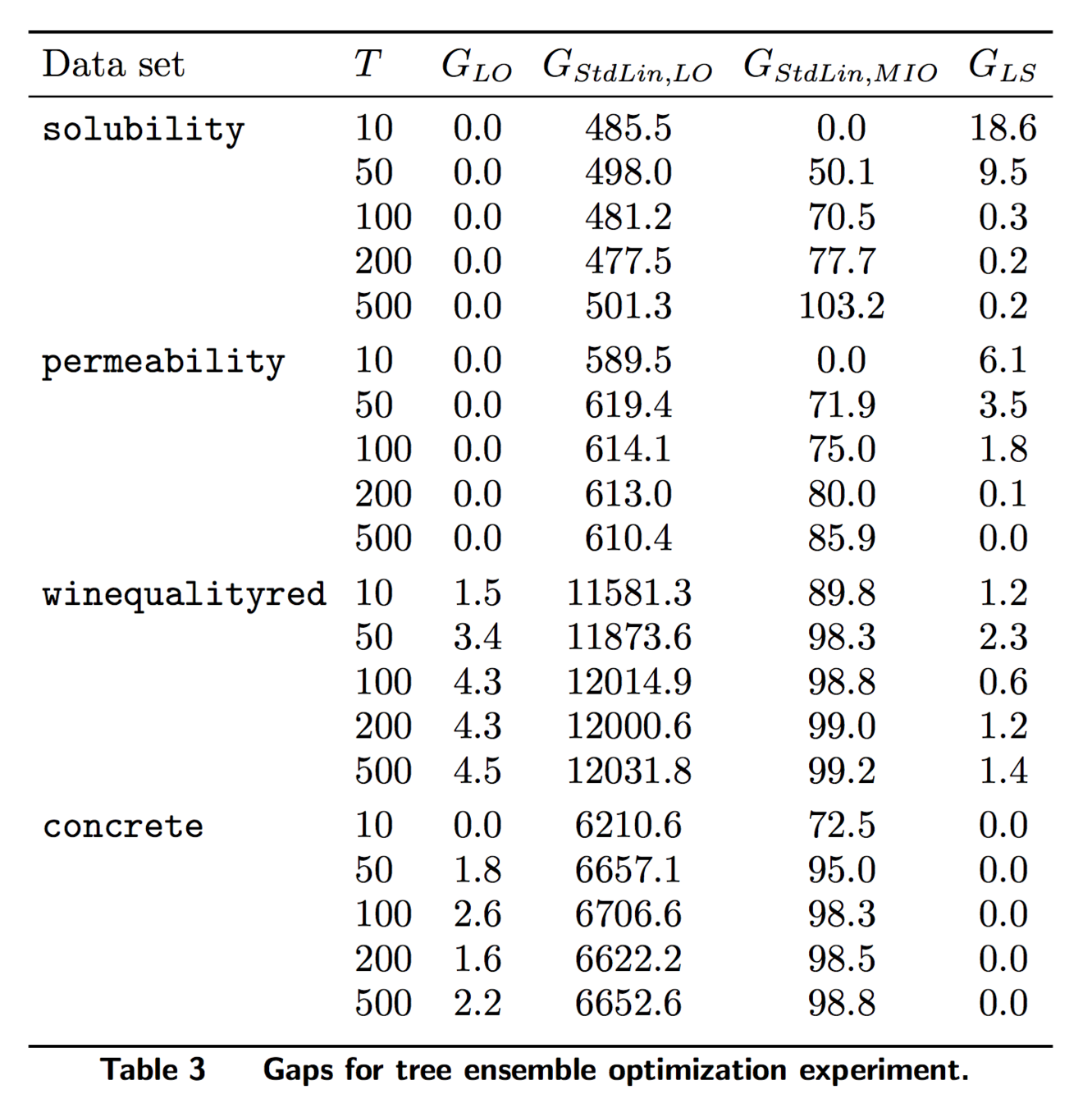
Experiments