Improving Latent Factor Models via Personalized Feature Projection for One Class Recommendation

Tong Zhao, Julian McAuley, Irwin King

CIKM'15

Motivation (1/2)

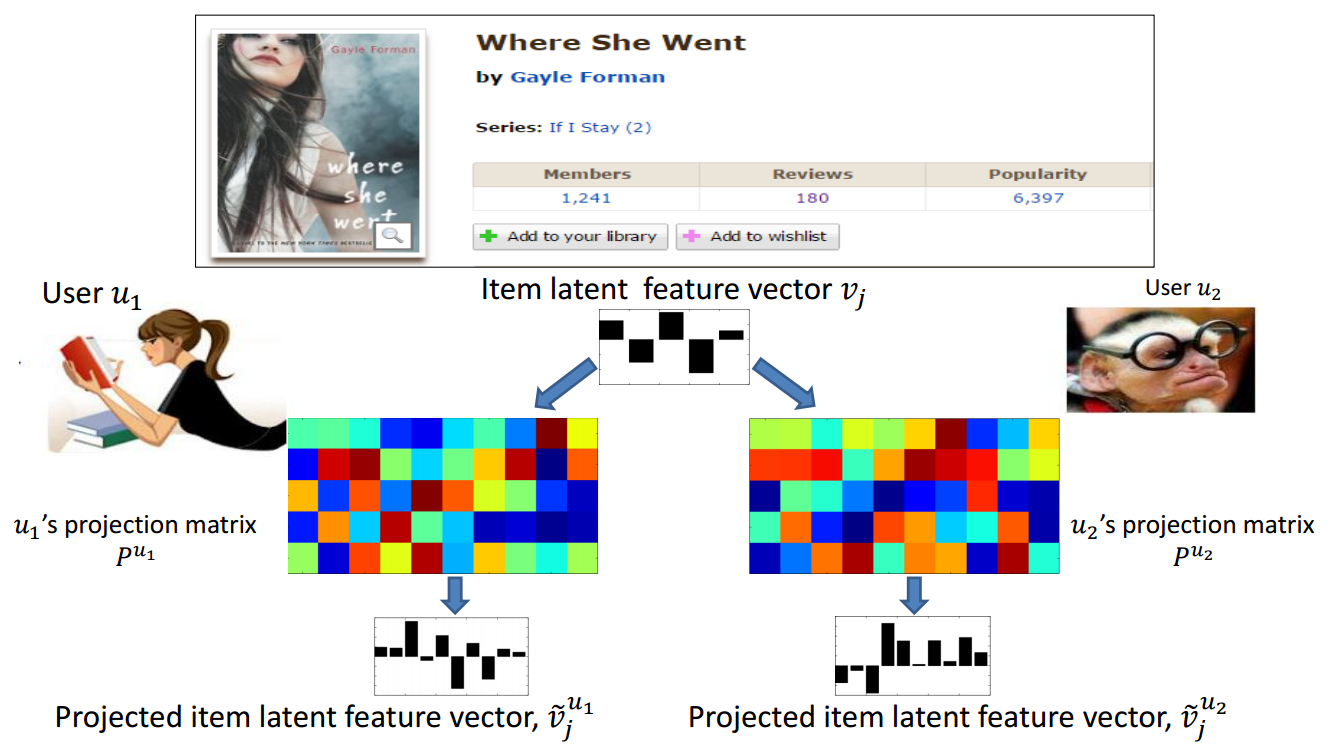
  • Latent factor models use inner product to represent a user's compatibility with an item.
  • However, a user’s opinion of an item may be more complex.
    • Each dimension of each user’s opinion may depend on a combination of multiple item factors simultaneously.
    • It may be better to view each dimension of a user’s preference as a personalized projection of an item’s properties.

Motivation (2/2)

  • A personalized feature projection (PFP) method is proposed to learn users’ latent features as a personalized projection matrix instead of a vector.
  • A user's opinion of an item is no longer modeled by a real number but a vector.
  • Vector-based objectives can be formulated, which provides more flexible structures to describe users’ preferences.

5

5

10

10

Methodology (1/10)

  • Each user is modeled as a personalized projection matrix.

     
  • For a specific user u, each item vector is projected by multiplying u’s personalized projection matrix.

     
  • When K*=1, PFP reduces to the original latent factor model.
P^u=R^{K \times K^*}, P^u_f=R^K
Pu=RK×K∗,Pfu=RKP^u=R^{K \times K^*}, P^u_f=R^K
\tilde{v_j}=v_jP^u
vj~=vjPu\tilde{v_j}=v_jP^u

Methodology (2/10)

  • Then u's preference toward item j is modeled by summarizing all the projected feature vectors from his / her positive feedback.


     
  • Assumption: The projected feature vectors of users’ positive feedback items should be closer to users’ average taste than are the negative feedback items.

     
  • The average similarity makes the approach insensitive to the choice of which positive feedback items should be selected.
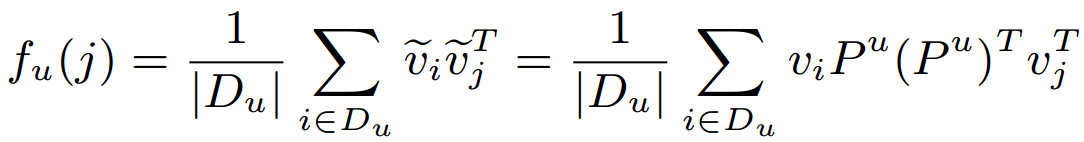
f_u(i) \succ f_u(j)
fu(i)≻fu(j)f_u(i) \succ f_u(j)

Methodology (3/10)

  • Personalized Feature Projection (PFP) for one class recommendation.
  • Three objective functions for optimizing ranking:
    • Area under the ROC curve (AUC) Loss
    • Weighted Approximated Ranking Pairwise (WARP) Loss
    • Kullback–Leibler divergence (KL-divergence)

Methodology (4/10)

  • Area under the ROC curve (AUC) Loss
    • Apply Bayesian Personalized Ranking (BPR) framework.

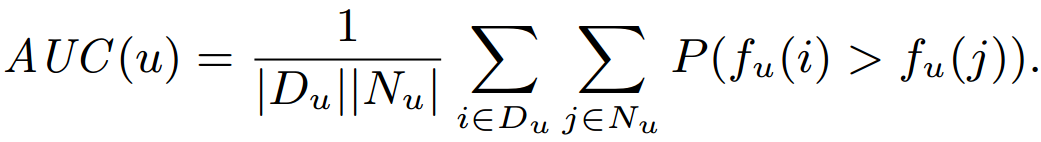
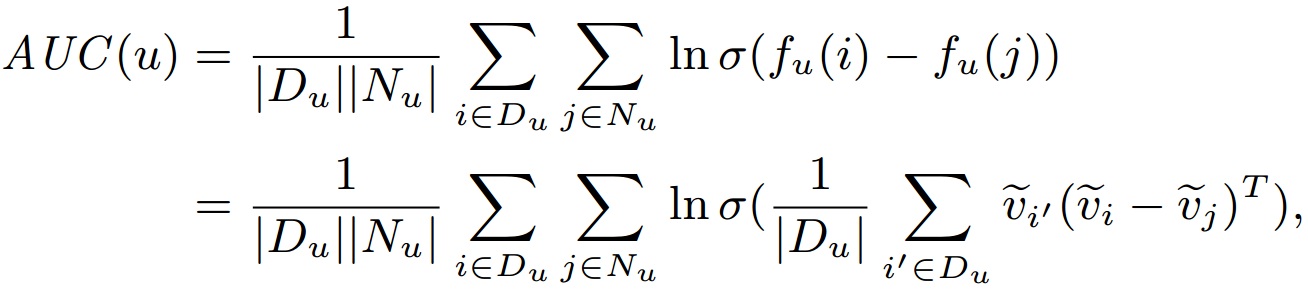
Methodology (5/10)

  • Weighted Approximated Ranking Pairwise (WARP) Loss



     
    • Θ is a function which transforms the predicted rank of item i into a loss value.

       
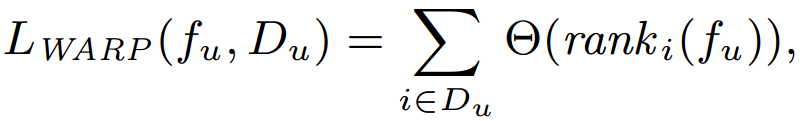
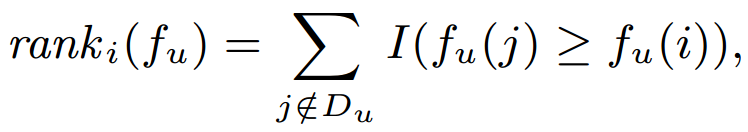
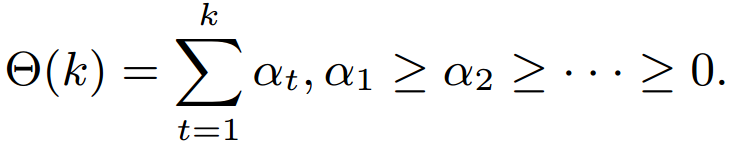
\alpha_t=\frac{1}{N}
αt=1N\alpha_t=\frac{1}{N}
\alpha_t>\alpha_{t+1}\ \ e.g.\ \frac{1}{t}
αt>αt+1  e.g. 1t\alpha_t>\alpha_{t+1}\ \ e.g.\ \frac{1}{t}
Optimize mean rank
Assign higher importance to the top-ranked item

Methodology (6/10)

  • Weighted Approximated Ranking Pairwise (WARP) Loss




     
    • Since computing                  costs too much, we uniformly sample a negative feedback instance until a pairwise violation is found.

      where Q is the steps required to find a pairwise violation
'
′'
'
′'
'
′'
rank^{'}_i(f_u)
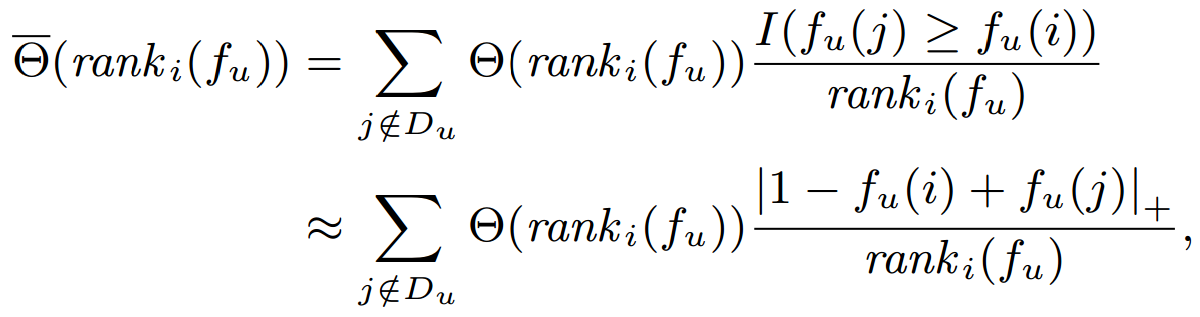
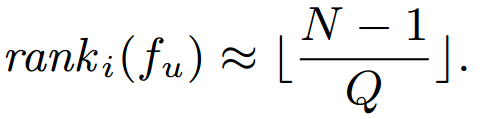
ranki′(fu)rank^{'}_i(f_u)

Methodology (7/10)

  • Weighted Approximated Ranking Pairwise (WARP) Loss
    • ​The loss of a chosen (u, i, j) triple becomes

       
    • Apply gradient descent to perform updates.

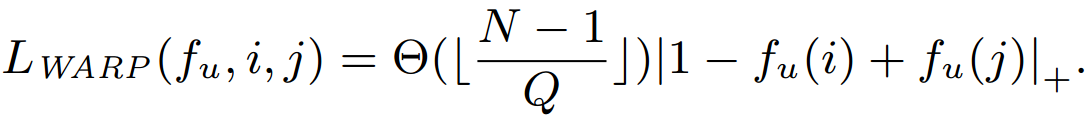
Methodology (8/10)

  • Kullback–Leibler divergence (KL-divergence)
    • PFP models a user's preference on an item via a projected vector.
    • Thus users’ preference differences on items can be modeled in vector space.
    • Maximize the KL-divergence between the projected vectors from users’ positive and negative instances.
    • KL-divergence

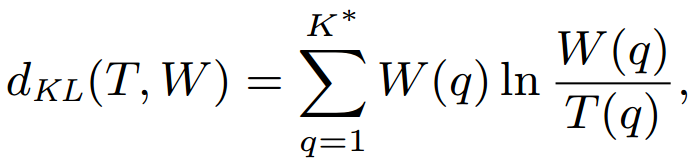
Methodology (9/10)

  • Kullback–Leibler divergence (KL-divergence)
    • Objective function for a pair of positive and negative item (i, j)

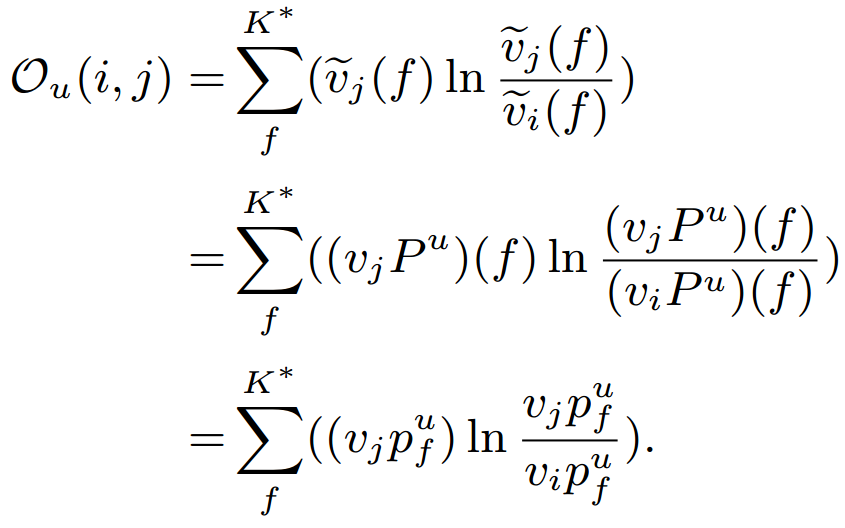
Methodology (10/10)

  • Kullback–Leibler divergence (KL-divergence)
    • Apply gradient ascent to perform updates.






       
    • Some constraints to avoid overfitting.

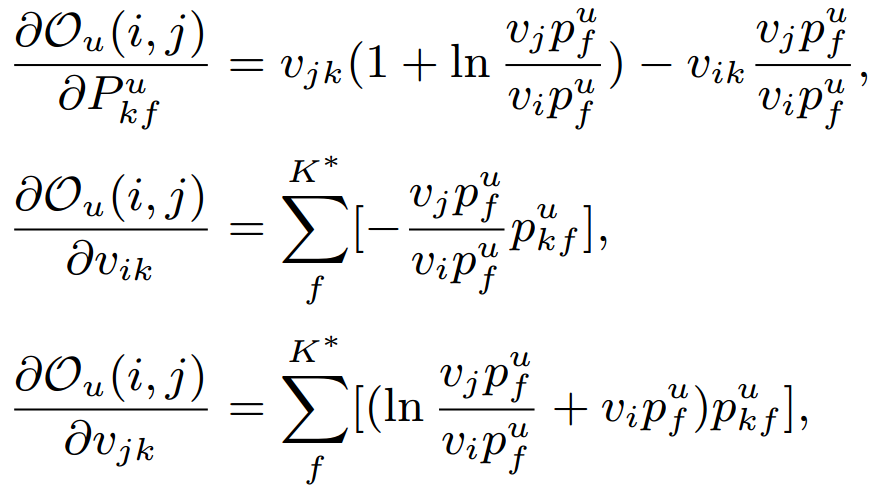
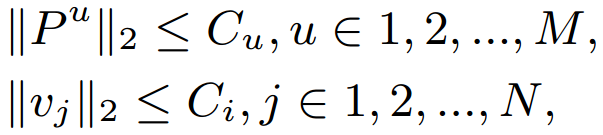
Experiments (1/5)

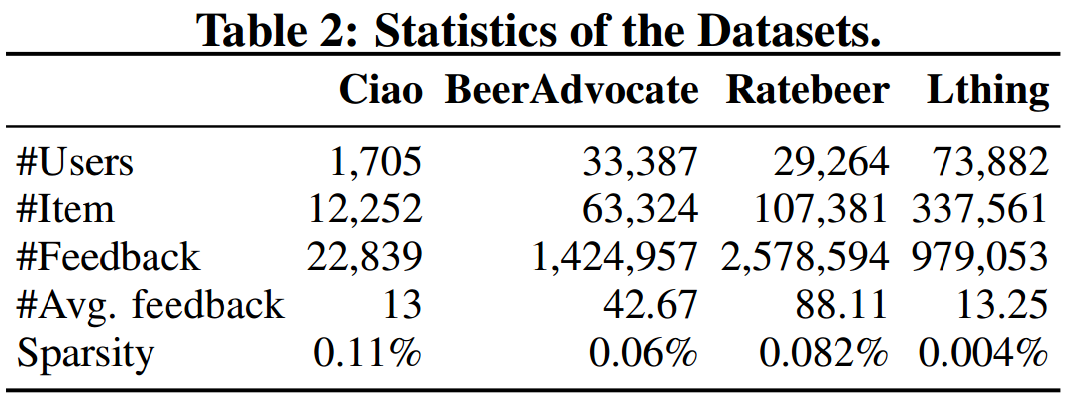
  • Datasets





     
    • Keep ratings >= 4 to make positive feedbacks.
    • Randomly split 10% ratings to be testing.
  • Evaluation metrics
    • AUC
    • NDCG

Experiments (2/5)

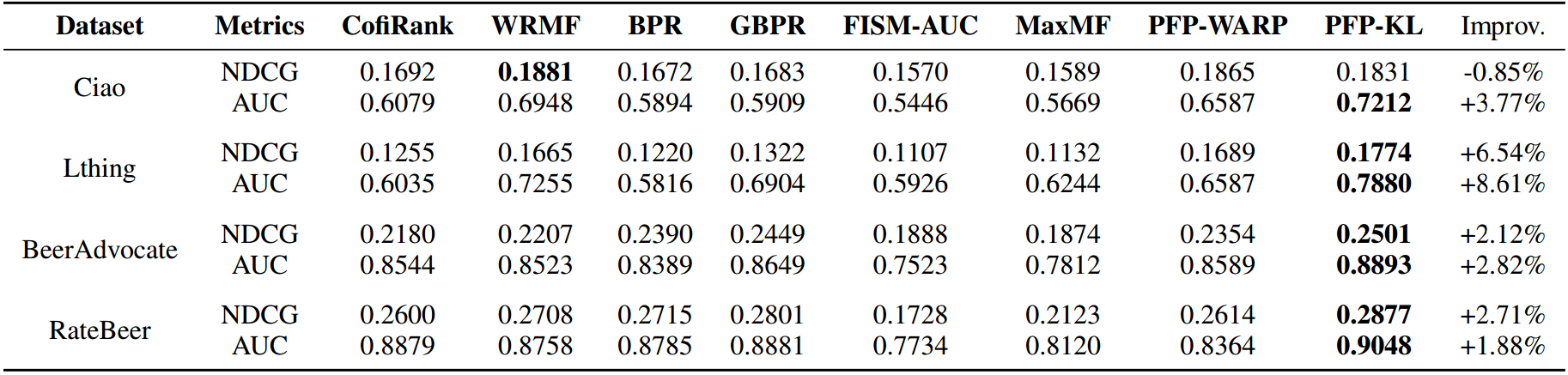
PFP-KL generally outperforms PFP-WARP

Experiments (3/5)

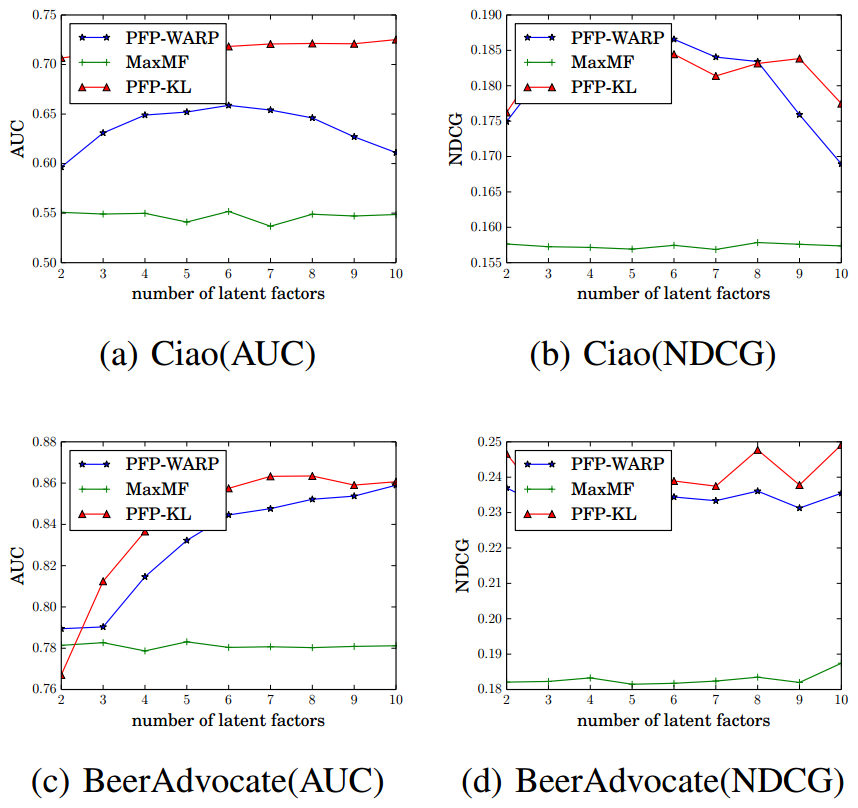
Embedding size is too small...

  • Impact of #latent factors

Experiments (4/5)

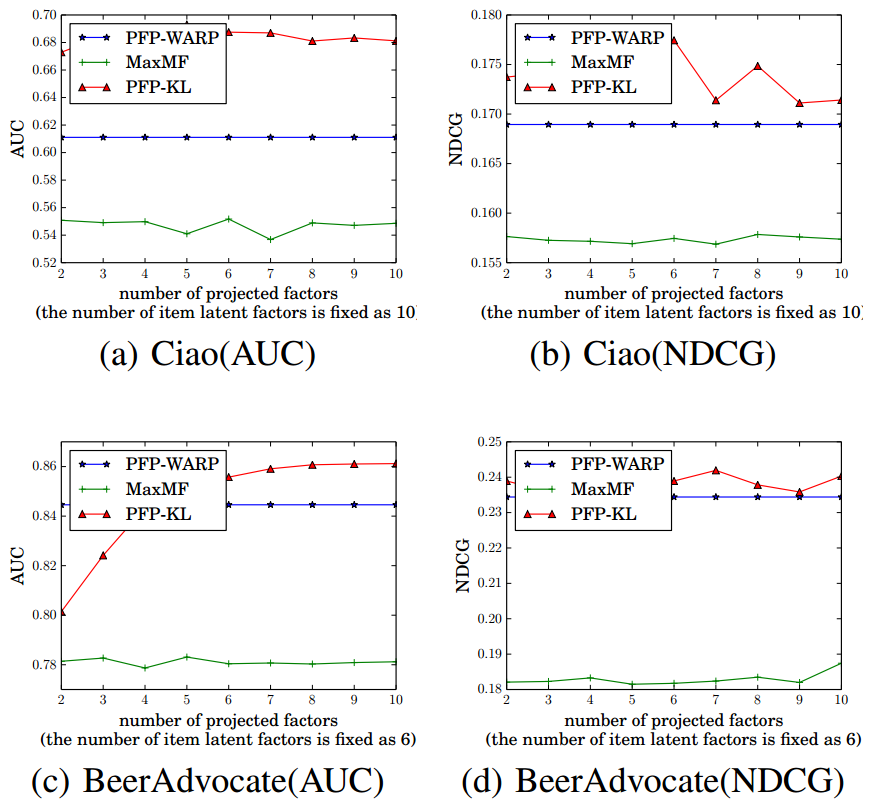
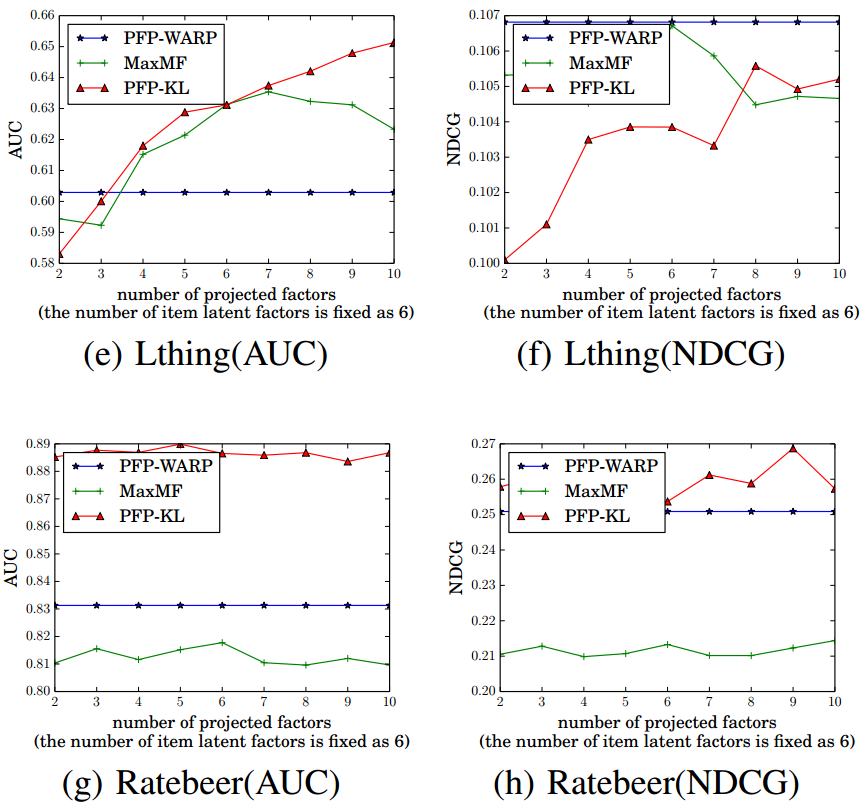
  • Impact of #projected factors

Q: Why does PFP-WARP's performance is independent of #projected factors ?

Experiments (5/5)

  • Observations
    • When K* is small, PFP-KL cannot make use of such a low-dimensional projection space to describe users’ preferences.
    • When observed feedback is sufficient for training, a large projection number can be applied to better model user tastes.
    • When limited observed feedback is provided, the projection number should be decreased to avoid overfitting.

Conclusion

  • The authors proposed Personalized Feature Projection (PFP) method to capture the complexities of users' preferences towards certain items over others.
  • PFP assumes each dimension of a user’s preference is related to a combination of item factors simultaneously.
  • It is unclear of the meaning behind each projected latent factor.
Made with Slides.com