InvFBA (and more)
From re-implementing an existing method to developping a "new" one
Combi meeting, 29/11/2017
Key Idea


Gain insight into the metabolic goals of the organism
Gene expression
Metabolic network
Can we compare the landscape of metabolic goals... :
- ... of individuals grown on different conditions ?
- ... across time ?
- etc...
Some questions of interest
Recap on metabolic network

- Set of all chemical reactions of metabolism
- Metabolic pathways : glycolysis, ...

Recap on metabolic network
| 1 | 2 | |
|---|---|---|
| A | -2 | 0 |
| B | -1 | 0 |
| C | 1 | -1 |
| D | 0 | 1 |
Stoichiometric matrix
Bipartite weighted directed graph
R1 : 2A + B -> C
R2 : C <-> D

Recap on metabolic network

Gene expression
Enzyme
Reaction catalysis
Gene Protein Reaction (GPR) association :
rxn_1984 : (gene_b OR gene_c) AND gene_d
rxn_1983 : gene_a

FBA
Flux Balance Analysis
Calculates the flow of metabolites through the metabolic network, given :
- stoichiometric constraints
- bounds on fluxes
- an a priori defined objective (often biomass maximization)
- the steady state hypothesis
$$max \ cv$$
s.t.$$ Sv = 0 $$
$$L \leq v \leq U$$
Mathematical description
Simulation purpose
- gene deletion
- growth media optimization
- ...
steady state constraint
Biomass maximization
$$max \ v_{biomass}$$
s.t.$$ Sv = 0 $$
$$L \leq v \leq U$$
$$v=(v_1,...,v_n)$$$$c = (c_1,...,c_n)$$
$$L = (L_1,...,L_n)$$
$$U=(U_1,...,U_n)$$
$$S=(s_{j,i})_{1 \leq j \leq m, 1 \leq i \leq n} $$
m : number of metabolites
n : number of reactions
inv-FBA
FBA drawbacks :
- Inadequacy of the biomass function
- Organism goal may not be the biomass maximization


Motivation
Zhao Q. et al., Gen. Bio., 2016
inv-FBA
Plus of Lee et al. method:
- no a priori objective function
- no need for multiple transcriptomics dataset
- no need to define a threshold for genes high/low expression state
is not enough
inv-FBA limits :
- MATLAB implementation
- Works with fluxes as input
Find a way to go from gene expression to fluxes

Lee et al., BMC Systems Biology, 2012
No gold standard
Workflow



| GENE EXPRESSION TO "REACTION EXPRESSION" (GPR association) |
|---|
Gene expression
Metabolic network
External database
| Mean | SD | |
|---|---|---|
| reaction 1 | 8 | 2 |
| reaction 2 | 4 | 1 |
| REACTION EXPRESSION TO FLUX (Lee et al.) |
|---|
| Flux | |
|---|---|
| reaction 1 | 0,0017 |
| reaction 2 | 0,02 |
| InvFBA |
|---|


METABOLIC GOALS
"Reaction expression"
Flux
RNA-Seq data :
- SAMOSA
- Normalized with Deseq2
- Conditions : Light, temperature, time
- Triplicates
Metabolic network built with

Focus on two conditions
- WH7803_LLCtT0
- WH7803_LLUVT6
Demonstration with synechococcus
Workflow



| GENE EXPRESSION TO "REACTION EXPRESSION" (GPR association) |
|---|
Gene expression
Metabolic network
External database
| Mean | SD | |
|---|---|---|
| reaction 1 | 8 | 2 |
| reaction 2 | 4 | 1 |
"Reaction expression"
Compute mean and standard deviation across samples for each gene
SD will be used as a confidence parameter when building fluxes
From gene expression to reaction expression
| Sample 1 | Sample 2 | Sample 3 | |
|---|---|---|---|
| gene_1 | 8 | 7 | 9 |
| gene_ 2 | 4 | 2 | 10 |
| ... |
| Mean | SD | |
|---|---|---|
| gene_1 | 8 | 1 |
| gene_ 2 | 5.3 | 4.16 |
| ... |
Evaluate reaction expression

reaction_1 : (B and C) or A
Abstract Syntax Tree (AST)
gene-protein-reaction (GPR) association
| Gene name | Gene expression |
|---|---|
| A | 12 |
| B | 3 |
| C | 7 |
B and C : min(3,7) = 3
(B and C) or A : 3 + 12 = 15
reaction_1 : 15
Metabolic network :
- 1095 reactions (656 reversibles)
- 1221 metabolites
- 540 "known" genes
209/1095 reactions for which we can't compute an expression
RNA-Seq data :
- 3 replicates per condition
- 2544 genes (including the 540)
209 Gene-Protein-Reaction rules (GPR) untractable :
- 111 containing only "Unknown"
- 65 empty
- 33 mixing known and unknown genes
Demonstration with synechococcus
Workflow



| GENE EXPRESSION TO "REACTION EXPRESSION" (GPR association) |
|---|
Gene expression
Metabolic network
External database
| Sample 1 | Sample 2 | |
|---|---|---|
| reaction 1 | 8 | 2 |
| reaction 2 | 4 | 1 |
| REACTION EXPRESSION TO FLUX (Lee et al.) |
|---|
| Flux | |
|---|---|
| reaction 1 | 0,0017 |
| reaction 2 | 0,02 |

"Reaction expression"
Flux
Lee
$$Z = min\sum_i \frac 1 {\sigma_i} | v_i - d_i |$$
s.t.$$ Sv = 0 $$
$$L_i <= v_i <= U_i$$
$$d_i :$$
$$v_i :$$
reaction flux
reaction expression
$$\sigma_i :$$
reaction expression standard deviation
Problem with reversible reactions : flux can be positive or negative when expression is always positive
Maximize the correlation between the predicted fluxes and the corresponding gene expression data

$$V_{Irr} = \{r_1,r_2,r_3\}$$
$$V_{Rev} = \{r_4,r_5\}$$
$$Z_{Irr} = 2.5$$
$$1 \leq v_4 \leq 7$$
$$-2 \leq v_5 \leq 8$$
$$V_{Irr} = \{r_1,r_2,r_3,r_4\}$$
$$Z_{Irr} = 2.8$$
$$-2 \leq v_5 \leq 5$$
$$V_{Irr} = \{r_1,r_2,r_3,r_4\}$$
Demonstration with synechococcus
Only 61 reversible reactions remaining
Synechococcus
1095 reactions
656 reversible
439 irreversible
Before Lee
After Lee
Run a FBA without any objective to assign a flux to those reactions
Workflow



| GENE EXPRESSION TO "REACTION EXPRESSION" (GPR association) |
|---|
Gene expression
Metabolic network
External database
| Sample 1 | Sample 2 | |
|---|---|---|
| reaction 1 | 8 | 2 |
| reaction 2 | 4 | 1 |
| REACTION EXPRESSION TO FLUX (Lee et al.) |
|---|
| Flux | |
|---|---|
| reaction 1 | 0,0017 |
| reaction 2 | 0,02 |
| InvFBA |
|---|


METABOLIC GOALS
"Reaction expression"
Flux
InvFBA
Step 1

optimal solution of FBA
Seek a vector c that makes all measurements flux vectors as close as possible to optimal flux distributions in the FBA problem
$$x_i$$
Duality theory
$$q^i_2x_{ub} - q^i_1x_{lb} = cx^*$$

$$c^{step_1}=(0.23,0,0.52,0.25,0)$$
InvFBA
Step 2

Find a sparser vector c to help the biological interpretation of the solution
$$c^{step_1}=(0.23,0,0.52,0.25,0)$$
$$c^{step_2}=(0,0,1,0,0)$$
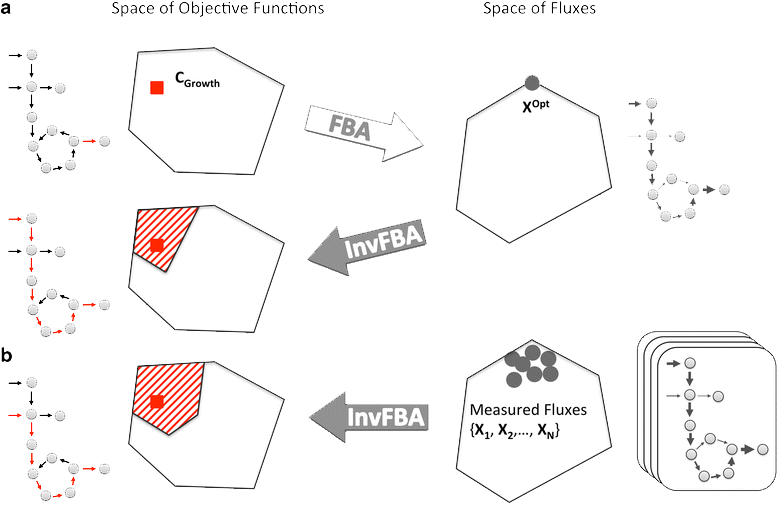
Schematic representation of how FBA and invFBA work
Zhao Q. et al., Gen. Bio., 2016
OVA
Objective Variability Analysis
OVA determines the range each reaction coefficient can take
There exists possibly an infinity of invFBA solutions

$$ 0 \leq c^{min}_i \leq c_i \leq c^{max}_i \leq 1$$
Comparing objective function space

Main modules
- cobrapy : handle metabolic network, FBA analysis
- ast : tree structure to interpret boolean expression
- gurobipy : optimization solver , LP
Python modules
- pandas : data frame handling
- scipy : sparse matrix
Visualization
- plotly
- highcharts
- jinja2 + d3js
Technical
- Some adjustments required on Lee's method
- Return more solutions from Lee's method to give as input to invFBA
- Parallelization
Validation
- Apply the method to all SAMOSA experimental conditions
- Biological interpretation of coefficients values
- Test for statistical significance
Package the program using
Ongoing and future work
