Breaking RSA

Cesena Security Network and Application

hard as solving the factoring problem

Asymmentric Key Cryptography

or Public-Key Cryptography

RSA algorithm was publicated by Rivest, Shamir, Adleman
Diffie and Hellman introduced public-key cryptography in 1976 (using RSA)
The two keys are use to encrypt (public) and decrypt the data (private)
Based on mathematical calculation

Text

Key Generation

Choose two prime number p and q
Compute n = p * q
Compute:
Choose an integer e s.t. 1 < e < λ(n) and gcd(e, λ(n)) = 1
Determine d as d * e ≡ 1 * mod(λ(n)):
d is used as the private key exponent
e is used as the public key exponent

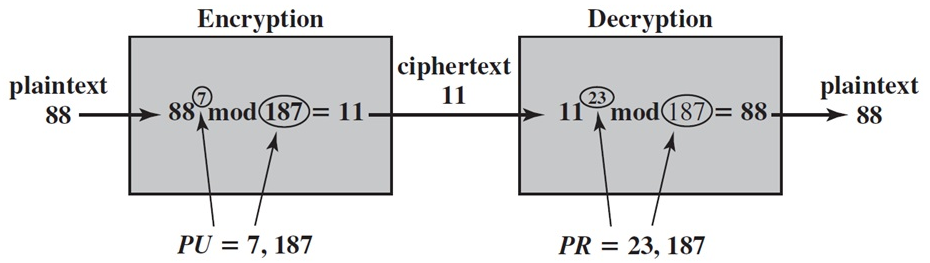
\lambda(n) = lcm( \lambda(p), \lambda(q) ) = lcm( p-1, q-1 )

\lambda(n) = lcm( \lambda(p), \lambda(q) ) = lcm( p-1, q-1 )

How it works?

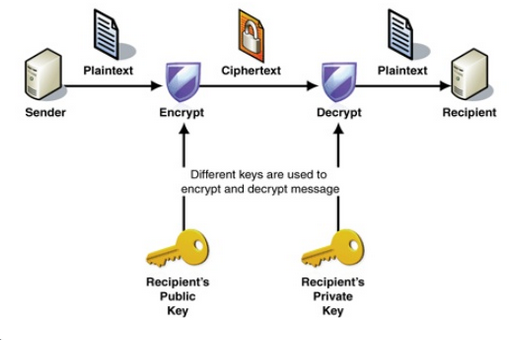
Alice shares securly her public key
Bob can pick up the her public key
Bob (the sender) use the Alice's public key to encrypt the message
Alice and only Alice can decrypt the message with her private key

Encryption

Decryption

n = p * q

c \equiv m^e (mod n)

c \equiv m^e (mod n)

c^d \equiv (m^e)^d \equiv m (mod n)

c^d \equiv (m^e)^d \equiv m (mod n)

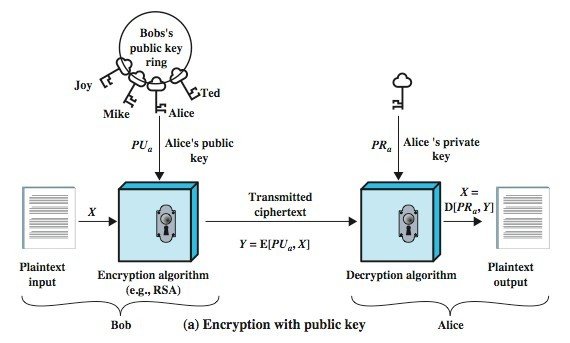
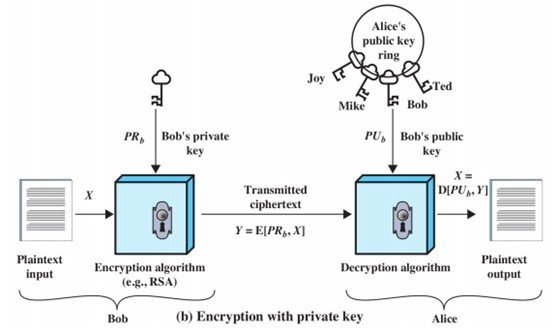
Confidentiality vs Authentication

Use Case

Mail (GPG)
Web (SSL, TLSv1.{1,2,3})
VPN
Ransomware
Secure VOIP
SSH
BitCoin

Breaking RSA Security

n : public key
p , q : private factors of n = p.q
ϕ(n) : Euler’s totient function, here ϕ(n) = (p − 1).(q − 1)
e : public encryption or signature exponent
d : private encryption or signature exponent
e.d ≡ 1 mod ϕ(N) relatioship between public and private
exponent
c ≡ m e mod N : encrypted message
m ≡ c d mod N : decrypted message
Finding d , ϕ(n) or p is enough to crack RSA security

RSA Challenge

RSA-1024 with 309 modulus digits -> 100.000 $

In 2009, to factor a 232-digit number (RSA-768) utilizing hundreds of machines took two years and the researchers estimated that a 1024-bit RSA modulus would take about a thousand times as long. However, it has not been proven that no efficient algorithm exists.

Tools

yafu - Automated integer factorization

https://github.com/DarkenCode/yafu

??SINGLE CORE??

120 digits -> still running after 4 hours...

cado-nfs

https://gforge.inria.fr/scm/?group_id=2065

CADO-NFS is a complete implementation in C/C++ of the Number Field Sieve (NFS) algorithm for factoring integers. It consists in various programs corresponding to all the phases of the algorithm, and a general script that runs them, possibly in parallel over a network of computers.

Input Number	cado-nfs 2.2.0 [hours]
RSA-120	2.2
RSA-130	8.2
RSA-140	30.9
RSA-155	5.8 [days]

Xeon(R) CPU E5-2650 at 2.00GHz, 8 process with 2 thread each

CUDA??

Attacks

MiTM during key exchange
Bad key generation with custom or bugged tools: small factors, common factors, reused factors, weak entropy
GCD for lots of shared public keys
Fermat is p and q are close
ECM (sub-exponential running time algorithm for integer factorization which employs elliptic curves)
Wiener
Bad algorithm applications (Chinese Remainder Theorem)
Known-plaintext attack (only for weak signatures)
Number Field Sieve complex but very parallelizable
Quantum algorithm: O((log N)^3)) !
Side channel (power consumption, social engineering, theft, exploit, ...)

N = p * q = (c + d)(c - d) = c^2 - d^2

N = p * q = (c + d)(c - d) = c^2 - d^2

q < p < 2q, d \le \frac{1}{3} \sqrt[4]{N}

q < p < 2q, d \le \frac{1}{3} \sqrt[4]{N}

Bruteforce n using Fermat or Miller Rabin

with Rust

MillerRabin(n)
If n > 2 and n is even
 return composite.
/* Factor n−1 as 2^s * t where t is odd.  */
s ← 0 
t ← n − 1
while t is even
    s ← s + 1
    t ← t/2
end
/* Done. n − 1 = 2^s * t. */
Choose x∈{1,2,...,n−1} uniformly at random.
Compute each of the numbers x^t,x^(2t),x^(4t),...,x^(2st) = x^(n−1) mod n.
If x^(n−1) !≡ 1  (mod n)
    return composite.
for i = 1,2,...,s
    If x^(2^i *t) ≡ 1  (mod n) and x^(2^(i-1) * t) !≡ ± 1 (mod n)
        return composite.
end
/* Done checking for fake square roots.  */
Return probably prime

If p is an odd prime number, and $p - 1 = 2^s * d$ , with d odd, then for every a prime to p, either $a d \equiv 1 mod p$ , or there exists t such that $0 \leq t < s$ and $a 2 t d \equiv -1 mod p$

Fermat Little Theorem

If p is a prime number, then for any integer a, the number $a * p - a$ is an integer multiple of p. In the notation of modular arithmetic, this is expressed as

a^p \equiv a \pmod p

a^p \equiv a \pmod p

Pick random a that is not divisible by p and see whether the equality holds. If the equality does not hold for a value of a, then p is composite.

Therefore, if the equality does hold for one or more values of a, then we say that p is probably prime.

Disclaimer

yes... again math....

2^{1025} / log(2^{1025}) - 2^{1024} / log(2^{1024}) = ~ 2.53 * 10^{305}

2^{1025} / log(2^{1025}) - 2^{1024} / log(2^{1024}) = ~ 2.53 * 10^{305}

The observabale universe contains about 10⁸⁰ atoms. Assume that we could leverage every single atom as a CPU, and each CPU could enumerate 1.000.000

(I mean: HOLY SHIT!) RSA keys per second.

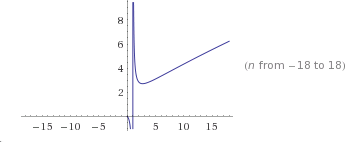
2.53 * 10^{305} microseconds / 10^{80} = 2.53 * 10^{225} ms = 2.53 * 10^{219} s = 7.02 * 10^{215} hours = 8.02169 * 10^{211} years

2.53 * 10^{305} microseconds / 10^{80} = 2.53 * 10^{225} ms = 2.53 * 10^{219} s = 7.02 * 10^{215} hours = 8.02169 * 10^{211} years

The number of primes smaller than an integer n is approximately n/log(n).

Disclaimer

The number of primes smaller than an integer n is approximately n/log(n).

yes... again math....

2^{1025} / log(2^{1025}) - 2^{1024} / log(2^{1024}) = ~ 2.53 * 10^{305}

2^{1025} / log(2^{1025}) - 2^{1024} / log(2^{1024}) = ~ 2.53 * 10^{305}

The observabale universe contains about 10⁸⁰ atoms. Assume that we could leverage every single atom as a CPU, and each CPU could enumerate 1.000.000

(I mean: HOLY SHIT!) RSA keys per second.

2.53 * 10^{305} microseconds / 10^{80} = 2.53 * 10^{225} = 2.53 * 10^{219} s = 7.02 * 10^{215} hours = 8.02169 * 10^{211} years

2.53 * 10^{305} microseconds / 10^{80} = 2.53 * 10^{225} = 2.53 * 10^{219} s = 7.02 * 10^{215} hours = 8.02169 * 10^{211} years

The Big Bang occurred 13.8 * 10⁹ years ago.

~~Bruteforce~~ using Rust

Results

PayPal site have a public key with 617 digits...

Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz

Input Number Length	rsa-rust [seconds]
7	0
13	0
19	97 (*)
29	up to 15 hours (*)
120	impossibru

Duplicate primes using GCD

Factorization is hard but there is way to discover p and q: Greatest Common Divisor

gcd(10, 30) = 10
gcd(100, 144) = 4
gcd(3, 7) = 1

gcd(p, q) = 1

In [11]: %%time
    ...: gmpy2.gcd(1066887566150220425445511836658004853426772855284443812385956279691811153210420393206090450561091324583700261488330797336274357210036391729479838797536785423621,
    ...: 121766994908646736104647201413197886828038168507699680036860497074009374138321196080535007864705376861476504466988251202805423843507051323234232179224638179315321450535646374123533)
    ...: 
CPU times: user 0 ns, sys: 0 ns, total: 0 ns
Wall time: 20.7 µs
Out[11]: mpz(1)

!!!!!!! 20.7 µs !!!!!!!

Duplicate primes using GCD

Select four primes number: a, b, c ,d
Create a public key n1 = a * b
Create another pubic key n2 = c * d

Find the gcd(n1, n2)

Duplicate primes using GCD

Select four primes number: a, b, c ,d
Create a public key n1 = a * b
Create another pubic key n2 = c * d

Find the gcd(n1, n2)

Not Good!! When don't know anything about a, b, c or d!

FUCK YOU RSA!!

Duplicate primes using GCD

Select four primes number: a, b, c ,d
Create a public key n1 = a * b
Create another pubic key n2 = c * d

Find the gcd(n1, n2)

Not Good!! When don't know anything about a, b, c or d!

FUCK YOU RSA!!

What if we use only three prime number to create two publick keys?

Duplicate primes using GCD

Select three primes number: a, b, c
Create a public key n1 = a * b
Create another pubic key n2 = b * c

Find the gcd(n1, n2)

Duplicate primes using GCD

Select three primes number: a, b, c
Create a public key n1 = a * b
Create another pubic key n2 = b * c

Find the gcd(n1, n2)

BINGO!!!!!

The "vulnerablity" is due to faulty random number generators and/or low system entrophy used to generate RSA keys. In 2012 about 0.2% of all REAL public keys seemed to be vulnerable.

In [1]: import gmpy2

In [2]: n1 = 2477 * 577

In [3]: n2 = 577 * 1021

In [4]: %%time
   ...: gmpy2.gcd(n1, n2)
   ...: 
CPU times: user 0 ns, sys: 0 ns, total: 0 ns
Wall time: 8.58 µs
Out[4]: mpz(577)