Algorithms

Who am I?
Eduardo Quintana
Fullstack Developer @Nearsoft
What is an algorithm?

Basically it's a set of well defined rules for solving computational problems.
What are they used for?
Sorting
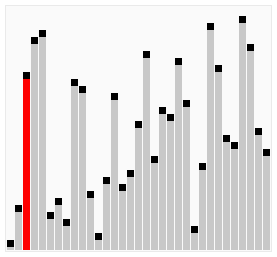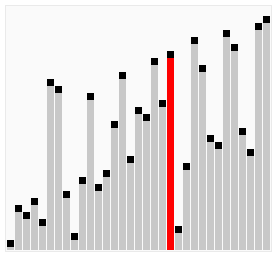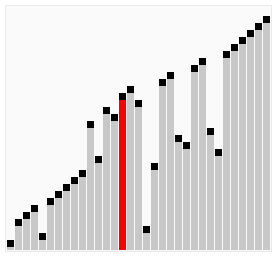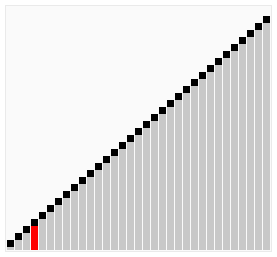
Compute the shortest route
Why study algorithms?
- They are important for all other branches of computer science.
- Play a key role on modern innovation.
- Challenging (i.e. Good for brain)

- Fun
Can we do better?
Asymptotic analysis
Language by which any computer programmers or computer scientists discuss the high level performance of computer algorithms.
- Provides the basic vocabulary for discussing the design and analysis of algorithms.
"The running time of this sorting algorithm is O(n²)"
Big O Notation
The approximate worst-case scenario of doing something
public boolean findItemInList(int toCheck, int[] numbers) {
for (int number : numbers) {
if (toCheck == number) {
return true;
}
}
return false;
}findItemInList(1, [1,2,3]); ???
1 iteration
findItemInList(4, [1,2,3]); ???
3 iterations
worst-case = array.length iterations = n
O(n)
Lower order terms & Constants?
Function: 2n² + 2n
2n² + 2n
Remove constants
Remove lower order terms
n² + n
n² + n
=
=
n²
Ok, but how do I measure the performance of my algorithm?
public boolean findNumber(int numberToFind, int[] numbers) {
for (int i = 0; i < numbers.length; i++) {
if (numbers[i] == numberToFind) {
return true;
}
}
return false;
}For a given array [1,2,3,4,5,6] what would be the running time algorithm of this code?
Assuming the array length is "n" then the running time algorithm of this code is "n" itself.
O(n)
And what about this one?
public boolean findNumber2(int numToFind, int[] firstArray, int[] secondArray) {
//We are assuming both arrays have the same length in this example
for (int i = 0; i < firstArray.length; i++) {
if (firstArray[i] == numToFind) {
return true;
}
}
for (int i = 0; i < secondArray.length; i++) {
if (secondArray[i] == numToFind) {
return true;
}
}
return false;
} We iterate over "n" twice
=
2n
2n
O(n)
public static List<String> allCombinations(int[] items) {
List<String> combinations = new ArrayList<>();
for (int i = 0; i < items.length; i++) {
for (int j = 0; j < items.length; j++) {
combinations.add("(" + items[i] + "," + items[j] + ")");
}
}
return combinations;
}For each "n" iteration we iterate over all the items in "n" again (n x n) = n²
O(n²)
Input:
[1,2,3]
Output:
(1,1), (1,2), (1,3), (2,1), (2,2), ...
Divide & Conquer paradigm
- Divide the problem in smaller subproblems.
- Conquer via recursive calls.
- Combine solutions of subproblems into one for the original problem.
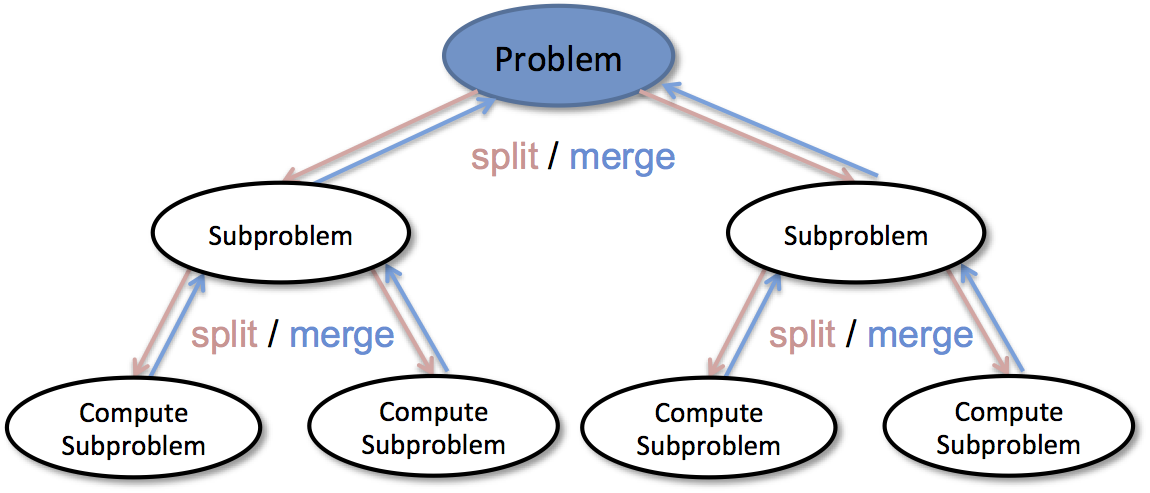
Merge sort analysis
[3,5,1,6,7,0,4]
[3,5,1]
[6,7,0,4]
array of length "n"
[3]
[5,1]
[5]
[1]
[6,7]
[0,4]
[6]
[7]
[0]
[4]
Merge
[1,5]
Merge
[3]
[1,3,5]
, [1,5]
Merge sort code
The problem:
Handle edge cases
sort an array of numbers.
public static int[] mergeSort(int[] list) {
if (list.length <= 1) {
return list;
}
Input:
[3]
Output:
[3]
Divide:
Array into 2 sub problems
public static int[] mergeSort(int[] list) {
/**
* Code from previous slide
*/
int[] first = new int[list.length/2];
int[] second = new int[list.length - first.length];
System.arraycopy(list, 0, first, 0, first.length);
System.arraycopy(list, first.length, second, 0, second.length);Input:
[5,3,6,7,1]
first = [5,3]
second = [6,7,1]
Process subproblems with recursion
public static int[] mergeSort(int[] list) {
/**
* Code from previous slide
*/
mergeSort(first); // [5,3]
mergeSort(second); //[6,7,1]First recursion from first subproblem
public static int[] mergeSort(int[] list) {
/**
* list = [5,3]
* first = [5]
* second = [3]
*/
mergeSort(first); //[5] if we remember edge cases
mergeSort(second); //[3] when array has length 1 return the same list;
//merge([5], [3], [5,3])
merge(first, second, list);
return list;
}Merge solutions
private static void merge(int[] first, int[] second, int[] result) {
//Merges both sorted arrays into the resulting array
int iFirst = 0;
int iSecond = 0;
int j = 0;
//Iterate over the length of both arrays checking which number is larger
while (iFirst < first.length && iSecond < second.length) {
if (first[iFirst] < second[iSecond]) {
result[j] = first[iFirst++];
} else {
result[j] = second[iSecond++];
}
j++;
}
//Copy missing numbers
//arraycopy(Object src, int srcPos,
// Object dest, int destPos, int length)
System.arraycopy(first, iFirst, result, j, first.length - iFirst);
System.arraycopy(second, iSecond, result, j, second.length - iSecond);
}Continue second part recursion
public static int[] mergeSort(int[] list) {
/**
* Code from previous slide
*/
mergeSort(first); // [5,3] => [3,5]
//[6,7,1] => [6] , [7,1] ([7][1]) first recursion [6], [1,7] => [1,6,7]
mergeSort(second);
//merge([3,5], [1,6,7] , [5,3,6,7,1])
merge(first,second,list);
return list;
}Merge sort running time
O(n log2 n)
For each individual problem we execute at most 6 instructions (we are not including edge cases).
- 2 initializations of both arrays
- 4 lines of code of the if
6n operations
We have at most (log2 n + 1)
6n( log2n + 1) = 6n log2 n + 6n
Challenge
Problem:
Determine if two words are anagrams
Anagram:
a type of word play, the result of rearranging the letters of a word or phrase to produce a new word or phrase, using all the original letters the same number of times.
Input:
("mary","army")
Output:
true
Solutions
https://github.com/eddiarnoldo/algorithms
Questions?
