Covering allbases

Edwin Fuquen

edwin@somespider.com

@efuquen

UUIDs in URLs

www.themid.com/culture/what-you-need-to-know-this-week?u=de305d54-75b4-431b-adb2-eb6b9e546013

Deuglify

Remove dashes and

a more efficient encoding.

\frac{128 \text{ bits}}{4 \text{ bits/char}} + 4 \text{ hyphens} = 36 \text{ chars}

\frac{​ 1 2 8 b i t s ​ ​}{​ 4 b i t s / c h a r ​} + 4 h y p h e n s = 36 c h a r s

to

ceil(\frac{128 \text{ bits}}{6 \text{bits/char}}) = 22 \text{ chars}

c e i l (\frac{​ 1 2 8 b i t s ​ ​}{​ 6 b i t s / c h a r ​}) = 22 c h a r s

de305d54-75b4-431b-adb2-eb6b9e546013

3jBdVHW0QxutsutrnlRgEw==

Can we do better?

Do we really need 128 bits?

p(n) \approx 1 - e^{-\frac{n^2}{2m}}

p (n) \approx 1 - e ​ - \frac{​ n ​ 2 ​ ​ ​ ​}{​ 2 m ​} ​ ​

p(n) - probability of collision after n UUIDs generated
m - permutations of the ID (i.e. for UUIDs 2¹²²)
denominator will be fixed for an ID
for a UUID it will equal 2 * 2¹²² which equals 2¹²³

n	probability
68,719,476,736 = 2³⁶	0.0000000000000004 (4 × 10⁻¹⁶)
2,199,023,255,552 = 2⁴¹	0.0000000000004 (4 × 10⁻¹³)
70,368,744,177,664 = 2⁴⁶	0.0000000004 (4 × 10⁻¹⁰)

y = 1 - e^{-x}

y = 1 - e ​ - x ​ ​

x = \frac{n^2}{2m}

x = \frac{​ n ​ 2 ​ ​ ​ ​}{​ 2 m ​}

where

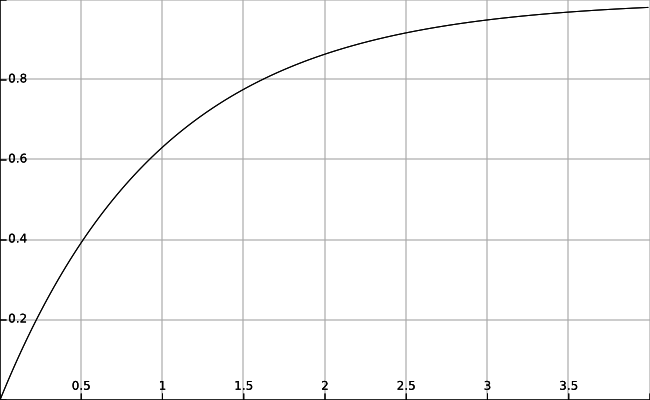
The smaller the x, the lower the probability of collision.

\frac{(2^{36})^{2}}{2^{123}} = \frac{1}{2^{51}}

\frac{​ ( 2 ​ 3 6 ​ ​ ) ​ 2 ​ ​ ​ ​}{​ 2 ​ 1 2 3 ​ ​ ​} = \frac{​ 1 ​ ​}{​ 2 ​ 5 1 ​ ​ ​}

\frac{(2^{42})^2}{2^{123}} = \frac{1}{2^{41}}

\frac{​ ( 2 ​ 4 2 ​ ​ ) ​ 2 ​ ​ ​ ​}{​ 2 ​ 1 2 3 ​ ​ ​} = \frac{​ 1 ​ ​}{​ 2 ​ 4 1 ​ ​ ​}

y = 1 - e^{-x}

y = 1 - e ​ - x ​ ​

x = \frac{n^2}{2m} = \frac{n^2}{2^{123}}

x = \frac{​ n ​ 2 ​ ​ ​ ​}{​ 2 m ​} = \frac{​ n ​ 2 ​ ​ ​ ​}{​ 2 ​ 1 2 3 ​ ​ ​}

where

\frac{(2^{62})^2}{2^{123}} = 2^1

\frac{​ ( 2 ​ 6 2 ​ ​ ) ​ 2 ​ ​ ​ ​}{​ 2 ​ 1 2 3 ​ ​ ​} = 2 ​ 1 ​ ​

1 - e^{-2} = 0.8647

1 - e ​ - 2 ​ ​ = 0.8647

n	x

2^{36}

2 ​ 36 ​ ​

2^{42}

2 ​ 42 ​ ​

2^{62}

2 ​ 62 ​ ​

x	collision
1 / 2³	11.75%
1 / 2⁵	1.55%
1 / 2⁷	0.79%
1 / 2¹¹	0.049%

m = \frac{n^{2}}{x}

m = \frac{​ n ​ 2 ​ ​ ​ ​}{​ x ​}

Assume we're fine with probability of collision of 0.79% after an n of 2^28 (over 268 million) ids.

m = \frac{(2^{28})^2}{\frac{1}{2^7}} = 2^{63} = 63 \, bits

m = \frac{​ ( 2 ​ 2 8 ​ ​ ) ​ 2 ​ ​ ​ ​}{​ \frac{​ 1 ​ ​}{​ 2 ​ 7 ​ ​ ​} ​} = 2 ​ 63 ​ ​ = 63 b i t s

m - size of id needed
n - number of ids generated
x - variable dependent on probability of collision, as defined previously.

ceil(\frac{63 \text{ bits}}{6 \text{bits/char}}) = 11 \text{ chars}

c e i l (\frac{​ 6 3 b i t s ​ ​}{​ 6 b i t s / c h a r ​}) = 11 c h a r s

What do we want?

Correctly randomly generated ids
Encodable and decodable to many formats
To an arbitrarily large size

Most libraries that might have worked failed the last criteria, because ...

Number is 64 bits

Any transformation that goes above 64 bits will would give incorrect results.

https://github.com/efuquen/base62-precision-test

Character Classes


//                 0              15 
var HexChars    = "0123456789abcdef";

//                 0         10        20        30        40        50         61 
var Base62Chars = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ";

Indices reperesent the decimal, or base 10, values of each character in the class.

All the bases can be represented this way and then the same base algorithms can be used to encode and decode.

Encode

//num is a bignum to decode
//chars is a string representing the character class
function encode(num, chars) {
	var len   = chars.length;
	var indices = [];
	do {
		indices.push(num.mod(len));
		num = num.div(len);
	} while (num.gt(0));

	var str = [];
	while (indices.length > 0) {
		str.push(chars[indices.pop()]);
	}
	return str.join("");
}

Let's turn 10 into binary

10\space mod \space2 = 0

10 m o d 2 = 0

indicies = [0];
num = 10 / 2 = 5;

5\space mod \space2\space\space= 1

5 m o d 2 = 1

indices = [0, 1];
num = Math.floor(5/2) = 2

2\space mod \space2 \space\space= 0

2 m o d 2 = 0

1\space mod \space2\space\space = 1

1 m o d 2 = 1

indices = [0, 1, 0];
num = 2/2 = 1;

indices = [0, 1, 0, 1]

str = [1, 0, 1, 0];
str = str.join("") = "1010";

Decode

//str:   string to decode
//chars: string representing character class
function decode(str, chars) {
  str = esrever.reverse(str);
  var num = bignum("0");
  var len = chars.length;
  for (var i = 0; i < str.length; i++) {
    var ch = str[i];
    var chIndex = chars.indexOf(ch);
    var placeNum = bignum.pow(len, i).mul(chIndex);
    num = num.add(placeNum);
  }
  return num;
}

Let's decode base62 D4x7

str = str.reverse() = "7x4D"

i	calc	sum
0	7 * 62⁰	7
1	33 * 62¹	2046
2	4 * 62²	15376
3	39 * 62³	9294792

 0         10        20        30        40        50         61 
"0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"

num = 7 + 2046 + 15376 + 929472 = 9312221

Random

function genRandom(numberOfBytes, chars, rand) {
  var buf = rand(numberOfBytes);
  return encode(bignum.fromBuffer(buf), chars);
}

function random(size, opts) {
  var len   = opts.chars.length;
  var combos = Math.pow(len, size);
  if (combos === Infinity) {
    throw "Too large of a size, can't estimate needed bytes"
  }
  var bits = Math.ceil(log(2, combos));
  var numberOfBytes = Math.ceil(bits / 8);
  return genRandom(numberOfBytes, opts.chars, opts.rand);
}

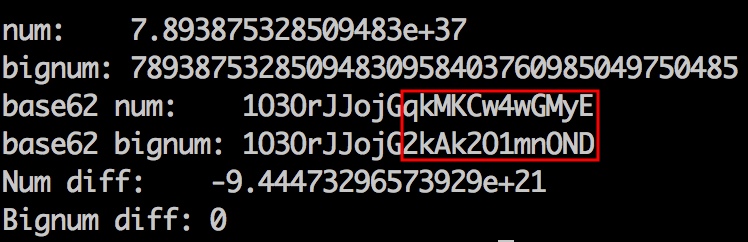
But, isn't a problem here? I'm using Number ...

Number.MAX_VALUE

1.7976931348623157e+308
base62 can't generate more then 171 characters.
Big Decimal? big.js library
But, it doesn't have a log implementation
Two possible solutions:
- Find a good log estimate for large decimals
- Use big.js to detect large combos and break it down to smaller numbers < Number.MAX_VALUE

Conclusions

You can't shove everything into Number
Be careful, encoding/decoding bases one of many issues.
A little rigor can go a long way.
Warn your users, they don't need any extra rope from you. Plenty of other dragons to deal with already.