Life Is A Comonad

Eli Jordan

@eliaskjordan

 http://eli-jordan.github.io

About Me

I am... Lead Developer at Tapad

I am... a Scala Developer

I am not... a Theorist

I am not... an expert in Category Theory

I am... a Functional Programmer

(Co?)Motivation

Game Plan

What is a Comonad?

Zipper as a Metaphor for Comonads

Conway's Game of Life

What is a Comonad?

A comonad is the Dual of a monad 


   trait Monad[F[_]] {
      def unit[A](a: A): F[A]
      def join[A](ffa: F[F[A]]): F[A]
   }

   trait Comonad[F[_]] {
      def counit[A](fa: F[A]): A
      def cojoin[A](fa: F[A]): F[F[A]]
   }

Relation To Monad


   unit  :   A  => F[A]
   counit: F[A] => A

   join  : F[F[A]] => F[A]
   cojoin:    F[A] => F[F[A]]

Rewriting the signatures, the reversal is more apparent

unit: Apple => Box[Apple]

Takes an apple and puts it in a box

counit: Box[Apple] => Apple

Takes an apple in a box, and extracts the apple.

join: Box[Box[Apple]] => Box[Apple]

Takes an apple in a box, in a box, and throws out one of the boxes.

cojoin: Box[Apple] => Box[Box[Apple]]

Takes an apple in a box, and puts it in another box.

unit / counit

In a Monad the unit function takes a pure value, and wraps it in an F structure F[A]

In a Comonad the counit function takes an F structure and extracts a pure value A

join / cojoin

In a Monad the join function takes two layers of F structure F[F[A]] and collapses it into one layer F[A]

In a Comonad the cojoin function takes one layer of F structure F[A] and duplicates it F[F[A]]

Thats the definition...

But, how do

      comonads behave?

... enter the Zipper

Zipper as a Metaphor for Comonads

Zipper

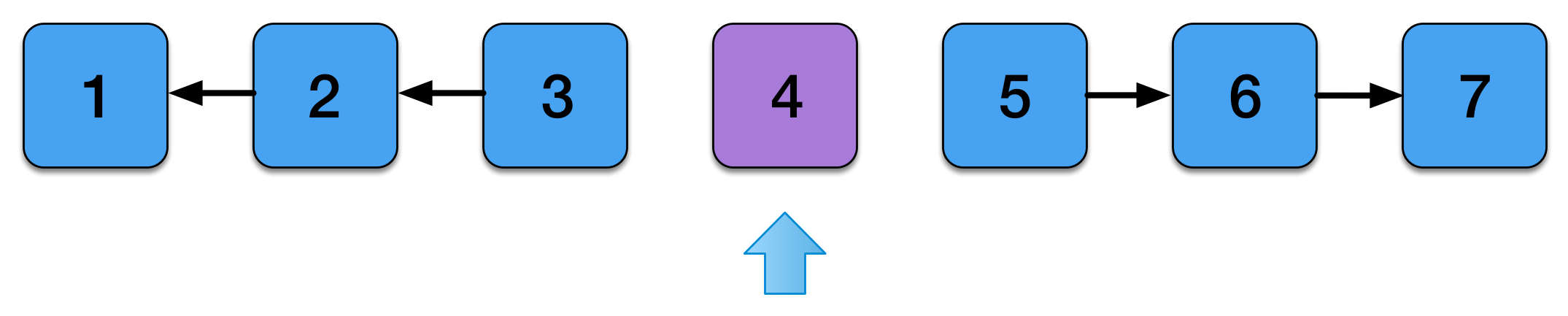
Moving Left

Moving Right

The Code

case class StreamZipper[A](
   left: Stream[A], focus: A, right: Stream[A]) {
    
   def moveLeft: StreamZipper[A] =
       new StreamZipper[A](
          left.tail, left.head, focus #:: right)

    def moveRight: StreamZipper[A] =
       new StreamZipper[A](
          focus #:: left, right.head, right.tail)
 }

Whats that got to do with comonads?

 

  • counit extracts an A from an F[A]
     
  • If F == StreamZipper, this is trivial
    we just access the focus element.

implicit object ZipperComonad extends 
   Comonad[StreamZipper] {

  def counit[A](fa: StreamZipper[A]): A = 
    fa.focus

  // ...
}

So, we have half a comonad...

What about the other half a.k.a cojoin?

 

  • We need to generate a StreamZipper[StreamZipper[A]]
     
  • The key insight required to define cojoin, is that we want to
    • Duplicate the original zipper, but  with the focus shifted.
    • There should be a duplicate with the focus set on every element in the original zipper.
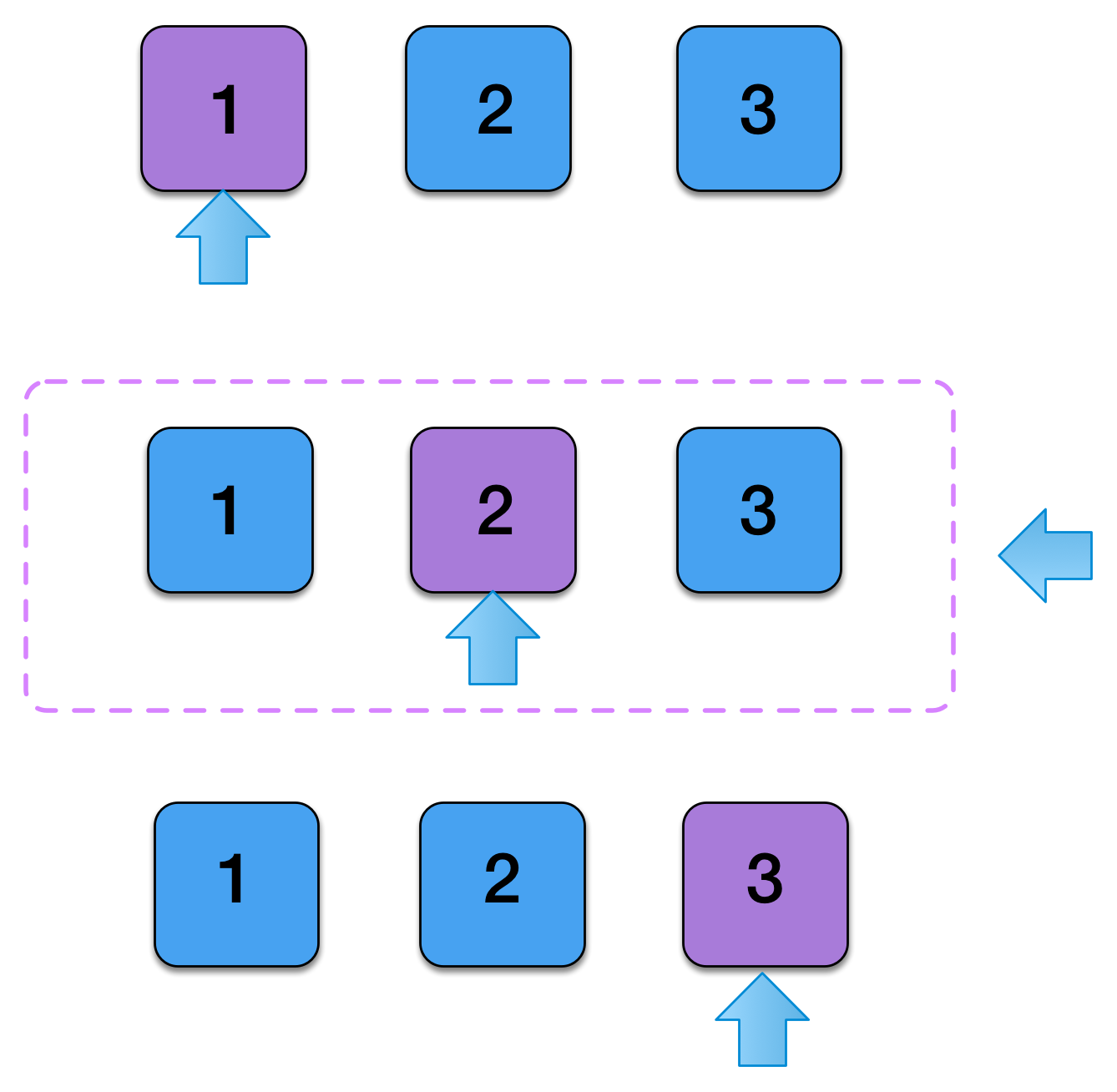
case class StreamZipper[A](
  left: Stream[A], focus: A, right: Stream[A]) {
  // ... 
  
  // A stream of zippers, with the focus set to each 
  // element on the left
  private lazy val lefts: Stream[StreamZipper[A]] =
    Stream.iterate(this)(_.moveLeft)
      .tail.zip(left).map(_._1)

  // A stream of zippers, with the focus set to each 
  // element on the right
  private lazy val rights: Stream[StreamZipper[A]] =
    Stream.iterate(this)(_.moveRight)
      .tail.zip(right).map(_._1)
    
  lazy val cojoin: StreamZipper[StreamZipper[A]] =
    new StreamZipper[StreamZipper[A]](lefts, this, rights)
}

implicit object ZipperComonad extends 
  Comonad[StreamZipper] {
  
  def counit[A](fa: StreamZipper[A]): A = 
    fa.focus

  def cojoin[A](fa: StreamZipper[A]): 
    StreamZipper[StreamZipper[A]] = fa.cojoin
}

Now, the comonad instance is trivial

Recap

 

  • A Comonad is the dual of a Monad
     
  • It has two operations counit and cojoin
     
  • A zipper is an example of a Comonad
     
  • But, Monads also have the flatMap operation
     
  • How do we define coflatMap?

We Derive It

But, lets first look at our definitions again

trait Monad[F[_]] {
  def unit[A](a: A): F[A]
  def join[A](ffa: F[F[A]]): F[A]
  
  def flatMap[A, B](fa: F[A])(f: A => F[B])
      (implicit F: Functor[F]): F[B] = ???
}
trait Comonad[F[_]] {
  def counit[A](fa: F[A]): A
  def cojoin[A](fa: F[A]): F[F[A]]

  def coflatMap[A, B](fa: F[A])(f: F[A] => B)
      (implicit F: Functor[F]): F[B] = ???
}
trait Monad[F[_]] {
  def unit[A](a: A): F[A]
  def join[A](ffa: F[F[A]]): F[A]
  
  def flatMap[A, B](fa: F[A])(f: A => F[B])(...): F[B] = 
    join(fa.map(f))
}
trait Comonad[F[_]] {
  def counit[A](fa: F[A]): A
  def cojoin[A](fa: F[A]): F[F[A]]

  def coflatMap[A, B](fa: F[A])(f: F[A] => B)(...): F[B] =
    cojoin(fa).map(f)
}

A Mental Model of coflatMap

  • The function passed to coflatMap can be thought of as a local computation.
     
  • We first cojoin, to get a view of the structure from all perspectives.
     
  • We then use map to apply a local computation from every perspective.

cojoin(                ) = 

cojoin(fa).map(f)

cojoin(fa).map(f) 

f: StreamZipper[Int] => Int

map(                )

=

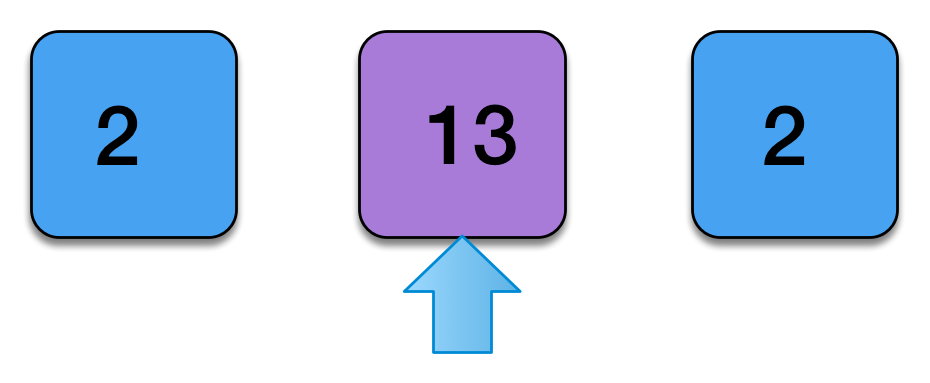
coflatMap extends a local computation into a global context

Sliding Average

def avg(a: StreamZipper[Int]): Double = {
   val left = a.moveLeft.focus
   val current = a.focus
   val right = a.moveRight.focus
   (left + current + right) / 3d
}

// Note: The StreamZipper constructor reverses 
//       the first list.
StreamZipper(List(1, 2, 3), 4, List(5, 6, 7))
   .coflatMap(avg).toList

// List(1.33.., 2.0, 3.0, 4.0, 5.0, 6.0, 6.66..)

Conway's
Game of Life

What is it?

  • A two-dimensional grid of evolving cells that are alive or dead.
     
  • At each evolution, the next state of a cell is determined by the state of its neighbours.

The Rules

 

  1. Current = alive and < 2 neighbours alive       => dead (underpopulation)
     
  2. Current = alive and 2 or 3 neighbours alive  => alive
     
  3. Current = alive and > 3 neighbours alive       => dead  (over population)
     
  4. Current = dead  and 3 neighbours alive         => alive (reproduction)

Modelling The Solution

  • The next state of a cell is determined by its local neighbourhood
     
  • The rules need to be extended from a local definition to apply globally.
     
  • Does that remind you of coflatMap? (it should!)
     
  • We will use this alignment, and an extension of the StreamZipper to implement the Game Of Life 
case class Grid[A](
     value: StreamZipper[StreamZipper[A]]) {

  def moveUp: Grid[A] = 
    Grid(value.moveLeft)

  def moveDown: Grid[A] = 
    Grid(value.moveRight)

  def moveLeft: Grid[A] = 
    Grid(value.map(_.moveLeft))

  def moveRight: Grid[A] = 
    Grid(value.map(_.moveRight))

  def counit: A = 
    value.counit.counit

  def cojoin: Grid[Grid[A]] = ??? // TODO
}

Extending The Zipper into 2 Dimensions

case class Grid[A](
     value: StreamZipper[StreamZipper[A]]) {

  def cojoin: Grid[Grid[A]] = 
    Grid(layer(layer(value))).map(Grid.apply)

  // Notice that the implementation is very similar to 
  // what we had in our original zipper except that we 
  // need to make use of the 'map' function in the iteration.
  private def layer[X](u: StreamZipper[StreamZipper[X]]): 
         StreamZipper[StreamZipper[StreamZipper[X]]] = {
      
    val lefts = Stream.iterate(u)(ssx => ssx.map(_.moveLeft))
              .tail.zip(u.left).map(_._1)

    val rights = Stream.iterate(u)(ssx => ssx.map(_.moveRight))
              .tail.zip(u.right).map(_._1)

    StreamZipper(lefts, u, rights)
  }
}

Using the same derivation of coflatMap we get

case class Grid[A](...) {
  // ...
  def coflatMap[B](f: Grid[A] => B): Grid[B]
}

The function f is what we need to implement.
It will define the rules of the game.

def conway(grid: Grid[Boolean]): Boolean = ???
def conway(grid: Grid[Boolean]): Boolean = {
  val liveCount = neighbours(grid).count(identity)

  grid.counit match {
   // under population
   case true if liveCount < 2 => false
   // thriving
   case true if liveCount == 2 || liveCount == 3 => true
   // over population
   case true if liveCount > 3 => false
   // reproduction
   case false if liveCount == 3 => true
  }
}

Now, translating the rules is very simple...

def neighbours[A](grid: Grid[A]): List[A] = 
  List(
    grid.moveUp,
    grid.moveDown,
    grid.moveLeft,
    grid.moveRight,
    grid.moveUp.moveLeft,
    grid.moveUp.moveRight,
    grid.moveDown.moveLeft,
    grid.moveDown.moveRight
  ).map(_.counit)

For completeness

Run Our Game!

Review

  • We explored the definition of a Comonad
     
  • Provided an intuition for Comonads, using the Zipper
     
  • Demonstrated the use of a Comonad to solve a programming problem, but implementing
    Conway's Game Of Life

References

We're Hiring

https://www.tapad.com/careers/open-roles

Questions?

Appendix

Comonad Laws

// Left identity
wa.cojoin.counit <-> wa

// Right identity
wa.coflatMap(_.counit) <-> wa 

// Associativity  
wa.cojoin.cojoin <-> wa.coflatMap(_.cojoin)
Made with Slides.com