Games AI
0: Intro
ABout & not about
ABout & not about
- Not about Neuronal Networks
- Not about Mathematics
- Reinforcement Learning
ABout & not about
- Not about Neuronal Networks
- Not about Mathematics
- Reinforcement Learning
- But were still doing it
- But were still doing it
- Were creating AI that learns a Game
- Were not creating AI to be in a Game
- Important for reasoning
- Unavoidable for certain problems
About me
About me



About me





About me





Course Overview
Chapters
Chapters
0
RL
Intro
- General Infos
- Base Principle
- Markov Decision Process
Chapters
1
Dynamic
Programming
0
RL
Intro
- Markov Decision Process
- General Policy Iteration
- Asuming perfect Conditions
- Learning
- On Policy
- Model Based
Chapters
2
Monte
Carlo
1
Dynamic
Programming
0
RL
Intro
- Sampling Theory
- Monte Carlo Variants
- Learning
- Off Policy
- Model Free
Chapters
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
0
RL
Intro
- Merging Chapter 1 & 2
- SARSA / Q-Learning
- Learning
- Online
- Immediately
Chapters
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
0
RL
Intro
- Eliminate memory limitations
- Improve on Chapter 3
- Learn Generalisation
- Pytorch Intro
Chapters
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
5
Deep
QLearning
0
RL
Intro
- Neuronal Networks
- Improve RL Loop
- Improve NN Loop
Chapters
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
5
Deep
QLearning
0
RL
Intro
6
Policy
Gradient
Portfolio
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
5
Deep
QLearning
0
RL
Intro
6
Policy
Gradient
Portfolio
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
5
Deep
QLearning
0
RL
Intro
6
Policy
Gradient
Portfolio
2
Monte
Carlo
1
Dynamic
Programming
3
Temporal
Difference
4
Function
Approximation
5
Deep
QLearning
PORTFOLIO
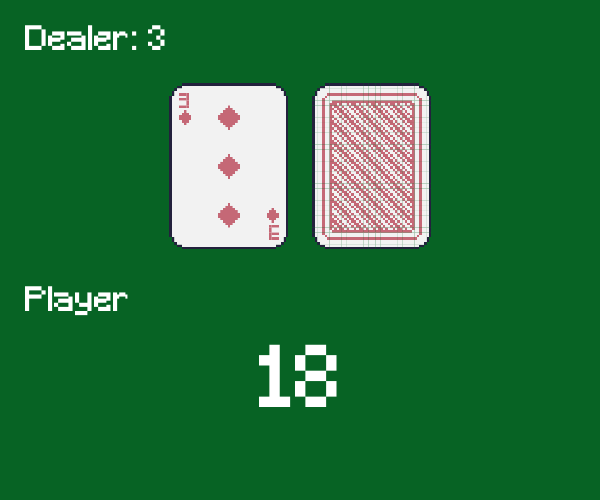
2
Monte
Carlo
Blackjack
1
Dynamic
Programming
Icy Lake

3
Temporal
Difference
Taxi

4
Function
Approximation
Mountain Car
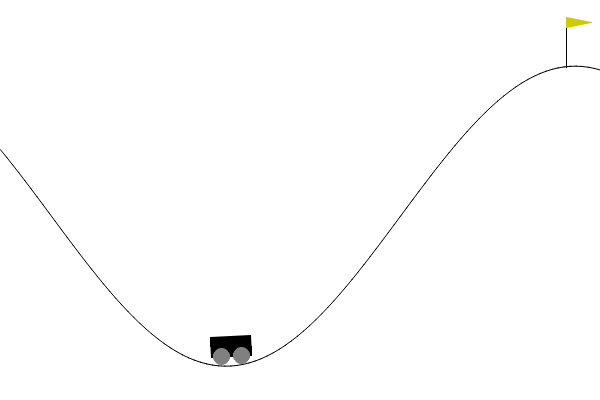
5
Deep
QLearning
Atari 2600

Rating

2
Monte
Carlo
Blackjack
1
Dynamic
Programming
Icy Lake

3
Temporal
Difference
Taxi

4
Function
Approximation
Mountain Car

5
Deep
QLearning
Atari 2600

20%
20%
20%
20%
20%
5
5
5
5
5
Rating

2
Monte
Carlo
Blackjack
1
Dynamic
Programming
Icy Lake

3
Temporal
Difference
Taxi

4
Function
Approximation
Mountain Car

5
Deep
QLearning
Atari 2600

20%
20%
20%
20%
20%
5
5
5
5
5
Note 5
Note 4
Note 3
Note 2
Note 1
Rating

2
Monte
Carlo
Blackjack
1
Dynamic
Programming
Icy Lake

3
Temporal
Difference
Taxi

4
Function
Approximation
Mountain Car

5
Deep
QLearning
Atari 2600

20%
20%
20%
20%
20%
5
5
5
5
5
Note 5
Note 4
Note 3
Note 2
Note 1
00 - 04
05 - 10
11 - 15
16 - 20
21 - 25
Literature
The Book
The Book

The Book

- "Bible" of RL
- Very detailed
- PDF is for free
A Video Playlist
A VIDEO PLAYLIST
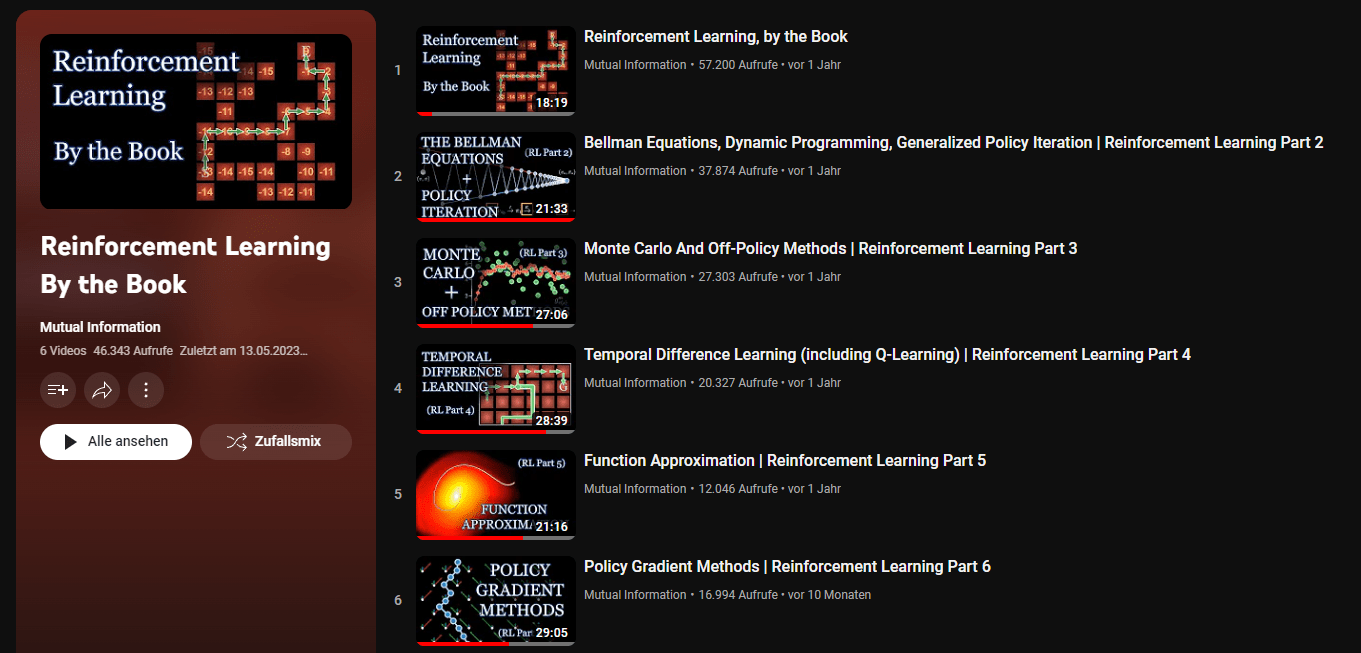
A VIDEO PLAYLIST
- Fast & compressed
- Beatiful visualisations
- Linked Github Repo

Examples

https://openai.com/research/openai-five
Dota 2
https://deepmind.google/technologies/alphago/
AlphaGo

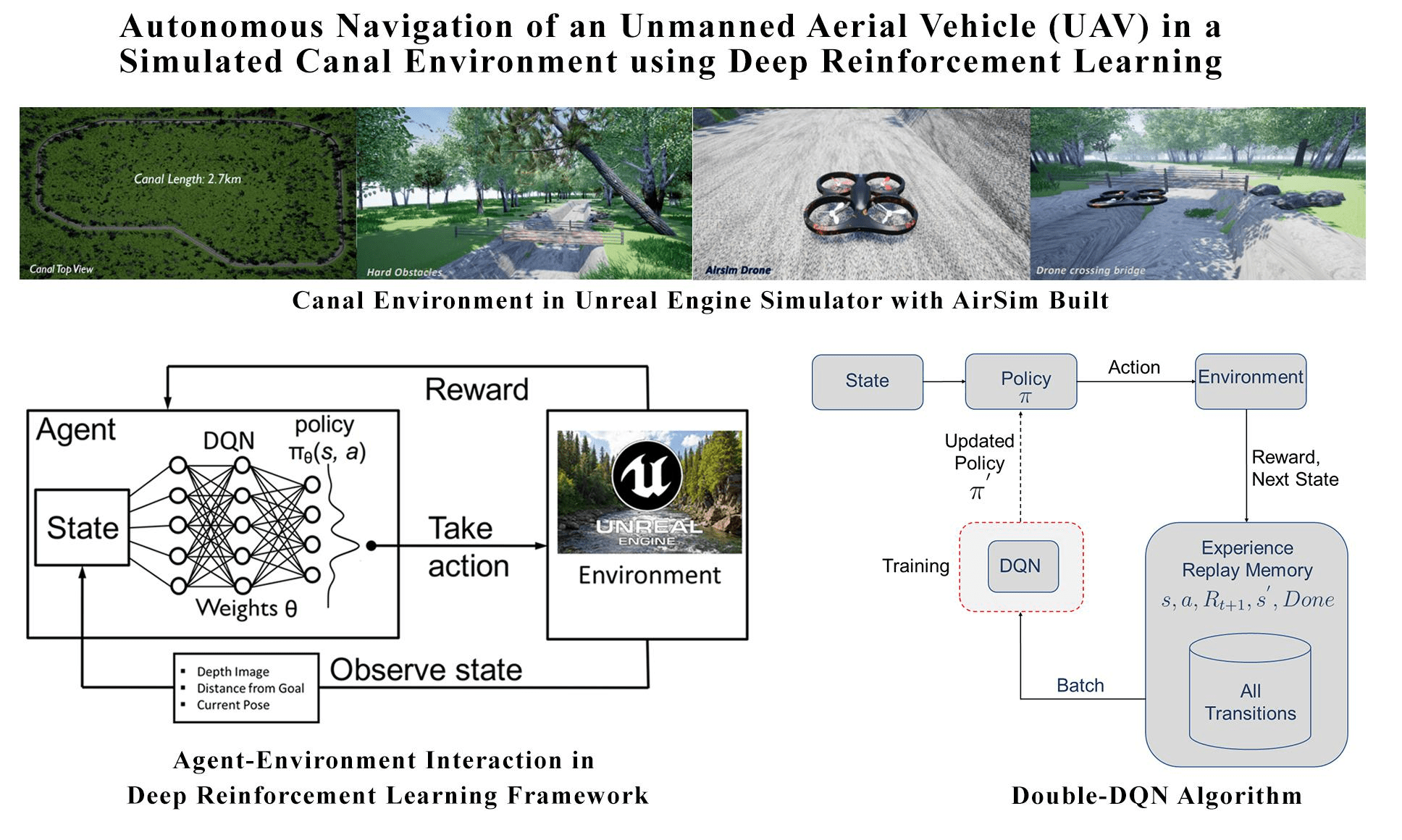
https://arxiv.org/pdf/1801.05086.pdf
Autonomous UAV Navigation
https://www.roboticsproceedings.org/rss05/p27.pdf
LITTLEDOG BOSTON DYNAMICS

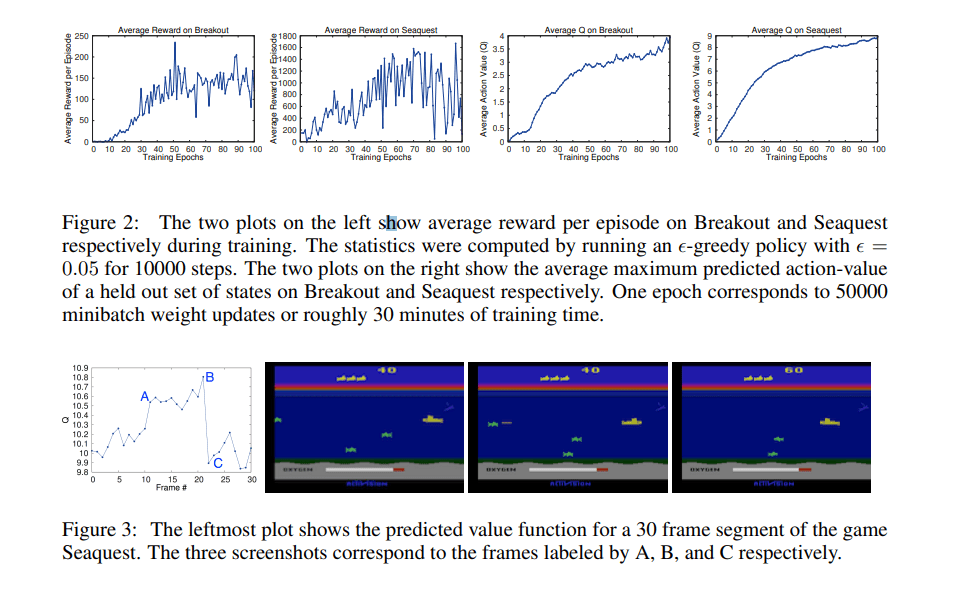
https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf
PLAYING ATARI
Tools
Gymnasium
PyTorch

Python + JUPYTER
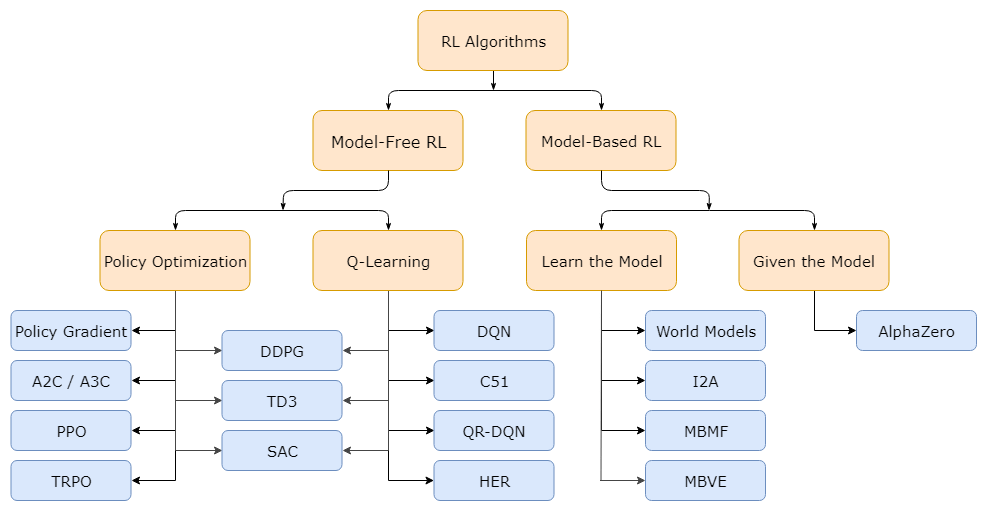
Reinforcment Learning
WHat is RL
WHat is RL
Supervised
Unsupervised
Machine Learning
Reinforcement
- Labeled Data
- Regression
- Classification
- Unlabeled Data
- Clustering
- Embedding
- Semisupervised
- Interactive
WHat is RL
Supervised
Unsupervised
Machine Learning
Reinforcement
- Labeled Data
- Regression
- Classification
- Unlabeled Data
- Clustering
- Embedding
- Semisupervised
- Interactive
WHat is RL
Supervised
Unsupervised
Machine Learning
Reinforcement
- Labeled Data
- Regression
- Classification
- Unlabeled Data
- Clustering
- Embedding
- Semisupervised
- Interactive
WHat is RL
Supervised
Unsupervised
Machine Learning
Reinforcement
- Labeled Data
- Regression
- Classification
- Unlabeled Data
- Clustering
- Embedding
- Semisupervised
- Interactive
WHat is RL
Supervised
Unsupervised
Machine Learning
Reinforcement
PRINCIPLE
PRINCIPLE
Agent
PRINCIPLE
Agent
Environment
PRINCIPLE
Agent
Environment
Time
Action
PRINCIPLE
Agent
Environment
Time
State
Action
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
Trail:
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:
PRINCIPLE
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:

Finite Markov Decision process
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:

Finite Markov Decision process
Agent
Environment


Markov What?
Markov Property
The probability of transitioning to the next state depends only on the current state, not on the sequence of events that preceded it.
MDP
Finite Markov Decision process
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:

Finite Markov Decision process
Agent
Environment
Time
State
Action
Reward
Trail:
Goal:
State Value:
Action Value:

Rewards & Objective
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
The actual Outcome for t
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
The actual Outcome for t

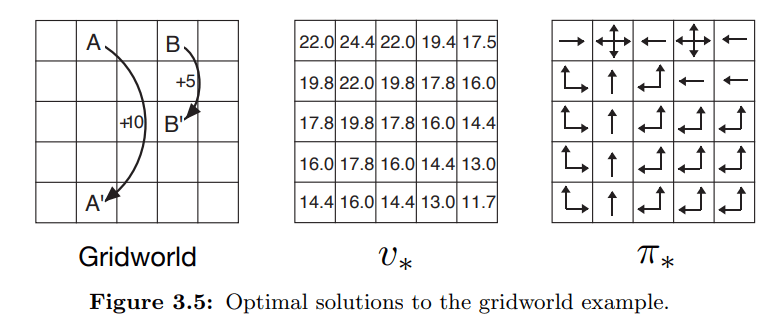
REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
What is the expected Outcome at the given state
The actual Outcome for t


REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
What is the expected Outcome at the given state
What is the expected Outcome at the given state taking an action
The actual Outcome for t


REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:


REWARDS & OBJECTIVE
Goal:
State Value:
Action Value:
REWARDS & OBJECTIVE & Policies
Goal:
State Value:
Action Value:
Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy:
REWARDS & OBJECTIVE & POLICIES
Goal:
State Value:
Action Value:
Policy:
optimal Policy: