Estimación de parámetros cosmológicos con CosmoSIS

Favio Vázquez
Cosmólogo y Data Scientist


@faviovaz





7 de abril 2017
Encuestas
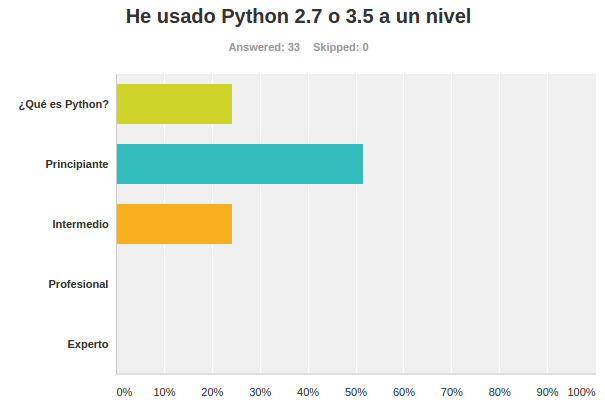
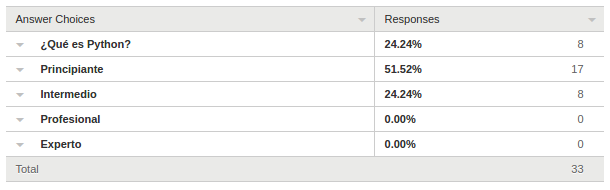
Encuestas
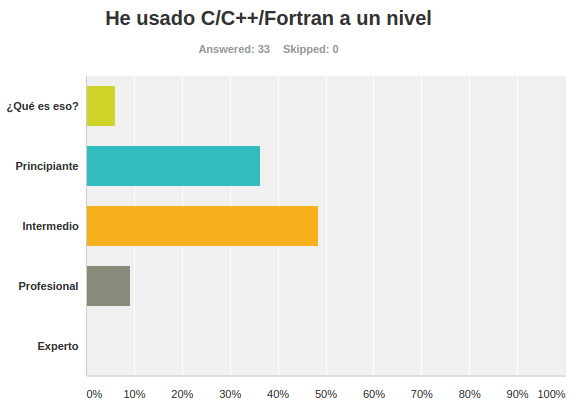
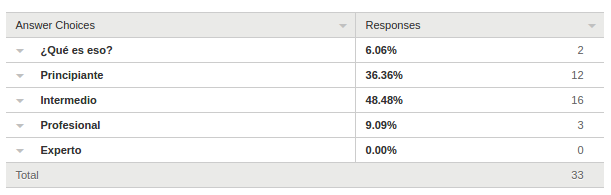
Encuestas
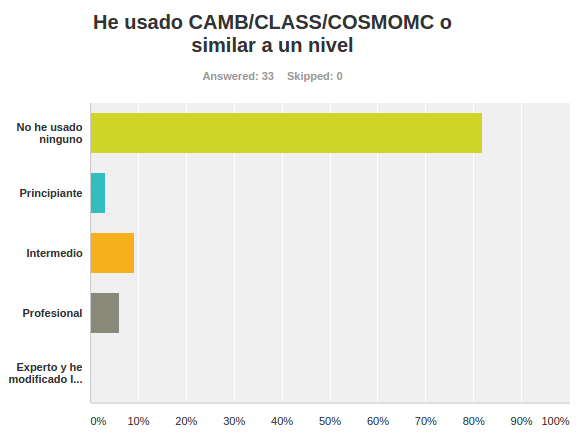
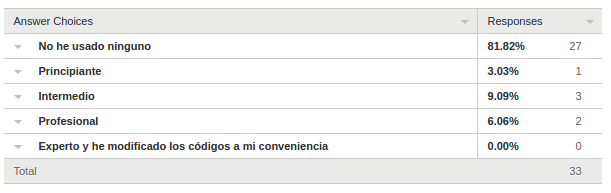
Encuestas
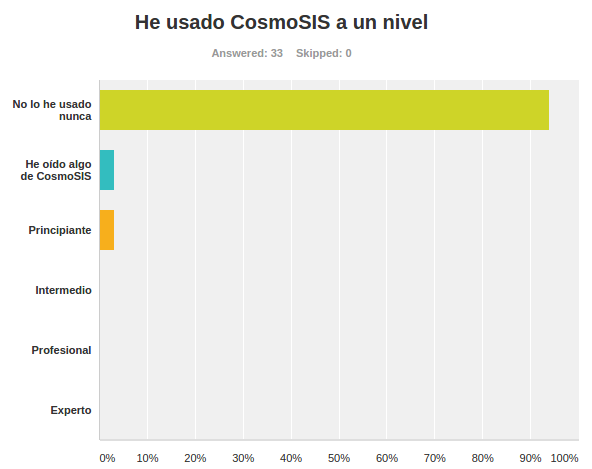
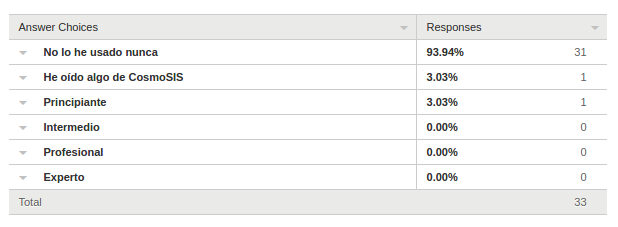
Instalación
- Instala Docker (paso uno de https://docs.docker.com/docker-for-mac/ para OSX) desde www.docker.com
- Arranca Docker siguiendo las instrucciones del sitio. No hace falta leer los tutoriales.
- Descarga esta herramienta corriendo:
- Con el comando cd muévete al nuevo directorio de cosmosis-docker y corre:
git clone https://bitbucket.org/joezuntz/cosmosis-dockersudo ./get-cosmosis-and-vm ./cosmosisInstalación
- Ya que la descarga y el proceso de instalación esté completo, corre:
- Para obtener la versión de dasarrollo que tiene algunos bugs corregidos y los últimos updates corre el comando:
- La primera vez que hagas todos estos pasos debes correr make
update-cosmosis --developsudo ./start-cosmosis-vm ./cosmosisEn el futuro solo hace falta que corras:
sudo ./start-cosmosis-vm ./cosmosisResumen

¿Qué es CosmoSIS?
Estimación de parámetros cosmológicos
Estructura de CosmoSIS
Ejemplos y demos
Retos en cosmología de precisión
Retos en cosmología de precisión

Muchos observables, correlacionados algunos:
CMB, lensing, clusters de galaxias,supernovas
Diferentes modelos teóricos:
Ajustes de curvas de supernovas, modelos de bias para galaxias
Diferentes parámetros y sistemática en cada modelo:
¿Cómo samplear sobre cada uno de ellos?
Posteriors y Likelihoods complicados, a veces multimodales:
La forma de samplear puede impactar en los resultados
Retos en cosmología de precisión

Grandes colaboraciones, de cientos de personas (DES, DESI, PLANCK, etc.):
¿Cómo rastrear contribuciones, asegurar reproducibilidad y consistencia?
¿Cómo usar la cantidad de códigos existentes, así como datos, sin pasarnos años intentando descifrarlos (a veces toda una maestría o doctorado)?
¿Cómo saber qué tipo de código usar, y que lenguaje de programación aprender para poder realizar una investigación?

¿Qué es?
CosmoSIS fue diseñado para intentar solucionar cada uno de estos problemas.
CosmoSIS es un código para la estimación de parámetros cosmológicos.
Es un framework para estructurar estimaciones a parámetros cosmológicos, en una manera que facilita la reusbilidad, depuración, verificabilidad y compartir código en la forma de módulos de cálculo.
COSMOlogy Survey Inference System

¿Qué es?
Consolida y conecta los códigos existentes para predecir observables cósmicos, y hace mucho más accesible el mapeo de likelihoods experimentales con un rango de diferentes técnicas.







Estimación de parámetros cosmológicos
Debido a la precisión de los experimentos actuales y futuros, muy rara vez podemos usar soluciones analíticas para predecir observables
Los cálculos cada vez se hacen más difíciles
Ej: Estudios de CMB requieren de códigos de Boltzman, como CAMB
Estimación de parámetros cosmológicos

Parámetos "Nuisance" (estorbo, molestia)
Necesarios para describir efectos físicos específicos de los datos, foregrounds y la sistemática de los instrumentos
Ej: El likelihood de Planck 2015 puede tener hasta 16 parámetros nuisance:

Estimación de parámetros cosmológicos

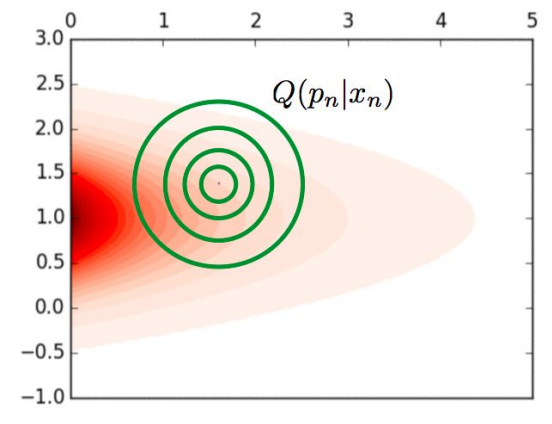
Espacio de parámetros
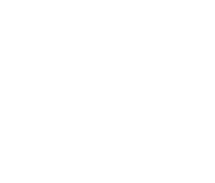
La inferencia se hace en un espacio de parámetros multidimensional que puede ser altamente no gausiano.
Dado un modelo M, ¿cuál región del espacio de parámetros se ajusta a los datos?
Las probabilidades en este espacio son funciones de muchas variables
La intuición deja de servir mientras la dimensión aumenta
Estimación de parámetros cosmológicos

¿Cómo reportar un parámetro?
El mejor ajuste
Barras de error


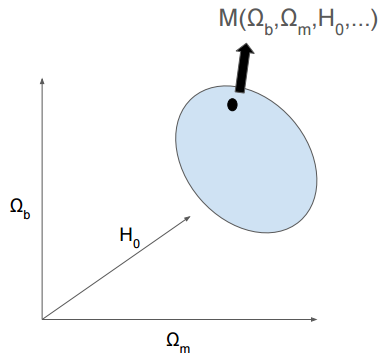
Una medición verdadera de un parámetro es una función de probabilidad que muestra su función de distribución de probabilidad posterior
Comúnmente resume distribuciones usando solo la media y la variancia
La descripción solo es completa
cuando la distribución es gausiana
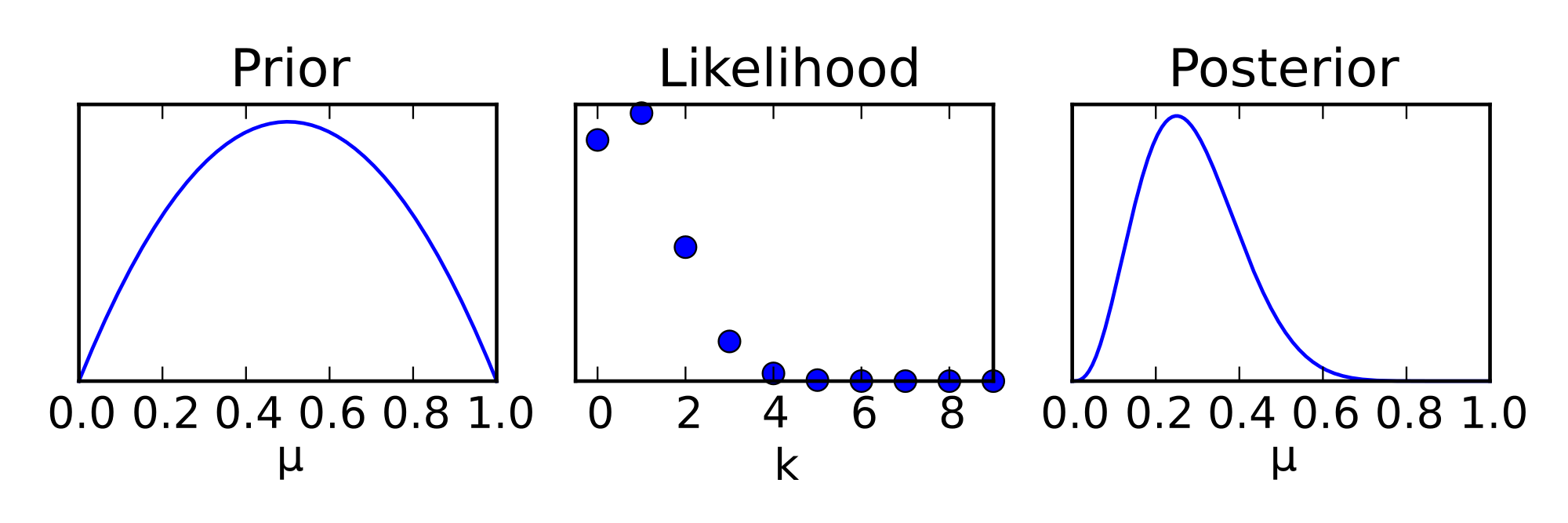
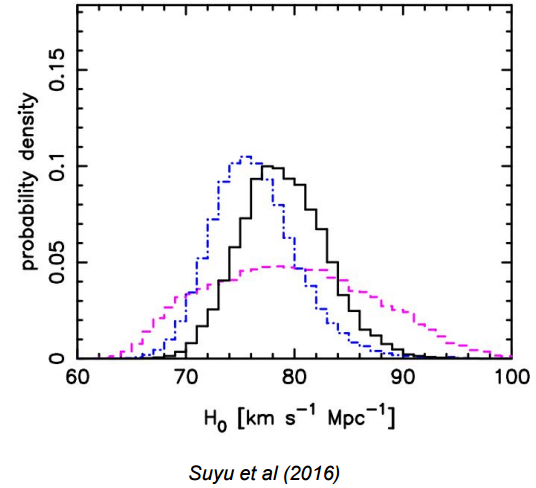
Teorema de Bayes
Distribución posterior para los parámetros (lo que queremos)
Evidencia (constante de normalización)
Likelihood: Debe determinarse esta función del modelo y los datos a partir de la física del problema
Prior: Información previa

Allen B. Downey

David Barber

Hobson, Liddle, et al.


Más información
Estimación de parámetros cosmológicos

Restringir parámetros cosmológicos dados unos datos
Paso 1: En un punto dado del espacio de parámetros genera una predicción
Paso 2: Computa una probabilidad para los datos dada esa predicción
Paso 3: Usa el teorema de Bayes para obtener el posterior dado un prior
Paso 4: El sampler propone el siguiente punto en el espacio de parámetros para evaluar el likelihood





Estructura
Pipeline: Secuencia de cálculos que computan la probabilidad conjunta a partir de una serie de parámetros
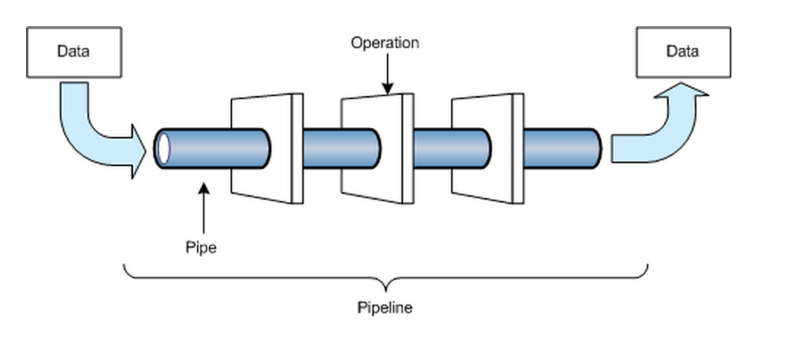
[pipeline]
modules = consistency camb halofit
Estructura
Modulo: Los "pipes" individuales en el pipeline. Cada uno realiza un paso separado el cálculo. Algunos hacen física, otros interpolación, y al final algunos general likelihoods
[camb]
file = cosmosis-standard-library/boltzmann/camb/camb.so
mode=all
lmax=2500
feedback=2Muchos módulos vienen incluidos en la librería estándar de cosmoSIS y el usuario puede crear nuevos

Estructura
Módulos en la librería estándar
background
- distances (2015) Output cosmological distance measures for dynamical dark energy
bias
-
clerkin (1) Compute galaxy bias as function of k, z for 3-parameter Clerkin et al 2014 model
-
constant_bias (1) Apply a galaxy bias constant with k and z.
-
no_bias (1) Generate galaxy power P(k) as though galaxies were unbiased DM tracers
intrinsic_alignments
-
linear_alignments (1.0) Compute the terms P_II and P_GI which go into intrinsic aligment calculations

Estructura
Módulos en la librería estándar
boltzmann
-
camb (Jan15) Boltzmann and background integrator for BG, CMB, and matter power
-
camb (Nov13) Boltzmann and background integrator for BG, CMB, and matter power (Note some settings in this module may not be consistent with other modules e.g. the Planck likelihood. Camb 2015 is recommended in this case)
-
class (2.4.1) Boltzmann and background integrator for BG, CMB, matter power, and more
-
extrapolate (1.0) Simple log-linear extrapolation of P(k) to high k
-
Halofit (Camb-Oct-09) Compute non-linear matter power spectrum
-
Halofit_Takahashi (Camb-Nov-13) Compute non-linear matter power spectrum
-
isitgr-camb (1.1) Modified version of CAMB to implement phenomenological modified gravity models
-
mgcamb (Feb14) Modified Gravity Boltzmann and background integrator for BG, CMB, and matter power
-
sigma_r (1.0) Compute anisotropy dispersion sigma(R,z)

Estructura
Módulos en la librería estándar
likelihood
-
2pt (1) Generic 2-point measurement Gaussian likelihood
-
WiggleZBao (1401.0358v2) Compute the likelihood of the supplied expansion history against WiggleZ BAO data
-
BBN (PDG13) Simple prior on Omega_b h^2 from light element abundances
-
BICEP2 (20140314) Compute the likelihood of the supplied CMB power spectra
-
BOSS (1303.4486) Compute the likelihood of supplied fsigma8(z=0.57), H(z=0.57), D_a(z=0.57), omegamh2, bsigma8(z=0.57)
-
Extreme_Value_Statistics (1.0) PDF of the maximum cluster mass given cosmological parameters
-
Cluster_mass (1.0) Likelihood of z=1.59 Cluster mass from Santos et al. 2011
-
fgas (2014) Likelihood of galaxy cluster gas-mass fractions
-
JulloLikelihood (2012) Likelihood of Jullo et al (2012) measurements of a galaxy bias sample
-
planck (1.0) Likelihood function of CMB from Planck
-
planck2015 (2) Likelihood function of CMB from Planck 2015 data
-
planck2015_simple (2) Simplified Likelihood function of CMB from Planck 2015 TT TE EE data
-
Riess11 (2011) Likelihood of hubble parameter H0 from Riess et al supernova sample
-
shear_xi (1.0) Compute the likelihood of a tomographic shear correlation function data set
-
planck_sz (1.0) Prior on sigma_8 * Omega_M ** 0.3 from Planck SZ cluster counts
-
wmap (4.1) Likelihood function of CMB from WMAP
-
wmap (5) Likelihood function of CMB from WMAP
-
wmap_shift (1.0) Massively simplified WMAP9 likelihood reduced to just shift parameter

Estructura
Módulos en la librería estándar
- mass_function
- number_density
- shear
- strong lensing
- structure
- supernova
- utility
60 módulos y muchos más en creación

Estructura
Value File: Archivo con los nombres y valores, o rangos de valores, para tus parámetros.
[cosmological_parameters]
;physical densities (better suited for CMB only likelihood)
ommh2 = 0.12 0.138 0.19 ;physical density fraction for matter today
ombh2 = 0.005 0.0191 0.03 ;physical density fraction for baryon today
h0 = 0.6 0.67 0.8
;inflation Parameters
n_s = 0.92 0.962 1.0 ;scalar spectral index
A_s = 2.0e-9 2.198e-9 2.3e-9 ;scalar spectrum primordial amplitude
k_s = 0.05 ;Power spectrum pivot scale
;reionization
tau = 0.08 ;reionization optical depth
;spatial curvature
omega_k = 0.0
;dark energy equation of state
w = -1.0 ;equation of state of dark energy
wa = 0.0 ;equation of state of dark energy (redshift dependency)
;inflation Parameters
n_run = 0.0 ;running of scalar spectrum
[planck]
a_planck = 1.0
Estructura
Sampler: Código que escoge un conjunto de parámetros y a partir de los cuales generará el likelihood. Coloca el valor inicial de cada parámetro en el datablock.
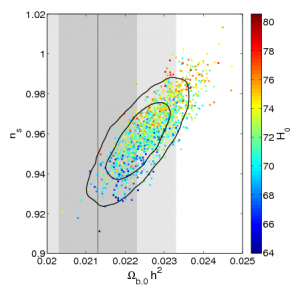

Estructura
Samplers en la librería estándar
Simple:
- test sampler Evaluate a single parameter set
- list sampler Re-run existing chain samples
Classic:
- metropolis sampler Classic Metropolis-Hastings sampling
- importance sampler Importance sampling
- fisher sampler Fisher Matrices
Max-Like:
- maxlike sampler Find the maximum likelihood using various methods in scipy
- gridmax sampler Naive grid maximum-posterior
Ensemble:
- emcee sampler Ensemble walker sampling
- kombine sampler Clustered KDE
- multinest sampler Nested sampling
- pmc sampler Adaptive Importance Sampling
Grid:
- grid sampler Regular posterior grid
- snake sampler Intelligent Grid exploration

Estructura
DataBlock: Mecanismo que usa cosmoSIS para pasar datos entre módulos. Para una serie de parámetros, todos los módulos reciben datos del DataBlock y sus salidas se escriben al mismo.
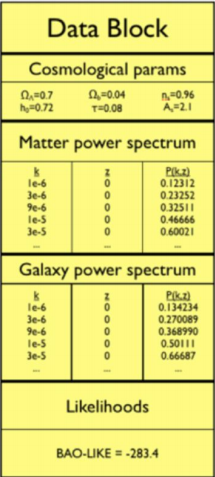

Estructura
Runtime: Capa de código que conecta todos los componentes antes mencionados, coordina la ejecución, y provee un sistema de salida que guarda resultados relevantes y la configuración.
[runtime]
sampler = metropolis
[metropolis]
covmat = covmat.txt
samples = 100000
Rconverge = 0.01
nsteps = 100
Compartir y obtener créditos
CosmoSIS no es un código monolítico, puedes crear diferentes módulos que la gente puede descargar de tu GitHub e incorporarlos en su pipeline
Si tu módulo es muy bueno comparado con lo que ya existe, puedes proponer que se agregue a la librería estándar de cosmoSIS, y cada vez que alguien lo use deberá citar tu artículo, tesis, etc.




Ejemplos
y
demos
Demo 1: Obtener funciones teóricas en cosmología estándar para una cosmología simple
Este demo calcula las distancias cosmológicas estándars, y el espectro de potencias de CMB y el de materia usando los parámetros cosmológicos dados en el archivo values1.ini
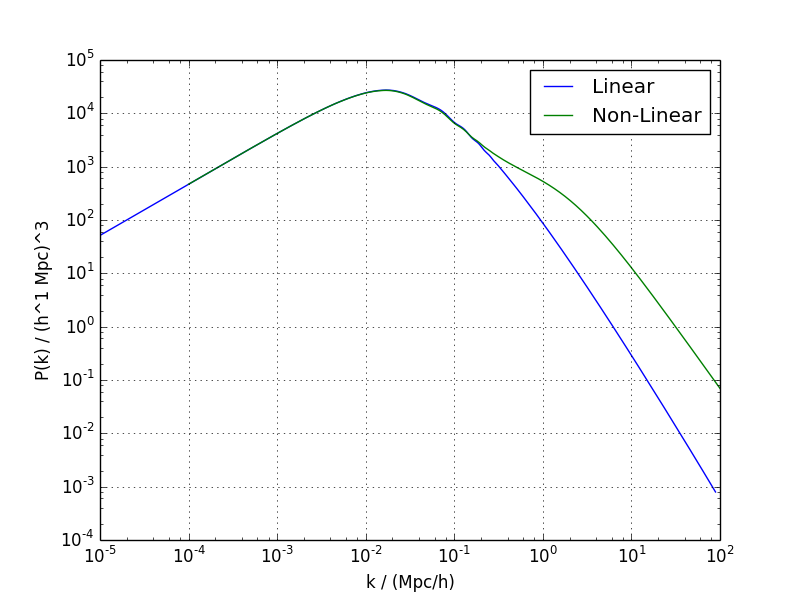

Ejemplos
y
demos
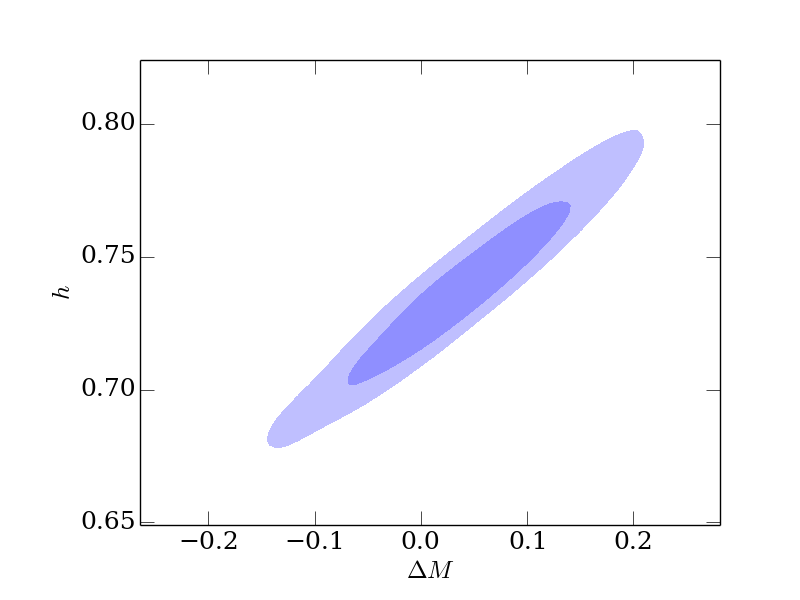
Demo 5: Hacer un análisis de MCMC en datos de supernovas
Este demo hará un análisis completo de MCMC en datos de SDSS-II/SNLS3 Joint Light-curve Analysis (JLA). En http://arxiv.org/abs/1401.4064 hay más información sobre los datos.
¿Preguntas? ¿Dudas?


Favio Vázquez
Cosmólogo y Data Scientist


@faviovaz
