data science

for (physical) scientists 8

dr.federica bianco | fbb.space |    fedhere |    fedhere

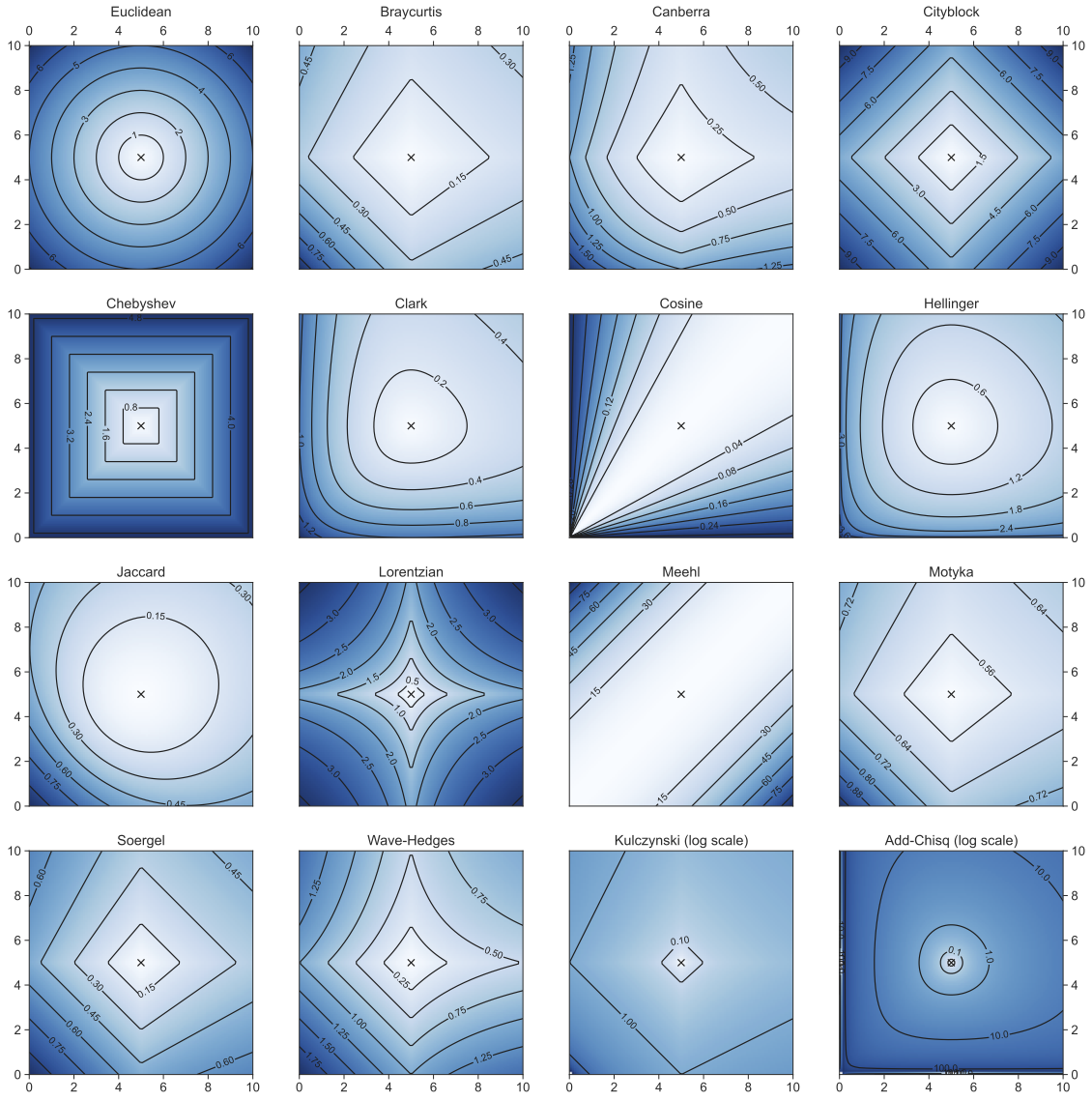
distances

http://bit.ly/dsps_8

this slide deck

k-Nearest Neighbor

Machine Learning

unsupervised learning

identify features and create models that allow to understand structure in the data

unsupervised learning

identify features and create models that allow to understand structure in the data

supervised learning

extract features and create models that allow prediction where the correct answer is known for a subset of the data

k-Nearest Neighbors

Calculate the distance d to all known objects

Select the k closest objects

Assign the most common among the k classes:

# k = 1
d = distance(x, trainingset)
C(x) = C(trainingset[argmin(d)])

C^{kNN}(x) = Y_{(1)}

"lazy learner"

Calculate the distance d to all known objects

Select the k closest objects

Classification:

Assign the most common among the k classes

Regression:
Predict the average (median) of the k target values

k-Nearest Neighbors

Good

non parametric

very good with large training sets

Cover and Hart 1967: As , the -NN error is no more than twice the error of the Bayes Optimal classifier.

k-Nearest Neighbors

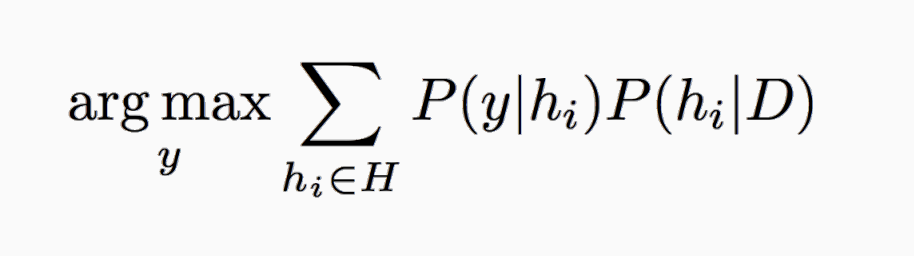
Good

non parametric

very good with large training sets

Cover and Hart 1967: As , the 1-NN error is no more than twice the error of the Bayes Optimal classifier.

Let be the nearest neighbor of .

For , x(t)

Theorem: e[x(t)) = C(xNN)]< e_BayesOpt

e_BayesOpt = argmaxy P(y|x)

Proof: assume

eNN = P(y|x(t)) (1−P(y|xNN)) + P(y|xNN) (1−P(y|x(t))) ≤

(1−P(y|xNN)) + (1−P(y|x(t))) =

2 (1−P(y|x(t)) = 2ϵBayesOpt,

k-Nearest Neighbors

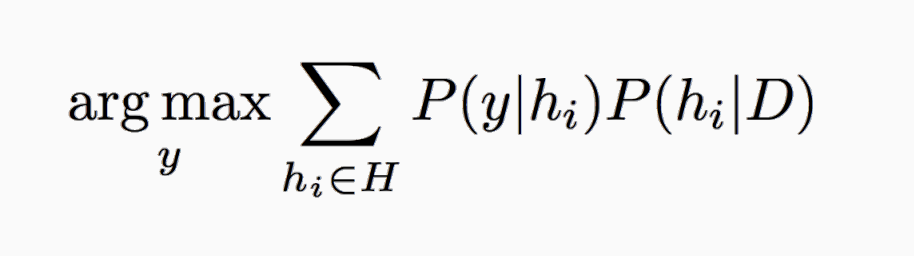
Good

non parametric

very good with large training sets

Not so good

it is only as good as the distance metric

If the similarity in feature space reflect similarity in label then it is perfect!

poor if training sample is sparse

poor with outliers

k-Nearest Neighbors

Wine Example

Lazy Learning

PROS:

Because the model does not need to provide a global optimization the classification is "on-demand".

This is ideal for recommendation systems: think of Netflix and how it provides recommendations based on programs you have watched in the past.

CONS:

Need to store the entire training dataset (cannot model data to reduce dimensionality).

Training==evaluation => there is no possibility to frontload computational costs

Evaluation on demand, no global optimization - doesn’t learn a discriminative function from the training data but “memorizes” the training dataset instead.

distances

distance metrics

D(i,j) > 0\\ D(i,j)~=~D(j,i)\\ D(i,j)~<=~D(i,k)~+~D(k,j)

Any algorithm that fulfills the following conditions

D(i,i) = 0\\

distance metrics

continuous variables

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{|x_{i1}-x_{j1}|^p~+~|x_{i2}-x_{j2}|^p~+~...~+~|x_{iN}-x_{jN}|^p} = L_p

D(i,j) > 0\\ D(i,j)~=~D(j,i)\\ D(i,j)~<=~D(i,k)~+~D(k,j)

distance metrics

continuous variables

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^p}

N features (dimensions)

distance metrics

continuous variables

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^p}

Manhattan: p=1

D_{Man}(i,j)~=~\sum_{k=1}^{N}|x_{ik}-x_{jk}|

features: x, y

distance metrics

continuous variables

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^p}

Manhattan: p=1

D_{Man}(i,j)~=~\sum_{k=1}^{N}|x_{ik}-x_{jk}|

features: x, y

distance metrics

continuous variables

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^p}

Euclidean: p=2

D_{Euc}(i,j)~=~\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^2}

features: x, y

distance metrics

Minkowski family of distances

D(i,j)~=~^{p}\sqrt{\sum_{k=1}^{N}|x_{ik}-x_{jk}|^p}

Great Circle distance

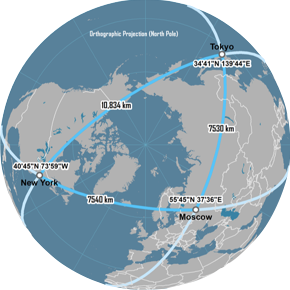
D(i,j)~=~R~\arccos{\left( \sin{\phi}_i \cdot \sin{\phi_j} ~+~ \cos{\phi_i} \cdot \cos{\phi_j} \cdot \cos{\Delta\lambda} \right)}

\phi_i,\lambda_i,\phi_j,\lambda_j

features

latitude and longitude

continuous variables

import scipy as sp

sp.spatial.distance.pdist(X) # the pairwise distance: returns (N**2  - N )/2 values for N objects

sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]])) 
#returns the NXN matrix of distances

plt.imshow(sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]]))) 
#you can visualize the NXN matrix


plt.xlabel("wine")
plt.ylabel("wine");
plt.colorbar(label="distance");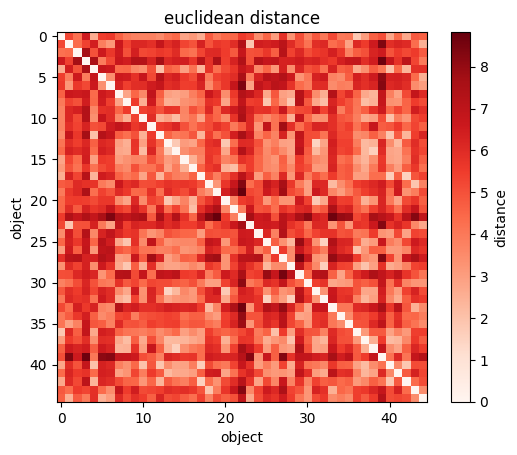

import scipy as sp

sp.spatial.distance.pdist(X) # the pairwise distance: returns (N**2  - N )/2 values for N objects

sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]])) 
#returns the NXN matrix of distances

plt.imshow(sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]]))) 
#you can visualize the NXN matrix


plt.xlabel("wine")
plt.ylabel("wine");
plt.colorbar(label="distance");

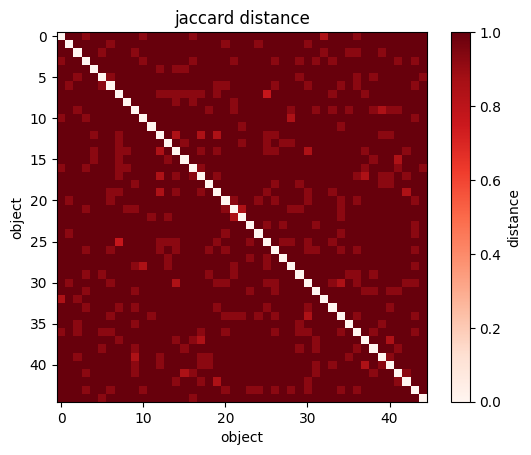
import scipy as sp

sp.spatial.distance.pdist(X) # the pairwise distance: returns (N**2  - N )/2 values for N objects

sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]],
                                                        metric='jaccard')) 
#returns the NXN matrix of distances

plt.imshow(sp.spatial.distance.squareform(sp.spatial.distance.pdist(wines[["Alcohol", "Magnesium"]]))) 
#you can visualize the NXN matrix


plt.xlabel("wine")
plt.ylabel("wine");
plt.colorbar(label="distance");

#Great Circle Distance in the sky
import astropy.units as u
from astropy.coordinates import SkyCoord
#The on-sky separation can be computed with the astropy.coordinates.BaseCoordinateFrame.separation() 
#or astropy.coordinates.SkyCoord.separation() methods, 
#which computes the great-circle distance (not the small-angle approximation):

c1 = SkyCoord('5h23m34.5s', '-69d45m22s', frame='icrs')
c2 = SkyCoord('0h52m44.8s', '-72d49m43s', frame='fk5')
sep = c1.separation(c2)

Angle 20.74611448 deg

from shapely.geometry import Point
import geopandas as gpd
pnt1 = Point(80.99456, 7.86795)
pnt2 = Point(80.97454, 7.872174)
points_df = gpd.GeoDataFrame({'geometry': [pnt1, pnt2]}, crs='EPSG:4326')
points_df = points_df.to_crs('EPSG:5234')
points_df2 = points_df.shift() #We shift the dataframe by 1 to align pnt1 with pnt2
points_df.distance(points_df2)

https://www.codedrome.com/calculating-great-circle-distances-in-python/

https://pypi.org/project/great-circle-calculator/

from math import radians, degrees, sin, cos, asin, acos, sqrt
def great_circle(lon1, lat1, lon2, lat2):
    lon1, lat1, lon2, lat2 = map(radians, [lon1, lat1, lon2, lat2])
    return 6371 * (acos(sin(lat1) * sin(lat2) + cos(lat1) * 
                        cos(lat2) * cos(lon1 - lon2))) #km

distance metrics

Uses presence/absence of features in data

: number of features in neither

M_{i=0,j=0}

: number of features in both

M_{i=1,j=1}

: number of features in i but not j

M_{i=1,j=0}

: number of features in j but not i

M_{i=0,j=1}

categorical variables:

binary

What is the distance between a leopard and a lizard?

- they both have tails

- only lizards have scales

- neither have wings

distance metrics

Uses presence/absence of features in data

: number of features in neither

M_{i=0,j=0}

: number of features in both

M_{i=1,j=1}

: number of features in i but not j

M_{i=1,j=0}

: number of features in j but not i

M_{i=0,j=1}

categorical variables:

binary

What is the distance between a leopard and a lizard?

- they both have tails

- only lizards have scales

- neither have wings

distance metrics

	1	0	sum
1	M11	M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

observation i

}

		0	sum
1		M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

distance metrics

Simple Matching Distance

SMD(i,j)~=~1~- SMC(i,j)

Uses presence/absence of features in data

: number of features in neither

M_{i=0,j=0}

: number of features in both

M_{i=1,j=1}

: number of features in i but not j

M_{i=1,j=0}

: number of features in j but not i

M_{i=0,j=1}

Simple Matching Coefficient

or Rand similarity

SMC(i,j)~=~\frac{M_{i=0,j=0} + M_{i=1,j=1}}{M_{i=0,j=0} + M_{i=1,j=0} + M_{i=0,j=1} + M_{i=1,j=1}} = \frac{2}{3}

	1	0	sum
1	M11	M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

observation i

observation j

}

categorical variables:

binary

		0	sum
1	M11	M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

lizard/leopard

distance metrics

Jaccard similarity

J(i,j)~=~\frac{M_{i=1,j=1}}{M_{i=0,j=1}+M_{i=1,j=0}+M_{i=1,j=1}} = \frac{1}{2}

Jaccard distance

D(i,j)~=~1 - J(i,j)

	1	0	sum
1	M11	M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

observation i

observation j

}

categorical variables:

binary

lizard/leopard

distance metrics

Jaccard similarity

J(i,j)~=~

Jaccard distance

D(i,j)~=~1 - J(i,j)

	1	0	sum
1	M11	M10	M11+M10
0	M01	M00	M01+M00
sum	M11+M01	M10+M00	M11+M00+M01+ M10

observation i

observation j

}

{A\cap B}

{A\cup B}

\frac{A\cap B}{A\cup B}

categorical variables:

binary

distance metrics

Jaccard similarity

https://en.wikipedia.org/wiki/Jaccard_index

Application to Deep Learning for image recognition

Convolutional Neural Nets

J(i,j)~=~

\frac{A\cap B}{A\cup B}

categorical variables:

binary

distance metrics

https://docs.scipy.org/doc/scipy/reference/spatial.distance.html

3 whitening

Data can have covariance (and it almost always does!)

PLUTO Manhattan data (42,000 x 15)

axis 1 -> features

axis 0 -> observations

Data can have covariance (and it almost always does!)

PLUTO Manhattan data (42,000 x 15)

axis 1 -> features

axis 0 -> observations

COVARIANCE = correlation / variance

https://www.tylervigen.com/spurious-correlations

Data can have covariance (and it almost always does!)

https://www.tylervigen.com/spurious-correlations

Data can have covariance (and it almost always does!)

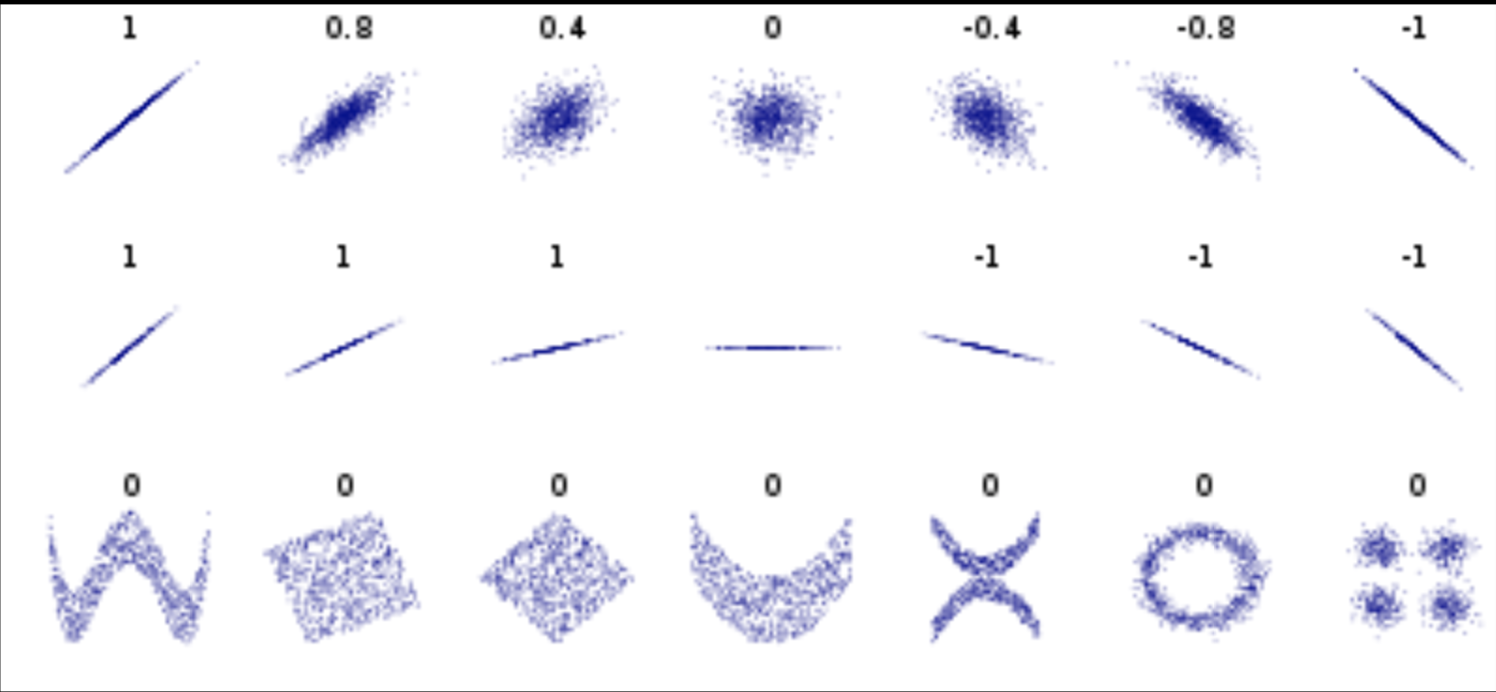
Pearson's correlation (linear correlation)

{\displaystyle r_{xy}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}}}

Generic preprocessing... WHY??

Worldbank Happyness Dataset https://github.com/fedhere/MLPNS_FBianco/blob/main/clustering/happiness_solution.ipynb

Clustering without scaling:

only the variable with more spread matters

Skewed data distribution:

std(x) ~ range(y)

Generic preprocessing... WHY??

Worldbank Happyness Dataset https://github.com/fedhere/MLPNS_FBianco/blob/main/clustering/happiness_solution.ipynb

Clustering without scaling:

only the variable with more spread matters

Skewed data distribution:

std(x) ~ range(y)

Clustering

Classifying &

regression

Unsupervised learning

understanding structure
anomaly detection
dimensionality reduction

Supervised learning

classification
prediction
feature selection

unsupervised vs supervised learning

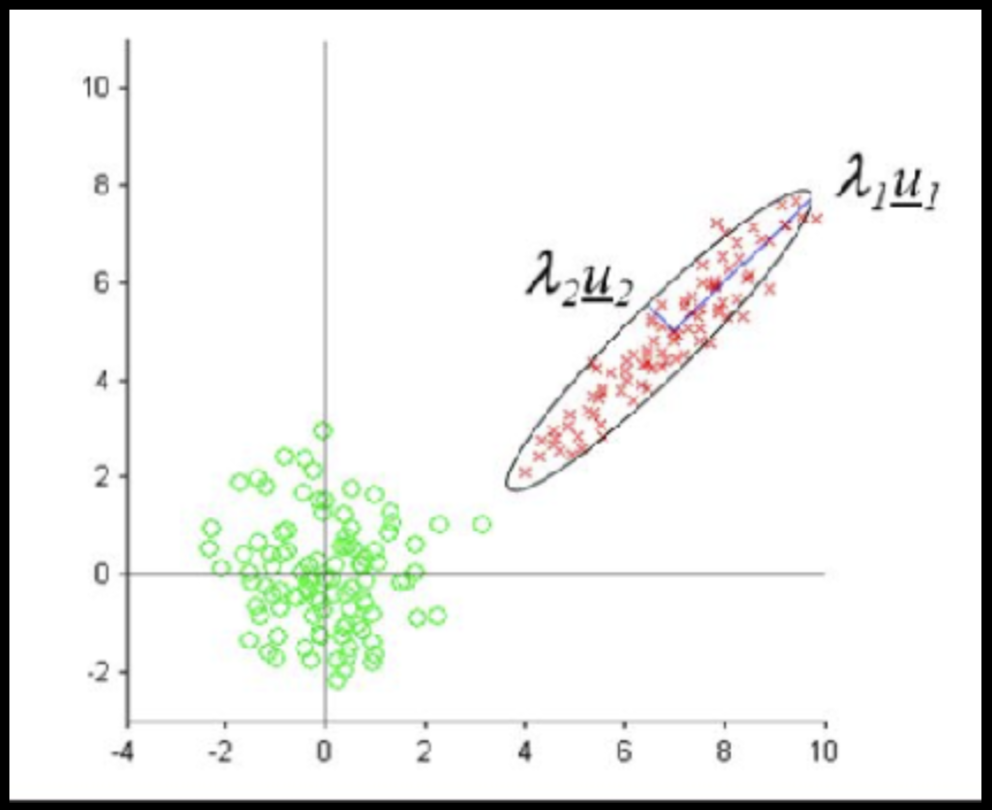
Data that is not correlated appear as a sphere in the Ndimensional feature space

Data can have covariance (and it almost always does!)

ORIGINAL DATA

STANDARDIZED DATA

Generic preprocessing

Generic preprocessing... WHY??

Worldbank Happyness Dataset

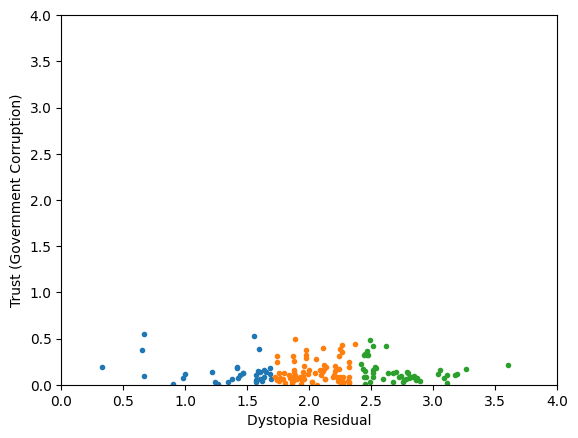
Classification/Clustering without scaling:

only the variable with more spread matters

Generic preprocessing... WHY??

Worldbank Happyness Dataset

Classification/Clustering without scaling:

only the variable with more spread matters

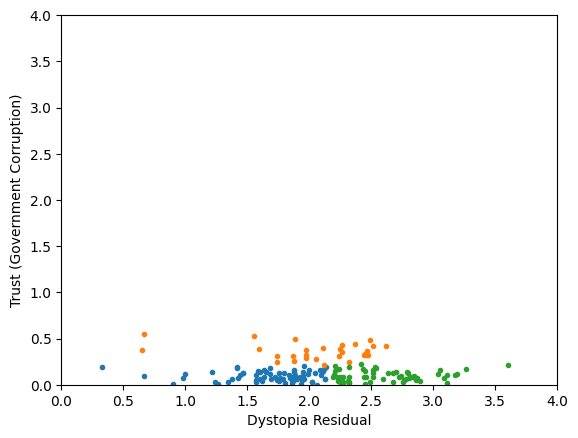
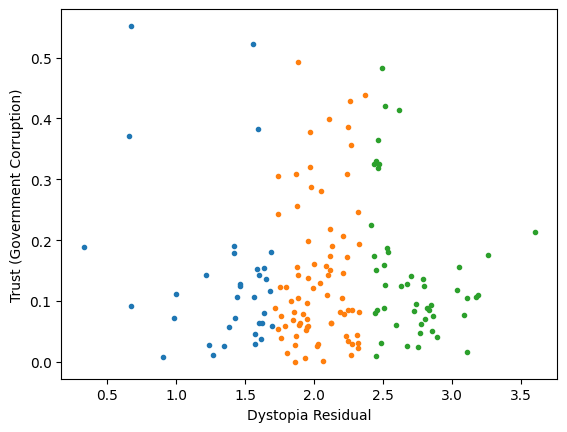
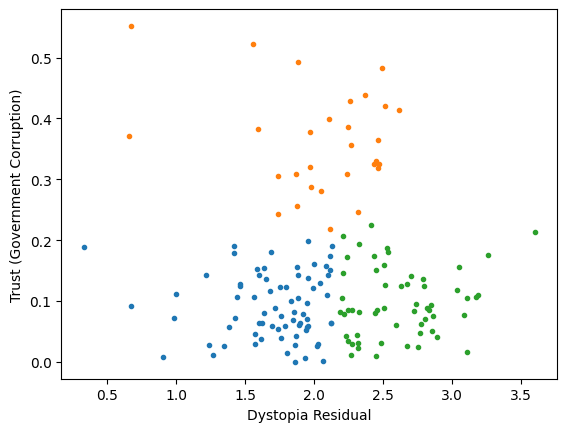
Classification/Clustering

after scaling:

both variables matter equally

Data that is not correlated appear as a sphere in the Ndimensional feature space

Data can have covariance (and it almost always does!)

ORIGINAL DATA

STANDARDIZED DATA

Generic preprocessing

for each feature: divide by standard deviation and subtract mean

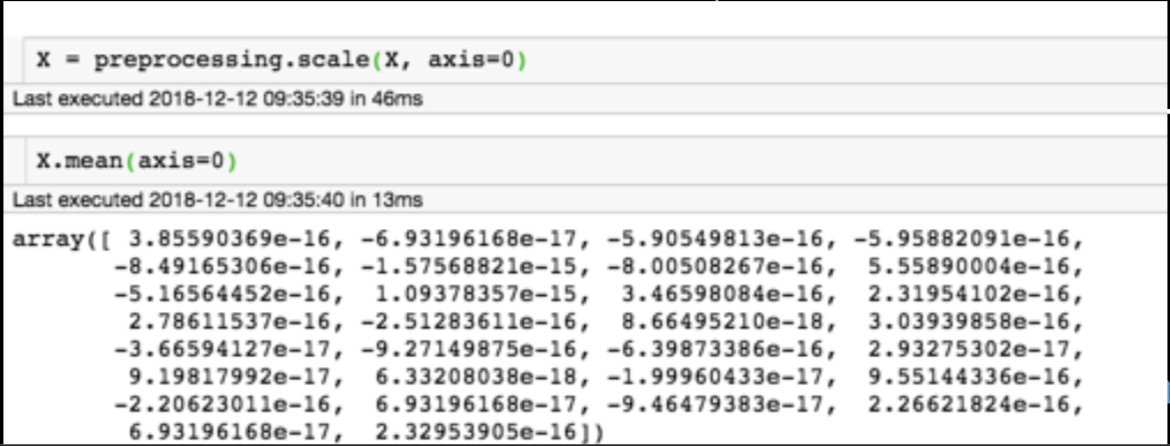
Generic preprocessing: most commonly, we will just correct for the spread and centroid

whitening

The term "whitening" refers to white noise, i.e. noise with the same power at all frequencies"

PLUTO Manhattan data (42,000 x 15) correlation matrix

axis 1 -> features

axis 0 -> observations

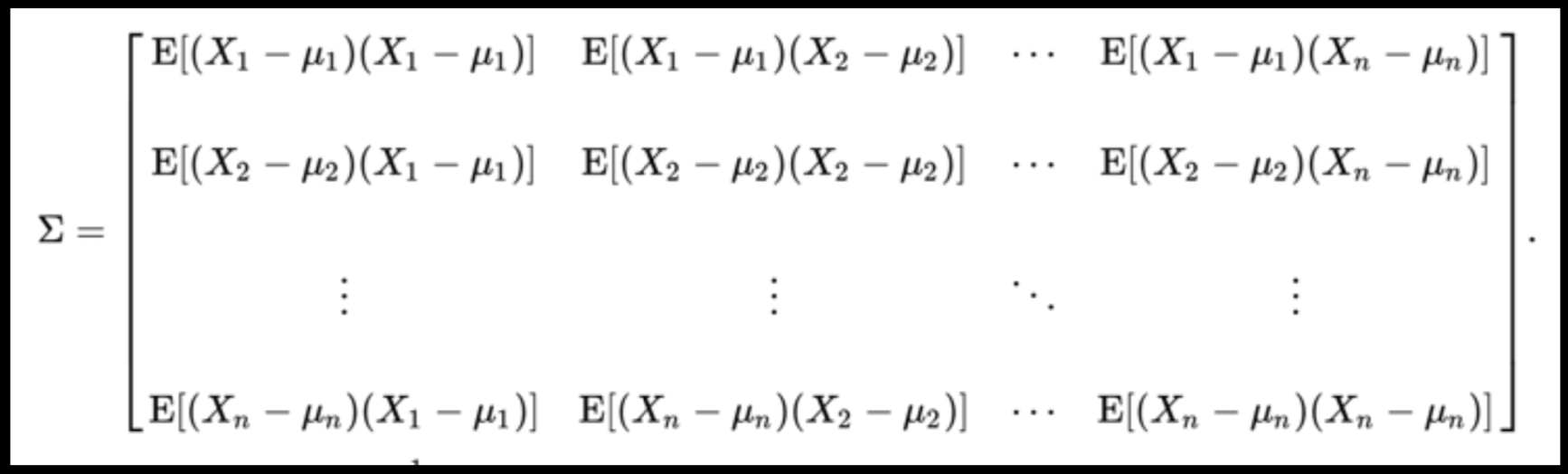
Data can have covariance (and it almost always does!)

PLUTO Manhattan data (42,000 x 15) correlation matrix

A covariance matrix is diagonal if the data has no correlation

Data can have covariance (and it almost always does!)

Full On Whitening

find the matrix W that diagonalized Σ

from zca import ZCA
import numpy as np

X = np.random.random((10000, 15)) # data array

trf = ZCA().fit(X)

X_whitened = trf.transform(X)

X_reconstructed =

trf.inverse_transform(X_whitened)

assert(np.allclose(X, X_reconstructed))

: remove covariance by diagonalizing the transforming the data with a matrix that diagonalizes the covariance matrix

this is at best hard, in some cases impossible even numerically on large datasets

Generic preprocessing: other common schemes

for image processing (e.g. segmentation) often you need to mimmax preprocess

from sklearn import preprocessing

Xopscaled = preprocessing.minmax_scale(image_pixels.astype(float), axis=1) 
Xopscaled.reshape(op.shape)[200, 700]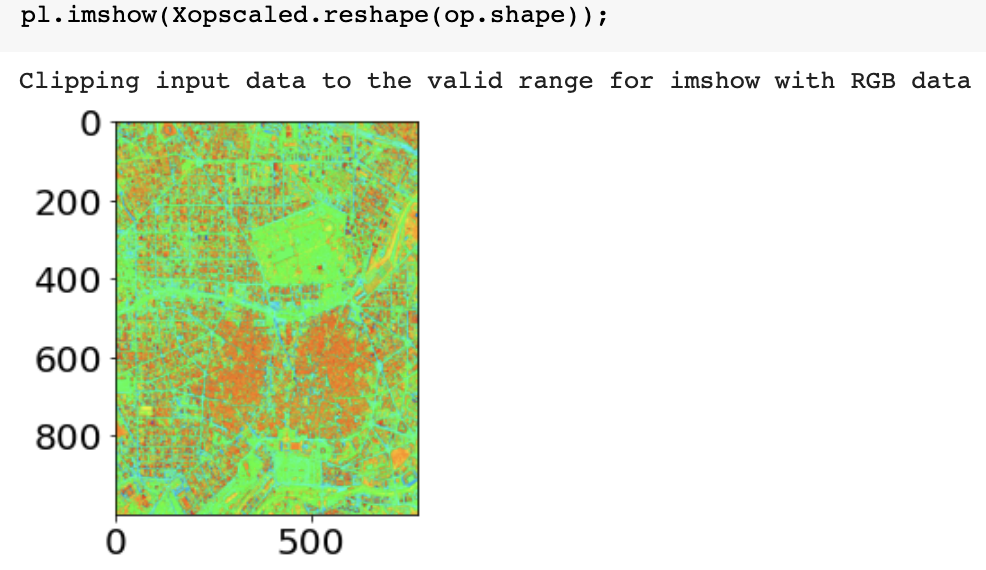

before

after (looks the same but colorbar different)

-107

273