ML for physical and natural scientists 2023 5


dr.federica bianco | fbb.space |    fedhere |    fedhere

K-NN - CART

this slide deck:

https://slides.com/federicabianco/mlpns23_5

Extraction of features

1

 

midterm

https://github.com/fedhere/MLPNS2021/blob/main/midterm/MLPNS2021midterm.ipynb

Consider a classification task:

if I want to use machine learning methods I need to choose:

use raw representation:

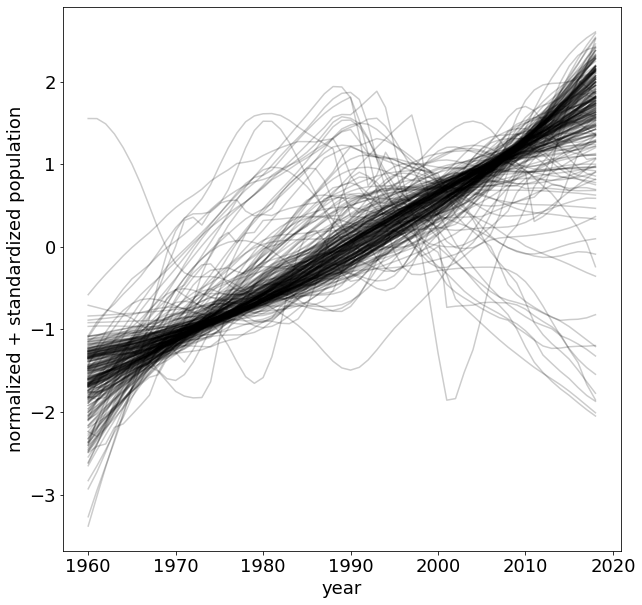
e.g. clustering:

1) take each time series and standardize it

(mean 0 standard 1). 

2) for each time stamps compare them to the expected value (mean and stdev)

essentially each datapoint is treated as a feature

Consider a classification task:

if I want to use machine learning methods (e.g. clustering) I need to choose:

use raw representation

1) take each time series and standardize it (μ=0 ; σ=1). 

2) for each time stamps compare them to the expected value (μ & σ)

 

problems:

  1. scalability: for N time series of lenght d the dataset has dimension Nd
  2. time series may be asynchronous
  3. time series may be warped

(in small dataset you can optimize over warping and shifting but in large dataset this solution is computationally limited)

essentially each datapoint is treated as a feature

Consider a classification task:

if I want to use machine learning methods (e.g. clustering) I need to choose:

choose a low dimensional representation

essentially each datapoint is treated as a feature

Extract features that describe the time series:

simple descriptive statistics (look at the distribution of points, regardless of the time evolution: 

  • mean
  • standard deviation
  • other moments (skewness, kurtosis)

parametric features (based on fitting model to data):

  • slope of a line fit
  • intercept of a line fit
  • linear regression R2

Consider a classification task:

the learned representations should:

  • preserve the pairwise similarities and serve as feature vectors for machine learning methods;
  • lower bound the comparison function to accelerate similarity search;
  • allow using prefixes of the representations (by ranking their coordinates in descending order of importance) for scaling methods under limited resources;
  • support efficient and memory-tractable computation for new data to enable operations in online settings; and
  • support efficient and memory-tractable eigendecomposition of the datato-data similarity matrix to exploit highly effective methods that rely on such cornerstone operation.

http://www.vldb.org/pvldb/vol12/p1762-paparrizos.pdf

Supervise learning

2

what is machine learning?

classification

prediction

feature selection

supervised learning

understanding structure

organizing/compressing data

anomaly detection dimensionality reduction

unsupervised learning

classification

supervised learning methods

(nearly all other methods you heard of)

learns by example

  • Need labels, in some cases a lot of labels
  • Dependent on the definition of similarity

  • Similarity can be used in conjunction to parametric or non-parametric methods

used to:

classify, predict (regression)

supervised learning methods

(nearly all other methods you heard of)

learns by example

  • Need labels, in some cases a lot of labels
  • Dependent on the definition of similarity

  • Similarity can be used in conjunction to parametric or non-parametric methods

used to:

classify, predict (regression)

clustering vs classifying

x

y

unsupervised

supervised

observed features:

(x, y)

models typically return a partition of the space

target features:

(color)

goal is to partition the space so that the unobserved variables are

 

separated in groups

consistently with

an observed subset

x

y

observed features:

(x, y)

if x**2 + y**2 <= (x-a)**2 + (y-b)**2 :
	return blue
else:
	return orange

target features:

(color)

A subset of variables has class labels. Guess the label for the other variables

supervised ML: classification

SVM

finds a hyperplane that optimally separates observations

x

y

observed features:

(x, y)

Tree Methods

split spaces along each axis separately

A subset of variables has class labels. Guess the label for the other variables

split along x

if x <= a :
	if y <= b:
      		return blue
return orange

then

along y

target features:

(color)

supervised ML: classification

x

y

observed features:

(x, y)

KNearest Neighbors

Assigns the class of closest neighbors

A subset of variables has class labels. Guess the label for the other variables

split along x

k = 4
if (label[argsort(distance((x,y), trainingset))][:k] == "blue").sum() > (labels[argsort(distance((x,y), trainingset))][:k] == "orange").sum():
	return blue
return orange

target features:

(color)

supervised ML: classification

k-Nearest    Neighbor

3

 

k-Nearest Neighbors 

Calculate the distance d to all known objects

Select the k closest objects

Assign the most common among the k classes: 
# k = 1
d = distance(x, trainingset)
C(x) = C(trainingset[argmin(d)])
C^{kNN}(x) = Y_{(1)}
C^{kNN}(x) = Y_{(1)}

"lazy learner"

Calculate the distance d to all known objects

Select the k closest objects


Classification: 
Assign the most common among the k classes

 

Regression:
Predict the average (median) of the k target values

 

k-Nearest Neighbors

Good

non parametric

very good with large training sets

Cover and Hart 1967: As n→∞, the 1-NN error is no more than twice the error of the Bayes Optimal classifier. 

 

k-Nearest Neighbors

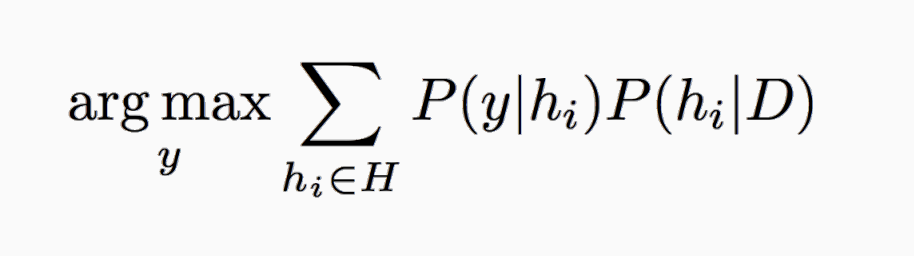
Good

non parametric

very good with large training sets

Cover and Hart 1967: As n→∞, the 1-NN error is no more than twice the error of the Bayes Optimal classifier. 

Let xNN be the nearest neighbor of x.

For n→∞,  xNN→x(t) => dist(xNN,x(t))→0

Theorem: e[C(x(t)) = C(xNN)]< e_BayesOpt

e_BayesOpt = argmaxy P(y|x)

Proof: assume P(y|xt) = P(y|xNN)

(always assumed in ML)

eNN = P(y|x(t)) (1−P(y|xNN)) +          P(y|xNN) (1−P(y|x(t))) ≤

(1−P(y|xNN)) + (1−P(y|x(t))) =

2 (1−P(y|x(t)) = 2ϵBayesOpt,

 

 

k-Nearest Neighbors

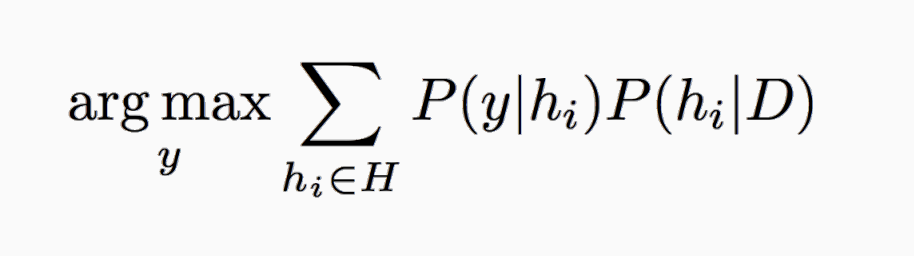
Good

non parametric

very good with large training sets

 

Not so good

it is only as good as the distance metric

If the similarity in feature space reflect similarity in label then it is perfect!

 

poor if training sample is sparse

 

poor with outliers

 

 

k-Nearest Neighbors

 

k-Nearest Neighbors

using Kaggle data programmatically https://www.kaggle.com/docs/api

 

Lazy Learning

PROS:

Because the model does not need to provide a global optimization the classification is "on-demand".

 

This is ideal for recommendation systems: think of Netflix and how it provides recommendations based on programs you have watched in the past.

CONS:

Need to store the entire training dataset (cannot model data to reduce dimensionality).

Training==evaluation => there is no possibility to frontload computational costs

Evaluation on demand, no global optimization - doesn’t learn a discriminative function from the training data but “memorizes” the training dataset instead.