¿Qué es?

Cuando luz linealmente polarizada atravieza un material transparente (e.g. vidrio) que se encuentra inmerso en un campo magnético con líneas de fuerza paralelas a la dirección de la luz, el vector de polarización rota un ángulo 

A diferencia de la actividad óptica, el ángulo de giro depende de la dirección del campo.

Modelo de Lorentz

• Los electrones se comportan como osciladores armónicos.
• El movimiento isotrópico es equivalente a un movimiento longitudinal paralelo a la luz, y dos movimientos circulares en sentidos opuestos perpendiculares a la luz.

Efecto Zeeman

• Ocasiona que las líneas de absorción se dividan en presencia de un campo magnético.
• Las frecuencias de absorción equivalen a las frecuencias resonantes en el modelo de Lorentz.
• Los índices de dispersión circulares alrededor de estas frecuencias son anómalos.

• La luz linealmente polarizada se puede representar con dos componentes circulares en sentidos opuestos.
• Hay una diferencia de velocidades entre las dos componentes circulares.
• Estos resulta en un giro del eje de polarización lineal.

Arreglo experimental

¿Cómo medimos el campo?

Resultados

Constante de Verdet

Haciendo el ajuste a una recta de la forma:

obtenemos la constante de Verdet

Resultados

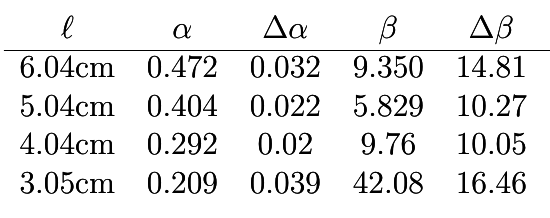
Cristal F-2

Cristal SF-5

Valores calculados

¿Depende de la longitud de onda?

Se sabe que la teoría depende explícitamente de la longitud de onda, por eso se usó luz coherente monocromática en lugar de una fuente de luz blanca. Para ver el efecto de la longitud de onda sobre la rotación del plano de polarización se cambió el láser verde por un láser rojo.

Resultados

Constante de Verdet

Aplicando el ajuste

se puede obtener la constante de Verdet