BIT (not Bit)

Or Fenwick Tree. Whatever.

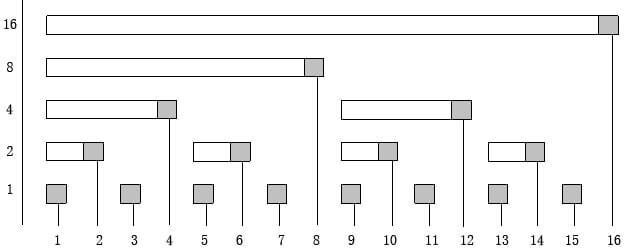
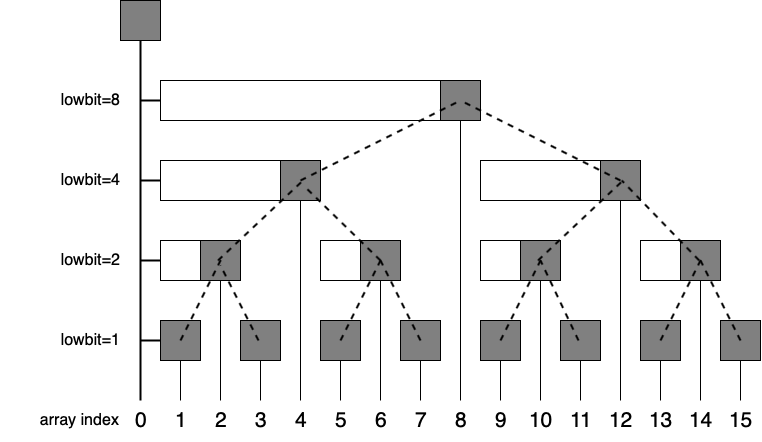
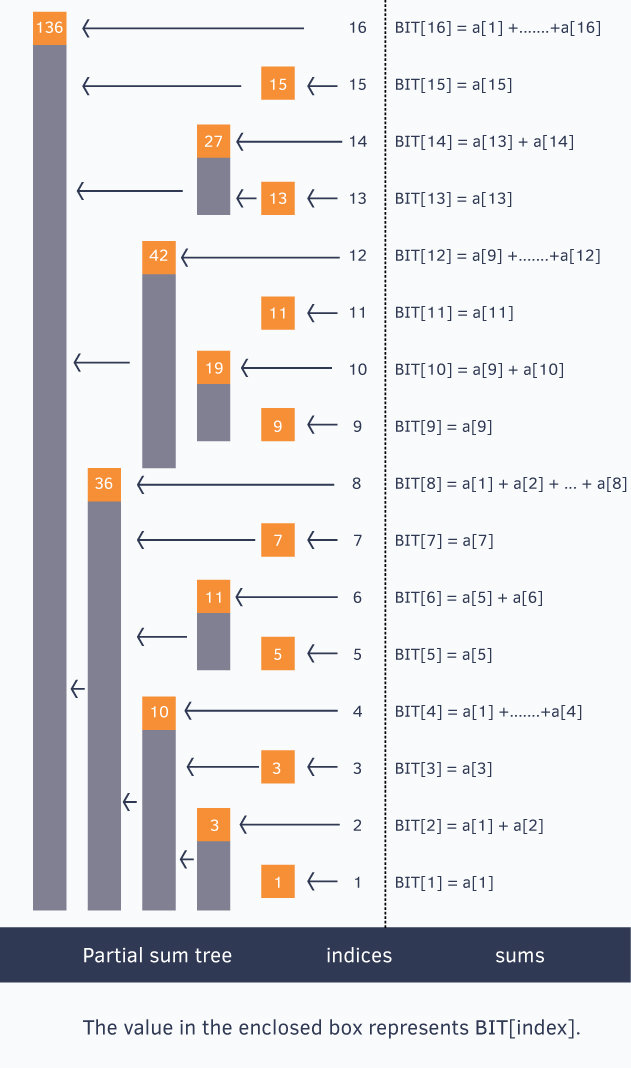
到底可以幹嘛？

\(O(\log(n))\) 維護前綴()！

其實後綴也可以

必須要符合結合律的操作才可以喔！

Sum
minMax
XOR?

扣的超短

struct BIT{
    int n, val[N];
    inline void init(int _n){
        n = _n;
        for(int i = 0; i <= n; ++i)
            val[i] = 0;
    }
    inline void modify(int p, int v){
        for(; p <= n; p += p & -p) val[p] += v;
    }
    inline int query(int p){
        int ans = 0;
        for(; p > 0; p -= p & -p) ans += val[p];
        return ans;
    }
} bit;

單點修改、區間查詢

區間修改、單點查詢？

差分！

該知道的都差不多了

\(O(n)\) 初始化

struct BIT{
    int n, val[N];
    inline void init(int _n, int v[]){
        n = _n;
        for(int i = 1; i <= n; ++i)
            val[i] = 0;
        for(int i = 1; i <= n; ++i){
            val[i] += v[i];
            if(i + (i & -i) <= n)
                val[i + (i & -i)] += val[i];
        }
    }
} bit;

Sauce

\(O(\log(n))\) 搜

struct BIT{
    int n, val[N];
    inline int search(int v){
        int sum = 0, p = 0;
        for(int i = 31 - __builtin_clz(n); i > 0; --i)
            if(p + (1 << i) <= n and sum + val[p + (1 << i)] < v)
                p += 1 << i, sum += val[p];
        return p + 1;
    }
} bit;

Sauce

題單

通常難的都不是 BIT 本身QWQ

TIOJ 1080

給一長度為 \(n, n \leq 10^5\)的 32-bit 整數序列 \(S\)，

求有多少對 \(i, j\) 使得 \(i < j, S_i > S_j\)

Hint:

離散化＋值域 BIT

TIOJ 2026

維護一個 multiset

支援兩種操作：

  1. ​插入一個數字 \(x, 1 \leq x \leq 10^6\)
  2. 查詢集合中第 \(\lceil\frac{|S|}{2}\rceil\) 大的數（保證 \(|S|\) 是奇數）

Hint:

值域 BIT ＋二分搜（或\(O(\log(n)\)搜）

TIOJ 1305

維護一個 32-bit 整數集合 \( S \)，

支援三種操作：

  1. 插入一整數 \(x\)
  2. 移除一整數 \(x\)
  3. 查詢第 \(k\) 小整數

Hint:

先全部離散化

TIOJ 1869

維護一個 \(n \cdot n, n \leq 1024\) 的棋盤，

支援兩種操作：

  1. 在某一格放上或拿走 \(z\) 個石頭
  2. 查詢一個矩形範圍有多少石頭

\(z\) 在 C++ short 範圍內。

Hint:

二為前綴和＋二維BIT

TIOJ 1710

給定一個長度為 \(n ( n \leq 50000) \) 的

序列 \(a ( \forall i, 1 \leq a_i \leq 10^5 ) \)，

求有多少組 \((i, j, k)\)，

\(s.t.\ i < j < k, a_i < a_j < a_k \cup a_i > a_j > a_k\)

Hint:

枚舉 \(j\)，做兩次

TIOJ 1272

給一棵有 \(n\ (n \leq 10^5) \)個節點的有根樹，

每個節點紀錄一個布林值，

支援兩種操作：

  1. 將一個節點的值以及其子樹的值翻轉
  2. 查詢一個節點的值

Hint:

樹壓平，區間修改，XOR

TIOJ 2066

給一長度為 \( n \) 整數序列，

求有多少長度為 \(x (1 \leq x \leq k) \) 的

嚴格遞增子序列（ LIS ）

\( n \leq 10^5, k \leq 70 \)

Hint:

對 \(k\)，值域做事

TIOJ 1345

給一個一維或二維或三維的細格，

並在其中一些格子放玩具，

求有多少對玩具點對，

使得其曼哈頓距離 \(\leq D\)

Hint:

展開式子，曼哈頓轉切比雪夫

Made with Slides.com