網路流淺淺談
聽說不難?
簡介
講師:FHVirus
因為想學 Flow 所以當講師
課程內容
- 網路流問題定義
- Max flow/Min cut 定理
- 建模
- Ford-Fulkerson、Edmonds-Karp、
Dinic 實作與複雜度 - 一堆題目
Disclaimer
- 網路流相關的主題還有MCMF、最小割相關、線性規劃等等演算法今天都不會教(講師不會),請不要覺得這就是 Flow 的大部分。
- 今天的證明不會太嚴謹(講師不會),有興趣自己查資料
- IOI 不會考 Flow,但是能競、選訓營不保證不考。
面對網路流的心態
可能僅限今天
面對網路流題目時:
- 做好通靈的準備
很多題模最難的是看猜到他要用 Flow - 把網路流演算法當作黑盒子
在想要怎麼流(建模)的時候不要去在意演算法是怎麼運作的,想清楚確定複雜度是好的之後砸下去就對了 - 不要中毒
就算是 Flow 的題目也不一定需要 Flow 演算法,好好觀察思考,確定得用 Flow 再砸
網路流問題
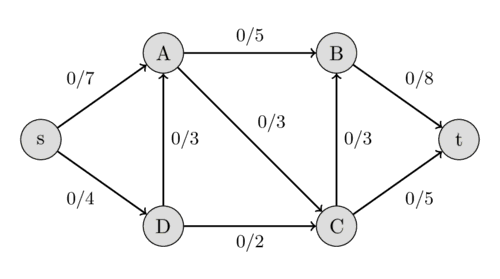
在一張有向圖 \(G = (V, E) \)上,
每個邊有一個非負實數的權重 \(c(u, v) \ge 0\) 代表容量,
(若 \((u, v) \notin E\),則 \(c(u, v) = 0\))
並有兩個特殊點: 源點 \(s\) 與匯點 \(t\)。
一個可行流是一個函數 \(f : V \times V \mapsto \mathbb{R}\),
其滿足以下條件:
- \(f(u, v) \le c(u, v), \forall (u, v) \in V \times V\) (流量限制)
- \(f(u, v) = -f(v, u), \forall (u, v) \in V \times V\)(流量對稱)
- \(\sum_{v \in V}{f(u, v)} = 0, \forall u \in V \backslash \{s, t\}\)(流量守恆)
定義這個網路流的流量為 \(\sum_{v \in V}{f(s, v)}\),
而最大的可行流則稱為最大流。
所以網路流黑盒子做的事情就是:
給定一張有向帶權圖 \(G = (V, E)\) 以及 \(s, t\),
吐出他的最大流。
這邊就當作你有黑盒子了。
沒有也沒關係,反正黑盒子就是黑盒子。
黑盒子使用範例
void solve(){
int n, m; cin >> n >> m;
// 設 n 個點, 1 為源點, n 為匯點
din.init(n, 1, n);
for(int u, v, c; m; --m){
cin >> u >> v >> c;
// 增加一條 u 到 v 容量為 c 的邊
din.add(u, v, c);
}
// 我叫你流
cout << din.flow() << '\n';
}
後面才會講黑盒子的實作與複雜度
一些名詞
剩餘網路
1
1
1
2
2
6/7
4/4
2/3
3/3
2/3
4/5
6/8
5/5
1/3
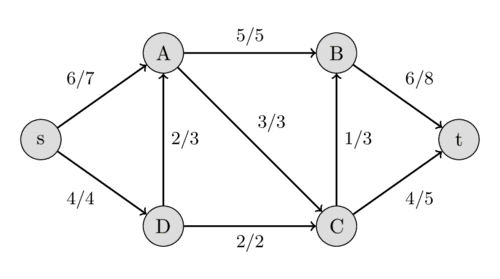
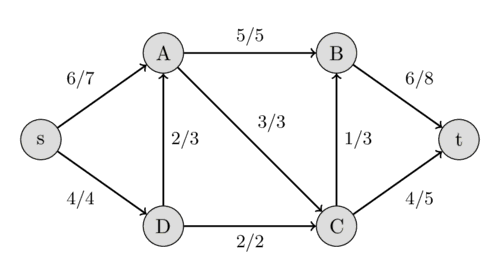
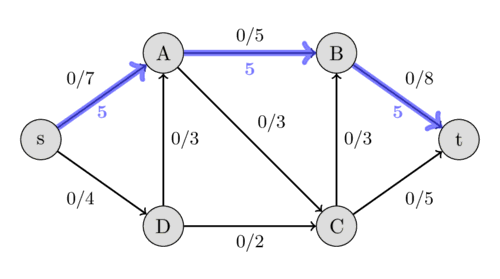
剩餘網路 \(G_r\):現在這個網路還可以怎麼流
注意反向邊(紅色)
擴增路徑
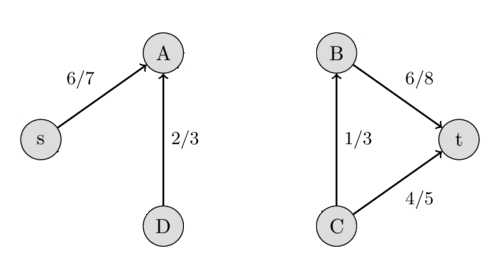
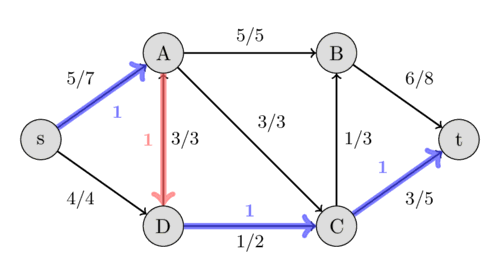
擴增路徑:一條在 \(G_r\) 上從 \(s\) 到 \(t\) 的簡單路徑
也就是剩餘流量 \(> 0\) 的一條簡單路徑
注意反向邊(紅色)
對偶問題與最小割
對偶問題:一體兩面
- 自強樓什麼時候會倒 \(\leftrightarrow\) 自強樓能夠撐到什麼時候
- 最少不遞增子序列數量 \(\leftrightarrow\) 最長遞增子序列長度
- 燒雞 \(\leftrightarrow\) 裝弱(我想不到了)
- 線性規劃有更多好玩的例子
但我不會數學
那麼最大流的對偶問題
是什麼?
\(s\)
\(1\)
\(2\)
\(t\)
7/14
7/7
7/49
看看這個例子
\(s\)
\(1\)
\(2\)
\(t\)
7/14
7/7
7/49
是誰卡住了?
瓶頸?割?🈹️
割
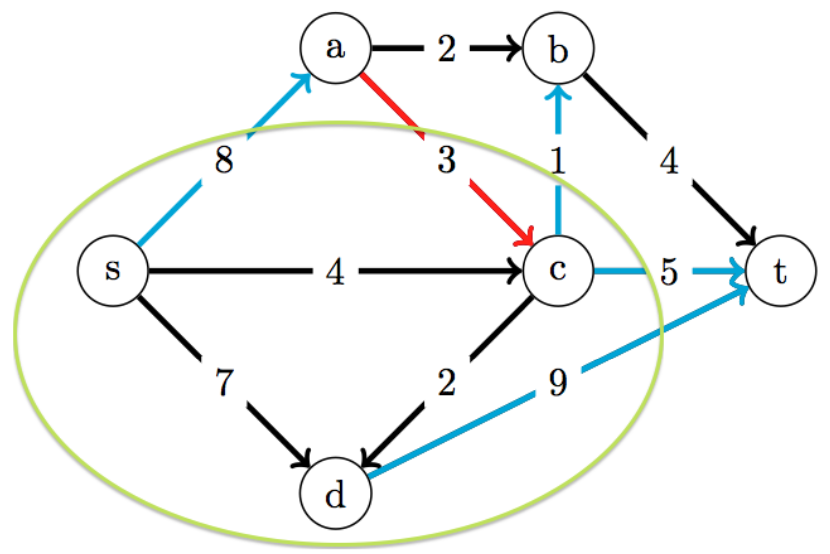
\(Cut(s, t) = \sum_{u \in s}{\sum_{v \in t}{ c(u, v)}}\)
最小割
s 到 t 最窄的那些瓶頸
長得好像最大流的限制?
最小割==最大流?
來不嚴謹的證明吧!
講師不會數學,所以就先證個大概
反正也沒有人想聽
最小割==最大流?
觀察一:
最大流 \(\le\) 最小割
\(\sum_{u \in S}{\sum_{v \in T}{f(u, v)}} \le \sum_{u \in S}\sum_{v \in T}{c(u, v)}\)
應該蠻好理解的?
送出去的流量 \(\le\) 出邊的流量上限
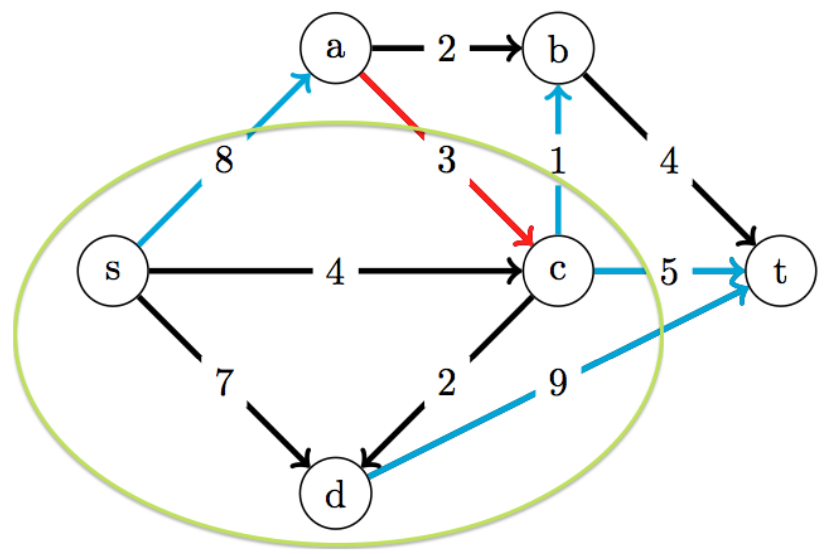
最小割==最大流?
觀察二:
\(f\) 是最大流 \(\Leftrightarrow\) \(G_r\) 沒有擴增路徑
應該顯然吧
最小割==最大流?
Claim:如果 \(f\) 沒有擴增路徑(塞滿了),
則可以找到(構造)一個割 \(C\),
使得 \(\vert C \vert = \vert f \vert\)
最小割==最大流?
構造法:
令所有 \(s\) 在 \(G_r\) 上可以走得到的點在 \(S\),
其餘在 \(T\)。則:
- \(\forall u \in S, v \in T, f(u, v) = c(u, v)\)
- \(\forall u \in S, v \in T, f(v, u) = 0\)
用反證法可知若不滿足這兩點,
則有擴增路徑(\(\rightarrow\leftarrow\))。
最小割==最大流?
構造法:
令所有 \(s\) 在 \(G_r\) 上可以走得到的點在 \(S\),
其餘在 \(T\)。
不但找到了 \(f\) 使得 \(\vert f \vert = \vert C \vert\),
也得知了 \(C\) 每一條邊都被塞滿滿!
最小割=最大流!
盱衡上述:
令最大流 \(f\),構造出的割 \(C\)
- \(\vert f \vert \le\) 所有的可能割
- \(f\) 可以找到一割使得\(\vert f \vert = \vert C \vert\)
\(\Rightarrow\) 最小割=最大流,且 \(C\) 為最小割!
最小割例題
現在 INFOR 社辦某一台電腦被 FHVirus 感染了,
社員們要想辦法在 FHVirus 感染到
存放了重要Jizz資料的某一台電腦前阻止他。
FHVirus 只能透過 \(n\) 台電腦的 \(m\) 條網路線散播,
每一條網路線都有一個貴重程度 \(w_i\),
而社員們只能用剪斷網路線來防禦。
由於 FHVirus 散播速度跟FWT一樣快,
時間所剩不多,請求出
「剪斷線路貴重程度和」最小的防禦方式吧!
註:只要守住「存放了重要Jizz資料的某一台電腦」就好
看出是最小割了嗎?
砸 Flow!
有許多 Flow 題目是要構造出
使用最小割的機會,
請多利用 MFMC 喔。
一些題目
講師要去吃飯
想想看點容量怎麼做?
投票:要不要看雜耍
順便講解例題[0]
建模與更多例題
建模
透過改變/構造圖,
使得既有的演算法能在新圖上得到答案。
題目要最短路
\(\Rightarrow\) 如果能 Dijkstra 就好了⋯⋯
\(\Rightarrow\) 建模維護額外資訊!
把每一個點 \(u\) 變成 \(u_0 \sim u_{1023}\),
代表到 \(u_i\) 且 \(xor\) 值為 \(i\) 的最短路。
Flow 也可以建模!
題目要點容量
\(\Rightarrow\) 如果能換成邊容量就好了⋯⋯
\(\Rightarrow\) 建模,把點變成邊!
對於每一個點 \(u\),拆成 \(u_{in}, u_{out}\),
並建兩點間容量為點容量大小的邊!
最大二分圖匹配數?
每一個紅點要對應到一個藍點,
求最多紅藍出CP點對數
\(\Rightarrow\) 如果能換成最大流量就好了⋯⋯
\(\Rightarrow\) 建模,把匹配變成流量為 \(1\) 的邊!
對於每一個紅點 \(u\),建 \((s, u, 1)\) 的邊;
對於每一個藍點 \(v\),建 \((v, t, 1)\) 的邊;
對原圖上的 \((u, v)\),建 \((u, v, 1)\) 的邊。
這樣最大流就是最大匹配數!
最大二分圖匹配數?
先爆個雷
匹配用 Dinic 的複雜度是 \(O(E \sqrt{V})\),
超級快!跟 ZCK 破台的速度一樣
(用擴增路徑找匹配是 \(O(VE)\))
要選不選又沒辦法好好 DP
看到這種東西:
- 拿 \(u\) 會賺 \(c\) 。
- 拿 \(u\) 要花 \(c\) 。
- 拿 \(u\) 不拿 \(v\) 要花 \(c\)。
- 拿 \(u\) 一定要拿 \(v\) 。
也就是拿 \(u\) 不拿 \(v\) 要花 \(INF\)。
又沒有辦法好好 DP 的時候⋯⋯
要選不選又沒辦法好好 DP
每一個東西分成要選或不選兩類⋯⋯
\(\Rightarrow\) 如果能用最小割就好了⋯⋯
\(\Rightarrow\) 建模,把要不要選變成分在 \(S\) 或 \(T\)!
把上面四種關係(實際上是三種)
巧妙地變成邊之後,
最小花費就變成最小割!
怎麼做?
假設要選的在 S-cut,不選的在 T-cut:
- 拿 \(u\) 要花 \(c\)
\(cap(u, t) = c\)
- 拿 \(u\) 不拿 \(v\) 要花 \(c\):
\(cap(u, v) = c\)
- 拿 \(u\) 會賺 \(c\) :?
容量不能是負的!
怎麼做?
拿 \(u\) 會賺 \(c\) :
先假裝賺了 \(c\) ,等等決定不選再扣回去!
\(ans = ans + c, cap(s, u) = c\)
小結
遇到分兩類又不能 DP
\(\rightarrow\) 試試看最小割!
還有一大堆酷酷的模沒有講到,
有興趣可以去看 IOIC 講義。
(沒有的話就祈禱明年也能順利辦成吧!)
這樣應該會做例題[2]了吧!
什麼?你說你沒有黑盒子?
你又沒有要裝黑幹嘛要黑盒子
終於要開箱黑盒子了
Ford-Fulkerson
隨便做隨便唬爛
每次找一條增廣路徑,沿著他增廣。
假設流量為 \(f\),沿途所有邊 \(c = c - f\),
沿途所有邊的反向邊 \(c = c + f\)。
反向邊的概念很重要。
隨便做隨便唬爛
int fordFulkerson(){
int ans = 0, tmp;
while(true){
// 反正就一直增廣到不行
tmp = findAugPath(s, INF);
if(tmp == 0) break;
ans += tmp;
}
return ans;
}不實用所以就不實作了。
複雜度?
- 流量上限有無理數的話,演算法不一定會結束!
- 流量限制是整數的話,複雜度是 \(O(E \vert f \vert)\)
根據 Integral Flow Theorem,流量限制是整數的話,
每次擴增至少會增加 \(1\),又每次擴增複雜度是 \(O(e)\),
故複雜度是 \(O(E \vert f \vert)\)。
很爛吧。想辦法再唬爛一點?
Edmonds-Karp
有沒有試過唬爛
唬爛唬爛結果複雜度就變好了?
怎麼唬爛?
隨便做隨便唬爛
每次找一條最短的增廣路徑,沿著他增廣。
蛤?就這樣?
複雜度呢?
Edmonds-Karp 複雜度
- 結論:最多增廣 \(O(VE)\) 次!
- 小引理:每次一條邊在擴增過程中被塞滿後,\(s\) 到這條邊的距離一定會嚴格增加。
講師不想證,反正就是反證法,最後會矛盾這樣。 - \(s\) 到一條邊的距離最多是 \(V\)。
因為擴增路徑要是簡單路徑。 - 總共有 \(E\) 條邊,每條邊最多被塞滿 \(V\) 次,每次擴增 \(O(E)\)
\(\rightarrow\) 總複雜度 \(O(VE^2)\) !
比剛剛好很多了!但是能再更好嗎?
反正通常也不會用到就是了。
Dinic
前面兩個都不用會,會這個就好
繼續唬爛優化複雜度
隨便做隨便唬爛
剛剛是每次找一條最短的增廣路徑,
現在我們把所有最短的增廣路徑一口氣用完。
一次算好所有點在 \(G_r\) 上跟 \(s\) 的距離!
void bfs(){
memset(level, -1, sizeof(level));
level[s] = 0;
queue<int> q; q.push(s);
while(!q.empty()){
int u = q.front(); q.pop();
for(Edge e: G[u]){
if(e.cap > 0 and level[e.to] == -1){
level[e.to] = level[u] + 1;
q.push(e.to);
}
}
}
}DFS 的時候紀錄試過的邊!
int dfs(int u, int flow){
if(u == t) return flow;
// 下面這行是重點!
for(int &i = iter[u]; i < (int) G[u].size(); ++i){
Edge &e = G[u][i];
if(e.cap > 0 and level[e.to] == level[u] + 1){
int ret = dfs(e.to, min(flow, e.cap));
if(ret > 0){
e.cap -= ret;
G[e.to][e.rev].cap += ret;
return ret;
}
}
}
return 0;
}Dinic 複雜度
- 總共只會更新所有點的距離 \(V\) 次
一樣,簡單路徑的長度最多 \(V\) - 每次要找完所有長度為 \(k\) 的擴充路徑要 \(O(kE)\)
- 總複雜度加一加就是 \(O(V^2E)\)!
- 還可以再更好但就先這樣吧。
講師太弱只會到這邊。
再更多題目
TopCoder SRM 590
Fox And City
有 \(n \le 40\) 個點 \(1 \sim n\) ,\(m\) 條長度為 \(1\) 的無向邊,
保證這張圖是聯通的。
每一個點有一個「期望距離 \(want_i\)」,
假設點 \(i\) 與點 \(1\) 的實際距離為 \(real_i\),
失望值即為 \((want_i - real_i) ^ 2\)。
你可以對這張圖增加一些長度為 \(1\) 的無向邊,
求失望值和最小值,
以及要加上哪些邊。
注意到不需要最小化增加的邊的數量。
怎麼看都不是 Flow 對吧。
Subtitle
Subtitle
Subtitle
Subtitle
這題只能傳 Kotlin,
看看題目就好。
難題
難題
想要更多嗎?
一些注意事項
-
不要中毒
CodeForces 上面一排題目有 Flow tag 的官解一點關係都沒有(就算看起來有像也是),有時候就算是 Flow 的題目也不一定要寫出 Flow 演算法。 -
不要仲毒
-
這只是 Flow 的最最基礎的一小部分而已,還有一大堆講師不會、沒講的
-
不要中毒,很重要,不要看到就砸
耍Dinic
其實還有比 Dinic 更好的
主要不是這篇文章,是他底下的留言和超連結們。
關鍵字:Preflow-Push
實際上大多數情況還是 Dinic 快。
平面圖似乎能做到 \(O(N \log N)\)?