Problema de enrutamiento de vehículos:

Introduction

The simulated annealing algorithm was originally inspired from the process of annealing in metal work.
Annealing involves heating and cooling a material to alter its physical properties.
As the metal cools its new structure becomes fixed, consequently causing the metal to retain its newly obtained properties.

Who

Was described by Scott Kirkpatrick, C. Daniel Gelatt and Mario P. Vecchi in 1983

Useful

An engineer from General Motors applied this algorithm to their production.

The cost of production for each automobile felt around $20.

It saved millions of dollars annually.

Advantages

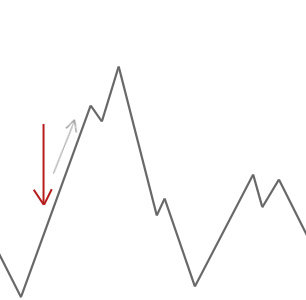
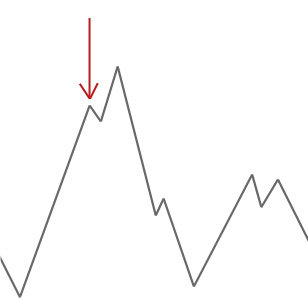
A hill climber algorithm will simply accept neighbour solutions that are better than the current solution.

When the hill climber can't find any better neighbours, it stops.

Simulated annealing works slightly differently than this and will occasionally accept worse solutions.

How does it work

First we need set the initial temperature and create a random initial solution.
Then we begin looping until our stop condition is met.
From here we select a neighbour by making a small change to our current solution.
Finally, we decrease the temperature and continue looping

Pseudoalgorithm

function SA(problem, schema) ret (solution_status)
    current_status:= INITIAL_STATUS(problem);
    T:= initial_temp(schema); top:=num_iterations(schema); t:=0;
    repeat
        inner_status:= current_status; it:=0;
        repeat
            next := random_event (inner_status);
            AE := value(next) – value(inner_status);

            if <0 then inner_status:=next;
            else q:=min{1, e-/T};

            if random(0,1)<q then inner_status:=next;
            it:= it+1;
        until it=top;
        current_status:= inner_status; T:=COOL(T, schema); t:=t+1;
    until T0
ret current_status;

Neighbours

First we check if the neighbour solution is better than our current solution.
YES: we accept it unconditionally.
NO:, We need to consider -> how much worse the neighbour solution is; and how high the current 'temperature' of our system is.
At high temperatures the system is more likely accept solutions that are worse.

Simulation 1 (c101_100)

Simulation 2 (r101_100)

Simulation 3 (rc101_100)

References

Application of Simulated Annealing to Routing Problems in City Logistics - Hisafumi Kokubugata and Hironao Kawashima, Department of Administration Engineering, Keio University
Japan
Essentials of Artificial Intelligence - Matt Ginsberg, Morgan Kaufmann Publishers Editorial

Thank you for your attention