
第七章 机械能守恒定律
第一节 功:2课时
第二节 功率:2课时
第三节 动能 动能定理:4课时
第四节 重力势能:2课时
第五节 机械能守恒定律:3课时


第一节
功
一、功

第一节
功

一个物体受到力的作用,并在力的方向上发生了位移,我们就说这个力对物体做了机械功,简称功。
一个物体受到力的作用,并在力的方向上发生了位移,我们就说这个力对物体做了机械功,简称功。

功是标量
单位:\(\rm{J}\)(焦耳),\(1{\rm{J}} = 1{\rm{N}} \cdot {\rm{m}}\)
式中,\(F\) 表示物体受到的力,\(s\) 表示物体在力的方向上发生的位移大小
一、功

第一节
功
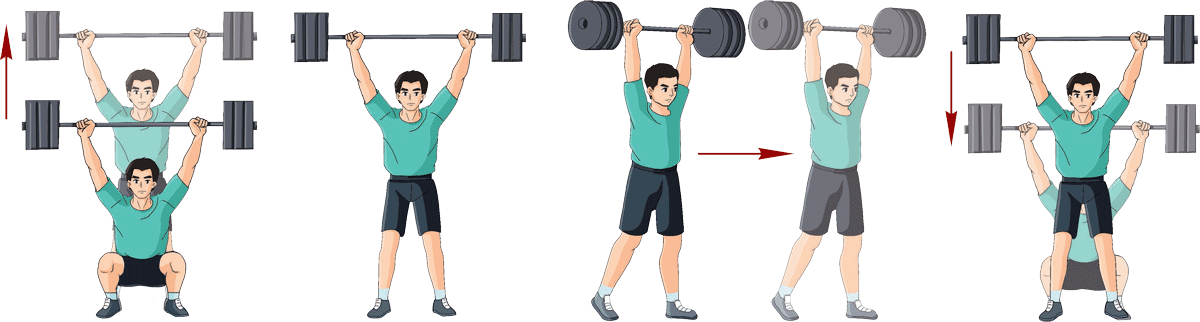
(a)
(b)
(c)
(d)
请你说说在以下四种情况中运动员都对杠铃做功吗?
二、功的计算

第一节
功
恒力对物体所做的功 \(W\) 等于恒力 \(F\) 大小、位移 \(s\) 大小、恒力与位移之间夹角的余弦 \(cos\theta\) 三者的乘积

二、功的计算

第一节
功
如图所示,用同样的力 \(F\) 拉同一物体,在甲(光滑水平面)、乙(粗糙水平面)、丙(光滑斜面)、丁(粗糙斜面)上通过同样的距离,则对于拉力 \(F\) 的做功情况,下列判断正确的是( )
(A)甲做功最少 (B)丁做功最多
(C)做功一样多 (D)无法比较
P93/3
三、正功与负功

第一节
功
当 \( \theta= \frac{\pi}{2} \) 时,\( \cos \theta=0 \),\( W=0\),这时力的方向与位移的方向垂直,力不做功。
当\(\frac{\pi}{2}<\theta≤ \pi \)时,\( \cos \theta<0 \),\( W<0\),这时力做负功,或者说物体克服力做功。
当 \( 0≤\theta<\frac{\pi}{2} \) 时,\( \cos \theta>0 \),\( W>0\),这时力做正功。
注意:虽然功有正负,但功是标量,符号并不表示方向。
三、正功与负功

第一节
功
如图,光滑斜面放在水平面上,斜面上用固定的竖直挡板挡住一个光滑的重球。当整个装置沿水平面向左匀速运动的过程中,下列说法正确的是( )
A.重力不做功
B.斜面对球的弹力不做功
C.斜面对球的弹力做正功
D.挡板对球的弹力做负功
P93/6

第一节
功
曲线运动时,恒力做的功
力 \(F\) 与力方向上位移 \(s\) 的乘积

微元法
重力做功的表达式

第一节
功

平抛运动
若物体上升 \(h\),则重力做功的表达式为

第一节
功
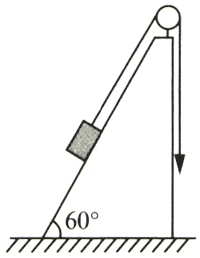
如图,某高炉的料车轨道与水平面成 60° 角,全长 80 m,车与料的总质量为 8 t。已知轨道对车的摩擦阻力为 4 000 N,料车用绳索牵引并做匀速运动。\(g\) 取 \(10 \rm{m/s^2}\),求每提升一车料时,
(1)绳索拉力所做的功;
(2)车克服重力所做的功;
(3)车克服摩擦力所做的功;
(4)轨道对车的支持力所做的功。

第一节
功
一女士站立在台阶式自动扶梯上正在匀速上楼,一男士站立在履带式自动人行道上正在匀速上楼。下列关于两人受到的力做功判断正确的是( )
A.支持力对女士做正功 B.支持力对男士做正功
C.摩擦力对女士做负功 D.摩擦力对男士做负功
四、计算总功的两种方法

第一节
功
先分别求出各力做的功,再求这些功的代数和
先求各力的合力,再求合力做的功
四、计算总功的两种方法

第一节
功
9.如图,一位质量 m = 50 kg 的滑雪运动员从高度 h = 30 m 的斜坡自由滑下(初速度为零)。斜坡的倾角 θ = 37°,滑雪板与雪面滑动摩擦因数 μ = 0.1,g 取 10 m/s2 ,则运动员滑至坡底的过程中,不计空气阻力,求:
(1)各个力所做的功分别是多少?
(2)合力做了多少功?
P99/9
四、计算总功的两种方法

第一节
功
如图所示,长度 \(l\ = 1 \rm{m} \)、质量 \(m = 5 \rm{kg}\) 的均质硬杆一端由光滑铰链固定于天花板上的 \(O\) 点。在杆的另一端施加水平恒力 \(F = 10 \rm{N}\),使杆由竖直位置绕 \(O\) 点转过角度 \(θ = 37°\),\(g\) 取 \(10 \rm{m/s^2}\),求此过程中各力对杆所做的总功。

五、功的图像表示

第一节
功

力-位置图像(示功图)
图线下的阴影面积表示在一段位移上力做的功
(变力做功仍成立)


微元法

第一节
功
五、功的图像表示
2.一物体在水平拉力 \(F\) 的作用下沿水平面运动。已知拉力 \(F\) 随物体运动位移 \(x\) 的变化情况如图,则在 0~8 m 的运动过程中,拉力 \(F\) 做的功为 ( )
A.6 J B.18 J C.20 J D.22 J
P97/2

第一节
功
例3:以前机械化生产水平较低,人们经常通过“驴拉磨”的方式把粮食颗粒加工成粗面来食用。如图,假设驴拉磨的力大小始终为 500 N,运动半径为 1 m,则驴拉磨转动一周所做的功为( )
A.0 J B.500 J C.500π J D.1 000π J

第一节
功
如图所示,质量 \(m = 30 \rm{kg}\) 的儿童从滑梯顶端 A 点滑下,经长 \(l = 12 \rm{m}\) 的旋转滑道到达底端 B 点,A、B 两点间的水平距离 \(x = 4 m\),高度差 \(h = 3 \rm{m}\)。若下滑过程中阻力 \(F_阻\) 的大小恒为 \(60 \rm{N}\),\(g\) 取 \(10 \rm{m/s^2}\)。求下滑过程中重力 \(G\) 和阻力 \(F_阻\) 对儿童所做的总功。



第二节
功率
一、功率

如何描述做功的快慢?
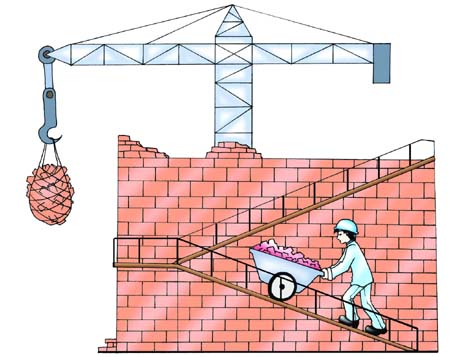

建筑工人在 1 min 内将质量为 20 kg 的水泥搬到 6 m 高的三楼;工地上的起重机在 20 s 内将质量为 1 t 的建筑材料匀速提升 10 m。比较建筑工人和起重机做功的快慢并简述理由。

第二节
功率
一、功率
功 \(W\) 跟完成这些功所用时间 \(t\) 的比值,叫做功率。

第二节
功率
单位:\(\rm{W}\)(瓦特),\(1{\rm{W}} = 1{\rm{J}/\rm{s}} \)

功率是标量
常用单位:千瓦(\(\rm{kW}\))
物理意义:描述物体做功快慢的物理量
二、平均功率和瞬时功率

第二节
功率
平均功率:
瞬时功率:

二、平均功率和瞬时功率

第二节
功率
10.一质量为 \(1 \rm{kg}\) 的小球从距地面 \(30 \rm{m}\) 的高处自由下落,\(g\) 取 \(10 \rm{m/s^2}\)。求:
(1)在前 \(2 \rm{s}\) 内重力所做的功;
(2)在前 \(2 \rm{s}\) 内重力做功的平均功率;
(3)在 \(2 \rm{s}\) 末重力做功的瞬时功率。
P102/10
二、平均功率和瞬时功率

第二节
功率
6.用水平恒力 \(F\) 作用在一个物体上,使该物体沿光滑水平面在力的方向移动距离 \(s\),\(F\) 做的功为 \(W_1\),功率为 \(P_1\);再用同样的水平力 \(F_2\) 使该物体在粗糙的水平面上在力的方向上移动距离 \(s\),\(F\) 做的功为 \(W_2\),功率为 \(P_2\)。则 ( )
A.\(W_1\) < \(W_2\),\(P_1\) > \(P_2\)
B.\(W_1\) > \(W_2\),\(P_1\) > \(P_2\)
C.\(W_1\) = \(W_2\),\(P_1\) > \(P_2\)
D.\(W_1\) < \(W_2\),\(P_1\) = \(P_2\)
P101/6

第二节
功率
三、额定功率和实际功率
额定功率:机械在正常状态下长时间工作的最大功率
实际功率:机械实际运行时的功率

第二节
功率
从 \(P = Fv\) 可以看出,汽车、火车等交通工具和各种起重机械,当发动机的输出功率 \(P\) 一定时,牵引力 \(F\) 与速度 \(v\) 成反比。
四、机车启动问题
发动机输出的功率不能无限制地增大,所以汽车上坡时司机要用“换挡”的办法减小速度,来得到较大的牵引力。


第二节
功率
四、机车启动问题
大型汽车上坡时,司机一般都将变速挡换到低速挡位上,而小型汽车上坡时,司机一般加大油门,这样做主要是为了( )
A.节省燃料 B.后者使汽车获得较大的功率
C.前者使汽车获得较小的牵引力 D.后者使汽车获得较小的牵引力
P105/1

第二节
功率
四、机车启动问题
某型号汽车发动机的额定功率为 60 kW,在水平路面上行驶时受到的阻力是 1 800 N,求:
(1)发动机在额定功率下汽车匀速行驶的速度。
(2)假定汽车匀速行驶速度为 54 km/h 时受到的阻力不变,此时发动机输出的实际功率是多少?
1、匀速行驶
匀速行驶时:
所以:


第二节
功率
四、机车启动问题
受到恒定阻力 \(f\) 的汽车以额定功率 \(P\) 启动时,我们发现随着速度 \(v\) 增大,牵引力 \(F\) 减小,原因是______________________________。从而,根据__________________________,可得加速度 \(a\) 变小,直到加速度 \(a = 0 \) 时,速度达到最大 \(v_m\)。
2、恒定功率启动
P106/9

\(v\) 增大
\(F_牵\) 减小
\(a\) 减小
最后
\(a=0\) ,速度最大 \(v_m=\frac{P}{f}\)



第二节
功率
四、机车启动问题
一列车总质量 \(M\) = 500 t,机车发动机的额定功率 \(P = 6×10^5\) W,在水平轨道上行驶时,轨道对列车的阻力 \(f\) 是车重的 0.01 倍,\(g\) 取 \(10 m/s^2\)。
(1)求列车行驶的最大速度 \(v_m\);
(2)若发动机以额定功率 \(P\) 工作,行驶速度 \(v\) = 1 m/s 时,求列车的瞬时加速度大小 \(a\);
(3)若以 36 km/h 速度匀速行驶时,求发动机的实际功率 \(P^′\);
2、恒定功率启动
P108/10




第二节
功率
四、机车启动问题
3、匀加速启动
一列车总质量 \(M\) = 500 t,机车发动机的额定功率 \(P = 6×10^5\) W,在水平轨道上行驶时,轨道对列车的阻力 \(f\) 是车重的 0.01 倍,\(g\) 取 \(10 m/s^2\)。
(4)若列车从静止开始,保持 \(0.5 \rm{m/s^2}\) 的加速度做匀加速运动,求这一过程维持的最长时间 \(t\)。


思考:之后车做怎样的运动?
思考:此过程中发动机的功率 \(P\) 如何变化?

第二节
功率
四、机车启动问题
3、匀加速启动
(多选)一辆小汽车在水平路面上由静止启动,在前 \(5 \rm{s}\) 内做匀加速直线运动,\(5 \rm{s}\) 末达到额定功率,之后保持以额定功率运动,其 \(v-t\) 图像如图。已知汽车的质量 \(m = 1×10^3 \rm{kg}\),汽车受到地面的阻力为车重的 \(0.1\) 倍,则下列说法正确的是 ( )
A.汽车在前 \(5 \rm{s}\) 内的牵引力为 \(5×10^3\) N
B.汽车速度为 \(25 \rm{m/s}\) 时的加速度为 \(3 \rm{m/s^2}\)
C.汽车的额定功率为 \(80 \rm{kW}\)
D.汽车的最大速度为 \(80 \rm{m/s}\)


第三节
动能 动能定理

第三节
动能 动能定理
一、动能
物体由于运动而具有的能量称为动能(kinetic energy)
运动物体的动能与物体的质量和速度有关,物体的质量越大,速度越大,其动能就越大。
用符号 \(E_k\) 表示
\(E_k = mv\) ???
能的单位与功的单位相同,也是焦(J)
标量,没有方向

第三节
动能 动能定理
一、动能


如何计算动能?
可以用力做的功进行量度
动能:物体质量与速度的二次方乘积的一半
结论

第三节
动能 动能定理
一、动能
7.光滑水平面上一运动的磁铁动能为 \(E_k\),若其吸引一静止的相等质量的铁球后,二者共同运动速度变为原来的一半,则总动能为 ( )
A.\(2E_k\) B.\(E_k\) C.\(\frac{E_k}{2} \) D.\(\frac{E_k}{4} \)
P110/7

第三节
动能 动能定理
一、动能

一个质量为 \(1 \rm{kg}\) 的小球,以 \(3 \rm{m/s}\) 的速度沿水平方向向墙壁运动,碰撞后以原来的速率反向弹回,则在碰撞过程中,小球的速度变化了_____m/s,动能变化了_____J。
P110/9
注意

第三节
动能 动能定理
一、动能

如何利用物体的动能?


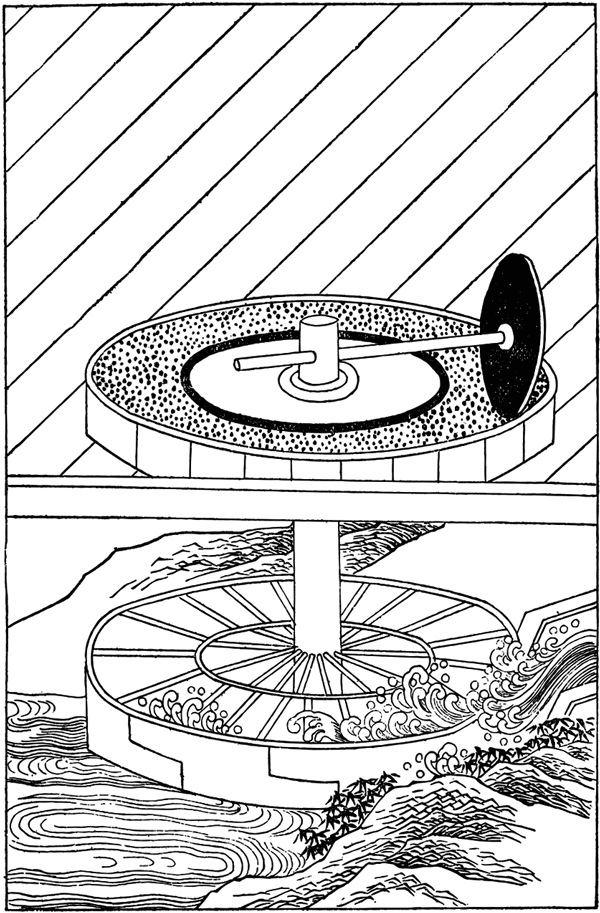
水力发电
风力发电

第三节
动能 动能定理
一、动能
5.(多选)下列各项中,属于人类利用物体的动能的实例是( )
A.自然界中海浪冲击海堤 B.流动的水推动水轮机
C.利用下落的重锤打桩 D.龙卷风把树连根拔起
P112/5

第三节
动能 动能定理
二、动能定理

物体受到的合力所做的功等于物体动能的变化量
动能定理
青出于蓝而胜于蓝
牛顿第二定律
运动学公式

第三节
动能 动能定理
二、动能定理
物体受到的合力所做的功等于物体动能的变化量
\(W_合 >0\) 时,\(\Delta E_k > 0\),表示合外力做正功,动能增加;
\(W_合 < 0\) 时,\(\Delta E_k < 0\),表示合外力做正功,动能减小
前情回顾:计算 \(W_合\) 的两种方法
先分别求出各力做的功,再求这些功的代数和(推荐)
先求各力的合力,再求合力做的功
动能定理对于变力做功和曲线运动依然成立

第三节
动能 动能定理
二、动能定理
解决高中力学问题的三把钥匙

牛顿第二定律
合力产生加速度
动能定理

合力做功改变动能
动量定理

合力的冲量改变动量

第三节
动能 动能定理
课本P84/7
如图所示,质量为 \(m\) 的物体在水平拉力 \(F\) 的作用下,由静止开始沿粗糙水平面向前运动 \(s_1\) 后,撤去拉力 \(F\) 已知物体与水平面间的摩擦力为 \(F_f\)。求:
(1)刚撤去拉力时,物体的速度 \(v\);
(2)物体滑行的最大距离 \(s_2\)。

解:(1)
(2)

牛顿第二定律
解:(1)
(2)

动能定理

第三节
动能 动能定理
P115/9
9.某人将一个质量为 2 kg 的物体从高 10 m 处以 10 m/s 的初速度水平抛出,落地时速度的大小为 12 m/s.则人在抛物体的过程中所做的功为__________ J,物体在飞行过程中,空气阻力对物体做的功为__________ J。(\(g\) 取 \(10 \rm{m/s^2}\))
可以解决变力做功问题


第三节
动能 动能定理
可以解决变力做功问题
3.一个质量为 2 kg 的物体在空中从静止开始下落,受到的空气阻力与速度的关系为 \(f = 0.5v^2\),下落 20 m 高度时速度已达最大,则这一过程克服空气阻力做的功为(\(g\) 取 \(10 \rm{m/s^2}\)) ( )
A.360 J B.400 J C.300 J D.40 J

第三节
动能 动能定理
可以解决曲线运动的过程
如图所示,长 \(l = 1 \rm{m}\) 的轻质细绳下端悬挂质量 \(m = 1 \rm{kg}\) 的钢球,对钢球施加水平恒力 \(F = 10 \rm{N}\),将小球从最低点 A 由静止开始拉动,且拉动过程中细绳始终绷直。若不计空气阻力,\(g\) 取 \(10 \rm{m/s^2}\),求:
(1)细线转过 \(θ = 30°\) 时,钢球的速度大小 \(v_1\);
(2)细线转过的最大角度?
课本P68/6


第三节
动能 动能定理
处理过程较复杂的问题时有明显的优越性
如图,一质量为 \(m\) 的小球自松软泥土的地面上方高为 \(h\) 处自由下落,小球最终陷入泥土的深度为 \(d\),不计空气阻力,重力加速度为 \(g\),则泥土对小球的平均阻力大小为( )
A.\(\frac{mgh}{d}\) B.\(\frac{mg(h + d)}{d}\) C.\(\frac{mgd}{h}\) D.\(\frac{mg(h + d)}{h}\)
P115/5
解:前半段自由落体运动
后半段,匀减速直线运动

牛顿第二定律

第三节
动能 动能定理
二、动能定理
预备知识
1、计算 \(W\) 的两种方法
先分别求出各力做的功,再求这些功的代数和
先求各力的合力,再求合力做的功
2、计算 \(W\)


第四节
重力势能

第四节
重力势能
由于物体高度改变而变化的能量叫做重力势能(gravitational potential energy),用 \(E_p\) 表示


如图所示,在水平桌面上铺一块厚薄均匀的泡沫板,让半径相同、质量不同的实心小球从不同的高度自由下落到泡沫板上,根据撞击产生凹痕的深浅猜想小球的重力势能与哪些因素有关。
结论:质量 \(m\) 越大,高度 \(h\) 越大,重力势能越大
\(E_p = mh\) ???

第四节
重力势能
一、重力做功的特点

重力是恒力,根据恒力做功的计算式
-
质量为 \(m\) 的物体沿任意路径由 A 运动到 B
重力做功与路径无关,仅取决于始、末位置
-
质量为 \(m\) 的物体沿任意路径由 B 运动到 A

第四节
重力势能
一、重力做功的特点

保守力:做功与路径无关,只取决于始、末位置,如重力、弹簧弹力、万有引力……
耗散力:做功与路径有关,如空气、水等流体的阻力

第四节
重力势能
一、重力做功的特点
如图,一位小朋友分别从斜梯、旋梯和直杆的顶端滑到地面,则( )
A.沿直杆下滑时,重力做的功最小
B.沿旋梯下滑时,重力做的功最大
C.无论沿哪个路径下滑,重力做的功都一样
D.条件不足,无法判断重力做功的大小
P121/1

第四节
重力势能
二、重力势能
可以用重力做的功进行量度

结论:
注意:重力势能是物体和地球这一体系所共有的。只是为了简单起见,我们说物体具有重力势能

第四节
重力势能
二、重力势能
高度具有相对性,但高度差是绝对的


珠穆拉玛峰,海拔高度为 \(h = 8844 \rm{m}\)
吐鲁番盆地艾丁湖,海拔高度 \(h = -161\rm{ m}\)
高度差 \(\Delta h =9005 m\)
- 高度正值比负值大
- 通常取海平面为零高度位置
- 高度是相对的,与零高度选取有关
- 高度差是绝对的,与零高度选取无关

第四节
重力势能
二、重力势能
-
由于高度 \(h\) 具有相对性,所以重力势能也是相对的,只有在选取了重力势能为零的参考平面以后才能确定重力势能。
-
物理学中将重力势能为零的参考平面称为零势能面,\(h\) 就是物体相对于零势能面的高度。零势能面一般都是根据研究需要设定的。
-
若物体处于零势能面以上,则 \(h > 0\),\(E_p > 0\);处于零势能面以下,则 \(h < 0\),\(E_p < 0\)。
可以用重力做的功进行量度

第四节
重力势能

如图所示,树上与 A 等高的 P 处有一个质量 m = 0.3 kg的苹果下落。求:
(1)以 A 所在水平面为零势能面,求 P 处苹果的重力势能 \(E_p\);
(2)以 C 所在水平面为零势能面,求 P 处苹果的重力势能 \(E_p\);
(3)苹果由 P 落至 D 的过程中,苹果重力势能的变化量 \(\Delta E_p\) ;
(4)苹果由 P 落至 D 的过程中,求重力所做的功 \(W_G\)。

第四节
重力势能
三、重力做功与重力势能变化量的关系
注意:重力势能取决于零势能面位置的选取,但重力势能的变化量与零势能面的选取无关
重力势能变化量
物体下降,重力做正功,\(W_G > 0\),物体重力势能减少,\(ΔE_p < 0\);
物体上升,重力做负功或物体克服重力做功,\(WG < 0\),物体重力势能增大,\(ΔE_p > 0\)。

第四节
重力势能
三、重力做功与重力势能变化量的关系
如图,总长为 \(2 \;\rm{m}\) 的光滑匀质铁链,质量为 \(10 \;\rm{kg}\),跨过一光滑的轻质定滑轮。开始时铁链的两底端相齐,当略有扰动时某一端开始下落,\(g\) 取 \(10 \;\rm{m/s^2}\),则从铁链刚开始下落到铁链刚脱离滑轮这一过程中,重力对铁链做了多少功?重力势能如何变化?
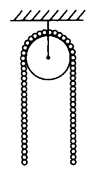
P126/10

第四节
重力势能
四、弹性势能


发生弹性形变的物体由于各部分之间相对位置发生变化而具有的能量叫做弹性势能(elastic potential energy)。
在弹性限度内,形变量越大,劲度系数越大,弹性势能越大。

第四节
重力势能
四、弹性势能
弹力做正功,\(W_弹 > 0\),弹性势能减少,\(ΔE_p < 0\);
弹力做负功或物体克服弹力做功,\(W_弹 < 0\),弹性势能增大,\(ΔE_p > 0\)。
与重力做功和重力势能变化量的关系完全相同

第四节
重力势能
四、弹性势能
如图,在光滑的水平面上有一物体,它的左端连一弹簧,弹簧的另一端固定在墙上,在力 \(F\) 作用下物体处于静止状态。当撤去 \(F\) 后,物体将向右运动,在物体向右运动过程中,下列说法正确的是( )
A.弹簧的弹性势能逐渐减小
B.弹簧的弹性势能逐渐增大
C.弹簧的弹性势能先增大再减小
D.弹簧的弹性势能先减小再增大
P125/3



第五节
机械能守恒定律
前情回顾
功
功率
能
与形变量、劲度系数有关,公式不做要求
功是能量转化的量度

第五节
机械能守恒定律


第五节
机械能守恒定律
一、机械能 机械能的转化
动能、势能统称为机械能
动能和重力势能之间的相互转化
曲线运动
自由落体运动
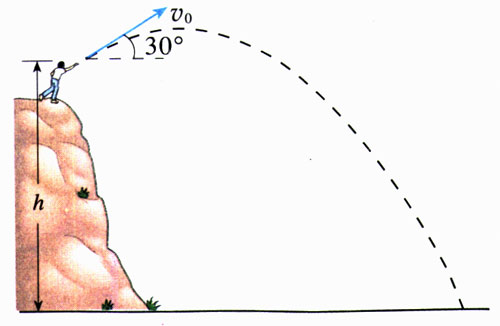
抛体运动

第五节
机械能守恒定律
一、机械能 机械能的转化
动能、势能统称为机械能


动能和重力势能之间的相互转化
动能、重力势能和弹性势能之间的相互转化

第五节
机械能守恒定律

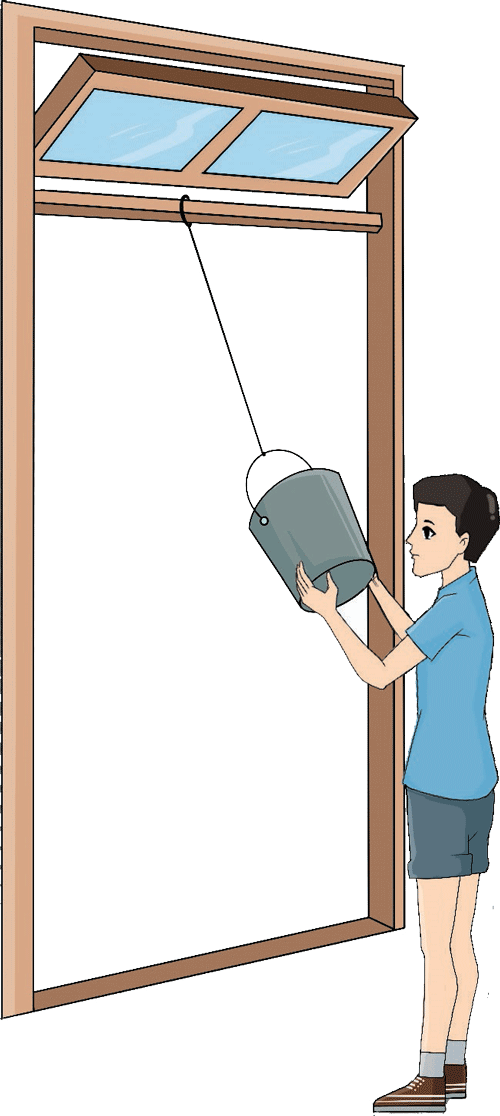
如图所示,在一个提桶内放一些重物,用绳子将它悬挂在门框下。将提桶拉离竖直位置并凑近自己的鼻子后放手,提桶将前后摆动。如果放手后站着不动,提桶在摆动过程中是否会碰到鼻子呢?请尝试一下。

一、机械能 机械能的转化

第五节
机械能守恒定律
二、机械能守恒定律
在只有重力和弹力做功的系统内,动能与势能相互转化,机械能总量不变。这就是机械能守恒定律。
理论推导
由动能定理:
将重力所做的功 \(W_G\) 、弹力所做的功 \(W_E\) 分离出来,并用 \(W'\) 表示除重力和弹力以外其他力所做功的代数和
根据重力、弹力做功的特点,用 \( \Delta E_p\) 表示重力势能与弹性势能变化量的代数和
即
若 \(W' = 0\),则 \(\Delta E = 0\)

第五节
机械能守恒定律
二、机械能守恒定律
守恒条件:只有重力(和弹力)做功
物体只受重力
除重力外还受其他力,但其他力不做功


自由落体运动
抛体运动
接触面光滑
不计空气阻力

第五节
机械能守恒定律
二、机械能守恒定律
下列过程中,机械能一定守恒的是( )
A.子弹射穿木块的过程
B.树叶在空中缓缓飘落的过程
C.木箱沿固定的光滑斜面向上滑动的过程
D.跳伞运动员张开伞后,在空中匀速下降的过程
P127/例1

第五节
机械能守恒定律
二、机械能守恒定律
表达式:

或

第五节
机械能守恒定律
二、机械能守恒定律
p128/例3
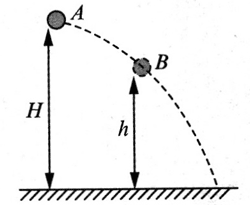
(多选)如图,质量为 \(m\) 的物体,以速度 \(v_A\) 从离地为 \(H\) 的 A 点抛出,当它落到距离地面高为 \(h\) 的 B 点时,速度为 \(v_B\),在不计空气阻力的情况下,下列说法正确的是(取地面为零势能面)( )
A.物体在 A 点的机械能是 \(mgh + \frac{1}{2}mv{_B^2}\)
B.物体在 B 点的机械能是 \(mgh + \frac{1}{2}mv{_B^2}\)
C.物体着地时的机械能是 \(mgh + \frac{1}{2}mv{_A^2}\)
D.物体着地时的机械能是 \(mgH + \frac{1}{2}mv{_A^2}\)

第五节
机械能守恒定律
二、机械能守恒定律
p129/10
如图,一质量为 60 kg 的探险者在丛林探险,为了从一绝壁到达水平地面,探险者将一根粗绳缠绕在粗壮树干上,拉住绳子的另一端,从绝壁边缘的 A 点由静止开始荡向低处,到达最低点 B 时脚恰好触到地面,此时探险者的重心离地面的高度为 0.5 m。已知探险者在 A 点时重心离地面的高度为 8.5 m。以地面为零势能面,不计空气阻力,\(g\) 取 \(10 \;\rm{ m/s^2}\)。探险者可视为位于其重心处的一个质点。求:
(1)探险者在 A 点时的重力势能;
(2)探险者运动到 B 点时的速度大小;
(3)探险者运动到重心离地面 5 m 高处时的机械能。

第五节
机械能守恒定律
二、机械能守恒定律
\(W'\) 表示除重力和弹力以外其他力所做功的代数和
若 \(W' = 0\),则 \(\Delta E = 0\)
若 \(W' > 0\),则 \(\Delta E > 0\),其他形式能转化为机械能
若 \(W' < 0\),则 \(\Delta E < 0\),机械能转化为其他形式能
如果除了重力和弹力外,还有其他外力对物体做功或物体克服其他外力做功,机械能的总量将发生变化,这时机械能__不守恒___(选填“守恒”或“不守恒”),机械能和其他形式的能量将发生__转换(转化)__。
物体在地面附近以 \(2\; \rm{m/s^2}\) 的加速度匀减速竖直上升,则在上升过程中,物体的动能将__减小_,物体的机械能将_增大_。(均选填“增大”“减小”或“不变”)

第五节
机械能守恒定律
二、机械能守恒定律

在光滑水平面上做匀速圆周运动的物体机械能是否守恒?
解答:在光滑水平面上做匀速圆周运动的物体动能和重力势能都不变,没有发生动能和重力势能之间的能量转化、转移,虽然其机械能的大小保持不变,但不符合机械能守恒的条件。


第五节
机械能守恒定律
二、机械能守恒定律
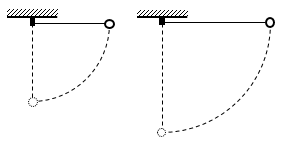
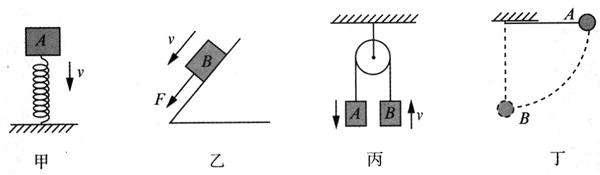
(多选)如图,下列关于机械能是否守恒的判断正确的是( )
A.图甲中,物体 A 将弹簧压缩的过程中,物体 A 的机械能守恒
B.图乙中,物体 B 在大小等于摩擦力的拉力作用下沿斜面下滑时,机械能守恒
C.图丙中,不计任何阻力时 A 加速下落、B 加速上升的过程中,A、B 组成的系统机械能守恒
D.图丁中,小球由水平位置 A 处静止释放,运动到 B 处的过程中,机械能守恒
P130/5

第五节
机械能守恒定律
二、机械能守恒定律
如图,ACB 为一光滑的斜面,ADECFB 为一光滑曲面,BB1 为一水平面,A 点离地面高为 h,E 点离地面高为 0.6h,C 点离地面高为 0.5h,D 点离地面高为 0.2h,AB 与水平面的夹角为 θ。一质量为 m 物体从静止开始沿 ACB 斜 面滑下。(选取地面为零势能面)
(1)求物体到达 B 点的速度大小;
(2)若物体从静止沿 ADECFB 曲面下滑,求到达 C 点的速度大小,并求到达 D 点的机械能为多少;
(3)在 B 点至少有多大的初动能才能使物体沿 BFCEDA 曲面到达 D 点。
P134/11


第五节
机械能守恒定律
三、验证机械能守恒定律
一切机械能守恒的过程都可以用来验证机械能守恒定律


证明任意位置 \(mgh + \frac{1}{2}mv^2\) 相同

第五节
机械能守恒定律
三、验证机械能守恒定律
证明任意位置 \(mgh + \frac{1}{2}mv^2\) 相同

第五节
机械能守恒定律
三、验证机械能守恒定律

实验器材

第五节
机械能守恒定律
三、验证机械能守恒定律

实验器材

第五节
机械能守恒定律
三、验证机械能守恒定律
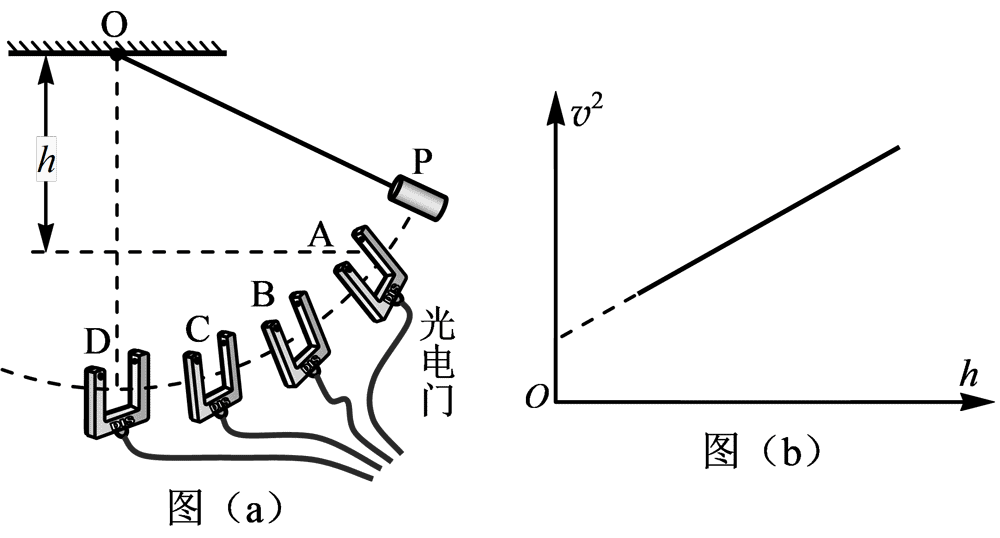
实验原理
- 由于连接杆的质量远小于摆锤质量,摆动过程中,连接杆的动能和重力势能可忽略,只要测量摆锤的动能和重力势能即可。
- 摆锤速度的测量:摆锤内置的光电门传感器可以测出摆锤经过每个挡光片的时间,进而得到摆锤的瞬时速度。
- 摆锤高度的测量与改变:6 块挡光片可用螺栓固定在不同位置并由板上刻度读出对应的高度,刻度对应的高度是光电门经过该位置时光孔(即挡光片上十字刻纹)的高度,相邻光孔之间的高度差为 0.5 cm。

第五节
机械能守恒定律
三、验证机械能守恒定律
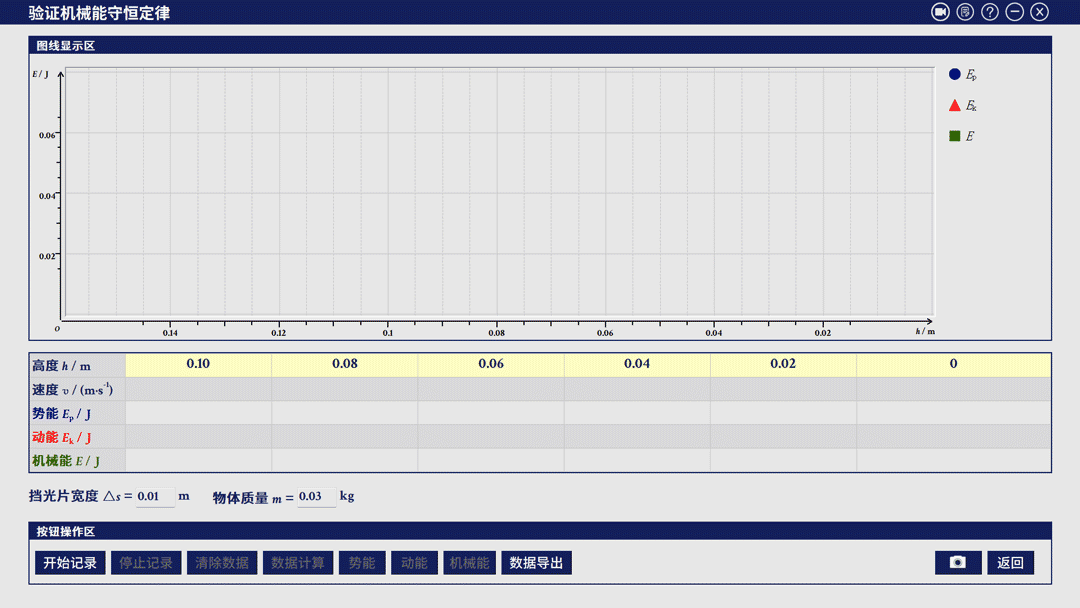
实验数据处理

第五节
机械能守恒定律
三、验证机械能守恒定律
误差分析
实验中摆锤在各位置的重力势能和动能不同。但重力势能与动能变化的趋势相同,且两者之和近似不变。仔细思考可能会发现,机械能在摆锤向下摆动过程中逐渐减小。想想这是为什么?