
第三章 相互作用与力的平衡
在本章中我们将:
1.认识和理解位移、速度、加速度等物理量。
2.经历质点模型的建构过程,初步学会测量物体的瞬时速度。
3.学习用文字、关系式、图像描述简单的实际运动。


第一节
生活中常见的力

第一节
生活中常见的力
零、八年级第一学期 第三章 第三节 力
-
力(force):物体与物体之间的相互作用
-
力的作用效果:1、改变物体的运动状态;2、使物体发生形变
-
力的三要素:大小、方向、作用点


第一节
生活中常见的力
一、重力
物体在地面附近由于地球的吸引而受到的力称为重力(gravity),用字母 \(G\) 表示。


-
作用点:重心(center of gravity)
形状规则、质量分布均匀的物体,重心就在它的几何中心
-
大小:
-
方向:竖直向下

第一节
生活中常见的力
一、重力

如果物体的形状规则,它的重心一定在几何中心吗?物体的重心一定在物体上吗?你有什么办法找到物体的重心?
.jpg)
重心可以不在物体上

“悬挂法“确定重心

第一节
生活中常见的力

人站立在教室地板上,我们并没有观察到地板形变,人与地板间却有弹力存在。物体发生形变是否就一定存在弹力?弹力是否一定引起形变?
二、弹力
通常所说的绳子的拉力、桌面的支持力、重物对地面的压力都属于弹力。
生活经验可知,弹力与形变直接相关

第一节
生活中常见的力
二、弹力
弹性形变:撤去力后能恢复原状的形变

弹性形变

非弹性形变

第一节
生活中常见的力

二、弹力
把一支激光笔A固定在支架上,激光束分别经过平面镜B和C的反射后射到天花板,形成一个光斑。现在桌面上放一重物M,观察光斑D位置的变化。
观察微小形变

发生弹性形变的物体,由于要恢复原状,会对引起形变的物体施加力的作用,这种力称为弹力(elastic force)。
二、弹力
-
作用点:物体与物体接触的点或面上
-
方向:指向发生弹性形变物体恢复原状的方向
- 绳:沿绳
- 支持面:垂直于支持面

-
产生条件:1、接触;2、接触处有形变(挤压)

第一节
生活中常见的力
二、弹力

如图所示,质量均匀分布的木棒一端被竖直的弹性绳悬吊,另一端搁在水平地面上。木棒除了受到重力外还受到几个弹力的作用?说说这些弹力的施力物体,并画出木棒所受弹力的示意图。
示例

第一节
生活中常见的力
二、弹力


1
如图所示,将薄板曲端垫高后把一个水球放在板上。可以看到板和球都发生了形变,球和板之间有相互作用的弹力。在图上作出这对弹力的示意图,并说明它们分别是哪个物体发生形变产生的。

第一节
生活中常见的力
二、弹力
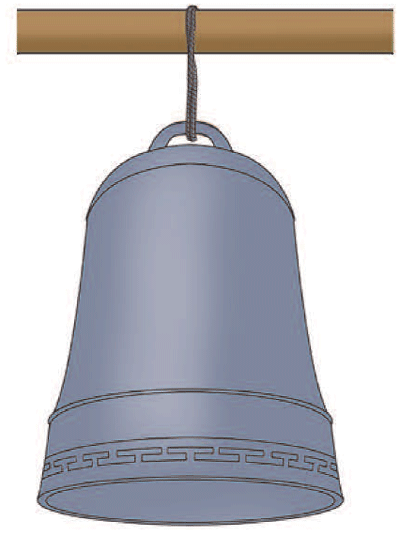

2
在我国古代钟楼中会悬挂大钟,每天用钟声来报时。大钟被悬挂在钟楼的横梁上,请分析钟所受弹力的方向,以及这个弹力是由哪个物体形变产生的。

第一节
生活中常见的力
二、弹力


4
如图所示,有四个球处于静止状态,O为球的球心,图(a)、(b)、(c)中球的球心与重心C重合,图(d)中球心O与重心C不重合。画出四个球所受弹力的示意图,并标出弹力的方向和作用点。

第一节
生活中常见的力


第一节
生活中常见的力
二、弹力
探究弹簧弹力与形变量的关系
提出问题
弹簧弹力的大小与弹簧的形变量有什么关系
实验原理
重物所受重力与弹簧的弹力大小相等
实验方案
分别测量悬挂不同重物时弹簧的形变量并记录相应重物所受到的重力
实验装置
如右图

第一节
生活中常见的力
二、弹力
探究弹簧弹力与形变量的关系
数据收集
| 实验序号 | 钩码重力 | 弹簧长度 | 弹簧形变量 |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
数据分析



第一节
生活中常见的力
二、弹力
胡克定律(Hooke's law)
在一定条件下,弹簧发生弹性形变时弹力的大小 \(F\) 与弹簧形变量的大小 \(x\) 成正比,即
\(k\) 称为弹簧的劲度系数(stiffness coefficient)
单位:牛顿/米,N/m

第一节
生活中常见的力
三、摩擦力(friction force)
两个相互接触的物体
发生相对运动时
具有相对运动趋势时
就会在接触面上产生
阻碍相对运动的
阻碍相对运动趋势的
滑动摩擦力
(sliding friction force)
静摩擦力
(static friction force)

第一节
生活中常见的力
三、摩擦力(friction force)

实例分析
父亲轻轻地沿水平方向推箱子,箱子仍相对于地面静止。
大小:
方向:
作用点:

第一节
生活中常见的力
三、摩擦力(friction force)


将木块放在水平长木板上,用力传感器(测量力的大小)沿着水平方向拉木块。开始阶段木块是静止的。当拉力达到某一数值时,木块将开始运动。开始移动前,木块在水平方向上处于二力平衡的状态,因此力传感器所采集的力的大小数据就等于静摩擦力的大小。逐渐增大拉力,描述你所看到的现象。

第一节
生活中常见的力
三、摩擦力(friction force)
1、静摩擦力的大小将随拉力的增大而增大
2、静摩擦力的增大有一个限度,它的最大值称为最大静摩擦力,它的大小等于木块刚被拉动时拉力的大小
3、通常滑动摩擦力的大小略小于同等压力下的最大静摩擦力

第一节
生活中常见的力
三、摩擦力(friction force)
滑动摩擦力的大小与接触面的材料、粗糙程度等因素有关,且与压力成正比。如果用 \(F_f\) 表示滑动摩擦力的大小,用 \(F_N\) 表示压力的大小,则有
\( \mu \) :动摩擦因数(dynamic friction factor)。

第一节
生活中常见的力
三、摩擦力(friction force)
\( \mu \) :是两个力大小的比值,无单位。
与相互接触的两个物体的材料、接触面的情况(如粗糙程度)等因素有关
注意:与接触面积、运动速度无关
| 材料 | 动摩擦因数 |
|---|---|
| 木—金属 | 0.20 |
| 木—木 | 0.30 |
| 钢—钢 | 0.25 |
| 钢—冰 | 0.02 |
| 木头—冰 | 0.03 |
| 橡胶轮胎—路面(干) | 0.71 |
\( \mu \)

第一节
生活中常见的力
三、摩擦力(friction force)


5
如图所示,某人沿粗糙水平地面用水平向右的力推着木箱沿直线向右匀速运动,人在此过程中没有出现脚底打滑的现象。分别分析地面对木箱和人的摩擦力的方向。


第一节
生活中常见的力
三、摩擦力(friction force)
情景分析1
一物体放在水平传送带上随传送带一起匀速运动

物体在运动方向上一定受到力的作用吗?

第一节
生活中常见的力
三、摩擦力(friction force)
情景分析2
一物体放在倾斜传送带上随传送带一起匀速运动

运动的物体可能受到静摩擦力作用吗?
静摩擦力的方向可能与物体运动方向相同吗?

第一节
生活中常见的力
三、摩擦力(friction force)
情景分析3
静止的物体可能受到滑动摩擦力作用吗?

此手不动
A
物体A用绳连接在墙上,拖动下面的木板,判断A所受的摩擦力方向。

第一节
生活中常见的力
三、摩擦力(friction force)
情景分析4
滑动摩擦力的方向可能与物体运动方向相同吗?

A
物体A放置在木板上,拖动下面的木板,且木板的速度 \(v_1\) 大于A的速度 \(v_2\)。判断A所受的摩擦力方向。

第一节
生活中常见的力
三、摩擦力(friction force)

示例
如图所示,用水平方向的力 \( F \) 将重为 \( G \) 的木块压在竖直的墙壁上,开始时木块保持静止。
(1)增大压住木块的水平力 \( F \) ,木块所受的摩擦力将如何变化?
(2)减小压住木块的水平力 \( F \) ,木块所受的摩擦力将如何变化?

第一节
生活中常见的力
三、摩擦力(friction force)
用大拇指和食指捏着一个装有半瓶水的开口向上的瓶子,保持静止。
(1)此时瓶子受到了哪些力的作用?


2
(2)不断地向瓶子里加水,直至瓶子充满水,整个过程中瓶子没有下滑。在此过程中,瓶子受到的各个力的大小是如何变化的?

第一节
生活中常见的力
四种基本的相互作用

引力相互作用
电磁相互作用
强相互作用
弱相互作用
重力
弹力
摩擦力

第二节
力的合成


第二节
力的合成



第二节
力的合成
一、共点力
作用于物体上同一点或力的作用线可以相交于同一点。这样的力称为共点力(concurrent force)


1
如图所示,三个物体均受到同一平面内三个力的作用。判断其中哪些属于共点力。

第二节
力的合成

初中物理知识的复习
同向一直线:
反向一直线:

第二节
力的合成
物体同时受到几个力的作用时,我们可以用一个力来替代这几个力,使这个力产生的效果与几个力同时作用的效果相同。这个力就称为合力(resultant force),而原来的几个力称为这个合力的分力(force components)。
求几个力的合力的方法称为力的合成(composition of forces)。
二、力的合成

第二节
力的合成
二、力的合成

如何求两个非一直线上的共点力的合力?
等效替代

大人单手就能提起

两个小孩同时用力提起水桶
100 N
100 N
= 200 N?

第二节
力的合成
二、力的合成
探究两个互成角度的力的合成规律


小猩猩用单臂或双臂都能将自己悬挂

第二节
力的合成
用图钉将白纸固定在图板上。在图板上再固定一枚图钉,带绳套的橡皮筋一端固定在图钉上。
弹簧测力计必须保持水平,且需调零。
1
图钉
图钉
图钉
探究两个互成角度的力的合成规律

第二节
力的合成
探究两个互成角度的力的合成规律
两个同学合作,用两个弹簧测力计互成角度地在纸面内拉橡皮筋,同时记录两个弹簧测力计的示数\(F_1\)、\(F_2\),以及两根细绳的方向及结点位置O。
2


O
\(F_1\)=2.4 N,\(F_2\)=1.8 N

第二节
力的合成
探究两个互成角度的力的合成规律
用一个弹簧测力计通过细绳套拉橡皮筋使结点到O,记录弹簧测力计的示数和细绳的方向。
3

O
\(F_1\)=2.4 N,\(F_2\)=1.8 N
\(F\)=3.6 N

第二节
力的合成
探究两个互成角度的力的合成规律
选取合适标度,用力的图示法画出 \(F_1\)、\(F_2\) 的大小与方向;
用三角板推平行线,得平行四边形,画出对角线取长度,由标度求出 \(F'\) 的大小;
用力的图示法画出 \(F\) 的大小与方向。
4
O
\(F_2\)=1.8 N
1 N
\(F_1\)=2.4 N
\(F\)=3.6 N
\(F\)‘=3.5 N

第二节
力的合成
三、平行四边形定则
两个共点力 \(F_1\) 、 \(F_2\) 的合力 \(F\) 可以用以这两个力为邻边构成的平行四边形的对角线表示。这就是力的平行四边形定则( parallelogram rule)。


第二节
力的合成
平行四边形求和的方法适用于一切矢量的求和。我们学过的位移、速度、加速度也是矢量,它们的合成也遵循平行四边形定则求和的方法
某同学从花园里的 A 点出发,沿着小路先到达 B 点,再到达终点 C,求全过程位移 \(x_{AC}\)

\(x_{AC}\)
\(x_{BC}\)
\(x_{AB}\)
\(x_{AC}\)
\(x_{BC}\)
\(x_{AB}\)
\(x_{AC}\)
三、平行四边形定则

第二节
力的合成
三、平行四边形定则


2
如图所示,质点O受两个力的作用,通过作图求出图中两个已知力的合力。


第二节
力的合成
示例 两位学生同时用水平力推一个木箱使其沿直线移动,一位用力 300 N,另一位用力 400 N,两个水平推力的夹角是 90°,求这两个力的合力的大小与方向。



第二节
力的合成
1、两力合成的合力大小范围
2、在分力大小保持不变的情况下,两分力的夹角越大,合力越小。

第二节
力的合成
如图所示,平面上有 5 个力作用在 O 点,O 点和各力的矢量终点恰好各位于一个正六边形的顶点,这 5 个力中最小的力是 1 N 。
-
先选择对称的力为分力作平行四边形来求5个力的合力;
-
再以互相垂直的力为分力作平行四边形来求5个力的合力。
比较两次的结果。

5



第三章 相互作用与力的平衡
学生实验
探究两个互成角度的力的合成规律
二
探究弹簧弹力与形变量的关系
一
探究弹簧弹力与形变量的关系
一

在铁架台的横杆上固定弹簧,组成实验装置。
1
2
用直尺测量未挂钩码时弹簧的长度 \(x_0\),并记录在数据表中。
探究弹簧弹力与形变量的关系
一

3
4
在弹簧下端挂上钩码,手托钩码慢慢向下移动,直到手离开钩码。在钩码处于静止状态时测量弹簧长度 \(x_1\) ,并记录在数据表中。
改变钩码数量,重复步骤(3)。
探究弹簧弹力与形变量的关系
一
弹簧原长 \(x_0\) = _____m
实验序号
1
…
2
钩码的质量
\(m/\rm{kg}\)
钩码受到的重力
\(G/\rm{N}\)
弹簧的形变量
\(x/\rm{m}\)
悬挂钩码后弹簧的长度
\(x_1/\rm{m}\)
0.05
0.10

5
10
3
1
2
0.49
0.98
…
…
探究两个互成角度的力的合成规律
二
实验数据记录
实验序号
\(F_1 / \rm{N}\)
\(F_1\)与\(F_2\)夹角\(\theta\)
\(F_2 / \rm{N}\)
\(F / \rm{N}\)
\(F ʹ\)与\(F\)夹角\(\theta ʹ\)
\(F ʹ/ \rm{N}\)
1
3
2

第三节
力的分解


第三节
力的分解
一、力的分解
力的合成:已知分力求合力
逆运算
力的分解:已知合力求分力

第三节
力的分解
把一个力用几个同时作用的力来替代的方法称为力的分解。
一、力的分解
力的合成的逆运算。仍符合平行四边形定则。

第三节
力的分解
一、力的分解

1

如图所示,一个 15 N 的力沿 OA 方向,它的一个分力沿 OB 方向,大小为 6 N。作图表示另一个分力的大小和方向。
启示
已知一个分力的大小和方向,力的分解有确定解

第三节
力的分解
一、力的分解

2
将一个大小等于 20 N的力,分解为两个力,其中一个分力的大小为 16 N,另一个分力的大小为 12 N。作图分析,说明满足上述条件有几种可能性。
启示
已知两个分力的大小,力的分解可能有多解

第三节
力的分解

克服阻力前进的效果
把轮胎上提的效果
二、实例分析
根据力的实际作用效果确定分力的方向
启示
已知两个分力的方向,力的分解有确定解

第三节
力的分解
二、实例分析

如图所示,一人通过箱带拉着一个旅行箱前进。拉力大小为 12 N,箱带与水平面夹角为 30° ,求拉力的水平分力和竖直分力的大小。

3
效果1
效果2

第三节
力的分解
二、实例分析

把一个木箱放在倾角为 \(θ\) 的斜面上,木箱受到重力的作用。从力的作用效果来看,应该怎样分解重力?分力的大小与斜面的倾角有什么关系?
3
\(\theta \) 增大时,\(F_1\) 增大,\(F_2\) 减小
画
算
变

第三节
力的分解
二、实例分析

如图所示,光滑斜面上物体受到的重力 \(G\) 被分解为 \(F_1\)、\(F_2\) 两个力。判断下列说法是否正确,并简述理由。
(1) \(F_1\) 是斜面作用在物体上使物体下滑的力,\(F_2\) 是物体对斜面的压力。
(2)物体受到 \(G\)、\(F_N\) 、\(F_1\) 、\(F_2\) 四个力作用。
(3)物体只受重力 \(G\) 和弹力 \(F_N\) 的作用。
(4)力 \(F_N\) 、\(F_1\) 、\(F_2\) 三个力的作用效果和 \(G\)、\(F_N\) 两个力的作用效果相同。

第三节
力的分解
二、实例分析
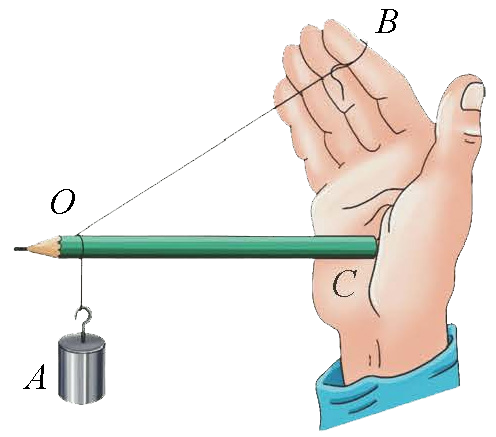
铅笔、细线把一个钩码按如图所示的方式悬挂起来,求钩码对O点的拉力 \(F\) 的分力。
4

第三节
力的分解
二、实例分析

如图所示,一辆货车陷入了泥沼,司机会找一棵结实的大树,用钢索将车A与大树B连接,拉紧;然后,只要将一根绳子绕过钢索中央的O点,沿着垂直于钢索的方向拉绳;仅需一两人之力,就能让车前进一些。
分力可以大于合力吗?
5


第三节
力的分解
二、实例分析
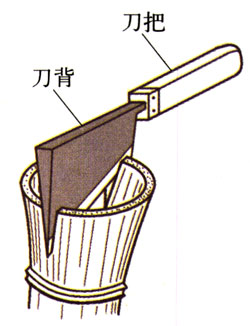
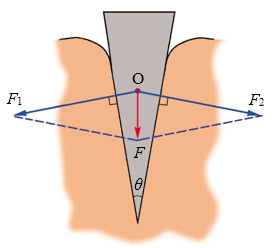
如图所示是刀刃的横截面,\(F\) 是作用在刀背上的力,画出\(F\) 的分力。
6

第四节
共点力的平衡


第四节
共点力的平衡
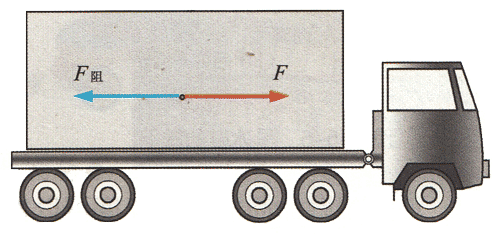

初中物理知识的复习

第四节
共点力的平衡
一、平衡状态
物体保持静止或者做匀速直线运动,就处于平衡状态。
两力平衡条件
两个力大小相等、方向相反、作用在一直线上。
这两个力的合力为零,即 \( F_合 = 0 \)

第四节
共点力的平衡
二、共点力作用下物体的平衡条件


1
受力分析
2
由两力平衡条件列式
1
受力分析
平衡条件是什么?

第四节
共点力的平衡
二、共点力作用下物体的平衡条件

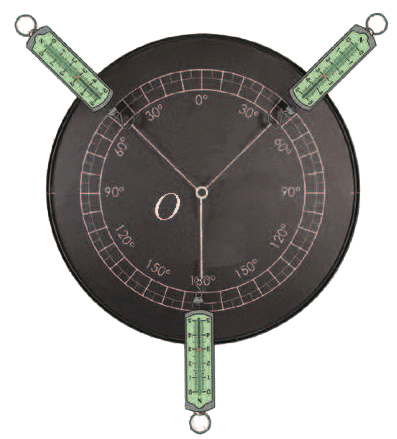
如图所示,用三个平行于桌面的弹簧测力计拉一个小环 O,使环静止。记录三个力的大小和方向,过 O 点画出力的图示。验证这三个力的合力是否为零。

第四节
共点力的平衡
二、共点力作用下物体的平衡条件
物体在共点力作用下处于平衡状态的条件是合力为零,即
推论
在三个共点力平衡的情况中,其中两个力的合力必然与第三个力大小相等,方向相反。
在 \(n\) 个共点力平衡的情况中,其中任意 \( (n-1) \) 个力的合力,必然与剩下的一个力大小相等,方向相反。

第四节
共点力的平衡
二、共点力作用下物体的平衡条件
例题1
【多选】一个物体在许多个共点力作用下处于平衡状态,现使其中某个力 \(F\) 增大 10 N,为使物体仍处于平衡状态,应采取的措施是( )
A.其他各个力都增大 10 N
B.其他各个力的合力增大 10 N
C.在力\(F\) 的反方向加一个大小为 10 N的力
D.将与\(F\) 反方向的力减小 10 N

第四节
共点力的平衡
二、共点力作用下物体的平衡条件
2

第四节
共点力的平衡
二、共点力作用下物体的平衡条件
正交分解法
物体静止在水平面上
\(T = 10 \rm{N}\)
\(G = 8 \rm{N}\)
\(N = ?\)
\(f_s = ?\)
\(T = 10 \rm{N}\)
\(G = 8 \rm{N}\)
\(N = ?\)
\(f_s = ?\)
\(37\degree\)
\(T_x\)
\(T_y\)

第四节
共点力的平衡
二、共点力作用下物体的平衡条件
正交分解法
物体静止在水平面上
\(T = 10 \rm{N}\)
\(G = 8 \rm{N}\)
\(N = 8 \rm{N}\)
\(f_s = 10 \rm{N}\)
\(G = 8 \rm{N}\)
\(N = ?\)
\(f_s = ?\)
\(T_x = 8 \rm{N}\)
\(T_y = 6 \rm{N}\)

第四节
共点力的平衡
示例

用一根质量可以忽略的细绳悬挂一个空心金属球。当受到电扇吹出的水平风时,细绳将偏离竖直方向一定角度。已知球的重力 \(G\)、偏角 \(\theta\) 。求水平风力 \(F\) 、绳拉力 \(T\) 的大小。
合成法
任两力的合力与第三个力等大反向一直线

第四节
共点力的平衡
示例

用一根质量可以忽略的细绳悬挂一个空心金属球。当受到电扇吹出的水平风时,细绳将偏离竖直方向一定角度。已知球的重力 \(G\)、偏角 \(\theta\) 。求水平风力 \(F\) 、绳拉力 \(T\) 的大小。
正交分解法
建立直角坐标系,沿坐标轴分解力
解方程组得: