Bioestatística e Matemática Aplicada

Prof. Fernando Sales

fernando.sales.ufpe@gmail.com

https://www.ufpe.br/ppgeb/

Sobre o curso

Ementa

Estatística descritiva. Probabilidade. Modelos discretos e contínuos. Ajuste de modelos probabilísticos.
Parâmetros estatísticos. Testes de hipóteses paramétricos, não-paramétricos e para variáveis categóricas.
Correlação e regressão linear. Aplicações de normas de controle de qualidade.

Text

Mais detalhes em: PPGEB UFPE

Bibliografia

CALLEGARI-JACQUES, Sidia M. Bioestatística: princípios e aplicações. Porto Alegre: ARTMED,2004.
VIEIRA, Sônia. Introdução à bioestatística. 3. ed. Rio de Janeiro: Elsevier, 2004.
BERQUÓ, Elza Salvatore; SOUZA, José Maria Pacheco de; GOTLIEB, Sabina Lea Davidson. Bioestatística. 2. ed. Ver. São Paulo: EPU, 2003.
JEKEL, James F.; KATZ, David L.; ELMORE, Joam G. Epidemiologia, bioestatística e medicina
preventiva. Porto Alegre: ARTMED, 2005.
SOARES, José Francisco; SIQUEIRA, Arminda Lucia. Introdução a estatística médica. 2. ed. Belo
Horizonte: COOPMED, 2002.

Outros textos

Estatística: O que é, para que serve, como funciona
por Charles Wheelan
Link: http://a.co/d/5c21rcZ

The Model Thinker: What You Need to Know to Make Data Work for You (English Edition)
por Scott E. Page
Link: http://a.co/d/gvY9mnf

Princípios de bioestatística
por Marcello Pagano
Link: http://a.co/d/7zi7NGy

O que espero...

Photo by Kevin Ku from Pexels

Anyone can...

Photo by Kevin Ku from Pexels

No fundo, será uma PODEROSA "calculadora"...

Photo by Eduardo Rosas from Pexels

E um grande aliado nos processos decisórios...

Photo by rawpixel.com from Pexels

E , confie, é BEM melhor do que fazer "na mão"...

Há inúmeras fontes GRATUITAS disponiveis... e outras pagas!

Recomendo o curso gratuito do módulo "Introduction to R"

Aula 02

13/03/2019

Apresentação tabular e gráfica de dados

Objetivo: Representar os dados em tabelas e gráficos

 

1. Quadro x tabela?

2. O que deve ter numa tabela e num gráfico?

3. Como escolher o melhor tipo de gráfico para o tipo de dados que tenho?

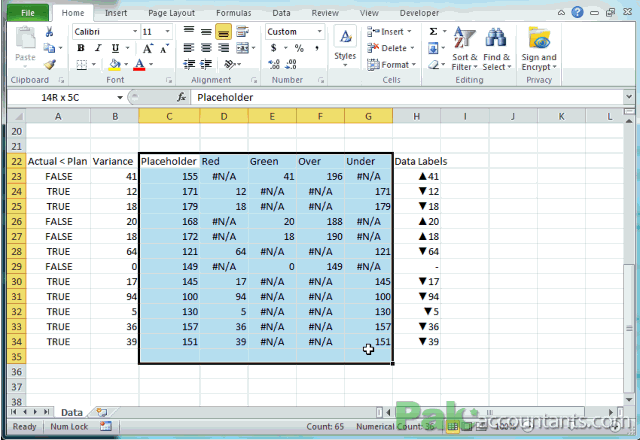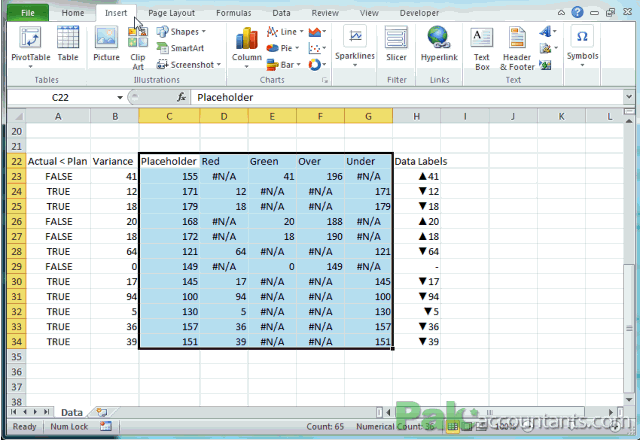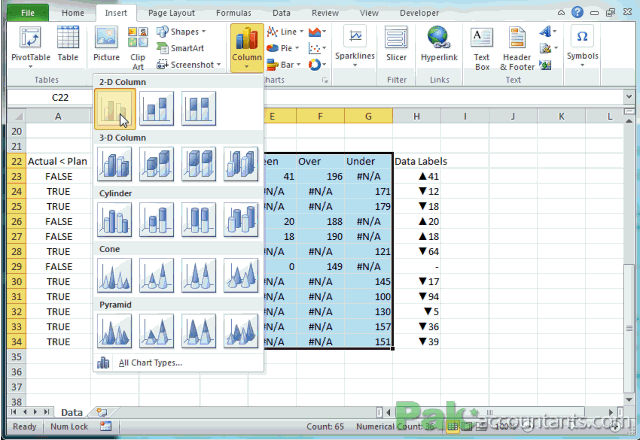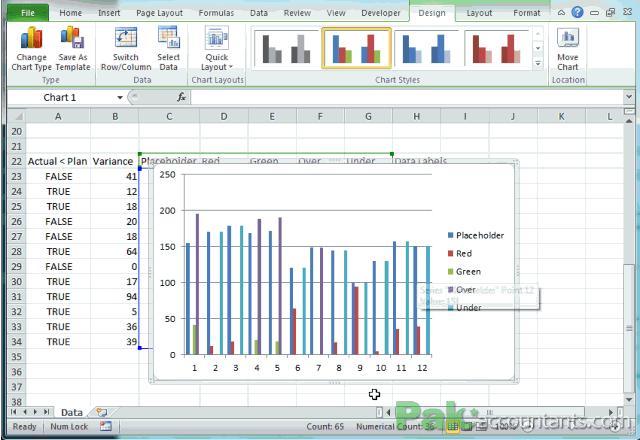
Sobre tabelas, gráficos, figuras, normas... um exemplo!

O que acham desse gráfico? E se quiser mais info?

Quem disse que precisamos ser estáticos?

Yes, WE CAN!

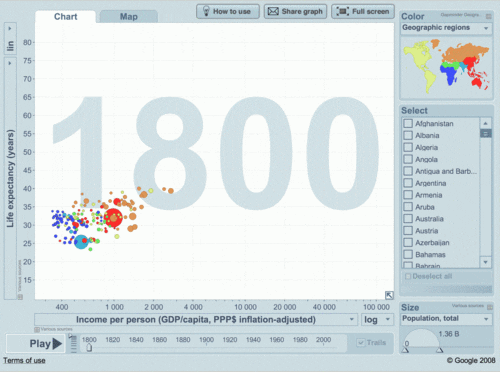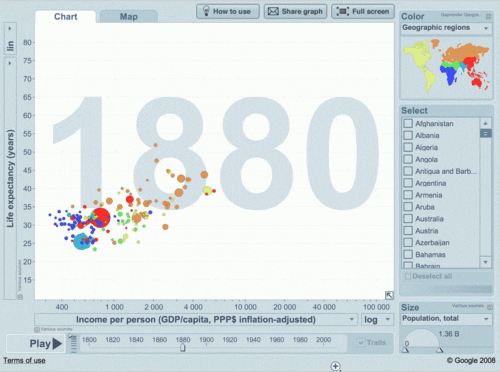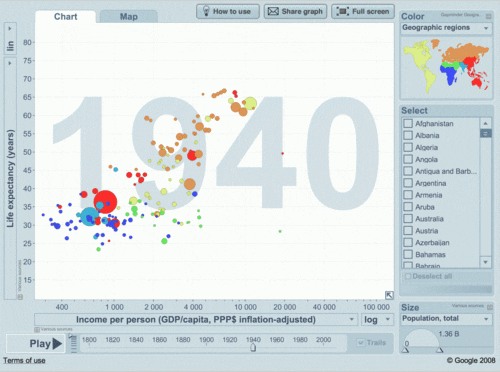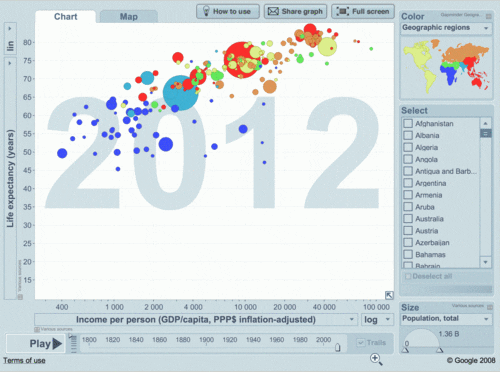
Bem, vamos voltar ao início...

Atividade 1

  1. Carregar o dataset "Pima.tr", disponível no pacote "MASS", distribuído com o R;
  2. Identificar quantas grávidas foram incluídas nesse dataset;
  3. Determinar quais foram os atributos selecionados e os respectivos tipos de variável [numérica, categórica,...]
  4. Façam os seguintes gráficos:
    1. Distribuição da quantidade de gestações por mulher;
    2. Distribuição de idade na amostra;
    3. Relação entre idade e quantidade de gestações
    4. Relação entre o IMC e a glicose
# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 1

5. Faça uma tabela mostrando os seguintes valores de cada atributo na amostra:

  • Min, Max de cada atributo
  • Média, Moda e Mediana
  • Percentil 10, 25, 50, 75 e 90
  • Desvio-Padrão e Distância entre quartis

6. Refaça a tabela fazendo a divisão entre os grupos de diabéticas e não-diabéticas

 

 

 

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 1

7. Suponha que você deseja analisar a distribuição de frequências dos atributos não analisados anteriormente e que tenham valores numéricos. Que tipo de transformação nos dados seria interessante proceder antes de realizar o gráfico? Justifique.

 

8. Refaça os histogramas mudando a largura dos bins. Comente o que muda na distribuição.

 

9. Refaça os histogramas anteriores segregando a amostra em dois grupos de acordo com a presença de diabetes.

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Atividade 2

  1. Refaça todas as tarefas da atividade 1, para os datasets: Pima.tr2 e Pima.te
  2. Faça uma análise comparativa dos resultados obtidos para os valores dos atributos nos diferentes amostras

 

 

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Primeiro, dê uma olhada na variável data na linha de comando

# Procure o comando para visualizar as primeiras linhas
#

Trechos que podem ser úteis

# loading MASS datasets
library(MASS)

# loading PIMA Women diabetes "training" dataset
data = Pima.tr
names(data) = names(Pima.tr)

# Exemplo de cabeçalho
# npreg     glu      bp    skin     bmi     ped     age    type 

# selecting the variables
npreg = data$npreg    # poderia ser npreg = data[,1] -- Seleciona a 1a coluna
glu = data$glu
bp = data$bp
skin = data$skin
bmi = data$bmi
ped = data$ped
age = data$age
type = data$type

# Como selecionar a primeira coluna
data[,1]

# Selecionando a primeira linha
data[1,]

# Selecionando as colunas de dados numéricos - 1 a 7
data[,1:7]

# Selecionando as linhas de pacientes diabéticos e colunas de dados numericos
diab_index = data[,8] == "Yes"
diab = data[diab_index,1:7]

# Selecionando as linhas de pacientes não-diabéticos ["normais"] e colunas de dados numericos
norm_index = data[,8] != "Yes"    # o sinal "!=" equivale a diferente
norm = data[norm_index,1:7]

Sobre o desvio padrão e variância: R Tutorial

# criando um vetor com os máximos [coluna a coluna] 
maximos = apply(data,2,max)

# criando um vetor com os mínimos [coluna a coluna]
minimos = apply(data,2,min)                        # repetir o mesmo para mean, median,...
std = apply(data[,1:7],2,sd)                       # desvio calculado somente pras colunas numéricas [1:7]

# gerando os percentis
percentis = quantile(data$age, c(.10, .25,.50,.75, .90))    # 10, 25, 50, 75 e 90% [10% == 0.1]
distancia = percentis[4] - percentis[2]                     # percentis[4] == 75%; percentis[2] == 25% 

# Gráficos
# 1. Histograma
hist(data$npreg,breaks = 15,xlab = "Number of Pregnancies",
ylab = "Occurencies", main = "Distribution of pregnancies in PIMA.tr database",col = 'blue')

# 2. Scatterplot
plot(data$age,data$npreg,xlab = "Idade (anos)",ylab = "Número de gestações",
main="Relação entre a idade e o número de gestações",col="red")

Mais comandos interessantes: http://mathesaurus.sourceforge.net/octave-r.html  - http://www.cookbook-r.com/

Aula 03

14/03/2019

O que acham disso?

Até mais!

Probabilidade

https://www.khanacademy.org/math/statistics-probability/probability-library/conditional-probability-independence/v/conditional-probability-tree-diagram-example

Uma empresa realiza um exame toxicológico no processo de seleção de seus novos funcionários. O teste específico que eles usam tem uma taxa de falsos positivos de 2% e uma taxa de falsos negativos de 1%. Supondo que 5% dos aplicantes usem drogas ilícitas e um deles seja selecionado aleatoriamente.

 

Dado que o teste seja positivo, qual é a probabilidade dele estar usando drogas?

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

\boxed{p(A|B) = \cfrac{p(A \cap B)}{p(B)}}

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\begin{aligned} &a) \enspace p(Bowl\,1)\, =\, ?\\ &b) \enspace p(vanilla\,|\, Bowl\,1)\, =\, ?\\ &c) \enspace p(chocolate\,|\, Bowl\,2)\, =\, ?\\ &d) \enspace p(vanilla)\, =\, ?\\ &e) \enspace p(chocolate)\, =\, ? \end{aligned}

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & V & C \\ \hline B1 & 30 & 10 \\ \hdashline B2 & 20 & 20 \end{array}}
\boxed{p(\text{Bowl\,1}\,|\,\text{vanilla})\, =\, \cfrac{p(\text{Bowl\,1}\, \cap \text{vanilla})}{p(\text{vanilla})}}

Probabilidade Condicional

Suppose there are two bowls of cookies. Bowl 1contains 30 vanilla cookies and 10 chocolate cookies. Bowl 2 contains 20 of each. Now suppose you choose one of the bowls at random and, without looking, select a cookie at random. The cookie is vanilla. What is the probability that it came from Bowl 1?

Cap. 1, Think Bayes, Allen Downey http://greenteapress.com/wp/think-bayes/

Testes diagnósticos - Definições

  • Sensibilidade (S+) - Probabilidade de um teste dar positivo para uma amostra positiva;

  • Especificidade (S-) - Probabilidade de um teste dar negativo para uma amostra negativa;

  • Acurácia (AC) - Probabilidade de um teste classificar adequadamente uma amostra, isto é, classificar como positiva uma amostra positiva ou como negativa, caso contrário;

  • Taxa de Falsos Negativos (FNR) - Probabilidade de um teste dar negativo para uma amostra positiva;

  • Taxa de Falsos Positivos (FPR) - Probabilidade de um teste dar positivo para uma amostra negativa;

Testes diagnósticos - Definições

  • Valor Preditivo Positivo (PPR) - Probabilidade de uma amostra ser positiva dado o resultado do teste é positivo;

  • Valor Preditivo Negativo (NPR) - Probabilidade de uma amostra ser negativa dado o resultado do teste é negativo;

Testes diagnósticos

\boxed{ \def\arraystretch{1.5} \begin{array}{c:c:c} \, & P & N \\ \hline T^{+}\,[P] & VP & FP \\ T^{-}\,[N] & FN & VN \end{array}}

Padrão-Ouro

Teste

\begin{aligned} \boxed{S^{+}=p(T^{+}|P)=\cfrac{VP}{VP+FN}}& \\ \boxed{S^{-}=p(T^{-}|N)=\cfrac{VN}{VN+FP}}& \\ \boxed{A_{c}=p(T^{+}|P)p(P)+p(T^{-}|N)p(N)}& \\ \boxed{FPR\,=p(T^{+}|N)=\cfrac{FP}{FP+VN}}& \\ \boxed{FNR\,=p(T^{-}|P)=\cfrac{FN}{VP+FN}}& \\ \end{aligned}
\bold{\text{Legenda:} \enspace} \begin{aligned} &P:\, Positivo\\ &N:\, Negativo\\ &T^{+}:\, Teste Positivo\\ &T^{-}:\, Teste Negativo\\ \end{aligned}

Razão de Verossimilhança

  • Definição: razão entre a probabilidades de um evento acontecer em uma população portadora da doença e a probabilidade dele acontecer numa população não portadora;

\begin{aligned} &RV^{+}=\cfrac{p(T^{+}|P)}{p(T^{+}|N)}=\cfrac{S^{+}}{1-S^{-}} \\ &RV^{-}=\cfrac{p(T^{-}|P)}{p(T^{-}|N)}=\cfrac{1-S^{+}}{S^{-}} \\ \end{aligned}

Aplicações - Epidemiologia

  • Incidência - Razão entre a quantidade de novos casos da doença e a quantidade de pessoas expostas;

  • Prevalência - Quantidade de pessoas com a doença [condição] na população;

  • Taxa de Mortalidade - Proporção de pessoas que morreram por uma dada causa na população [em um período de tempo];

  • Letalidade - Proporção de pessoas que morreram por uma dada doença [causa] na população infectada [afetada pela causa];

Aplicações - Epidemiologia

  • Risco Relativo - Razão entre a probabilidade do grupo que tem o fator de risco desenvolver a condição-alvo e a probabilidade do grupo que não tem o fator de risco desenvolver a condição-alvo;

\begin{aligned} &RR=\cfrac{p(P|\text{Exposto})}{p(P|\text{Não\,Exposto})}=\cfrac{I_{E}}{I_{\bar{E}}}=\cfrac{I_{\text{Exposto}}}{I_{\text{Não\,Exposto}}}\\ \end{aligned}

  • Utilidade: Identificação de fatores de risco [RR > 1] ou fatores protetores [RR < 1] em relação a condição em estudo. Muito utilizado na área cardiovascular, sendo muitos resultados obtidos do Framingham Heart Study [70 ANOS!!!]

A famosa COORTE...

Aplicações - Epidemiologia

  • Para determinar esses diversos índices, diferentes desenhos de estudo são possíveis. Caso tenham mais interesse no tema, procurem ler sobre:

    • Estudos Longitudinais

    • Estudos Transversais

    • Estudos de Coorte

    • Estudos Caso - Controle

    • Estudos de Prevalência

  • Sobre os índices da página anterior, reflitam sobre como seriam necessários estudos para inferir os parâmetros definidos lá.

Razão de Chances - Odds Ratio (OR)

  • Nem sempre é possível estimar a incidência de uma dada doença num grupo a partir do desenho do mesmo. Entretanto, é possível fazer uma estimativa em função das chances de uma determinada condição ser desenvolvida nos diferentes grupos da amostra, caso e controle.

\def\arraystretch{1.5} \begin{array}{c:c:c} Grupo & P & N \\ \hline Caso\, & a & b \\ Ctrl\, & c & d \\ \end{array} \\
\begin{aligned} &RV^{+}=\cfrac{p(P|\text{Caso})}{p(P|\text{Ctrl})}=\cfrac{\frac{a}{a+b}}{\frac{c}{c+d}}=\cfrac{a(c+d)}{c(a+b)}\\ &RV^{-}=\cfrac{p(N|\text{Caso})}{p(N|\text{Ctrl})}=\cfrac{\frac{b}{a+b}}{\frac{d}{c+d}}=\cfrac{b(c+d)}{d(a+b)}\\ &OR= \cfrac{RV^{+}}{RV^{-}}=\cfrac{ad}{bc}\\ \end{aligned}

Razão de Chances - Odds Ratio (OR)

  • Nem sempre é possível estimar a incidência de uma dada doença num grupo a partir do desenho do mesmo. Entretanto, é possível fazer uma estimativa em função das chances de uma determinada condição ser desenvolvida nos diferentes grupos da amostra, caso e controle.

\def\arraystretch{1.5} \begin{array}{c:c:c} Grupo & P & N \\ \hline Caso\, & a & b \\ Ctrl\, & c & d \\ \end{array} \\
\begin{aligned} &RV^{+}=\cfrac{p(P|\text{Caso})}{p(P|\text{Ctrl})}=\cfrac{\frac{a}{a+b}}{\frac{c}{c+d}}=\cfrac{a(c+d)}{c(a+b)}\\ &RV^{-}=\cfrac{p(N|\text{Caso})}{p(N|\text{Ctrl})}=\cfrac{\frac{b}{a+b}}{\frac{d}{c+d}}=\cfrac{b(c+d)}{d(a+b)}\\ &OR= \cfrac{RV^{+}}{RV^{-}}=\cfrac{ad}{bc}\\ \end{aligned}

Distribuições de Probabildade

 

Distribuição Binomial (Bernoulli)

Premissas:

  1. Número fixo de ensaios (n), cada um resulta em dois resultados mutuamente exclusivos;
  2. Os resultados dos n ensaios são independentes;
  3. A probabilidade de sucesso (p) para cada ensaio é constante;
P(X=x)=\dbinom{n}{x}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{x}=\cfrac{n!}{x!(n-x)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Distribuição Binomial (Bernoulli)

Exemplo 1: Uma moeda não viciada é utilizada num jogo de cara e coroa "sofisticado" composto por múltiplos lançamentos. Suponha que a moeda seja lançada n vezes em sequência.

a. Seja n = 3. Qual é a probabilidade do número de caras ser igual a zero? Igual a 1? Igual a 2? Igual a 3?

b. Seja n=10. Qual é a probabilidade do número de caras ser igual ao de coroas? E maior? E menor?

c. O que acontece com os casos anteriores se a moeda for trocada por uma moeda cuja probabilidade de cara for igual a 0,7?

P(X=x)=\dbinom{n}{p}p^{x}(1-p)^{n-x},\,\text{onde:\,}\dbinom{n}{p}=\cfrac{n!}{p!(n-p)!}

Observação [Binômio de Newton]

(a+b)^n=\sum\limits_{k=0}^n \dbinom{n}{p}a^{k}\,b^{n-k}
[p+(1-p)]^n=\sum\limits_{k=0}^n \dbinom{n}{p}p^{k}\,(1-p)^{n-k}=\sum\limits_{k=0}^n P(X=k)
\sum\limits_{k=0}^n P(X=k) = (p+1-p)^{n}=1^{n}=1