Flavien Léger

joint works with Pierre-Cyril Aubin-Frankowski,

Gabriele Todeschi, François-Xavier Vialard

Gradient descent with a general cost

What I will present

Main motivation: optimization on a space of measures \(\mathcal{P}(M)\):

minimize   \(E\colon \mathcal{P}(M)\to\mathbb{R}\cup\{+\infty\}\)

Typical scheme:

\mu_{n+1}\in\operatorname*{argmin}_{\mu\in\mathcal{P}(M)} E(\mu)+\frac{1}{2\tau}D(\mu,\mu_n)

where \(D(\mu,\nu)=\)

transport cost:   \(W_2^2(\mu,\nu)\),  \(\mathcal{T}_c(\mu,\nu)\),...

Bregman divergence:   \(\operatorname{KL}(\mu,\nu)\),...

Csiszár divergence:   \(\int_M (\sqrt{\mu}-\sqrt{\nu})^2\),...

Regularized cost

Minimizing movement schemes based on general movement limiters

...

What I will present

Minimizing movement schemes based on general movement limiters

1. Formulations for implicit and explicit schemes with general movement limiter

2. Theory for rates of convergence based on convexity along specific paths, and generalized “\(L\)-smoothness” (“\(L\)-Lipschitz gradients”) for explicit scheme

→ unify gradient / mirror / natural gradient / Riemannian gradient descents

3. Applications

Implicit scheme

D(x,x)=0

Minimize  \(E\colon X\to\mathbb{R}\cup\{+\infty\}\),   where \(X\) is a set (finite  or infinite dimensional...)

Use   \(D\colon X\times X\to[0,+\infty]\)

x_{n+1} \in\operatorname*{argmin}_{x\in X}E(x)+D(x,x_n)

Algorithm

(Implicit scheme)

Motivations for general \(D(x,y)\):

Implicit scheme

  • \(D(x,y)\) tailored to the problem
  • Regularized squared distance
  • Discretizing gradient flows   “\(\dot x(t)=-\nabla E(x(t))\)”

Toy example: \(\dot x(t)=-\nabla^2u(x(t))^{-1}\nabla E(x(t))\), \(u\colon \R^d\to\R\)  strictly convex

Two approaches:

\left\{\begin{aligned} D(x,y)&=\frac{d^2(x,y)}{2\tau},\\ D(x,y)&=\frac{u(x)-u(y)-\langle\nabla u(y),x-y\rangle}{\tau} \end{aligned} \right.

\(d=\) distance for Hessian metric \(\nabla^2 u\)

Explicit minimizing movements: warm-up

\[x_{n+1}=x_n-\frac{1}{L}\nabla E(x_n)\]

\(E\colon \mathbb{R}^d\to\mathbb{R}\)

Gradient descent

“Variational” formulation of Gradient descent:

E

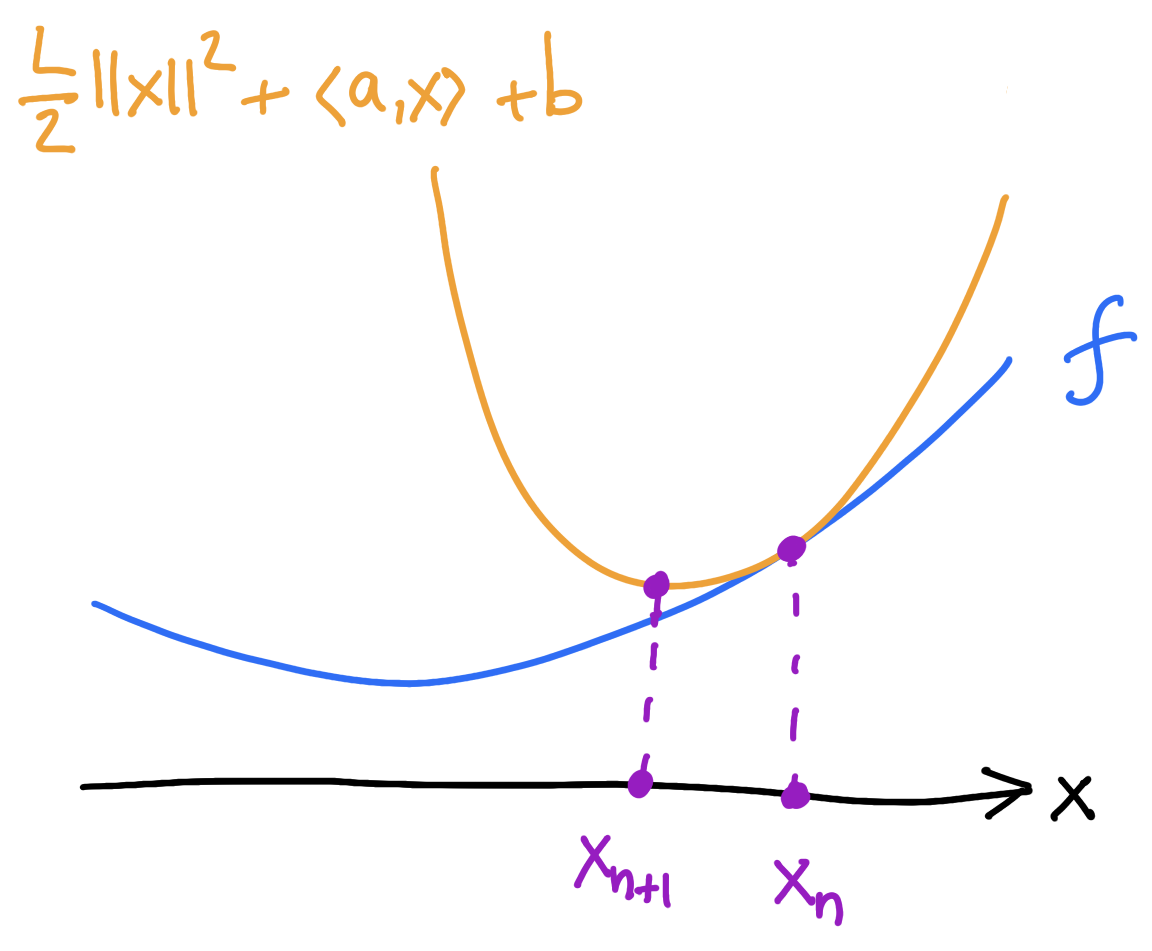
Two steps: 

1) majorize: find the tangent parabola (“surrogate”)

2) minimize: minimize the surrogate

Explicit minimizing movements: warm-up

If \(E\) is \(L\)-smooth (\(\nabla^2 E\preccurlyeq L I_{d\times d}\)) then it sits below the surrogate:

\[E(x)\]

\[\leq\]

\[E(x_n)+\langle\nabla E(x_n),x-x_n\rangle+\frac{L}{2}\lVert x-x_n\rVert^2\]

E

\[x_{n+1}=x_n-\frac{1}{L}\nabla E(x_n)\]

Two steps: 

1) majorize: find the tangent parabola (“surrogate”)

2) minimize: minimize the surrogate

Explicit minimizing movements: c-concavity

E(x)
D\colon X\times Y\to\mathbb{R}\cup\{+\infty\}
E\colon X\to\mathbb{R}\cup\{+\infty\}

\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)

D(x,y)+h(y)
=\inf_{y\in Y}

Definition.

\(E\) is c-concave if

generalizes “\(L\)-smoothness”

Abstract setting:

Smallest such \(h\) is the c-transform

\(h(y)=\sup_{x\in X}E(x)-D(x,y)\)

\(X,Y\): two sets

E(x)

\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)

D(x,y)+h(y)
=\inf_{y\in Y}

Definition.

\(E\) is c-concave if

E
E

c-concave

not c-concave

D(x,y)+h(y)

Explicit minimizing movements: c-concavity

Suppose that \(\forall x\in X,\exists y\in Y\):  \(\nabla_x D(x,y)=\nabla E(x)\) and \(\nabla^2 E (x) \leq \nabla^2_{xx}D(x,y).\)

Then \(E\) is c-concave. 

\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)

Definition.

\(E\) is c-concave if

Explicit minimizing movements: c-concavity

E(x)
D(x,y)+h(y)
=\inf_{y\in Y}

\(E\) is c-concave \(\iff \nabla^2 E\preccurlyeq L\, I_{d\times d}\)

X=Y=\mathbb{R}^d, \quad D(x,y)=\frac{L}{2}\lVert x-y\rVert^2

Example.

Example.

Differentiable NNCC setting.

Explicit minimizing movements

\begin{aligned} y_{n+1}&\in\operatorname*{argmin}_{y\in Y}D(x_n,y)+h(y)\\ x_{n+1} & \in\operatorname*{argmin}_{x\in X}D(x,y_{n+1}) \end{aligned}

(majorize)

(minimize)

E
D\colon X\times Y\to\mathbb{R}\cup\{+\infty\}
E\colon X\to\mathbb{R}\cup\{+\infty\}

Algorithm.

(Explicit scheme)

Assume \(E\) c-concave.

(L–Aubin-Frankowski '23)

D(x,y)+h(y)
\inf_{x\in X}E(x)=\inf_{x\in X,y\in Y}D(x,y)+h(y)

Other point of view:

Explicit minimizing movements

\(X,Y\) smooth manifolds,   \(D\in C^1(X\times Y)\),   \(E\in C^1(X)\) c-concave

\begin{aligned} -\nabla_{\!x} D(x_n,y_{n+1})&=-\nabla E(x_n)\\ \nabla_{\!x} D(x_{n+1},y_{n+1})&=0 \end{aligned}

Under certain assumptions, the explicit scheme can be written as

x_{n+1}-x_n=-\tau\nabla E(x_n)
D(x,y)=\frac{1}{2\tau}\lVert x-y\rVert^2
x_{n+1}=\exp_{x_n}(-\tau\nabla E(x_n))
D(x,y)=\frac{1}{2\tau}d_M^2(x,y)
\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla E(x_n)
D(x,y)=u(x)-u(y)-\nabla u(y)(x-y)
x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla E(x_n)
D(x,y)=u(y)-u(x)-\nabla u(x)(y-x)

2. Convergence rates

EVI and convergence rates

Definition.

\forall x\in X,\quad E(x_n)+D(x_n,y_n)+(1+\mu)D(x,y_{n+1})\leq E(x)+D(x,y_n)

(Csiszár–Tusnády ’84)

(L–Aubin-Frankowski ’23)

Evolution Variational Inequality (or five-point property):

(\mu\geq 0)
x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n), \quad y_{n+1} \in\operatorname*{argmin}_{y\in Y} D(x_n,y)

If \((x_n,y_n)\) satisfy the EVI then

E(x_n)\leq E(x)+\frac{C_0(x,x_0,y_0)}{n}

sublinear rates when \(\mu=0\)

exponential rates when \(\mu>0\)

E(x_n)\leq E(x)+\frac{C_0(x,x_0,y_0,\mu)}{(1+\mu)^n-1}

Theorem.

(L–Aubin-Frankowski '23)

(Ambrosio–Gigli–Savaré ’05)

Variational c-segments and NNCC spaces

⏵  \(s\mapsto (x(s),\bar y)\) is a variational c-segment if \(D(x(s),\bar y)\) is finite and 

⏵  \((X\times Y,D)\) is a space with nonnegative cross-curvature (NNCC space) if variational c-segments always exist.

\(X, Y\) two arbitrary sets,   \(D\colon X\times Y\to\mathbb{R}\cup\{\pm\infty\}\).

(1-s)[D(x(0),\bar y)-D(x(0),y)]+s[D(x(1),\bar y)-D(x(1),y)].
\forall y\in Y\!,\quad D(x(s),\bar y)-D(x(s),y)\leq
x(0)
x(1)
\bar y

Definition.

(L–Todeschi–Vialard '24)

Origins in regularity of optimal transport

(Ma–Trudinger–Wang ’05)

(Trudinger–Wang ’09)

(Kim–McCann ’10)

convexity of the set of c-concave functions

(Figalli–Kim–McCann '11)

Finite dimensional examples

\(D(x,y)=\) Bregman divergence on \(\mathbb{R}^d\)

\(D(x,y)=\lVert x-y\rVert^2\) on \(\mathbb{R}^d\)

Sphere \(\mathbb{S}^d\) with the squared geodesic distance

Bures–Wasserstein

\operatorname{BW}^2(\Sigma_1,\Sigma_2) = \operatorname{tr}(\Sigma_1) + \operatorname{tr}(\Sigma_2) - 2 \operatorname{tr}\left(\sqrt{\Sigma_1^{1/2}\Sigma_2\Sigma_1^{1/2}}\right)

Infinite dimensional examples

Gromov–Wasserstein

Costs on measures. The following are NNCC:

Relative entropy        \(\operatorname{KL}(\mu,\nu)=\int \log\Big(\frac{d\mu}{d\nu}\Big)\,d\mu\),

Hellinger                   \(D(\mu,\nu)=\displaystyle\int\Big(\sqrt{\frac{d\mu}{d\lambda}}-\sqrt{\frac{d\nu}{d\lambda}}\Big)^2\,d\lambda\),

Fisher–Rao = length space associated with Hellinger

Transport costs: squared Wasserstein distance on \(\R^d\), on the sphere...

\((\mathbb{G}\times\mathbb{G},\operatorname{GW}^2)\) is NCCC

\(\mathbf{X}=[X,f,\mu]\)   and   \(\mathbf{Y}=[Y,g,\nu]\in\mathbb{G}\)

\operatorname{GW}^2(\mathbf{X},\mathbf{Y})=\inf_{\pi\in\Pi(\mu,\nu)}\int\lvert f(x,x')-g(y,y')\rvert^2\,d\pi(x,y)\,d\pi(x',y')\,.

G. Peyré

Convergence rates for minimizing movements

Suppose that for each \(x\in X\) and \(n\geq 0\),

Then sublinear (\(\mu=0\)) or linear (\(\mu>0\)) convergence rates. 

⏵ there exists a variational c-segment \(s\mapsto (x(s),y_n)\) on \((X\times Y,D)\) with \(x(0)=x_n\) and \(x(1)=x\)

⏵ \(s\mapsto E(x(s))-\mu \,D(x(s),y_{n+1})\) is convex

⏵ \(\displaystyle\lim_{s\to 0^+}\frac{D(x(s),y_{n+1})}{s}=0\)

Theorem.

(L–Aubin-Frankowski '23)

x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n), \quad y_{n+1} \in\operatorname*{argmin}_{y\in Y} D(x_n,y)
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0)}{n}
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0,\mu)}{(1+\mu)^n-1}

3. Applications

Background on mirror descent

Minimize \(E\colon\R^d\to\R\)   without using the Euclidean structure

Instead use strictly convex \(u\colon\R^d\to\R\).

“Mirror map” \(\nabla u\colon\R^d\to\R^d\) to go from primal to dual space

Mirror descent

\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla E(x_n)

Convergence rates: if \(\mu\nabla^2u\preccurlyeq\nabla^2E\preccurlyeq\nabla^2u\) then

E(x_n)\leq E(x)+\frac{u(x|x_0)}{n}
E(x_n)\leq E(x)+O\Big(\frac{1}{(1+\mu)^n}\Big)
(\mu>0)
(\mu=0)

Nondifferentiable mirror descent

Idea: cost \(D(x,y)=u(x)+u^*(y)-\langle x,y\rangle=u(x|\tilde y)\)      for \(y=\nabla u(\tilde y)\)

\(X=Y=\mathbb{R}^d\), \(u\colon \mathbb{R}^d\to\mathbb{R}\cup\{+\infty\}\) convex

Given \(y_n\),

\left\{\begin{aligned} x_n&\in\partial u^*(y_n)\\ y_n-y_{n+1}&\in\partial E(x_n)\text{ and }y_{n+1}\in\partial(u-E)(x_n) \end{aligned}\right.

\(E\colon \mathbb{R}^d\to\mathbb{R}\cup\{+\infty\}\)

Assume \(E\) convex and \(u-E\) convex

Convergence rate:

E(x_n)\leq E(x)+\frac{D(x,y_0)}{n}

Algorithm.

Theorem.

\(D(x,y)=u(y|x)\longrightarrow\) \(x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla f(x_n)\)

Newton's method: if \(0 \leq \nabla^3f(x)\big((\nabla^2f)^{-1}(x)\nabla f(x),-,-\big) \leq (1-\lambda)\nabla^2f(x)\) then

\[f(x_n)-f_*\leq \Big(\frac{1-\lambda}{2}\Big)^n(f(x_0)-f_*)\]

If \[\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\leq \nabla^2f\leq \nabla^2u+\nabla^3u(\nabla^2u^{-1}\nabla f,-,-)\] then

\[f(x_n)\leq f(x)+\frac{u(x_0|x)}{n}\]

Global rates for Newton's method

Riemannian setting

da Cruz Neto, de Lima, Oliveira ’98

Bento, Ferreira, Melo ’17

2. Explicit:    \(x_{n+1}=\exp_{x_n}\big(-\tau\nabla f(x_n)\big)\)

    \(\operatorname{Riem}\geq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates

    \(\operatorname{Riem}\leq 0\): convexity of \(f\) on c-segments gives \(O(1/n)\) convergence rates

1. Implicit:     \(x_{n+1}=\argmin_{x} f(x)+\frac{1}{2\tau}d_M^2(x,x_n)\)

    \(\operatorname{Riem}\leq 0\): \(\nabla^2f\geq 0\) gives \(O(1/n)\) convergence rates

\(\operatorname{Riem}\geq 0\): convexity of \(f\) on c-segments gives \(O(1/n)\) convergence rates

Thank you!