Fast computations of Wasserstein gradient flows

Joint works with Matt Jacobs and Wonjun Lee (UCLA)

Flavien Léger (Sciences Po, Paris)

$$W_2^2(\mu,\nu) = \inf_{\rho,\phi} \int_0^1\!\!\int |\nabla \phi_t(x)|^2\rho_t(dx)$$

s.t. $ \partial_t\rho+\mathrm{div}(\rho\nabla\phi)=0$,

$\rho_0=\mu, \quad \rho_1=\nu$

Optimal transport

Benamou–Brenier formula

$$W_2^2(\mu,\nu) = \sup_{\phi,\psi} \int_{X} \psi(x)\,\mu(dx) - \int_{Y}\phi(y)\,\nu(dy)$$

s.t. $ \quad \psi(x) - \phi(y) \le |x-y|^2=:c(x,y)$

Optimal transport

$c$-transform:

\begin{aligned} \phi^c(x)&:=\inf_{y\in Y} \, \phi(y)+c(x,y) \\ T_\phi(x)&:=\mathrm{argmin}_{y\in Y} \, \phi(y)+c(x,y) \end{aligned}

\begin{aligned} \psi^c(y)&:=\sup_{x\in X} \, \psi(x)-c(x,y) \end{aligned}

Wasserstein gradient flows

\[\partial_t\rho-\mathrm{div}(\rho\nabla\phi)=0,\]

\[\phi=\delta U(\rho)\]

on a domain $\Omega\subset\mathbb{R}^2$, no flux out and with initial condition $\rho(t=0)=\rho_0$.

Slow diffusion

\[U(\rho)=\int_\Omega \rho(x)^m+V(x)\rho(x)\,dx,\]

$m > 1$. $V(x)$ can be $+\infty$.

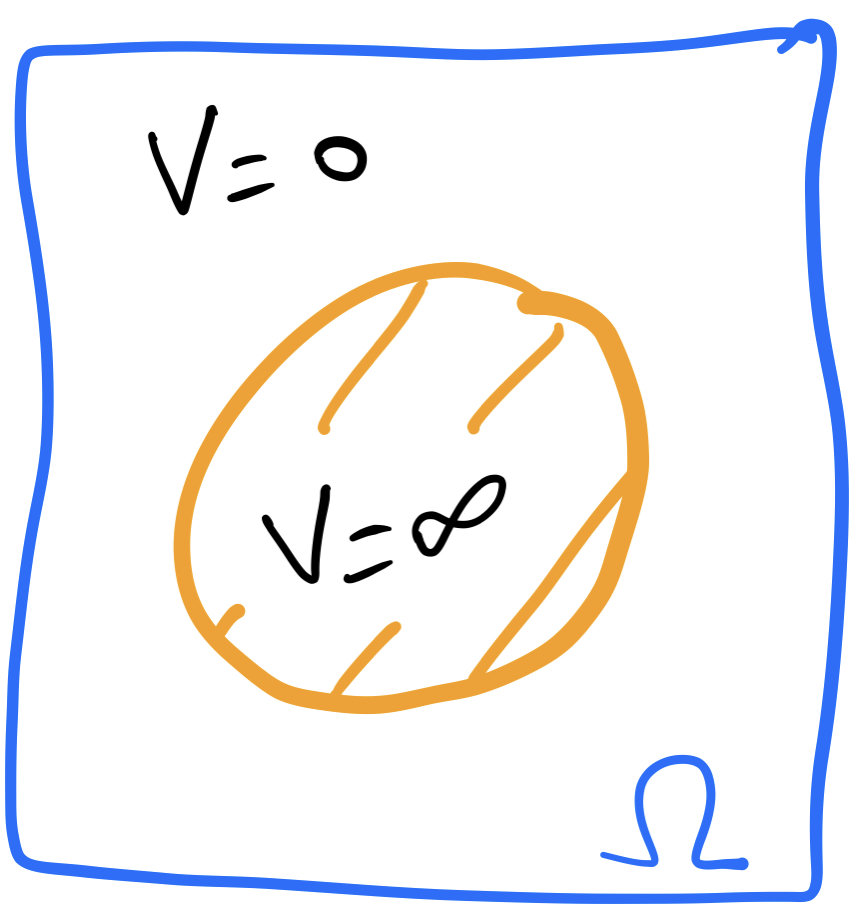
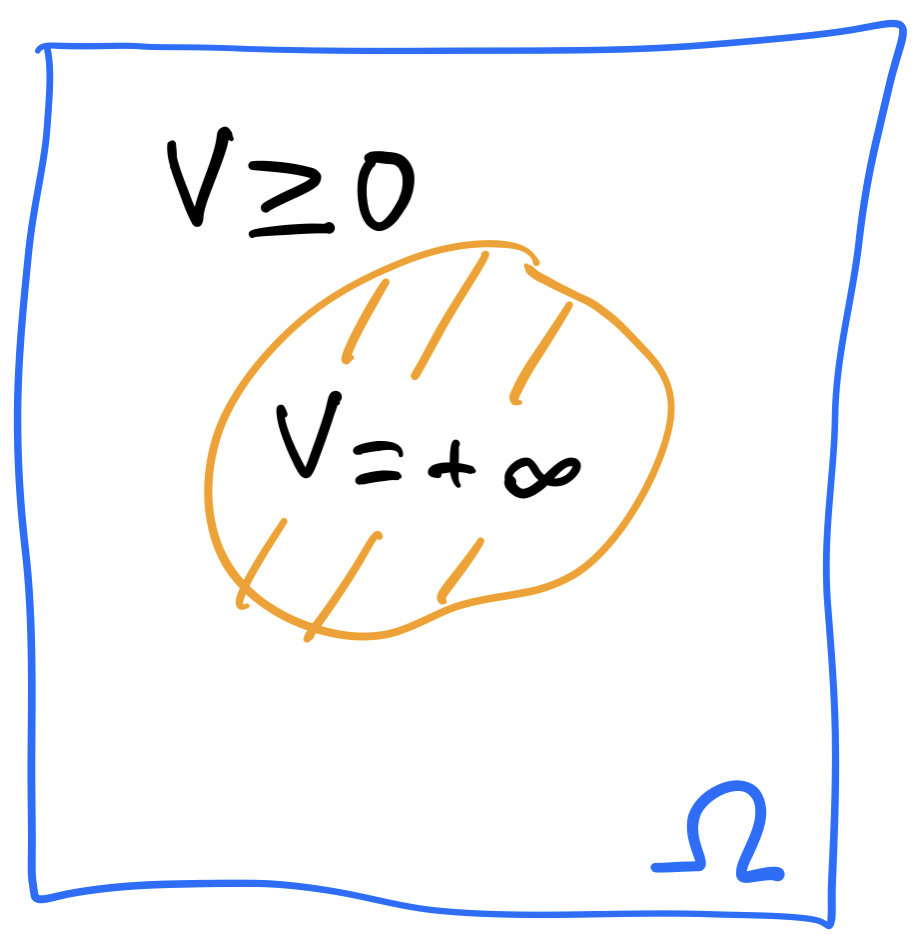
Incompressible energy

\[U(\rho)=\int_\Omega u_\infty(\rho(x))+V(x)\rho(x)\,dx,\]

Aggregation-diffusion

\[U(\rho)=\int_\Omega \rho(x)^m\,dx + \iint_\Omega |x-y|^2\rho(x)\rho(y)\,dxdy\]

u_\infty(\rho)=\begin{cases} 0\quad\text{if } 0\le \rho\le 1\\ +\infty\quad\text{otherwise} \end{cases}

porous medium equation

$\partial_t\rho=\Delta\rho^m$.

JKO scheme

\[\rho^{(n+1)}=\argmin_\rho U(\rho)+\frac{1}{2\tau}W_2^2(\rho^{(n)},\rho)\]

→ need to solve problems of the form

\[\min_\rho \,U(\rho)+\frac{1}{2\tau}W_2^2(\mu,\rho)\]

for a fixed density $\mu$.

$\rho^{(n)} \approx$ solution to the gradient flow at time $t=n\tau$.

$\begin{cases}\partial_t\rho-\mathrm{div}(\rho\nabla\phi)=0 \\ \phi=\delta U(\rho)\end{cases}$ has the variational formulation

Dual formulation

Primal:

Example

$U(\rho)=\iota_{\{\nu\}}(\rho)$ then $U^*(\phi)=\langle\phi,\nu\rangle$.

\[\sup_{\phi,\psi}\,\langle\psi,\mu\rangle - U^*(\phi)\]

over $(\phi,\psi)$ s.t.

\[\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}.\]

\[\inf_\rho U(\rho)+\frac{1}{2\tau}W_2^2(\mu,\rho).\]

Dual:

Dual formulations

Lemma: $U^*$ is increasing, i.e.

\[\phi_1\le\phi_2 \implies U^*(\phi_1)\le U^*(\phi_2).\]

\displaystyle\sup_{\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}}\langle\psi,\mu\rangle - U^*(\phi)

Dual formulations

\displaystyle\sup_{\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}}\langle\psi,\mu\rangle - U^*(\phi)

with $\phi^c(x)=\inf_y\phi(y)+\frac{|x-y|^2}{2\tau}$,

$\psi^c(y)=\sup_x\psi(x)-\frac{|x-y|^2}{2\tau}$.

☇

\[\sup_\phi\langle\phi^c,\mu\rangle-U^*(\phi)=:J(\phi)\]

\[\sup_\psi\langle\psi,\mu\rangle-U^*(\psi^c)=:I(\psi)\]

Dual formulations

→ unconstrained concave maximization problems

→ Recover $\rho^*$ from $\phi^*$ by

\[\rho^*=\delta U^*(\phi^*)\]

\[\sup_\phi\langle\phi^c,\mu\rangle-U^*(\phi)=:J(\phi)\]

\[\sup_\psi\langle\psi,\mu\rangle-U^*(\psi^c)=:I(\psi)\]

The power of duality

\[U(\rho)=\int_\Omega u_\infty(\rho(x))+V(x)\rho(x)\,dx.\]

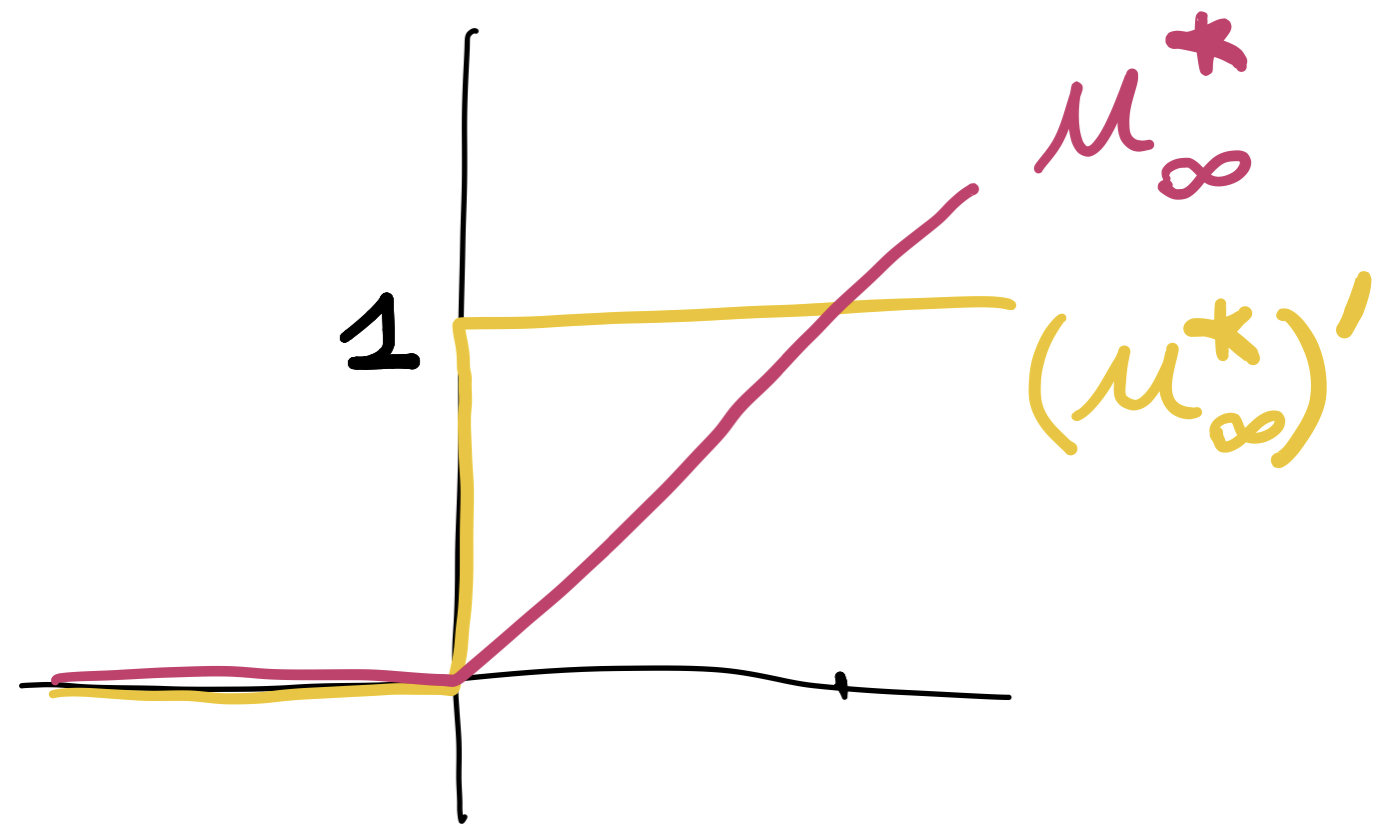
$\rho(x)=(u^*_\infty)'(\phi(x)-V(x))$ guaranteed to be $0$ on obstacle.

Remark

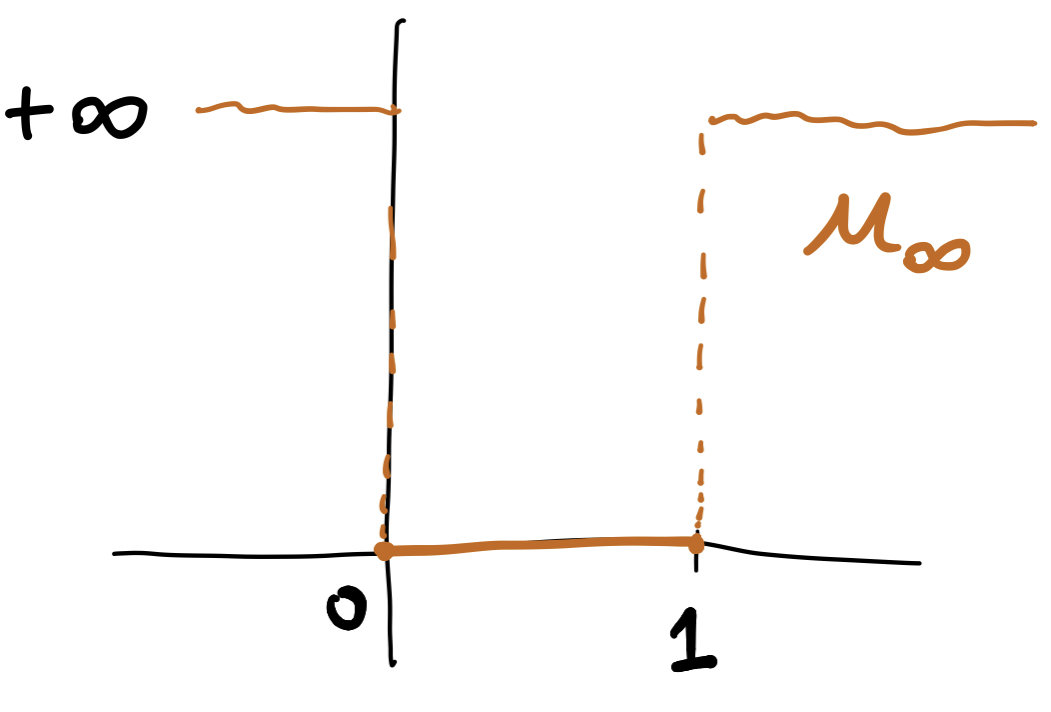
\[U^*(\phi)=\int_\Omega u^*_\infty(\phi(x)-V(x))\,dx\]

☇

Back-and-forth algorithm

$H$ is the Sobolev space

\[\|h\|_H^2=\int_\Omega\Theta_2|\nabla h(x)|^2+\Theta_1|h(x)|^2\,dx\]

\begin{aligned} \phi_{k+\frac 1 2}&=\phi_k+\nabla_{\!H}J(\phi_k),\\ \psi_{k+\frac 1 2}&=(\phi_{k+\frac 1 2})^c,\\ \psi_{k+1}&=\psi_{k+\frac 1 2}+\nabla_{\!H}I(\psi_{k+\frac 1 2}),\\ \phi_{k+1} &= (\psi_{k+1})^c \end{aligned}

$\nabla_{\!H}J(\phi)=(\Theta_1\mathrm{Id}-\Theta_2\Delta)^{-1}\delta J(\phi)$

What is $\nabla_{\!H}J(\phi)$ ?

What is $\delta J(\phi)$ ?

Recall

\begin{aligned} J(\phi)&=\langle\phi^c,\mu\rangle-U^*(\phi)\\ &=:F(\phi)-U^*(\phi) \end{aligned}

Formula:

$$\delta F(\phi)=T_{\phi\#}\mu ,$$

where $T_\phi(x)=\argmin_y\phi(y)+\frac{|x-y|^2}{2\tau}$

Why $H$ ?

Assume that

$$0\le -\delta^2J(\phi)(h,h) \le \lVert h\rVert_H^2$$

for any $\phi,h\in H$. Then the iterations

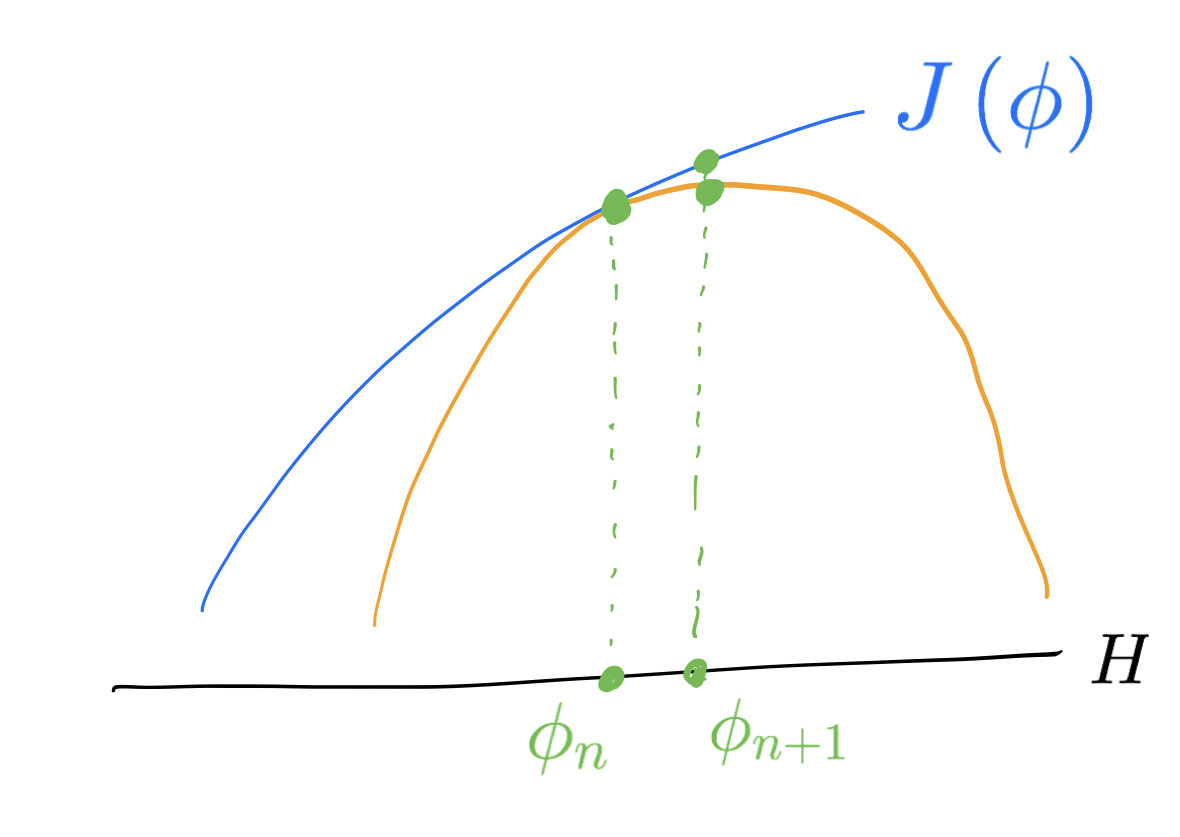
$$\phi_{k+1}=\phi_k+\nabla_{\!H} J(\phi_k)$$

converge to the supremum of $J$.

Fundamental lemma of optimization:

Why $H$ ?

Want Hessian bound

\[0\le -\delta^2\!J(\phi)(h,h)\le \|h\|_H^2\]

$J=F-U^*$ with $F(\phi)=\langle\phi^c,\mu\rangle$

$$ -\delta^2\!F(\phi)(h,h)=\tau\int_\Omega\nabla h(x)\cdot DT_\phi(T_\phi^{-1}(x))\nabla h(x)\,(T_{\phi\#}\mu)(dx) $$

Why $H$ ?

\[U^*(\phi)=\int_\Omega u^*_\infty(\phi(x)-V(x))\,dx\]

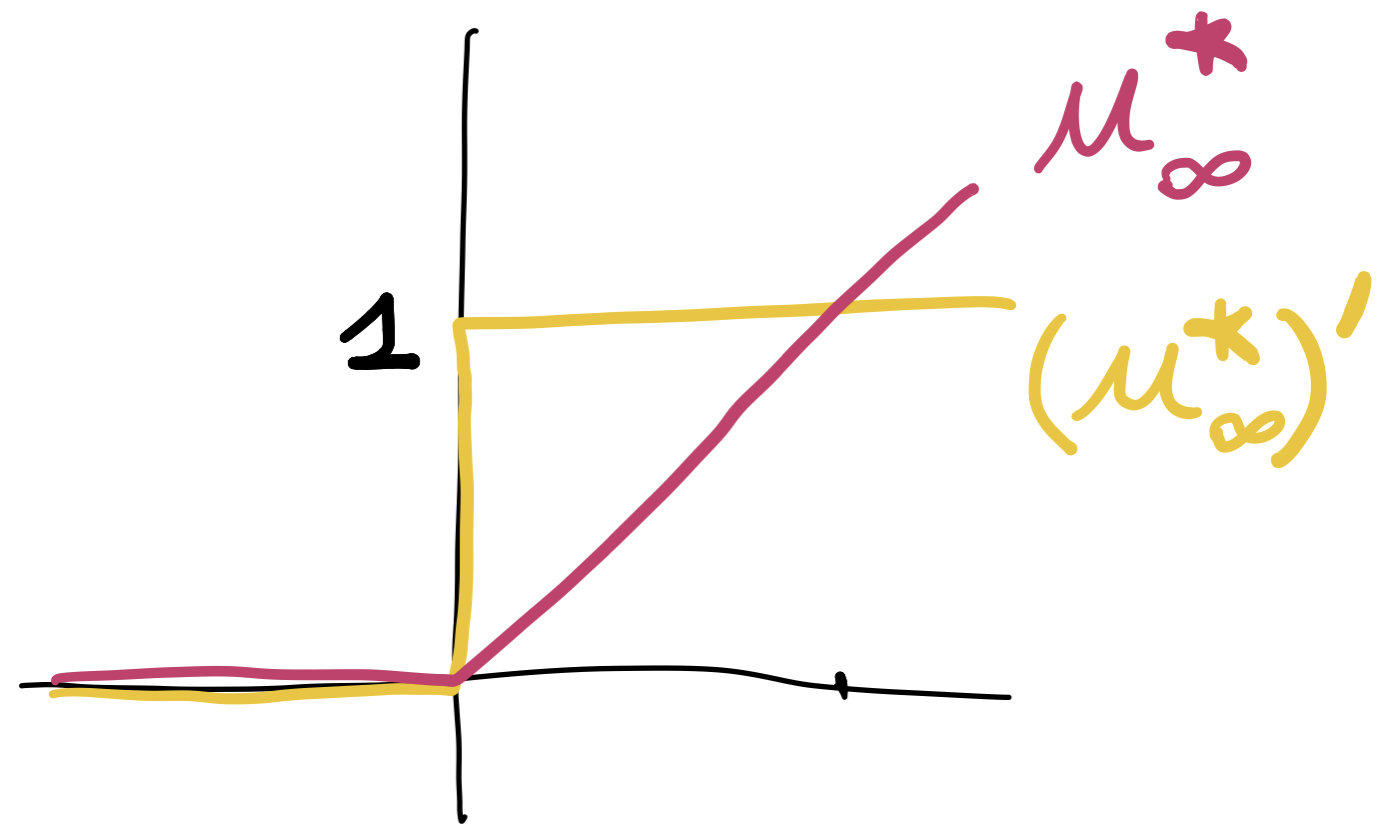
\[\delta^2\!U^*(\phi)(h,h)\le C_\textrm{trace} \int_{\tilde\Omega} |\nabla h(x)|^2+|h(x)|^2\,dx\]

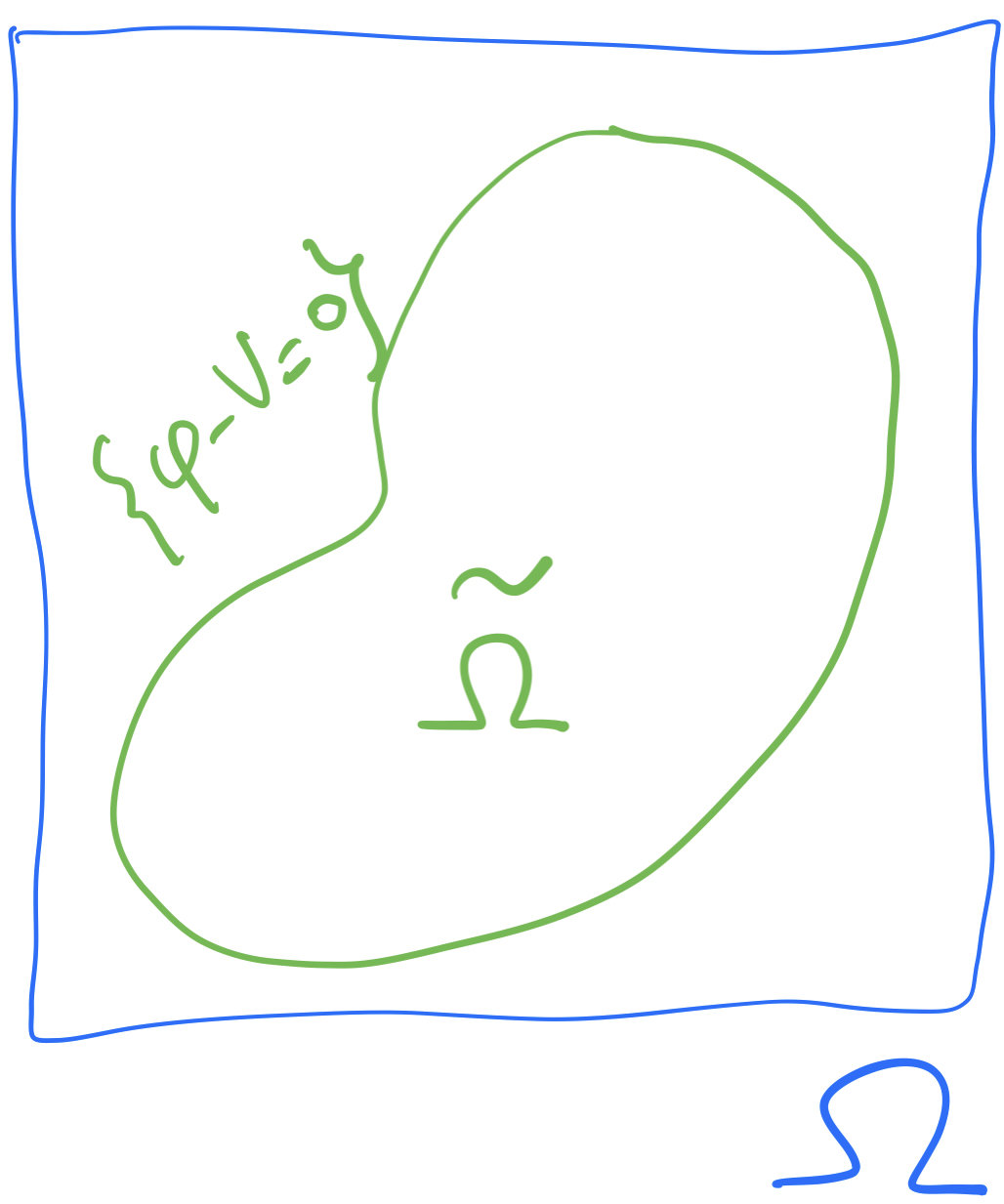
\[\delta^2U^*(\phi)(h,h)=\int_{\{\phi-V=0\}} |h(z)|^2\,d\sigma(z)\]

Back-and-forth is fast

\begin{aligned} \phi_{k+\frac{1}{2}}&=\phi_k+(\Theta_1 - \Theta_2\Delta)^{-1}(T_{\phi_k\#}\mu - \delta U^*(\phi_k)) \\ \psi_{k+\frac{1}{2}}&=(\phi_{k+\frac{1}{2}})^c \end{aligned}

Operations on a grid with $N$ points:

- $c$-transform: $O(N\ln N)$

- $T_{\phi_n} : O(N\ln N) $

- $\Delta^{-1}:O(N\ln N)$