return 5 >>= Lecture

What is a Monad?

Variable — container for data.

Monad — container for computation.

Monad is a general way to describe idea of computations where you can combine computations in a such way so that next computation depends on result of previous computation.

Monad type class

class (Applicative m) => Monad m where  -- m :: * -> *
    return :: a -> m a                  -- return
    (>>=)  :: m a -> (a -> m b) -> m b  -- bind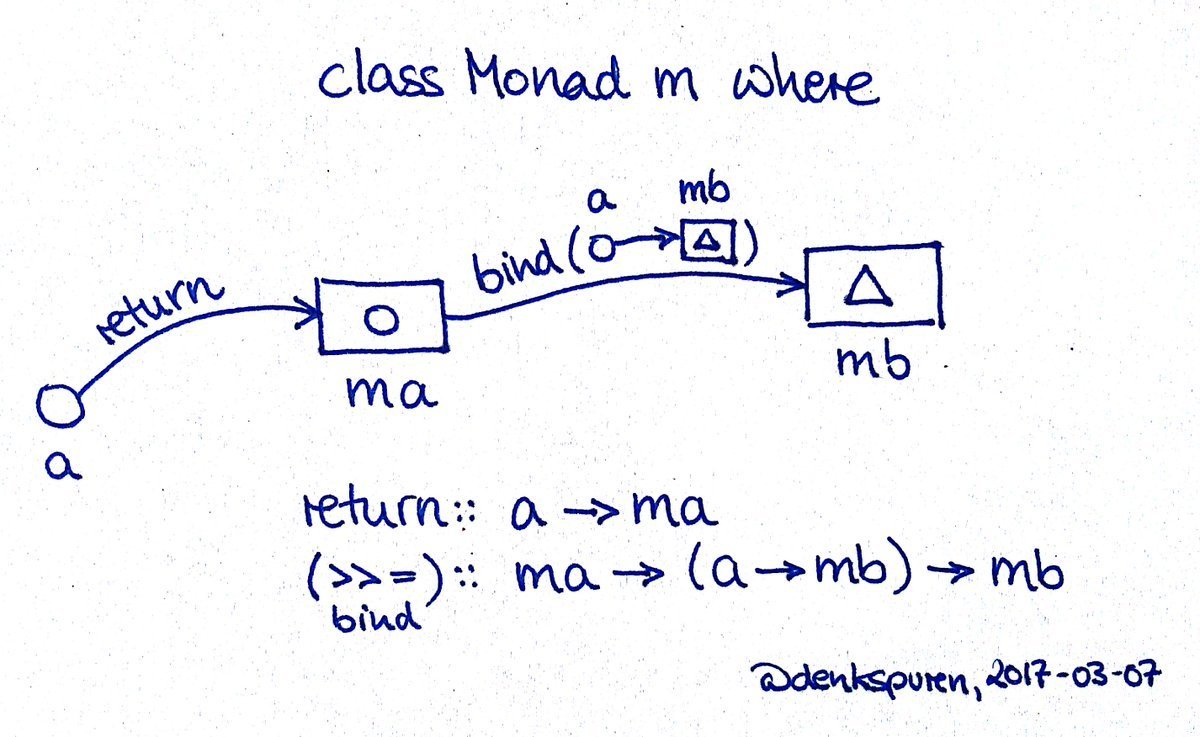

* Image source

Maybe monad

data Maybe a = Nothing | Just a

instance Monad Maybe where
    return :: a -> Maybe a
    return = Just
  
    (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
    Nothing >>= _ = Nothing
    Just a  >>= f = f a

Examples

ghci> Just 5 >>= (\x -> Just $ x + 3)
Just 8

ghci> Just 5 >>= (\x -> return $ x + 3)
Just 8

maybePair :: Maybe a -> Maybe b -> Maybe (a, b)    -- naive implementation
maybePair Nothing  _        = Nothing
maybePair _        Nothing  = Nothing
maybePair (Just a) (Just b) = Just (a, b)

ghci> Nothing >>= (\x -> return $ x + 3)
Nothing

ghci> Just 3 >>= \x -> Just 4 >>= \y -> Just (x + y)
Just 7

maybePair :: Maybe a -> Maybe b -> Maybe (a, b)    -- monadic implementation
maybePair ma mb = ma >>= \a -> mb >>= \b -> Just (a, b)

monadPair :: Monad m => m a -> m b -> m (a, b)    -- polymorphic implementation
monadPair ma mb = ma >>= \a -> mb >>= \b -> return (a, b)

Maybe monad in practice

stripUsername :: String -> Maybe String
stripUsername ""          = Nothing
stripUsername name@(n:ns) = case isSpace n || isPunctuation n of
    True  -> stripUsername ns
    False -> Just name

validateLength :: Int -> String -> Maybe String
validateLength maxLen s = if length s > maxLen
                          then Nothing
                          else Just s

newtype Username = Username String deriving (Eq, Show)

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = ???

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = case stripUsername name of
    Nothing    -> Nothing
    Just name' -> case validateLength 15 name' of
        Nothing     -> Nothing
        Just name'' -> Just $ Username name''

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= validateLength 15 >>= return . Username

YouTube: Teaching Haskell For Understanding by Julie Moronuki

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= \name' ->

                  case validateLength 15 name' of
        Nothing     -> Nothing
        Just name'' -> Just $ Username name''

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= \name' ->

                       validateLength 15 name' >>= \name'' ->

                       Just $ Username name''

Identity monad

newtype Identity a = Identity { runIdentity :: a }

instance Monad Identity where
    return  = Identity
    i >>= f = ...

Either monad

data Either e a = Left e | Right a

instance Monad ...

ghci> :kind Either
Either :: * -> * -> *

instance Monad (Either a) where ...  -- Either a :: * -> *

ghci> :kind Either String
Either String :: * -> *
ghci> :kind Either Int
Either Int :: * -> *

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b
    Left e  >>= f = ...
    Right a >>= f = ...

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b
    Left e  >>= _ = Left e
    Right a >>= f = f a

Types really can help!

Either monad in practice

data ValidationError = InvalidStrip | TooBigLength

stripUsername :: String -> Either ValidationError String
stripUsername ""          = Left InvalidStrip
stripUsername name@(n:ns) = case isSpace n || isPunctuation n of
    True  -> stripUsername ns
    False -> Right name

validateLength :: Int -> String -> Either ValidationError String
validateLength maxLen s = if length s > maxLen
                          then Left TooBigLength
                          else Right s

mkUser :: String -> Either ValidationError Username
mkUser name = stripUsername name >>= validateLength 15 >>= return . Username

ghci> mkUser "   "
Left InvalidStrip
ghci> mkUser " ...  I Am The Greatest Hero Of All Times ... "
Left TooBigLength
ghci> mkUser "JustSenia..."
Right ( Username "JustSenia..." )

Left | Right

ghci> Right True >>= \_ -> Right "foo"
Right "foo" :: Either a [Char]

ghci> Right True >>= \_ -> Left "foo"
Left "foo" :: Either [Char] b

ghci> Left True >>= \_ -> Right "foo"
Left True :: Either Bool [Char]

ghci> Left True >>= \_ -> Left "foo"

    • Couldn't match type ‘[Char]’ with ‘Bool’
      Expected type: Either Bool b
        Actual type: Either [Char] b
    • In the expression: Left "foo"
      In the second argument of ‘(>>=)’, namely ‘\ _ -> Left "foo"’
      In the expression: Left True >>= \ _ -> Left "foo"

You can't mix Left's of different types inside one monadic computation (sequence of >>=). Make sure you understand next code block:

Monad composition

(.)   ::            (b ->   c) -> (a ->   b) -> a ->   c

(<=<) :: Monad m => (b -> m c) -> (a -> m b) -> a -> m c

m >>= (f >=> g) ≡ m >>= f >>= g
m >>= (f <=< g) ≡ m >>= g >>= f

(f >=> g) >=> h ≡ f >=> (g >=> h)    -- associativity

safeTail :: [a] -> Maybe [a]
safeInit :: [a] -> Maybe [a]

safeStrip :: [a] -> Maybe [a]
safeStrip = safeTail >=> safeInit

(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m c

stripUsername  :: String -> Maybe String
validateLength :: Int -> String -> Maybe String

mkUser :: String -> Maybe Username
mkUser name = stripUsername name >>= validateLength 15 >>= Just . Username
mkUser      = stripUsername      >=> validateLength 15 >=> Just . Username

List monad

instance Monad [] where
    return :: a -> [a]
    return x = [x]  -- using bender-operator: return = (:[])
    
    (>>=) :: [a] -> (a -> [b]) -> [b]
    l >>= f  = concat (map f l)  -- or using concatMap

ghci> [10, 5, 7] >>= replicate 3
[10, 10, 10, 5, 5, 5, 7, 7, 7]

surround :: a -> a -> [a] -> [a]
surround '(' ')' "abacaba" = "(a)(b)(a)(c)(a)(b)(a)"

ghci> [1..5] >>= \x -> replicate x x
[1,2,2,3,3,3,4,4,4,4,5,5,5,5,5]

ghci> let step x = [x - 1, x + 1]
ghci> [0] >>= step
[-1,1]
ghci> [0] >>= step >>= step
[-2,0,0,2]
ghci> [0] >>= step >>= step >>= step
[-3,-1,-1,1,-1,1,1,3]
ghci> [0] >>= step >>= step >>= step >>= step
[-4,-2,-2,0,-2,0,0,2,-2,0,0,2,0,2,2,4]

Monad zen

(>>) :: Monad m => m a -> m b -> m b  -- then
m >> k = m >>= \_ -> k

ghci> Just 3 >> Just 5
Just 5

ghci> Nothing >> Just 5
Nothing

Why not?

_ >> k = k

ghci> [True,False] >> [1,2,3]
[1,2,3,1,2,3]

-- 'guard' is a polymorphic function but for lists looks like this:
guard :: Bool -> [()]
guard True  = [()]
guard False = []

ghci> [True,False,True] >> [1,2]
[1,2,1,2,1,2]
ghci> [True,False,True] >>= \b -> guard b >> [1,2]
[1,2,1,2]

Joining monads

join :: Monad m => m (m a) -> m a

ghci> join [[3, 4], [7, 10]]
[3, 4, 7, 10]

ghci> join Just (Just 3)
Just 3

extract :: Monad m => m a -> a    -- ??

ghci> join $ Just [1,2,3]

    • Couldn't match type ‘[]’ with ‘Maybe’
      Expected type: Maybe (Maybe a)
        Actual type: Maybe [a]
    • In the second argument of ‘($)’, namely ‘Just [1, 2, 3]’
      In the expression: join $ Just [1, 2, 3]
      In an equation for ‘it’: it = join $ Just [1, 2, 3]

ghci> join (,) 1          -- niiice
(1,1)

ghci> join replicate 3
[3,3,3]

data Repeat a = Empty | Single a | Repeat a

instance Monad Repeat where
    return :: a -> Repeat a
    return = Single

    (>>=) :: Repeat a -> (a -> Repeat b) -> Repeat b
    Empty    >>= _ = Empty
    Single a >>= f = f a
    Repeat a >>= f = f a >>= f

-- what's the problem with Repeat?

Trying to make a monad

Sometimes simple types can be monads. But in not obvious way.

data Foo a = Bar a | Baz a a

Implementation with laws prove

Functions on monads (1 / 2)

liftM :: Monad m => (a -> b) -> m a -> m b

liftM2 :: Monad m => (a -> b -> c) -> m a -> m b -> m c

ghci> liftM2 (+) (Just 1) (Just 2)
Just 3

Control.Monad

ghci> monadPair (Just 3) (Just 5)
Just (3,5)
ghci> monadPair (Just 3) Nothing
Nothing
ghci> monadPair [1..3] [5,10]
[(1,5), (1,10), (2,5), (2,10), (3,5), (3,10)]

ghci> liftM (+1) (Just 3)
Just 4
ghci> liftM (+1) Nothing
Nothing

ghci> let monadPair = liftM2 (,)
monadPair :: Monad m => m a -> m b -> m (a, b)

Functions on monads (2 / 2)

Control.Monad.Extra

(||^) :: Monad m => m Bool -> m Bool -> m Bool  -- lazy monadic ||
(&&^) :: Monad m => m Bool -> m Bool -> m Bool  -- lazy monadic &&

ghci> Just False ||^ Just True
Just True
ghci> Just False &&^ Just True
Just False
ghci> Just False &&^ Nothing
Just False
ghci> Just True  &&^ Nothing
Nothing
ghci> Nothing    &&^ Just True
Nothing

Going deeper in monad

LearnYouAHaskell (chapter 12)

Yet another monad tutorial (ru)

Monads for functional programming (P. Wadler)

Functors, Applicatives and Monads in pictures

HaskellWikiBook: Understanding Monads/Maybe

Monad laws

1. return a >>= f  ≡ f a                      -- left identity

2. m >>= return    ≡ m                        -- right identity

3. (m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)  -- associativity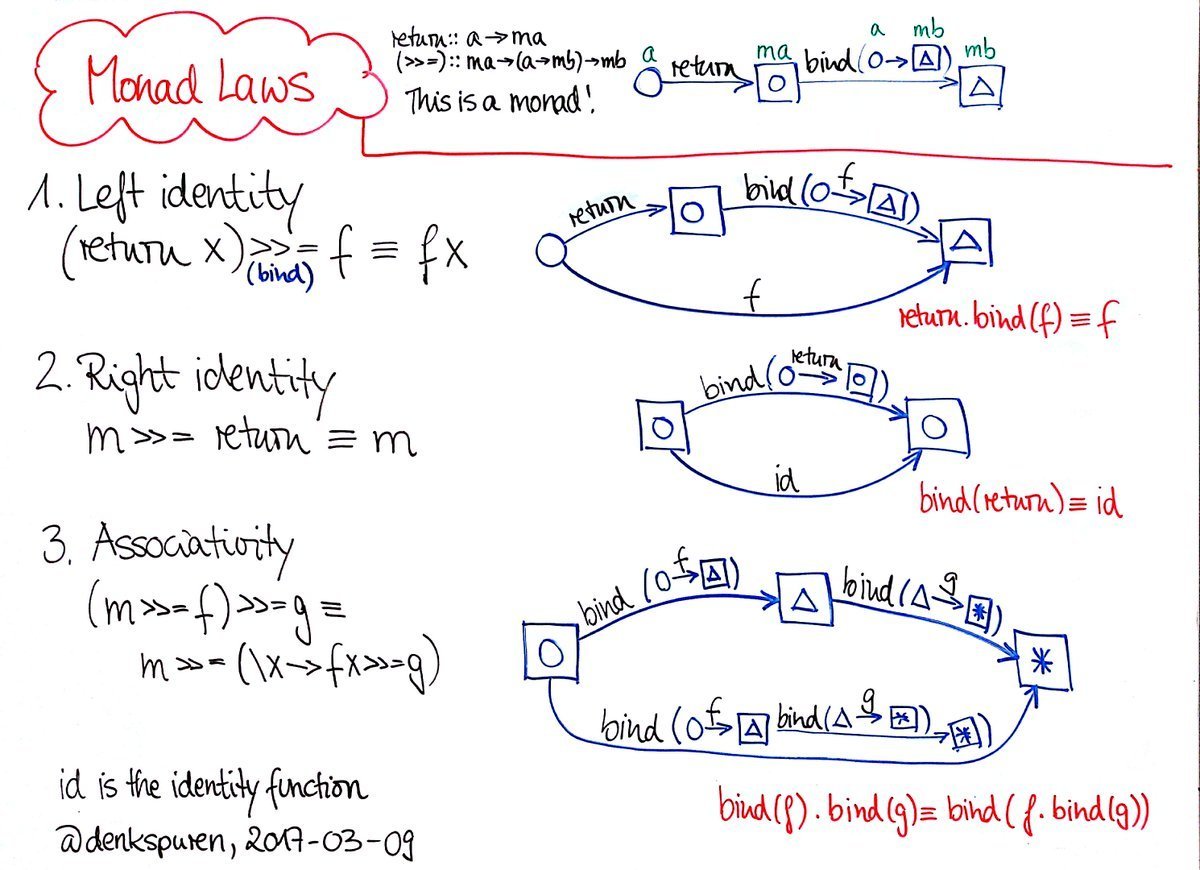

Equational reasoning

To prove one thing equals to another you can use so-called Equational reasoning technique — step-by-step transformation

Lets prove 'foldr (+) 0 [1,2,3] ≡ 6'

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr _ z []     =  z                   -- (1) case
foldr f z (x:xs) =  x `f` foldr f z xs  -- (2) case

foldr (+) 0 [1,2,3] ≡ 1 + foldr (+) 0 [2,3]           -- using (2)
                    ≡ 1 + (2 + foldr (+) 0 [3])       -- using (2)
                    ≡ 1 + (2 + (3 + foldr (+) 0 []))  -- using (2)
                    ≡ 1 + (2 + (3 + 0))               -- using (1)
                    ≡ 1 + (2 + 3)                     -- definition of (+)
                    ≡ 1 + 5                           -- definition of (+)
                    ≡ 6                               -- definition of (+)

So, basically, just sequence of β-redunctions

Proving laws (1 / 2)

instance Monad Maybe where
    return = Just            -- (1): return
  
    Nothing >>= _ = Nothing  -- (2): bind-Nothing
    Just a  >>= f = f a      -- (3): bind-Just

This can be used to prove laws.

Let's prove Monad laws for Maybe

LAW: return a >>= f ≡ f a

LAW: m >>= return ≡ m

return a >>= f ≡ Just a >>= f  -- (1): return
               ≡ f a           -- (3): bind-Just

1. Left Identity

2. Right Identity

Nothing >>= return 
    ≡ Nothing  -- (2): bind-Nothing

Just a >>= return 
    ≡ return a  -- (3): bind-Just
    ≡ Just a    -- (1): return

Proving laws (2 / 2)

instance Monad Maybe where
    return = Just            -- (1): return
  
    Nothing >>= _ = Nothing  -- (2): bind-Nothing
    Just a  >>= f = f a      -- (3): bind-Just

LAW: (m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)

3. Associativity

1. (Nothing >>= f) >>= g
    ≡ Nothing >>= g -- (2): bind-Nothing
    ≡ Nothing       -- (2): bind-Nothing

1. (Just a >>= f) >>= g 
    ≡ f a >>= g  -- (3): bind-Just

2. Nothing >>= (\x -> f x >>= g)
    ≡ Nothing       -- (2): bind-Nothing

2. Just a >>= (\x -> f x >>= g)
    ≡ (\x -> f x >>= g) a  -- (3): bind-Just
    ≡ f a >>= g            -- function application

m ≡ Nothing

m ≡ Just a

List monad nondeterminism 1

powerset :: [a] -> [[a]]  -- all subsets of given list

They will tell you that list monad is about non deterministic evaluation. What does it mean?..

ghci> powerset [1,2,3]
[ [], [ 1 ], [ 2 ], [ 1, 2 ], [ 3 ], [ 1, 3 ], [ 2, 3 ], [ 1, 2, 3 ] ]

-- How to choose nondetermistically subset of list?
subset []       = []
subset (x : xs) = subset xs OR x : subset xs

powerset :: [a] -> [[a]]
powerset []     = [[]]
powerset (x:xs) = powerset xs >>= \set -> [set, x:set]

Replace OR with AND to get all subsets

List monad nondeterminism 2

data CoinType = Fair | Biased deriving (Show)
data Coin     = Head | Tail   deriving (Show, Eq)

Emulate random distribution with list monad

You have two coins, labeled Biased and Fair. The Biased coin has two heads, and the Fair coin has one head and one tail. Pick one of these coins at random, toss it and observe the result. If the result is a head, what is the probability that you picked the Biased coin?

toss :: CoinType -> [Coin]
toss Fair   = [Head, Tail]
toss Biased = [Head, Head]

pick :: [CoinType]
pick = [Fair, Biased]

experiment :: [CoinType]
experiment =
  pick      >>= \coin   ->   -- Pick a coin at random
  toss coin >>= \result ->   -- Toss it, to get a result
  guard (result == Head) >>  -- We only care about results that come up Heads
  return coin                -- Return which coin was used in this case

ghci> experiment
[Biased, Biased, Fair]  -- 2/3 chance for Biased and 1/3 chance for Fair

experiment :: [CoinType]
experiment = [coin | coin <- pick, result <- toss coin, result == Head]