_|_ `seq` Lecture 8

Table of contents

DList

Strictness

Deforestation

Stream Fusion

Mutable Objects

DList

Example: List concatenation

trinity :: [a] -> [a] -> [a] -> [a]
-- which one should we NOT use?
trinity a b c = a ++ b ++ c
trinity a b c = a ++ (b ++ c)
trinity a b c = (a ++ b) ++ c

How to place the parentheses?

Does it even matter?

infixr 5 ++

(++) :: [a] -> [a] -> [a]
[]     ++ b = b
(x:xs) ++ b = x : (xs ++ b)

a =  [1..n] ++ ([1..m]  ++ [1..k]) 
   = [1..n] ++ [1..m, 1..k]      -- m operations
   = [1..n, 1..m, 1..k]          -- n operations
                                 -- m + n total operations
b = ([1..n] ++ [1..m]) ++ [1..k] 
   = [1..n, 1..m] ++ [1..k]      -- n operations
   = [1..n, 1..m, 1..k]          -- n + m operations
                                 -- 2n + m total operations

sum :: [Int] -> Int
sum (x:xs) = x + sum xs
sum []     = 0

Using equational reasoning

Let's pop some bubbles!

(++) :: [a] -> [a] -> [a]
[]     ++ b = b
(x:xs) ++ b = x : (xs ++ b)

a =  [1..n] ++ ([1..m]  ++ [1..k]) 
   = [1..n] ++ [1..m, 1..k]      -- m operations
   = [1..n, 1..m, 1..k]          -- n operations
                                 -- m + n total operations
b = ([1..n] ++ [1..m]) ++ [1..k] 
   = [1..n, 1..m] ++ [1..k]      -- n operations
   = [1..n, 1..m, 1..k]          -- n + m operations
                                 -- 2n + m total operations

Using equational reasoning

Let's pop some bubbles!

Here comes the Difference List

-- import Data.DList
newtype DList a = DL { unDL :: [a] -> [a] }

fromList :: [a] -> DList a
fromList l = DL (l++)

toList :: DList a -> [a] 
toList (DL lf) = lf []

append :: DList a -> DList a -> DList a

(DL f) `append` (DL g) = DL $ \xs -> f (g xs)  -- append = mappend = <>

DL f <> (DL g <> DL h) ≡ DL f <> DL (\xs -> g (h xs)) 
                       ≡ DL f <> DL (\xs -> g' ++ (h' ++ xs))  -- t ≡ (\xs -> ...)
                       ≡ DL f <> DL t
                       ≡ DL $ \ys -> f (t ys) 
                       ≡ DL $ \ys -> f' ++ (t ys)
                       ≡ DL $ \ys -> f' ++ (g' ++ (h' ++ ys))

(DL f <> DL g) <> DL h ≡ DL (\xs -> f (g xs)) <> DL h 
                       ≡ DL (\xs -> f' ++ (g' ++ xs)) <> DL h  -- t ≡ (\xs -> ...)
                       ≡ DL t <> DL h
                       ≡ DL $ \ys -> t (h ys) 
                       ≡ DL $ \ys -> t (h' ++ ys)
                       ≡ DL $ \ys -> f' ++ (g' ++ (h' ++ ys))

Efficient sequences

If you really need efficient sequences:

Seq from Data.Sequence: a finger-tree-based sequence

Strictness

seq

Force evaluation with pattern matching

_|_  -- ⊥, bottom

seq :: a -> b -> b  -- just a model, not a real implementation
_|_ `seq` _ = _|_
_   `seq` b = b

seq evaluates the first argument to its WHNF and returns the second; it does not guarantee the order of evaluation

'Bottom' refers to a computation which never completes successfully (i.e. diverges)

'Bottom' is a member of any type

undefined :: a -- 'bottom', in Haskell

seq quiz

ghci> 0 `seq` 10

ghci> undefined `seq` 10

*** Exception: Prelude.undefined

ghci> Just undefined `seq` 10

10        -- (͡° ͜ʖ ͡°)

data    DataWrapper a    = DW a
newtype NewtypeWrapper a = NW a

ghci> DW undefined `seq` 42
42
ghci> NW undefined `seq` 42
*** Exception: Prelude.undefined

foldr vs. foldl

module Main where

main :: IO ()
main = print $ foldr (+) 0 [1..10^7]

$ ghc --make Main.hs
$ ./Main

10^7: both 'foldr' and 'foldl' are slow

10^8: may crash your system; don't run without a memory limit!

module Main where

import Data.List (foldl')

main :: IO ()
main = print $ foldl' (+) 0 [1..10^7]

10^7: calculates instantly!

10^8: calculates quickly and doesn't crash!

foldr :: (a -> b -> b) -> b -> [a] -> b
foldr _ z []     = z
foldr f z (x:xs) = x `f` foldr f z xs 

foldl :: (b -> a -> b) -> b -> [a] -> b
foldl _ z []     = z
foldl f z (x:xs) = foldl f (z `f` x) xs

sum [1, 2, 3] ≡ foldr (+) 0 [1, 2, 3]
              ≡ 1 + foldr (+) 0 [2, 3]
              ≡ 1 + (2 + foldr (+) 0 [3])
              ≡ 1 + (2 + (3 + foldr (+) 0 []))
              ≡ 1 + (2 + (3 + 0))
              ≡ 1 + (2 + 3)
              ≡ 1 + 5
              ≡ 6

sum [1, 2, 3] ≡ foldl (+) 0 [1, 2, 3]
              ≡ foldl (+) (0 + 1) [2, 3]
              ≡ foldl (+) ((0 + 1) + 2) [3]
              ≡ foldl (+) (((0 + 1) + 2) + 3) []
              ≡ ((0 + 1) + 2) + 3
              ≡ (1 + 2) + 3
              ≡ 3 + 3
              ≡ 6

> foldr (&&) False (repeat False)

ER on foldr and foldl

> foldl (&&) False (repeat False)

False

*hangs*

sum [1, 2, 3] ≡ foldl' (+) 0 [1, 2, 3]
              ≡ foldl' (+) 1 [2, 3]
              ≡ foldl' (+) 3 [3]
              ≡ foldl' (+) 6 []
              ≡ 6

What does foldl' do?

foldl' :: (a -> b -> a) -> a -> [b] -> a
foldl' f a []     = a
foldl' f a (x:xs) = let a' = f a x
                    in seq a' (foldl' f a' xs)

How seq helps

f (acc, len) x = (acc + x, len + 1)

foldl' f (0, 0) [1, 2, 3]
 = foldl' f (0 + 1, 0 + 1) [2, 3]
 = foldl' f ((0 + 1) + 2, (0 + 1) + 1) [3]
 = foldl' f (((0 + 1) + 2) + 3, ((0 + 1) + 1) + 1) []
 = (((0 + 1) + 2) + 3, ((0 + 1) + 1) + 1)

seq doesn't quite help in certain situations...

deepseq

ghci> import Control.DeepSeq
ghci> [1, 2, undefined] `seq` 3
3
ghci> [1, 2, undefined] `deepseq` 3
*** Exception: Prelude.undefined

-- ??
ghci> repeat False `seq`     15 
ghci> repeat False `deepseq` 15

NFData

class NFData a where  -- Normal Form Data
    rnf :: a -> ()
    rnf a = a `seq` ()

The 'Once' trick to avoid excessive rnf calls

instance NFData a => NFData (Maybe a) where
    rnf Nothing  = ()
    rnf (Just x) = rnf x

instance NFData a => NFData [a] where
    rnf []     = ()
    rnf (x:xs) = rnf x `seq` rnf xs

deepseq :: NFData a => a -> b -> b
a `deepseq` b = rnf a `seq` b

Why do we need a typeclass for deepseq?

sum

sum :: Num a => [a] -> a
sum []     = 0
sum (x:xs) = x + sum xs

What's wrong with all these implementations?

newtype Sum a = Sum { getSum :: a }

instance Num a => Monoid (Sum a) where
    mempty = Sum 0
    Sum x `mappend` Sum y = Sum (x + y)

sum :: Num a => [a] -> a
sum = getSum . foldMap Sum

sum :: Num a => [a] -> a
sum = go 0
  where
    go acc (x:xs) = go (acc + x) xs
    go acc []     = acc

III

sum [1,2,3] ≡ 1 + sum [2,3] 
            ≡ 1 + (2 + sum [3])
            ≡ 1 + (2 + (3 + sum []))
            ≡ 1 + (2 + (3 + 0))
            ≡ 1 + (2 + 3)
            ≡ 1 + 5
            ≡ 6

-XBangPatterns

sum :: Num a => [a] -> a
sum = go 0
  where
    go acc (x:xs) = go (acc + x) xs  -- the 'acc' pattern is too lazy
    go acc []     = acc

{-# LANGUAGE BangPatterns #-}

sum :: Num a => [a] -> a
sum = go 0
  where
    go !acc (x:xs) = go (acc + x) xs
    go  acc []     = acc

sum :: Num a => [a] -> a
sum = go 0
  where
    go acc _ | acc `seq` False = undefined  -- that's why we need `seq`
    go acc (x:xs)              = go (acc + x) xs
    go acc []                  = acc

Can be understood in the following way:

More bang patterns

stackOps :: State Stack Int  -- type Stack = [Int]
stackOps = do 
    !x <- pop
    push 42
    return x

($!) :: (a -> b) -> a -> b                 -- a strict function application
f $! x = let !vx = x in f vx

($!!) :: NFData a => (a -> b) -> a -> b  -- the strictest function application
f $!! x = x `deepseq` f x

randomSum :: Int -> IO Int
randomSum n = do 
    randList <- replicateM n $ randomRIO (0, 10)
    return $! sum randList

f1 !(x,y) = [x,y]
f2 (x,y)  = [x,y]  -- how do f1 and f2 differ?

g (!x, y) = [x,y]

let (!x,[y]) = e in b

Lazy pattern matches

f :: (a, b) -> Int
f  (a, b) = const 1 a -- this pair pattern is too strict

g :: (a, b) -> Int
g ~(a, b) = const 1 a -- lazy/irrefutable pattern match

ghci> f undefined
*** Exception: Prelude.undefined

ghci> g undefined
1

lazyHead :: [a] -> a
lazyHead ~[]    = undefined
lazyHead ~(x:_) = x

f1 :: Either e Int -> Int
f1 ~(Right 1) = 42

ghci > f1 (Left "the hehes")
42
ghci > f1 (error "and the hahas")
42

Strict Haskell

data Config = Config
    { users ::  Int
    , extra ::  Maybe Settings
    } deriving Show

data Config = Config  -- with strict fields
    { users :: !Int
    , extra :: !(Maybe Settings)  
    } deriving Show

data Config = Config
    { users :: Int
    , extra :: Maybe Settings  
    } deriving Show

{-# LANGUAGE StrictData #-}

Also since GHC 8

{-# LANGUAGE Strict #-}  -- but it's used ultra-rarely

Makes everything strict by default

Strict fields help avoid space leaks

Using them can decrease memory consumption of the program

Roman Cheplyaka: How much space does an 8-bit integer occupy in C and Haskell?

When to use strict evaluation?

1. When your program runs slow or crashes with StackOverflow: strict evaluation could help.

2. Arithmetic operations (+, *, square, etc.) / numeric computations

3. Reduce the growth of calling functions (or in the case of recursion):

f x = g $! (h x)

f x = g x -- no strict application, all is ok

f !x = g (h x) -- f is strict by argument, no need to call $!

not a necessary rule but it could be helpful

4. Fields of data types (to avoid space leaks)

Did someone say space leaks?

bad :: [Double] -> (Double, Int)
bad xs = (Prelude.sum xs, Prelude.length xs)  -- an unavoidable space leak here

import qualified Control.Foldl as L

good :: [Double] -> (Double, Int)
good xs = L.fold ((,) <$> L.sum <*> L.length) xs

Using Gabriella Gonzalez's foldl library

ghci> let average = (/) <$> L.sum <*> L.length
ghci> L.fold average [1..10]
5.5

And it becomes even better

Video presentation by Gabriella

import Data.List (foldl')

bad2 :: Num a => [a] -> (a, Int)
bad2 xs = foldl' step (0, 0) xs
  where
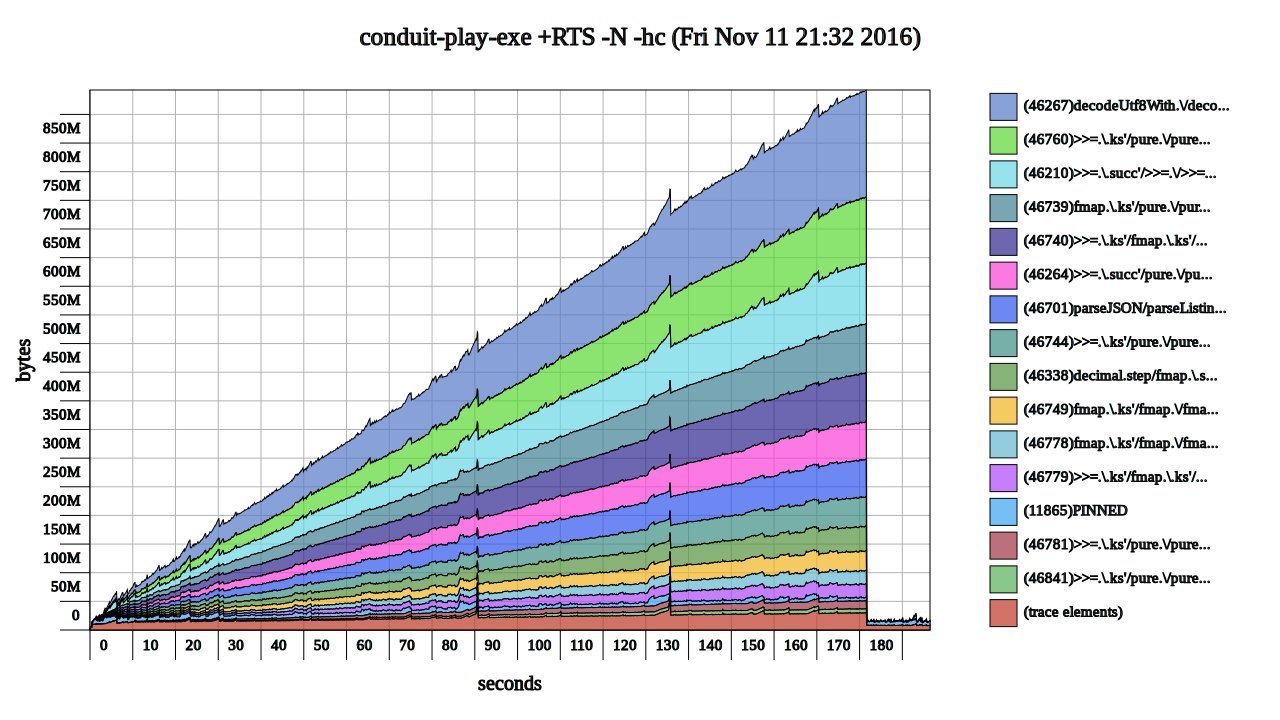
    step (x, y) n = (x + n, y + 1)

Scary pictures

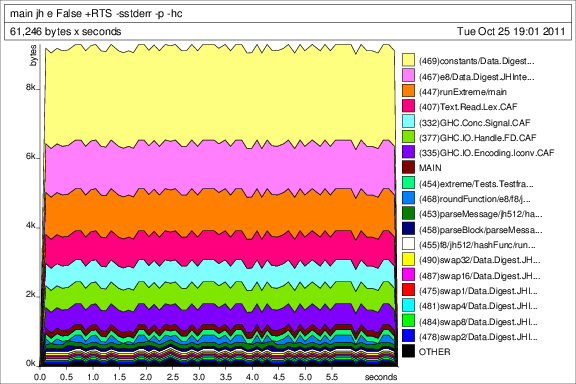
Normal work

Typical space leak

Detecting space leaks

Deforestation

Examples

map f     . map g = map (f . g)     -- we want one traversal
sum        (map (^2) [1 .. n])      -- essentially a loop w/ an intermediate list 
filter p  . map f = ??              -- should work for infinite lists
foldr f z . map g = foldr (f . g) z -- «Fusion Property»

map :: (a -> b) -> [a] -> [b]
map _ []     = []
map f (x:xs) = f x : map f xs

-- equivalent form
map :: (a -> b) -> [a] -> [b]
map f l = case l of
               []     -> []
               (x:xs) -> f x : map f xs

Let's desugar 'map' to prepare for deforestation

Deforestation example

func = foldr (+) 0 . map (\x -> x * 10)  -- original function

-- step 0: unfold the definition of composition w/ eta-expansion
func l = foldr (+) 0 (map (\x -> x * 10) l)

-- step 1: inline the body of foldr
func l = case (map (\x -> x * 10) l) of []     -> 0
                                        (x:xs) -> x + (foldr (+) 0 xs)

-- step 2: inline the body of map, unfold the lambda
func l = case (case l of []     -> []
                         (y:ys) -> y * 10 : map (\x -> x * 10) ys) of
              []     -> 0
              (x:xs) -> x + (foldr (+) 0 xs)

-- step 3: apply the case-of-case transformation
func l = case l of []     -> (case [] of []     -> 0
                                         (x:xs) -> x + (foldr (+) 0 xs))
                   (y:ys) -> (case (y * 10 : map (\x -> x * 10) ys) of
                                   []     -> 0
                                   (x:xs) -> x + (foldr (+) 0 xs))

-- step 4: unfold the inner cases by analyzing the constructors
func l = case l of []     -> 0
                   (y:ys) -> y * 10 + (foldr (+) 0 (map (\x -> x * 10) ys))

-- step 5: replace the last call with the recursive call
func l = case l of []     -> 0
                   (y:ys) -> y * 10 + func ys

Stream Fusion

From Lists to Streams

newtype List a = List ([a] -> Maybe (a, [a]))

I. Naive streams

Let's implement map1

map1 :: (a -> b) -> List a -> List b
map1 g (List f) = List h
  where
    h s' = case f s' of
      Nothing       -> Nothing
      Just (x, s'') -> Just (g x, s'')

But it doesn't type check

Couldn't match type a with b

g x :: b
s'' :: [a]

g x :: b
s'' :: [a]

From Lists to Streams

newtype List a b = List ([a] -> Maybe (b, [a]))  -- typechecks, but ugly

II. Less naive streams

data List a b = List ([a] -> Maybe (b, [a])) [a]  -- the penultimate version

III. List streams

data Step s a = Done 
              | Skip    s 
              | Yield a s

data Stream a = forall s . Stream (s -> Step s a) s

IV. Stream fusion

Stream Fusion

stream :: forall a . [a] -> Stream a
stream xs = Stream next xs 
  where
    next :: [a] -> Step [a] a
    next []     = Done
    next (x:xs) = Yield x xs

data Step s a = Done 
              | Skip    s 
              | Yield a s

data Stream a = forall s . Stream (s -> Step s a) s
                                     ││           │
                                     ││           └── the stream itself
                                     ││
                                     └┴── the stream extractor

unstream :: forall a . Stream a -> [a]
unstream (Stream next s0) = go s0 
  where
    go s = case next s of 
             Done       -> []
             Skip s'    -> go s'
             Yield a s' -> a : go s'

mapS :: forall a b . (a -> b) -> Stream a -> Stream b
mapS f (Stream next s) = Stream next' s 
  where
    next' xs = case next xs of 
                    Done       -> Done
                    Skip s'    -> Skip s'
                    Yield a s' -> Yield (f a) s'

filterS :: forall a . (a -> Bool) -> Stream a -> Stream a
filterS p (Stream next s) = Stream next' s 
  where
    next' xs = case next xs of 
                    Done       -> Done
                    Skip s'    -> Skip s'
                    Yield a s' -> if p a then Yield a s' else Skip s'

Simple stream fusion functions

foldrS left as an exercise

An example of fast numerical computation using Haskell

map :: (a -> b) -> [a] -> [b]
map f = unstream . mapS f . stream

Stream fusion optimization

filter :: (a -> Bool) -> [a] -> [a]
filter p = unstream . filterS p . stream

foo ≡            map  show          .            filter  even

    ≡            map  show          . unstream . filterS even . stream

    ≡ unstream . mapS show . stream . unstream . filterS even . stream
                               │          │
                               └────┬─────┘
                                    │
                         nuked by a rewrite rule

{-# RULES "stream/unstream" 
    forall (s :: Stream a) . stream (unstream s) = s 
  #-}

What on earth is a rewrite rule?

Hackage: stream-fusion — stream fusion for lists

Github: bytestring — stream fusion for ByteString

Sequences: Stream fusion ≫= Rewrite Rules ≫= Deforestation

Mutable Objects

import Data.Array.IO

arrayOps :: IO Int
arrayOps = do 
    arr <- newArray (0, 100) 42 :: IO (IOArray Int Int)
    a   <- readArray arr 1
    writeArray arr 2 (64 + a)
    readArray arr 2

What is the problem with an IO array?

-- import Control.Monad.ST
data ST s a  -- The strict ST monad providing support for strict state "threads"

Pure mutable objects

runState :: State s a -> s -> (a, s)  -- use evalState to get the result
runST    :: (forall s. ST s a) -> a   -- the forall trick

data STRef s a  -- a mutable variable

newSTRef    :: a -> ST s (STRef s a) 
readSTRef   :: STRef s a -> ST s a
writeSTRef  :: STRef s a -> a -> ST s ()
modifySTRef :: STRef s a -> (a -> a) -> ST s ()

import Control.Monad.ST
import Data.STRef
import Data.Foldable

sumST :: Num a => [a] -> a
sumST xs = runST $ do
    n <- newSTRef 0
    for_ xs $ \x ->
        modifySTRef n (+x)
    readSTRef n

Imperative Haskell: Haskell quicksort on mutable arrays

-- import Data.Array.ST
data STArray s i e :: * -> * -> * -> *  -- Mutable, boxed, non-strict arrays
-- s: the state variable argument for the ST type
-- i: the index type of the array (should be an instance of Ix), usually Int
-- e: the element type of the array

Mutable arrays

newArray   :: Ix i => (i, i) -> e -> m (a i e)
readArray  :: (MArray a e m, Ix i) => a i e -> i -> m e
writeArray :: (MArray a e m, Ix i) => a i e -> i -> e -> m ()

class Monad m => MArray a e m where  -- type class for all arrays

data STUArray s i e  -- A mutable array with unboxed elements 
                     -- (Int, Double, Bool, etc.)
                     -- Has support of a very exclusive set of the element types!

Mutable dynamic arrays

data Vector    a  -- immutable vectors
data MVector s a  -- mutable vectors

-- immutable vectors
(!) :: Vector a -> Int -> a  -- O(1) indexing
fromList :: [a] -> Vector a
map, filter, etc.

-- mutable vectors
read   :: (PrimMonad m, MVector v a) => v (PrimState m) a -> Int -> m a
write  :: (PrimMonad m, MVector v a) => v (PrimState m) a -> Int -> a -> m ()
grow   :: PrimMonad m => MVector (PrimState m) a -> Int 
                      -> m (MVector (PrimState m) a)
freeze :: PrimMonad m => MVector (PrimState m) a -> m (Vector a)
-- holy types O_O

Compare immutable and mutable implementations

module ListInsertionSort where

-- span (> 3) [4,5,4,1,4,7] == ([4,5,4],[1,4,7])
sort :: [Int] -> [Int]  -- list sort
sort = insS []
  where
    insS sl []     = sl
    insS sl (x:xs) = let (lower, greater) = span (< x) sl
                     in insS (lower ++ (x : greater)) xs

STUArray implementation

module ArrayInsertionSort where

import Control.Monad.ST
import Data.Array.ST
import Data.Foldable (forM_)
import Control.Monad (unless)

type IntArray s = STUArray s Int Int

sort :: [Int] -> [Int]  -- sort on mutable arrays
sort list = runST $ do
    let listSize = length list
    arr <- newListArray (0, listSize - 1) list :: ST s (IntArray s)

    forM_ [1..listSize - 1] $ \i ->
        forM_ [i-1, i-2..0] $ \j -> do
            cur  <- readArray arr j
            next <- readArray arr (j + 1)
            unless (cur <= next) $ do writeArray arr j next
                                      writeArray arr (j + 1) cur

    getElems arr

MVector implementation

{-# LANGUAGE FlexibleContexts #-}
module VecInsertionSort where

import           Control.Monad.ST
import           Data.Foldable (forM_)
import           Control.Monad (unless)
import qualified Data.Vector.Unboxed         as V
import qualified Data.Vector.Unboxed.Mutable as M

sort :: [Int] -> [Int]  -- sort on mutable arrays
sort list = runST $ do
    let listSize = length list
    vec <- V.thaw $ V.fromList list :: ST s (M.MVector s Int)

    forM_ [1..listSize - 1] $ \i -> do
        let jScan j
                | j >= 0 = do
                    cur  <- M.read vec j
                    next <- M.read vec (j + 1)
                    unless (cur <= next) $ do M.swap vec j (j + 1)
                                              jScan (j - 1)
                | otherwise = return ()
        jScan (i - 1)

    resVec <- V.freeze vec
    return $ V.toList resVec