The Forgotten

-|

Lecture 14

Cofree

Cofree is dual to Free.

data Free f a = Pure a | Free (f (Free f a))

data Cofree f a = a :< (f (Cofree f a))

But why dual??

Why is Reader dual to Env (Coreader)?

Why is Writer dual to Traced (Cowriter)?

Why is State (Reader composed with Writer) dual to Store (Costate, a.k.a. Env composed with Traced)?

Without delving into much category theory, the duality can be explained with adjunctions!

instance Functor f => Comonad (Cofree f) where
  extract    (x :<  _) = x
  extend f c@(_ :< xs) = f c :< (extend f <$> xs)

What other dualities can we observe? (spoiler: A LOT!!!!)

Adjoint functors (1/2)

A functor F is left adjoint to the functor G (conversely, G is right adjoint to F) if and only if for every a and b there exists a bijection between the sets of functions F(a) -> b and a -> G(b) (fig. 1) that is natural (fig. 2).

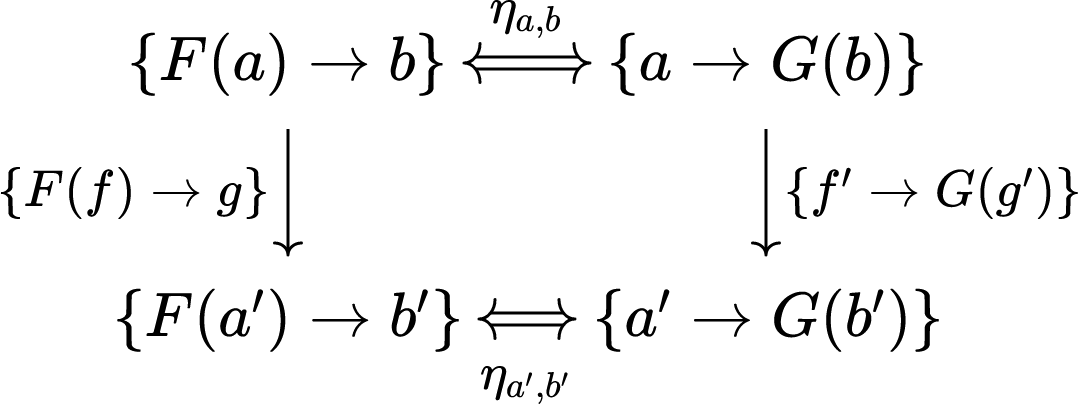
F \dashv G \iff \left\{ F(a) \to b \right\} \simeq \left\{ a \to G(b) \right\}

\forall f : a' \to a, g : b \to b',

Adjoint functors (2/2)

A functor F is left adjoint to the functor G (conversely, G is right adjoint to F) if and only if for every a and b there exist

a unit eta : a -> G(F(a)) and
a counit epsilon : F(G(b)) -> b of adjunction, such that:

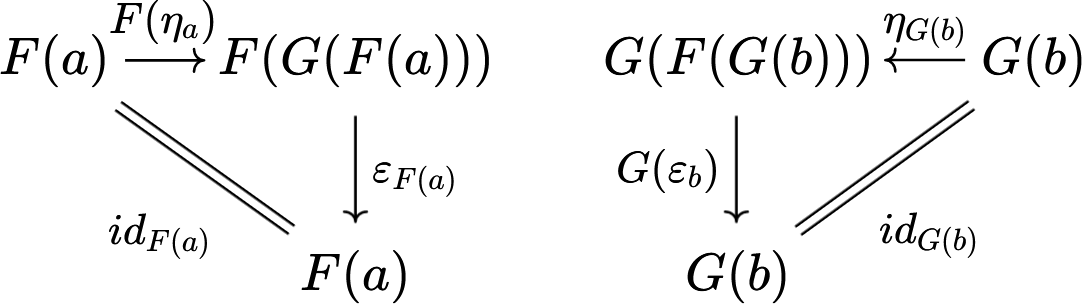
Why Adjunctions Matter: a lovely presentation by José Nuno Oliveira.

Adjoint functors in Haskell!

Let's not forget what subject this is :)

{-# LANGUAGE MultiparamTypeClasses #-}

class (Functor f, Functor g) => Adjunction f g where
  leftAdjunct  :: (f a -> b) -> (a -> g b)
  rightAdjunct :: (a -> g b) -> (f a -> b)
  unit   :: a -> g (f a)
  counit :: f (g b) -> b
  
  leftAdjunct f = fmap f . unit
  rightAdjunct g = counit . fmap g
  unit = leftAdjunct id
  counit = rightAdjunct id
  
  {-# MINIMAL unit, counit | leftAdjunct, rightAdjunct #-}

A handful of times defining the (co)unit in the instance is easier than defining the adjunctions. Hence we're gonna be focusing on them.

counit @(f a) . fmap @f (unit @a) ≡ id @(f a)
fmap @g (counit @a) . unit @(g b) ≡ id @(g b)

Edward Kmett's wondrous package for adjoint functors!

0 -| 1

{-# LANGUAGE DerivingFunctor, InstanceSigs, LambdaCase, MultiparamTypeClasses #-}

data Void1 p deriving Functor
 
data Unit1 p = Unit1 deriving Functor
 
instance Adjunction Void1 Unit1 where
  unit :: a -> Unit1 (Void1 a)
  unit _ = Unit1
 
  counit :: Void1 (Unit1 b) -> b
  counit = \case {}

Have you ever heard someone say that the empty datatype and the unit datatype are dual? Voila!

Sum -| Product

{-# LANGUAGE DerivingFunctor, InstanceSigs, LambdaCase, MultiparamTypeClasses #-}

data (f |+| g) a = Left1 (f a) | Right1 (g a) deriving Functor
 
data (f |*| g) a = f a :*: g a deriving Functor
 
instance (Adjunction f g, Adjunction f' g') => Adjunction (f |+| f') (g |*| g') where
  unit :: a -> (g |*| g') ((f |+| f') a)
  unit x = leftAdjunct Left1 x :*: leftAdjunct Right1 x
 
  counit :: (f |+| f') ((g |*| g') b) -> b
  counit = \case
    Left1 fp   -> rightAdjunct (\(gb :*: _) -> gb) fp
    Right1 f'p -> rightAdjunct (\(_ :*: g'b) -> g'b) f'p

This kind of explains the duality between Free and Cofree, but we'll get back to them in a jiffy.

Product -| Arrow

{-# LANGUAGE DerivingFunctor, InstanceSigs, MultiparamTypeClasses #-}

--                   Env     Reader
--                   Writer  Traced
instance Adjunction ((,) x) ((->) x) where
  unit :: a -> x -> (x, a)
  unit a = \x -> (x, a)
 
  counit :: (x, x -> b) -> b
  counit (x, f) = f x

Now you know.

Wait a moment. "unit" looks suspiciously like "return" for the State monad, and "counit" looks suspiciously like "extract" for the Store comonad.

Identity -| Identity

{-# LANGUAGE DerivingFunctor, InstanceSigs, MultiparamTypeClasses #-}

newtype IdentityT f a = IdentityT { runIdentityT :: f a } deriving Functor
 
instance Adjunction f g => Adjunction (IdentityT f) (IdentityT g) where
  unit :: a -> IdentityT g (IdentityT f a)
  unit = IdentityT . leftAdjunct IdentityT
 
  counit :: IdentityT f (IdentityT g b) -> b
  counit = rightAdjunct runIdentityT . runIdentityT

Composition -| Composition

{-# LANGUAGE DerivingFunctor, InstanceSigs, MultiparamTypeClasses #-}

newtype (g |.| f) a = Comp { runComp :: g (f a) } deriving Functor
 
instance (Adjunction f g, Adjunction f' g') => Adjunction (f' |.| f) (g |.| g') where
  unit :: a -> (g |.| g') ((f' |.| f) a)
  unit = Comp . leftAdjunct (leftAdjunct Comp)
 
  counit :: (f' |.| f) ((g |.| g') a) -> a
  counit = rightAdjunct (rightAdjunct runComp) . runComp

Free -| Cofree

{-# LANGUAGE DerivingFunctor, InstanceSigs, MultiparamTypeClasses #-}

data Free f a = Pure a | Free (f (Free f a)) deriving Functor
 
data Cofree f a = a :< f (Cofree f a) deriving Functor
 
instance Adjunction f g => Adjunction (Free f) (Cofree g) where
  unit :: a -> Cofree g (Free f a)
  unit x = Pure x 
        :< leftAdjunct (\funit -> leftAdjunct (\free -> Free (free <$ funit)) x) ()
 
  counit :: Free f (Cofree g a) -> a
  counit (Pure (a :< _)) = a 
  counit (Free ff) = error "IT'S A NIGHTMARE"

Look up Edward Kmett's definition of counit for this instance if you want a challenge.

Checkmate

One of the most basic, but astounding and yet understandable theorems of adjoint functors states that a (co)monad can be generated by composing them in their respective ways.

THE FINALE

\begin{align*} \bm{F \dashv G \implies} & \bm{G \circ F} \textbf{ is a \textit{monad} and} \\ & \bm{F \circ G} \textbf{ is a \textit{comonad}} \end{align*}

{-# LANGUAGE InstanceSigs, MultiparamTypeClasses, ScopedTypeVariables #-}

instance Adjunction f g => Monad (g |.| f) where
  return :: a -> (g |.| f) a
  return = Comp . unit
 
  (>>=) :: (g |.| f) a -> (a -> (g |.| f) b) -> (g |.| f) b
  c >>= f = joinComp $ fmap f c
    where
      joinComp :: (g |.| f) ((g |.| f) a) -> (g |.| f) a
      joinComp (Comp gfcgfa) = Comp $ fmap (counit . fmap runComp) gfcgfa
 
instance Adjunction f g => Comonad (f |.| g) where
  extract :: (f |.| g) a -> a
  extract = counit . runComp
 
  duplicate :: (f |.| g) a -> (f |.| g) ((f |.| g) a)
  duplicate (Comp fga) = Comp $ fmap (fmap Comp . unit) fga

And thus, State and Store are a monad and a comonad respectively.