let language = Haskell

in Lecture 2

Haskell features

Purity

Immutability

Static types

Non-null

Lazy evaluation

Playing with ghci (1 / 5)

GHCi — GHC Haskell REPL: interactively execute commands

$ stack repl      # you can also use 'stack ghci' to run 'ghci', or
$ cabal new-repl  # from inside project

<Some logging information, bla-bla-bla>
Prelude>  -- 'Prelude' prompt can be changed; slides use 'ghci>' prompt

ghci> 1 + 2 * 3
7
ghci> 3 / 5 * (7 + 1)
4.8
ghci> 2 ^ 16
65536
ghci> 1 + 1 == 3
False
ghci> 2 + 2 /= 5
True
ghci> 21 * 22 <= 20 * 23
False
ghci> 1 < 2 && 2 < 3
True
ghci> 0 > 0 || 10 >= 10
True

Basic arithmetic & boolens & comparisons

At least you can use Haskell as calculator!

Playing with ghci (2 / 5)

Calling functions in ghci: arguments separated by space character

ghci> not True
False
ghci> div 7 3  -- integral division (7 divide by 3)
2
ghci> max 3 5
5
ghci> min 6 (10 * 2)  -- not the same as 'min 6 10 * 2'
6

Personally I like space separated arguments; compare

max 1 2         // Haskell
std::max(1, 2)  // C++
Math.max(1, 2)  // Java

But you should think about arguments grouping

ghci> div 7 3 + 1
3
ghci> div 7 (3 + 1)
1
ghci> div 7 + 1 3
*** Compilation error!
ghci> div (7 + 1) 3
2

Playing with ghci (3 / 5)

Infix and Prefix call syntax:

* Both — operators and functions — can be called in prefix and infix

* Wrap operator in () to call in prefix

* Wrap function in `` (bacticks, ~ on keyboard) to call in infix

ghci> 3 + 4
7
ghci> (+) 3 4
7
ghci> mod 7 3    -- 7 modulo 3
1
ghci> 7 `mod` 3
1

Playing with ghci (4 / 5)

Assigning variables

-- Before GHC 8.0.1
ghci> let x = 3 + 5
ghci> x + 1
9

-- After GHC 8.0.1
ghci> x = 7 + 8
ghci> x * 2
30

String type

ghci> greeting = "Hello"
ghci> greeting ++ " world!"  -- use ++ instead of + to concatenate strings
"Hello world!"
ghci> "DONE: say \"" ++ greeting ++ " world!\"" 
"DONE: say "Hello world!""

Playing with ghci (5 / 5)

Types are important! Use `:t` command to see type in GHCi

ghci> :t 'x'
'x' :: Char
ghci> :t False
False :: Bool
ghci> :t not
not :: Bool -> Bool
ghci> :t (&&)
(&&) :: Bool -> Bool -> Bool
ghci> :t 42
42 :: Num t => t  -- numeric constants are polymorphic;
                  -- we will get to that later

Use `:set +t` command to show types after each command

ghci> :set +t
ghci> 'x'
'x'
it :: Char
ghci> False || True
True
it :: Bool
ghci> let x = False
x :: Bool

Function declaration

-- This function adds first number to product of second and third
addMul :: Int -> Int -> Int -> Int  -- This is type signature of 'addMul'
addMul x y z = x + y * z            -- This is definition     of 'addMul'

-- Btw, single-line comments start with --
greet :: String -> String
greet name = "Hello, " ++ name ++ "!"

Let's create our functions! Put next code into 'Lecture.hs' file

$ stack ghci  # from folder where 'Lecture.hs' is
ghci> :l Lecture.hs  -- :l is short form of :load command
ghci> addMul 1 2 3
7
ghci> greet "Haskell World"
"Hello, Haskell World!"

Reminder: arguments grouping

addMul 1 2  3 + 1
addMul 1 2 (3 + 1)
addMul 1 (1 + 1) 3
addMul 1  1 + 1  3

Telephone

infixr 1 ==>  -- specify associativity for 'implies' operator
(==>) :: Bool -> Bool -> Bool
a ==> b = not a || b

In Haskell you can create your own operators! It doesn't mean you should... But sometimes they are really handy.

ghci> False ==> False ==> False
True
ghci> False ==> (False ==> False)
True
ghci> (False ==> False) ==> False
False

[infix|infixl|infixr] <precedence ∈ [0..10)> [operators]

-- somewhere in 'base'
infixr 2 ||
(||) :: Bool -> Bool -> Bool

Function application — space — has highest precedence 10.

ghci> True || True  ==> False
???
ghci> True || (True ==> False)
???

ghci> True || True  ==> False
False
ghci> True || (True ==> False)
True


infixr 3 &&
(&&) :: Bool -> Bool -> Bool

Haskell association

\mathrm{infixl} : a \ \circ \ b \ \circ \ c \ \circ \ d \ \equiv ((a \ \circ \ b) \ \circ \ c) \ \circ \ d

\mathrm{infixr} : a \ \circ \ b \ \circ \ c \ \circ \ d \ \equiv a \ \circ \ (b \ \circ \ (c \ \circ \ d))

\mathrm{infix} : a \ \circ \ b \ \circ \ c \ \circ \ d \ \equiv Compilation\ error

Important type: List

ghci> [1 + 2, 3 + 4, 5 * 6]  -- comma-separated
[3,7,30]

Linked lists: homogeneous collection of elements

ghci> let list = [2, 1, 3]  -- create list variable
ghci> [5, 10] ++ list       -- concatenate lists with ++ operator
[5, 10, 2, 1, 3]
ghci> 10 : list             -- : operator adds element to the beginning of list
[10, 2, 1, 3]

ghci> list
[2, 1, 3]
ghci> reverse list  -- this doesn't change 'list'
[3, 1, 2]
ghci> list
[2, 1, 3]
ghci> let anotherList = 5 : list  -- new variable to save changes
ghci> anotherList
[5, 2, 1, 3]
ghci> list
[2, 1, 3]

All variables in Haskell are immutable by default!

More lists examples

emptyList     :: [Int]
emptyList      = []

listExample   :: [Int]
listExample    = [2, 1, 3]                       -- 2:1:3:[]

singletonList :: [Int]
singletonList  = 1 : emptyList                   -- or simply [1]

listExample'   = 5:10:listExample                -- [5, 10, 2, 1, 3]

twoLists       = singletonList ++ listExample    -- [1, 2, 1, 3]

trinity        = listExample ++ [7] ++ twoLists  -- [2, 1, 3, 7, 1, 2, 1, 3]

string        :: [Char]  -- extremely inefficent representation of String
string         = "str"                           -- ['s', 't', 'r']

otherString   :: String                          -- other name for [Char]
otherString    = "other " ++ string              -- "other str"

ghci> "" == []
True

JavaScript: «Miss me?»

Ranges

Java 8

IntStream.range(0, 5).toArray();                    // {0, 1, 2, 3, 4};
IntStream.rangeClosed(0, 5).toArray();              // {0, 1, 2, 3, 4, 5};
IntStream.iterate(0, x -> x + 2).limit(5).toArray() // {0, 2, 4, 6, 8};

Kotlin

0..5        // 0, 1, 2, 3, 4, 5
0 until 5   // 0, 1, 2, 3, 4
0..5 step 2 // 0, 2, 4

Haskell

[0 .. 5]     -- [0, 1, 2, 3, 4, 5]
[1, 3 .. 5]  -- [1, 3, 5, 7]
[0..]        -- [0, 1, 2, 3, ...] : infinite list
[0, 2 ..]    -- [0, 2, 4, 6, ...] : all even numbers
[5, 4 .. 1]  -- [5, 4, 3, 2, 1]
[5 .. 1]     -- [] — empty list

Python

range(5)       # 0, 1, 2, 3, 4
range(1, 5)    # 1, 2, 3, 4
range(1, 5, 2) # 1, 3

Lists Functions (1 / 3)

ghci> let l = [2, 1, 3]
ghci> head l
2
ghci> tail l
[1, 3]
ghci> last l
3
ghci> init l
[2, 1]

Accessing elements of list

But try not to use these functions...

Lists Functions (2 / 3)

ghci> drop 2 [2, 1, 3]
[3]

ghci> [2, 1, 3] !! 2  -- l !! i ≡ l[i], O(i) time
3

Functions from Prelude

And moar: takeWhile, splitAt, iterate, reverse, lines, unlines, etc. Prelude has a lot of functions and operators to work with lists.

ghci> take 1 [2, 1, 3]
[2]

ghci> replicate 3 [1..5]
[[1,2,3,4,5], [1,2,3,4,5], [1,2,3,4,5]]

ghci> zip [1,2,3] "abc"
[(1, 'a'), (2, 'b'), (3, 'c')]  -- (1, 'a') is pair of type (Int, Char)

ghci> unzip [(5, True), (10, False)]
([5, 10], [True, False])

ghci> words "Hello,    Haskell  \t\n\n   world!"
["Hello,", "Haskell", "world!"]

ghci> unwords ["Hello,", "Haskell", "world!"]
"Hello, Haskell world!"

Statements & expressions

void f();  // function definition is statement

int random() {
    return 4;  // `return` is statement, 4 is expression
}

int main() {
    int a = random(); // variable declaration: statement, `random()` is expression
    if (a > 0) {  // `if` operator is statement, `a > 0` is expression
        printf("Wow, such C++");  // statement, or?...
    }
}

С++

Common statements in imperative languages are expressions in Haskell

let expression

pythagoras :: Int -> Int -> Int
pythagoras x y = x^2 + y^2

let <bindings> in <expression>

pythagoras(x, y) = x^2 + y^2

Let's implement with let:

Already can do it in simple way!

With let

pythagoras :: Int -> Int -> Int
pythagoras x y = let x2 = x ^ 2  -- Alignment is EXTREMELY IMPORTANT!!!
                     y2 = y ^ 2  -- No tabs, only spaces!
                 in x2 + y2

Haskell is layout-sensitive language.

It means that ugly code won't compile.

let in files and in ghci

ghci> let x = 10  -- saves variable 'x', doesn't print it
ghci> x
10

ghci> let y = 1 + 3 in y  -- doesn't save variable 'y', prints result immediately
4
ghci> y

<interactive>:41:1: error: Variable not in scope: y

Believe me, there's a reason to have several ways to assign variables in ghci

where clause

pythagoras :: Double -> Double -> Double
pythagoras a b = a2 + b2
  where  -- details of implementation are inside 'where'
    square x = x ^ 2
    a2       = square a
    b2       = square b

Haskell

Java

double pythagoras(double a, double b) {
    class Squarer { 
        double eval(double x) { return x * x; }
    }
    final double a2 = new Squarer().eval(a);
    final double b2 = new Squarer().eval(b);

    return a2 + b2;
}

You want to define local functions or variables to: (1) not spoil global namespace or (2) for optimization purposes (in Haskell)

Difference between let and where?

link

if expression

factorial :: Integer -> Integer  -- arbitrary precision integer type
factorial n = if n <= 1 
              then 1 
              else n * factorial (n - 1)  -- this implementation is 
                                          -- extremely inefficient

if <predicate>

then <expression if predicate is True>

else <expression if predicate is False>

So it's more like ternary operator

Side note: use Natural from `Numeric.Natural` instead of Integer if you only mean non-negative (≥ 0) integers (like in example above)

guards

public int collatzSum(int n) {
    if (n < 0) 
        return 0;
    else if (n == 1) 
        return 1;
    else if (n % 2 == 0) 
        return n + collatzSum(n / 2);
    else 
        return n + collatzSum(3 * n + 1);
}

Java

collatzSum :: Natural -> Natural
collatzSum n
    | n == 1    = 1
    | even n    = n + collatzSum (n `div` 2)
    | otherwise = n + collatzSum (3 * n + 1)

Haskell

otherwise :: Bool
otherwise = True

What is otherwise?

case expression

public String getFont(int fontConstant) {
    String font = null;
    switch (fontConstant) {
        case 0: font = "PLAIN";  break;
        case 1: font = "BOLD";   break;
        case 2: font = "ITALIC"; break;
        default: font = "UNKNOWN";
    }
    return font;
}

Java

Haskell

getFont :: Int -> String
getFont n = case n of
                 0 -> "PLAIN"
                 1 -> "BOLD"
                 2 -> "ITALIC"
                 _ -> "UNKNOWN"

caseOperation 
  :: Char -> Int -> Int -> Int
caseOperation op x y = 
    case op of
         '+' -> x + y
         '-' -> x - y
         _   -> 0   -- _ should be 
                    -- under ' and 
                    -- not under -

case <expression> of

[<pattern> → <expression>]

inc, dec :: Int -> Int
inc x = x + 1
dec x = x - 1

HOF: Higher order functions

Function in Haskell is a first class object. It means that you can pass functions as arguments to other functions.

changeTwiceBy :: (Int -> Int) -> Int -> Int
changeTwiceBy operation value = operation (operation value)

ghci> changeTwiceBy inc 5
7
ghci> changeTwiceBy dec 5
3

Lambdas: anonymous fun

\arg1 arg2 ... argN → <expression>

ghci> changeTwiceBy (\x -> x + 1) 5
7
ghci> changeTwiceBy (\x -> x * 2) 5
20

tripleApply :: (Int -> Int -> Int) -> Int -> Int
tripleApply f x = (x `f` x) `f` (x `f` x)

ghci> tripleApply (\x y -> x ^ y) 2
256

ghci> tripleApply (^) 2  -- you can pass operators as functions
256

Without lambda

Polymorphism

Polymorphic functions

first :: a -> a -> a
first x y = x

public <T> T first(T x, T y) {
    return x;
}

Java

Haskell

parametric polymorphism vs. ad-hoc polymorphism

overloading?

Parametric polymorphism refers to when the type of a value contains one or more (unconstrained) type variables, so that the value may adopt any type that results from substituting those variables with concrete types.

Wiki: Polymorphism

Polymorphic examples

id :: a -> a
id x = x

fst :: (a, b) -> a
snd :: (a, b) -> b

emptyList :: [a]
emptyList = []

repeatThree :: a -> [a]
repeatThree x = [x, x, x]

ghci> repeatThree 'x'
"xxx"
it :: [Char]
ghci> repeatThree True
[True, True, True] 
it :: [Bool]

ghci> tripleApply (^) 2
256
ghci> tripleApply (++) [3,1]
[3, 1, 3, 1, 3, 1, 3, 1]

tripleApply :: (a -> a -> a) -> a -> a
tripleApply f x = f (f x x) (f x x)

HOF Polymorphism

map     :: (a -> b)      -> [a] -> [b]
filter  :: (a -> Bool)   -> [a] -> [a]
foldr1  :: (a -> a -> a) -> [a] ->  a
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]

ghci> map negate [2, 1, 3]
[-2,-1,-3]

ghci> filter odd [1,2,3,4,5]  
[1,3,5]

ghci> foldr1 (+) [1,2,4]  -- sum [1,2,4]
7

ghci> takeWhile isUpper "HTMLXml"
"HTMLX"

ghci> zipWith max [1..5] [5, 4 .. 1]
[5,4,3,4,5]

HOF, Polymophism & Tuples

uncurry :: (a -> b -> c) -> (a, b) -> c
uncurry f p = f (fst p) (snd p)

ghci> uncurry (+) (3, 4)
7

ghci> curry fst 3 4
3
ghci> curry snd 3 4
4

Currying:Partial application (1/ 2)

Functions in Haskell are very simple! They have only one argument and one result. Function arrow is right-associative.

bar :: (Int -> Int) ->  Int -> Int
bar :: (Int -> Int) -> (Int -> Int)  -- ^ these two bars are the same

evilBar :: (Int -> Int) -> Int -> Int
evilBar :: Int  -> Int  -> Int -> Int  -- ^ and these two are not

foo :: Int ->  Char ->  String ->  Double
foo :: Int -> (Char -> (String -> (Double))

foo, bar :: Int -> String
foo x = show x
bar   = show

Currying:Partial application (2/ 2)

-- monomoprhic 'div'
div :: Int -> (Int -> Int)

Works with operators!

ghci> map (+2) [2, 1, 3]
[4, 3, 5]
ghci> filter (<3) [1..5]
[1, 2]
ghci> filter (3<) [1..5]
[4, 5]

-- div7By is partially applied div
ghci> div7By = div (7 :: Int)
div7By :: Int -> Int

ghci> div7By 2
3
ghci> div7By 3
2

ghci> (div 7) 3
2

ghci> map (div 7) [1..7]
[7,3,2,1,1,1,1]

Note on currying (-) operator

ghci> map (5+) [1..5]
[6, 7, 8, 9, 10]
ghci> map (+5) [1..5]
[6, 7, 8, 9, 10]

You can partially apply (+) operator without problems

But you can't do the same with (-) operator because (-5) is a constant

ghci> map (5-) [1..5]
[4,3,2,1,0]
ghci> map (-5) [1..5]

    • Non type-variable argument in the constraint: Num (a -> b)
      (Use FlexibleContexts to permit this)
    • When checking the inferred type
        it :: forall a b. (Enum a, Num (a -> b), Num a) => [b]

Use `subtract` function instead

ghci> subtract 5 3
-2
ghci> map (subtract 5) [1..5]
[-4, -3, -2, -1, 0]

Flip

flip :: (a -> b -> c) -> b -> a -> c
flip f b a = f a b

When you finally understand flip

show2 :: Int -> Int -> String
show2 x y = show x ++ " and " ++ show y

showSnd, showFst, showFst' 
    :: Int -> String
showSnd  = show2 1
showFst  = flip show2 2
showFst' = (`show2` 2)

ghci> showSnd 10
"1 and 10"

ghci> showFst 10
"10 and 2"

ghci> showFst' 42
"42 and 2"

Hindley-Milner exercise: type w/o ghci

ghci> :t flip id
???

ghci> :t flip id
flip id :: b -> (b -> c) -> c

Pattern matching

fact :: Integer -> Integer
fact 0 = 1
fact n = n * fact (n - 1)

map :: (a -> b) -> [a] -> [b]
map _    []  = []
map f (x:xs) = f x : map f xs -- [2, 1, 3] == 2 : 1 : 3 : []

sumList3 :: [Int] -> Int
sumList3 [x, y, z] = x + y + z
sumList3 _         = 0

puzzle :: [Int] -> [Int]
puzzle (x:xs@(y:z:_)) = if x < y && y > z then y : c else c
  where 
    c = puzzle xs
puzzle _ = []

dropWhile :: (a -> Bool) -> [a] -> [a]
dropWhile _      []  = []
dropWhile p l@(x:xs) = if p x then dropWhile p xs else l

stringLit :: String -> String
stringLit "such" = "pattern" 
stringLit "much" = "amaze" 
stringLit x      = "wow"

LANGUAGE: what?

Some Haskell features are not enabled by default. They can be enabled by so-called 'language pragmas'.

-- in ghci
ghci> :set -X<NameOfPragma>

ghci> map (\x -> (42, x)) [1..5]
[(42,1), (42,2), (42,3), (42,4), (42,5)]
ghci> map (\x -> (x, 42)) [1..5]
[(1,42), (2,42), (3,42), (4,42), (5,42)]

Example: you want to pair each element of list with 42.

Dark side

ghci> :set -XTupleSections

ghci> map (42,) [1..5]
[(42,1), (42,2), (42,3), (42,4), (42,5)]

ghci> map (,42) [1..5]
[(1,42), (2,42), (3,42), (4,42), (5,42)]

Light side: TupleSections

Some syntax extensions: Part 1

Some syntax extensions: Part 2

-- in MyModule.hs
{-# LANGUAGE NameOfPragma #-}

Several more nice syntaxes

-XLambdaCase

veryLongFunctionName :: Int -> String
veryLongFunctionName 0 = foo
veryLongFunctionName 1 = bar
veryLongFunctionName n = baz n

{-# LANGUAGE LambdaCase #-}

veryLongFunctionName :: Int -> String
veryLongFunctionName = \case
    0 -> foo
    1 -> bar
    n -> baz n

-- syntax sugar for
veryLongFunctionName :: Int -> String
veryLongFunctionName x = case x of
    0 -> foo
    1 -> bar
    n -> baz n

-XViewPatterns

exactTwoWords :: String -> Bool
exactTwoWords s = case words s of
    [_, _] -> True
    _      -> False

{-# LANGUAGE ViewPatterns #-}

exactTwoWords :: String -> Bool
exactTwoWords (words -> [_, _]) = True
exactTwoWords _                 = False

Function application (1 / 2)

infixr 0 $
($) :: (a -> b) -> a -> b  -- function application
f $ x = f x

In Functional programming everything is a function. Even function application — space ' ' — is function. What if...

Why? Useful to remove ()

foo, bar :: [Int] -> Int
foo list = length (filter odd (map (div 2) (filter even (map (div 7) list))))
bar list = length $ filter odd $ map (div 2) $ filter even $ map (div 7) list

ghci> length [0..5]
6
ghci> length $ [0..5]
6

Function application (2 / 2)

ghci> let funs = [(+2), div 7, (*5)]
funs :: [Integer -> Integer]
ghci> let vals = [20, 30, 40]
vals :: [Integer]
ghci> :t zipWith
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
ghci> zipWith ($) funs vals
[22, 0, 200] 
ghci> zipWith id funs vals
[22, 0, 200]

Reverse application

infixl 1 &
(&) :: a -> (a -> b) -> b  -- in 'Data.Function' module
x & f = f x

($) :: (a -> b) -> a -> b
(&) :: a -> (a -> b) -> b
(&) = flip ($)

ghci> (\l -> l ++ reverse l) [2,1,3]
[2,1,3,3,1,2]
ghci> [2,1,3] & \l -> l ++ reverse l  -- useful for removing parenthesis
[2,1,3,3,1,2]

Function composion (1 / 3)

infixr 9 .
(.) :: (b -> c) -> (a -> b) -> (a -> c)  -- same as (b -> c) -> (a -> b) -> a -> c
f . g = \x -> f (g x)

incNegate :: Int -> Int
incNegate x = negate (x + 1)

incNegate x = negate $ x + 1

incNegate x = (negate . (+1)) x

incNegate x = negate . (+1) $ x

incNegate   = negate . (+1)  -- η-reduce

Must see:

YouTube: Point-Free or Die: Tacit Programming in Haskell and Beyond - Amar Shah

"outside . inside" is a composition

1. \x -> outside (inside x)
2. \x -> outside $ inside x
3. \x -> outside . inside $ x
4.       outside . inside

Function composion (2 / 3)

foo, bar :: [Int] -> Int
foo patak = length $ filter odd $ map (div 2) $ filter even $ map (div 7) patak
bar       = length . filter odd . map (div 2) . filter even . map (div 7)

Don't need to keep names of variables in mind

Instead of specifying what to do with variables, you specify how data should be transformed

stringsTransform :: [String] -> [String]
stringsTransform l = map (\s -> map toUpper s) (filter (\s -> length s == 5) l)

stringsTransform l = map (\s -> map toUpper s) $ filter (\s -> length s == 5) l

stringsTransform l = map (map toUpper) $ filter ((== 5) . length) l

stringsTransform = map (map toUpper) . filter ((== 5) . length)

Simplifying complex function

Pointless functions

Function composion (3 / 3)

stringsTransform :: [String] -> [String]
stringsTransform l = map (\s -> map toUpper s) (filter (\s -> length s == 5) l)

stringsTransform l = map (\s -> map toUpper s) $ filter (\s -> length s == 5) l

stringsTransform l = map (map toUpper) $ filter ((== 5) . length) l

stringsTransform = map (map toUpper) . filter ((== 5) . length)

Simplifying complex function

Pointless functions

List comprehension

ghci> [x | x <- [1..10], even x]
[2,4,6,8,10]

quickSort :: [Int] -> [Int]
quickSort [] = []
quickSort (x:xs) 
    = quickSort [y | y <- xs, y <= x] ++ [x] ++ quickSort [y | y <- xs, y > x]

ghci> filter even [1..10]
[2,4,6,8,10]

ghci> [if even x then "!" else "?" | x <- [1 .. 5]] 
["?","!","?","!","?"]

ghci> [ x * y | x <- [1, 3, 5], y <- [2, 4, 6], x * y >= 10]
[12,18,10,20,30]

ghci> [13 | even 13]  -- conditionally create singleton list
[]
ghci> [14 | even 14]
[14]

Lazy evaluation

Lazy evaluation order

square x = x*x

square (1+2)

square (1+2)
=> (1+2)*(1+2)

(1+2)*(1+2)
=> 3*(1+2)
=> 3*3
=> 9

Evaluated (1+2) twice :(

Expression graph

Every expression can be represented as a graph

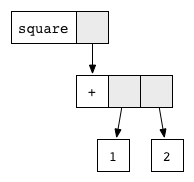
Every function corresponds to a reduction rule

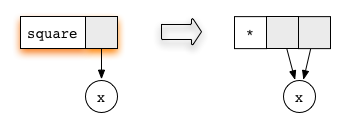
No reduction rule for constructor

Lazy evaluation of graph

Lazy evaluation always tries to reduce the topmost function application first

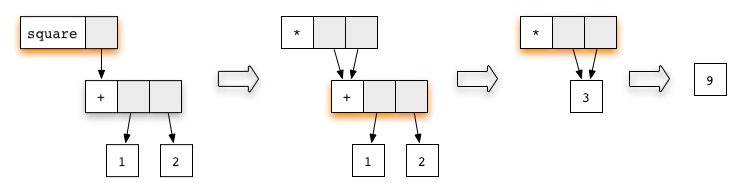
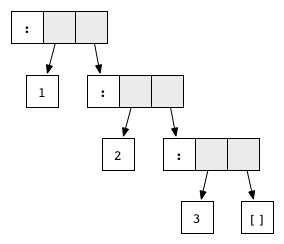
No unevaluated redexes and graph represents the list 1:2:3:[].

Normal form

NF: all sub-expressions are evaluated

42

(2, "hello")

\x -> (x + 1)

NF

No NF

1 + 2

(\x -> x + 1) 2

"he" ++ "llo"

(1 + 1, 2 + 2)

Weak head normal form

10

2 : [1, 3]

'h' : ("e" ++ "llo")

[1, 2 * 2, 3 ^ 3]

[4, length undefined]

Just (2 + 7)

(1 + 2, 3 + 4)

\x -> x + 10

\zx -> foldr (+) zx [1, 2, 3]

WHNF (in Haskell): outermost must be either constructor or lambda

WHNF

No WHNF

1 + 1

1 + (2 + 3)

(\x -> x + 10) 3

length [1, 2, 3]

Just (2 + 7) >>= 
    \n -> Just $ n * 2

Why is it important?

Pattern matching requires evaluation to WHNF!

fromJust' :: Maybe a -> Int
fromJust' (Just a) = 10

ghci> fromJust' undefined
*** Exception: Prelude.undefined

first :: Int -> Int -> Int
first x _ = x

zeroF :: Int -> Int -> Int
zeroF x 0 = x
zeroF _ y = y

ghci> fromJust' $ Just undefined
10

ghci> first 10 undefined
10

ghci> zeroF 10 undefined
*** Exception: Prelude.undefined

thunk

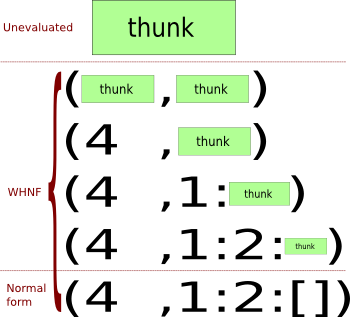
Evaluating (4, [1,2]) step by step

Time: Lazy evaluation never performs more evaluation steps than eager evaluation.

Time & Space

Space: Memory used by an unevaluated expression may differ significantly from the memory used by its normal form

((((0 + 1) + 2) + 3) + 4)

It is called a space leak

Infinite lists

ghci> [1..]
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,
31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,
58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,
85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,
109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,
129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,
149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,
169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187, ...

Lists in Haskell can be infinite. But only required part is evaluated.

ghci> repeat 1
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, ...

ghci> take 5 [1..]
[1,2,3,4,5]
ghci> zip [0..] "abacaba"
[(0,'a'), (1,'b'), (2,'a'), (3,'c'), (4,'a'), (5,'b'), (6,'a')]

Types + lazy evaluation

-- | @'fix' f@ is the least fixed point of the function @f@,
-- i.e. the least defined @x@ such that @f x = x@.
fix :: (a -> a) -> a
fix f = let x = f x in x

fix point combinator

ghci> fix id
<hangs>

fix :: (a        -> a       ) -> a        [1]
fix :: ((b -> c) -> (b -> c)) -> (b -> c) [2]
fix :: ((b -> c) ->  b -> c ) -> b -> c   [3]

import Data.Function (fix)

fixLen :: [a] -> Int
fixLen = fix $ \f l -> case l of
    []     -> 0
    (x:xs) -> 1 + f xs

ghci> fixLen [1..5]
5

Grokking fix

Small challenge: implement fixLen using accumulator

Classical lazy examples (1 / 3)

Eratosthene sieve

primes :: [Int]
primes = filterPrime [2..] 
  where 
    filterPrime (p:xs) = p : filterPrime [x | x <- xs, x `mod` p /= 0]

ghci> take 15 primes 
[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47]

Classical lazy examples (2 / 3)

Fibonacci numbers

fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (drop 1 fibs)

fib :: Int -> Int
fib n = fibs !! n

ghci> take 10 fibs
[0,1,1,2,3,5,8,13,21,34]
ghci> fib 50
12586269025

Lazy dynamic programming

Puzzles on pointless

q1 = filter (even . length)

q2 = filter (odd . sum . take 5) . map (replicate 10)

q3 = length . filter id . map even  -- id x = x

q4 = (. length) . (+)

Useful links

LearnYouAHaskell (chapters 2, 4-7)

FPComplete: 10 things you should know about Haskell syntax

let language = Haskell

in Lecture 2

Haskell features

Playing with ghci (1 / 5)

Playing with ghci (2 / 5)

Playing with ghci (3 / 5)

Playing with ghci (4 / 5)

Playing with ghci (5 / 5)

Function declaration

Telephone

Haskell association

Important type: List

More lists examples

JavaScript: «Miss me?»

Ranges

Lists Functions (1 / 3)

But try not to use these functions...

Lists Functions (2 / 3)

Statements & expressions

let expression

let in files and in ghci

where clause

if expression

guards

case expression

HOF: Higher order functions

Lambdas: anonymous fun

Polymorphism

Polymorphic functions

Parametric polymorphism refers to when the type of a value contains one or more (unconstrained) type variables, so that the value may adopt any type that results from substituting those variables with concrete types.

Wiki: Polymorphism

Polymorphic examples

HOF Polymorphism

HOF, Polymophism & Tuples

Currying:Partial application (1/ 2)

Currying:Partial application (2/ 2)

Note on currying (-) operator

Flip

Hindley-Milner exercise: type w/o ghci

Pattern matching

LANGUAGE: what?

Dark side

Light side: TupleSections

Several more nice syntaxes

-XLambdaCase

-XViewPatterns

Function application (1 / 2)

Function application (2 / 2)

Function composion (1 / 3)

Function composion (2 / 3)

Pointless functions

Function composion (3 / 3)

Pointless functions

List comprehension

Lazy evaluation

Lazy evaluation order

Expression graph

Lazy evaluation of graph

Normal form

NF: all sub-expressions are evaluated

NF

No NF

Weak head normal form

WHNF (in Haskell): outermost must be either constructor or lambda

WHNF

No WHNF

Why is it important?

Pattern matching requires evaluation to WHNF!

*thunk*

Evaluating (4, [1,2]) step by step

Time & Space

Infinite lists

Types + lazy evaluation

fix point combinator

Grokking fix

Classical lazy examples (1 / 3)

Eratosthene sieve

Classical lazy examples (2 / 3)

Fibonacci numbers

Puzzles on pointless

thunk