Lecture 4

<$> Functor

<*> Applicative

Table of contents

Semigroup, Monoid

Foldable

Functor

Applicative

Alternative

Traversable

Phantom types

Type extensions

Semigroup, Monoid

OOP vs. Math

-- actually in 'base'
class Semigroup m where
    (<>) :: m -> m -> m
Associativity law for Semigroup: 
  1. (x <> y) <> z ≡ x <> (y <> z)
1. (++)
2. max/min
3. (+)
4. (*)

Semigroups

Monoids

-- also in 'base' but...
class Semigroup m => Monoid m where
    mempty :: m
Identity laws for Monoid: 
  2. x <> mempty ≡ x
  3. mempty <> x ≡ x
1. (++)
2. (+)
3. (*)

Semigroup & its List instance

Semigroup typeclass

class Semigroup a where
    (<>)    :: a -> a -> a
    sconcat :: NonEmpty a -> a
    stimes  :: Integral b => b -> a -> a
instance Semigroup [a] where
    (<>) = (++)
ghci> [1..5] <> [2,4..10]
[1,2,3,4,5,2,4,6,8,10]
>>> 3 * list(range(1,6))
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

Python

ghci> concat (replicate 3 [1..5])
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

Haskell

Super Haskellgon!

ghci> 3 `stimes` [1..5]
[1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5]

SO: How to use replicate to generate matrix?

Semigroup: numeric instances

instance Semigroup Int where
    -- Which one to choose?
    1. (<>) = (+)
    2. (<>) = (*)

We can combine numbers as well. But how?

newtype Sum     a = Sum     { getSum     :: a }
newtype Product a = Product { getProduct :: a }
instance Num a => Semigroup (Sum a) where
  Sum x <> Sum y = Sum (x + y)

instance Num a => Semigroup (Product a) where
  Product x <> Product y = Product (x * y)

The Haskell way: emulate multiple instances for one type with multiple newtypes (wrappers)

ghci> 3 <> 5 :: Sum Int
Sum { getSum = 8 }
ghci> 3 <> 5 :: Product Int
Product { getProduct = 15 }

More Semigroup instances

newtype Max   a = Max   { getMax   :: a    }  -- max
newtype Min   a = Min   { getMin   :: a    }  -- min
newtype Any     = Any   { getAny   :: Bool }  -- ||
newtype All     = All   { getAll   :: Bool }  -- &&
newtype First a = First { getFirst :: a }     -- first value
newtype Last  a = Last  { getLast  :: a }     -- last value

Use the same approach for different situations

ghci> Max 3 <> Max 10 <> Max 2
Max { getMax = 10 }
ghci> Min 3 <> Min 10 <> Min 2
Min { getMin = 2 }

ghci> Any True <> Any False <> Any True
Any { getAny = True }
ghci> All True <> All False <> All True
All { getAll = False }

ghci> First Nothing <> First (Just 10) <> First (Just 1)
First { getFirst = Nothing }
ghci> Last [] <> Last [5, 3, 6] <> Last [11, 9 .. -5]
Last { getLast = [11, 9 .. -5] }

One <> to rule them all

Enter: Monoid!

class Semigroup a => Monoid a where
    mempty  :: a
    mappend :: a -> a -> a -- (<>) by default
    mconcat :: [a] -> a

Monoid typeclass 

instance Monoid [a] where
    mempty = []

And all the rest is almost the same.

instance (Monoid a, Monoid b) => Monoid (a, b) where
                         mempty = (         mempty,          mempty)
    (a1, b1) `mappend` (a2, b2) = (a1 `mappend` a2, b1 `mappend` b2)

Monoids tour

instance Num a => Monoid (Sum a) where
    mempty = Sum 0

instance Num a => Monoid (Product a) where
    mempty = Product 1

More Monoid instances

newtype Any     = Any   { getAny   :: Bool }    -- ||, mempty = False
newtype All     = All   { getAll   :: Bool }    -- &&, mempty = True
newtype First a = First { getFirst :: Maybe a } -- first Just, mempty = Nothing
newtype Last  a = Last  { getLast  :: Maybe a } -- last Just, mempty = Nothing
ghci> mempty <> First (Just 10) <> First (Just 1)
First { getFirst = Just 10 }
ghci> Last (Just 31) <> Last (Just 22) <> mempty
Last { getLast = Just 22 }

One mempty to rule the universe

Two more important Monoids

newtype Dual a = Dual { getDual :: a }       -- passes the arguments of (<>)
                                             -- in REVERSE order
newtype Endo a = Endo { appEndo :: a -> a }  -- the monoid of endomorphisms on 'a' 
instance Semigroup a => Semigroup (Dual a) where
  Dual x <> Dual y = Dual (y <> x)
  
instance Monoid a => Monoid (Dual a) where
  mempty = Dual mempty
instance Semigroup (Endo a) where
  Endo f <> Endo g = Endo (f . g)
  
instance Monoid (Endo a) where
  mempty = Endo id

Beyond Monoid & to the stars!

Picture

Most mind-blowing Haskell article about algebraic structures

Foldable

foldr and foldl 

foldr :: (a -> b -> b) -> b -> [a] -> b
foldl :: (b -> a -> b) -> b -> [a] -> b

Eliminating (recursing on) a list

foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b

Generalization for arbitrary containers

ghci> foldr (+) 0 [2, 1, 10]
13
ghci> foldr (*) 3 [2, 1, 10]
60
foldr (\s rest -> rest + length s) 0 ["aaa", "bbb", "s"]
foldr (\rest s -> rest + length s) 0 ["aaa", "bbb", "s"]

Which one is correct?

Foldable typeclass

-- | Simplified version of Foldable
class Foldable t where
    {-# MINIMAL foldMap | foldr #-}

    fold    :: Monoid m => t m -> m
    foldMap :: Monoid m => (a -> m) -> t a -> m
    foldr   :: (a -> b -> b) -> b -> t a -> b

Some basic instances

instance Foldable [] where
    foldr :: (a -> b -> b) -> b -> [a] -> b
    foldr _ z []     =  z
    foldr f z (x:xs) =  x `f` foldr f z xs
instance Foldable Maybe where
    foldr :: (a -> b -> b) -> b -> Maybe a -> b
    foldr _ z Nothing  = z
    foldr f z (Just x) = f x z

Reasons to drop Haskell

ghci> length (4, [1,2,3])
???

Reddit — Proposal: Suggest explicit TypeApplication for Foldable

ghci> foldr (+) 1 (Just 3)
4
ghci> foldr (+) 0 Nothing
0
ghci> length (4, [1,2,3])
1

Grokking foldr

foldr (+) 0 (1 : 2 : 3 : []) ≡ 
             1 + 2 + 3 + 0

Think of folds as replacing constructors, i.e. ':', '[]', with functions/values.

simple-reflect

ghci> import Debug.SimpleReflect
ghci> sum [1..5] :: Expr 
0 + 1 + 2 + 3 + 4 + 5
ghci> foldr f x [a,b,c]
f a ( f b ( f c x ) )

Pretty foldr picture (@skore_de on Twitter)

Functor

Apply a function to a value wrapped in a container?

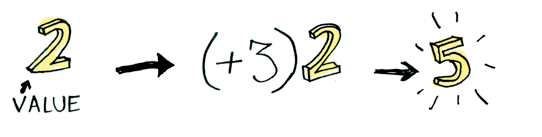
ghci> fmap (+3) (Just 2)
Just 5
ghci> fmap (+3) Nothing
Nothing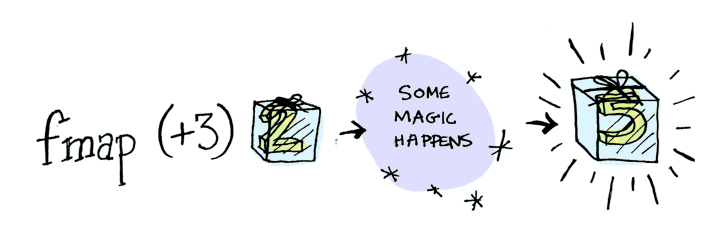

Functor

class Functor f where               -- f :: Type -> Type
    fmap :: (a -> b) -> f a -> f b

Functor laws 

1. Identity 
   fmap id      ≡ id
2. Composition
   fmap (f . g) ≡ fmap f . fmap g

These two laws state that fmap is a homomorphism that preserves composition and identities.

The Maybe Functor 

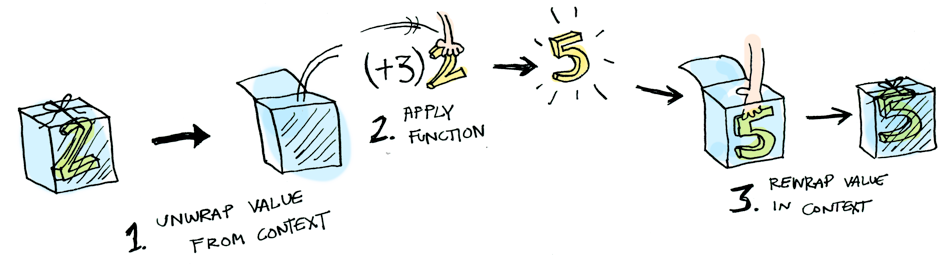
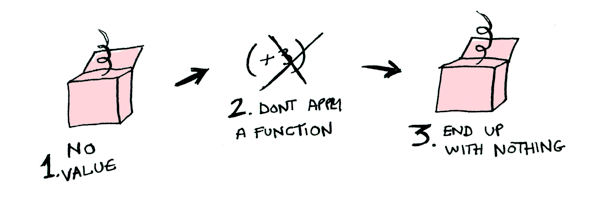
instance Functor Maybe where
    fmap :: (a -> b) -> Maybe a -> Maybe b
    fmap f (Just x) =
    fmap f Nothing  =

instance Functor Maybe where
    fmap :: (a -> b) -> Maybe a -> Maybe b
    fmap f (Just x) = Just (f x)
    fmap _ Nothing  = Nothing

Definitely Maybe

post = Post.find_by_id(1)
if post
  return post.title
else
  return nil
end

findPost     :: PostId -> Maybe Post
getPostTitle :: Post -> Title

firstPostTitle :: Maybe Title
firstPostTitle = fmap getPostTitle (findPost 1)
infixl 4 <$>
(<$>) :: Functor f => (a -> b) -> f a -> f b
(<$>) = fmap

firstPostTitle = getPostTitle <$> findPost 1

The List Functor 

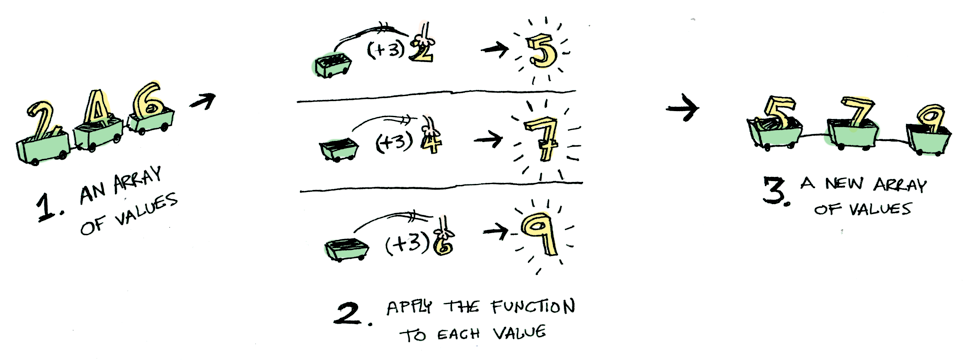
instance Functor [] where
    fmap :: (a -> b) -> [a] -> [b]
    fmap = map
ghci> fmap (*2) [1..3]
[2,4,6]
ghci> map (*2) [1..3]
[2,4,6]
ghci> fmap (*2) []  -- ?

The Arrow Functor 

instance Functor ((->) r) where
    fmap :: (a -> b) -> (r -> a) -> r -> b
    fmap f g =
ghci> :kind (->)
(->) :: Type -> Type -> Type  -- this kind signature is enough for us, 
                              -- albeit it's slightly inaccurate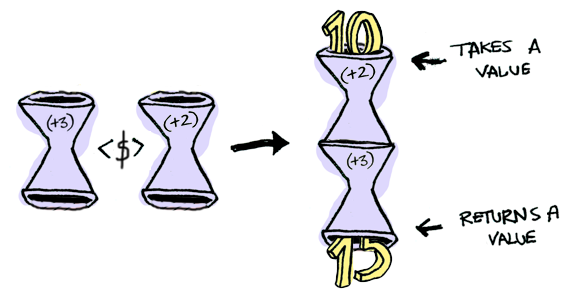
instance Functor ((->) r) where
    fmap :: (a -> b) -> (r -> a) -> r -> b
    fmap = (.)  -- fmap f = \g -> f . g, 
                -- this is known as POST-COMPOSITION in category theory
ghci> let foo = fmap (+3) (+2)
ghci> foo 10
15

ghci> :kind (->) Int
(->) Int :: Type -> Type
f : A \to B \\ C(R, f) : C(R, A) \to C(R, B)

Applicative Functors

Applicative functors 

fmap (*) (Just 3) == Just (3 *)

ghci> let a = fmap (*) [1,2,3,4]
ghci> :t a
a :: [Integer -> Integer]
ghci> fmap (\f -> f 9) a
[9,18,27,36]

Generic way?

class Functor f => Applicative f where  -- f :: Type -> Type
    pure  :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

ghci> :t fmap (++) (Just "hey")
fmap (++) (Just "hey") :: Maybe ([Char] -> [Char])

ghci> :t fmap compare (Just 'a')
fmap compare (Just 'a') :: Maybe (Char -> Ordering)
    liftA2 :: (a -> b -> c) -> f a -> f b -> f c  -- since GHC 8.2.1

What's the point?

Having pure, (<*>), and liftA2 is enough to implement liftAN for fixed values of N!

pure :: a -> f a  -- meaning: we pass a NULLARY function
                  -- i.e., we pass a constant and wrap it in the context
liftA2 :: (a -> b -> c) -> f a -> f b -> f c  -- meaning: we pass a BINARY function

A type f is a Functor if and only if

  1. we can implement fmap : (a -> b) -> (f a -> f b) that accepts a unary function and returns a unary function, and
  2. it is a homomorphism and is subject to its laws.

But what if we wanted to pass N-nary functions of arbitrary arities??

The Maybe Applicative 

instance Applicative Maybe where
    pure :: a -> Maybe a
    pure  =

    (<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
    (<*>) =
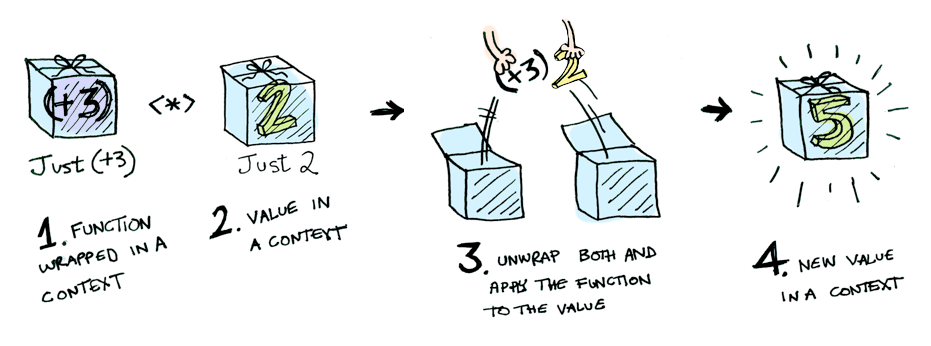
instance Applicative Maybe where
    pure :: a -> Maybe a
    pure = Just
    
    (<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
    Nothing <*> _         = Nothing
    Just f  <*> something = fmap f something
?ghci> pure (++"what") <*> pure "lol"
ghci> Just (+3) <*> Just 9
Just 12
ghci> pure (+3) <*> Just 10
Just 13
ghci> Just (++"hahah") <*> Nothing
Nothing
ghci> pure (++"what") <*> pure "lol"
Just "lolwhat"

The List Applicative 

ghci> [(*2), (+3)] <*> [1, 2, 3]
[2, 4, 6, 4, 5, 6]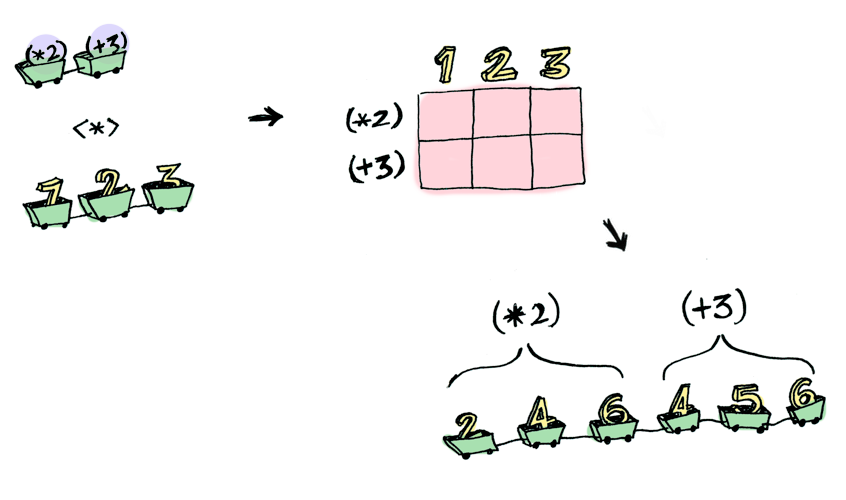
instance Applicative [] where
    pure :: a -> [a]
    pure x    =

    (<*>) :: [a -> b] -> [a] -> [b]
    fs <*> xs =
instance Applicative [] where
    pure :: a -> [a]
    pure x    = [x]

    (<*>) :: [a -> b] -> [a] -> [b]
    fs <*> xs = [f x | f <- fs, x <- xs]
ghci> [ x * y | x <- [2, 5, 10], 
                y <- [8, 10, 11]]
[16, 20, 22, 40, 50, 55, 80, 100, 110]
ghci> (*) <$> [2, 5, 10] <*> [8, 10, 11]
[16, 20, 22, 40, 50, 55, 80, 100, 110]

The Arrow Applicative 

ghci> (pure 3) "blah"
3

instance Applicative ((->) r) where
    pure :: a -> r -> a  -- the K combinator!
    pure x  =
    
    (<*>) :: (r -> a -> b) -> (r -> a) -> r -> b  -- the S combinator!
    f <*> g =

instance Applicative ((->) r) where
    pure :: a -> r -> a  -- the K combinator!
    pure x  = \_ -> x

    (<*>) :: (r -> a -> b) -> (r -> a) -> r -> b  -- the S combinator!
    f <*> g = \x -> f x (g x)
ghci> :t (+) <$> (+3) <*> (*100)
(+) <$> (+3) <*> (*100) :: (Num a) => a -> a
ghci> (+) <$> (+3) <*> (*100) $ 5
508
ghci> (\x y z -> [x,y,z]) <$> (+3) <*> (*2) <*> (/2) $ 5
[8.0,10.0,2.5]

Applicative laws

1. Identity
   pure id <*> v ≡ v

2. Composition
   pure (.) <*> u <*> v <*> w ≡ u <*> (v <*> w)

3. Homomorphism
   pure f <*> pure x ≡ pure (f x)

4. Interchange
   u <*> pure y ≡ pure ($ y) <*> u
   
5. Compatibility w/ Functors
   fmap f u ≡ pure f <*> u

Applicative vs. Functor 

ghci> (*) <$> Just 5 <*> Just 3
Just 15
ghci> liftA2 (*) (Just 5) (Just 3)
Just 15
?ghci> :t liftA3

Apply a function to several arguments?

Pfft, 2ez4konstantine

ghci> (*) <$> Just 5 <*> Just 3
Just 15
ghci> liftA2 (*) (Just 5) (Just 3)
Just 15
ghci> :t liftA3
liftA3 :: Applicative f => (a -> b -> c -> d) -> f a -> f b -> f c -> f d
ghci> import Data.Char (isUpper, isDigit)
ghci> import Control.Applicative (liftA2)
ghci> let isUpperOrDigit = liftA2 (||) isUpper isDigit
ghci> :t isUpperOrDigit 
isUpperOrDigit :: Char -> Bool
ghci> isUpperOrDigit 'A'
True
ghci> isUpperOrDigit '3'
True
ghci> isUpperOrDigit 'a'
False

Applicative style programming

data User = User
    { userFirstName :: String
    , userLastName  :: String
    , userEmail     :: String
    }
type Profile = [(String, String)]

profileExample = 
    [ ("first_name", "Pat"            )
    , ("last_name" , "Brisbin"        )
    , ("email"     , "me@pbrisbin.com")
    ]
lookup "first_name" p :: Maybe String

buildUser :: Profile -> Maybe User
buildUser p = User
    <$> lookup "first_name" p
    <*> lookup "last_name"  p
    <*> lookup "email"      p
-- using liftAN common pattern
buildUser :: Profile -> Maybe User
buildUser p = liftA3 User
                     (lookup "first_name" p)
                     (lookup "last_name"  p)
                     (lookup "email"      p)
-- point-free version
buildUser :: Profile -> Maybe User
buildUser = liftA3 (liftA3 User)
                   (lookup "first_name")
                   (lookup "last_name")
                   (lookup "email")

Alternative

class Applicative f => Alternative f where
    empty :: f a
    (<|>) :: f a -> f a -> f a
instance Alternative Maybe where
    empty :: Maybe a
    empty = Nothing

    (<|>) :: Maybe a -> Maybe a -> Maybe a
    Nothing <|> r = r
    l       <|> _ = l
ghci> Nothing <|> Just 3 <|> empty <|> Just 5
Just 3
instance Alternative [] where
    empty :: [a]
    empty = []
    
    (<|>) :: [a] -> [a] -> [a]
    (<|>) = (++)
ghci> [] <|> [1,2,3] <|> [4]
[1,2,3,4]

Traversable

Doing the same as Foldable but preserving the shape.

class (Functor t, Foldable t) => Traversable t where
    traverse  :: Applicative f => (a -> f b) -> t a -> f (t b)
    sequenceA :: Applicative f => t (f a) -> f (t a)
ghci> let half x = if even x then Just (x `div` 2) else Nothing
ghci> traverse half [2, 4 .. 10]
Just [1, 2, 3, 4, 5]
ghci> traverse half [1 .. 10]
Nothing

instance Traversable Maybe where
    traverse :: Applicative f => (a -> f b) -> Maybe a -> f (Maybe b)
    traverse _ Nothing  =
    traverse f (Just x) =
instance Traversable Maybe where
    traverse :: Applicative f => (a -> f b) -> Maybe a -> f (Maybe b)
    traverse _ Nothing  = pure Nothing
    traverse f (Just x) = Just <$> f x
instance Traversable [] where
    traverse :: Applicative f => (a -> f b) -> [a] -> f [b]
    traverse f = foldr consF (pure [])
      where 
        consF x ys = (:) <$> f x <*> ys
instance Traversable [] where
    traverse :: Applicative f => (a -> f b) -> [a] -> f [b]
    traverse f l =

There exist Bifunctor, Biapplicative, Bifoldable and Bitraversable.

Deriving

If possible, GHC can derive some instances automatically.

{-# LANGUAGE DeriveFunctor     #-}  -- generates `fmap`
{-# LANGUAGE DeriveFoldable    #-}  -- generates `foldr`, `foldMap`, and `null`
{-# LANGUAGE DeriveTraversable #-}  -- generates `traverse`

data Tree a = Leaf | Node a (Tree a) (Tree a)
    deriving (Functor, Foldable, Traversable)

An abundance of typeclasses!

Phantom types

Types really can help!

newtype Hash = MkHash String
class Hashable a where
    hash :: a -> Hash
hashPair :: Int -> Hash
hashPair n = hash (n, n)
hashPair :: Int -> Hash
hashPair n = hash n  -- oops, this is a valid definition!

What can go wrong?

But types can't help you much if you don't use their true power.

Phantom types

newtype Hash a = MkHash String -- `a` is a phantom type, 
                               -- not present in any of the constructors
class Hashable a where
    hash :: a -> Hash a
hashPair :: Int -> Hash (Int, Int)
hashPair n = hash (n, n)
hashPair :: Int -> Hash (Int, Int)
hashPair n = hash n  -- no longer a valid definition!
Hash.hs:7:14: error:
    • Couldn't match type ‘Int’ with ‘(Int, Int)’
      Expected type: Hash (Int, Int)
        Actual type: Hash Int
    • In the expression: hash n
      In an equation for ‘hashPair’: hashPair n = hash n

Limitations of such an approach?

Some real life examples

Crypto

newtype Signature a = Signature ByteString

sign :: Binary t => SecretKey -> t -> Signature t

path package: well-typed paths

data Abs  -- absolute path
data Rel  -- relative path

data Dir  -- directory
data File -- file

newtype Path b t = Path FilePath

-- appending paths
(</>) :: Path b Dir -> Path Rel t -> Path b t

o-clock package: time-safe units

data Second
data Microsecond  -- rough approximation

newtype Time unit = Time (Ratio Natural)

Type extensions

What a wonderful type system

-- v0.0.2: also compiles
prepend2 :: Int -> [Int] -> [Int]
prepend2 x xs = pair ++ xs 
  where pair = [x, x]
-- v0.2.1: doesn't compile!
prepend2 :: a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where pair :: [a]
        pair = [x, x] 
-- v0.0.1: this compiles
prepend2 :: Int -> [Int] -> [Int]
prepend2 x xs = pairFun x ++ xs 
  where pairFun y = [y, y]
-- v0.1.0: compiles or doesn't?
prepend2 :: a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where pair = [x, x]
-- v0.2.0: everything works!
prepend2 :: a -> [a] -> [a]
prepend2 x xs = pairFun x ++ xs 
  where pairFun :: a -> [a]
        pairFun y = [y, y]

Closer look at the error

-- v0.2.1: doesn't compile!
prepend2 :: a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where pair :: [a]
        pair = [x, x] 
Main.hs:7:17: error:
    • Couldn't match expected type ‘a1’ with actual type ‘a’
      ‘a1’ is a rigid type variable bound by
        the type signature for:
          pair :: forall a1. [a1]
        at Main.hs:6:9-19
      ‘a’ is a rigid type variable bound by
        the type signature for:
          prepend2 :: forall a. a -> [a] -> [a]
        at Main.hs:4:1-27
    • In the expression: x
      In the expression: [x, x]
      In an equation for ‘pair’: pair = [x, x]
    • Relevant bindings include
        pair :: [a1] (bound at Main.hs:7:9)
        xs :: [a] (bound at Main.hs:5:12)
        x :: a (bound at Main.hs:5:10)
        prepend2 :: a -> [a] -> [a] (bound at Main.hs:5:1)
  |
7 |         pair = [x, x] 
  | 
(This is compiled with GHC 9.4.8)

We need some scoping

prepend2 :: a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where 
    pair :: [a]
    pair = [x, x] 
id :: a -> a

This definition...

...just contains an implicit forall!

id :: forall a . a -> a

These foralls bind completely different type variables.

prepend2 :: forall a . a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where 
    pair :: forall a . [a]
    pair = [x, x]

Same for the definitions inside the where block!

-- it's basically the same reason as to why THIS doesn't compile
prepend2 :: forall a b . b -> [a] -> [a]
prepend2 x xs = [x, x] ++ xs

-XScopedTypeVariables

{-# LANGUAGE ScopedTypeVariables #-}

-- v1.0.0: COMPILES! Huzzah!
prepend2 :: forall a . a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where 
    pair :: [a]  -- uses same type variable 'a'
    pair = [x, x]

The -XScopedTypeVariables language extension allows to use type variables from a top-level function signature inside this function's body (including the where block). Works only with the forall keyword!

{-# LANGUAGE ScopedTypeVariables #-}

-- v1.0.1: nooo what have you done?! -_-
prepend2 :: a -> [a] -> [a]
prepend2 x xs = pair ++ xs 
  where 
    pair :: [a]  -- throws the SAME error, because the top-level forall is ABSENT
    pair = [x, x]

-XTypeApplications

ghci> read "3"   :: Int
3
ghci> read "3.0" :: Double
3.0
-- in some artifical syntax...
read :: (a :: Type) -> (_ :: String) -> (x :: a)

How many arguments does read have?

read :: forall a . Read a => String -> a
ghci> :t read
read :: Read a => String -> a
ghci> read @Int "3"
3
ghci> read @Double "3.0"
3.0
ghci> :t read @Int
read @Int :: String -> Int
ghci> read "3"   :: Int  -- so, here we basically just pass Int type
3
ghci> read "3.0" :: Double
3.0

-XTypeApplications: visible type application

Now we can pass types as arguments to functions!

This reading list <$> brain

Adit.io: Functors, Applicatives, And Monads In Pictures

LYAH: Chapter 11

Wikibooks/Haskell/Traversable

Applicative style example

StackOverflow: Meaning of Alternative

GHC User Guide: Deriving extensions

Fun with repeated fmap

Monoid (neerc)

Monoid applications

Edward Kmett: All About Monoids

Wikibooks/Haskell/Foldable

Back to square one

newtype First a = First { getFirst :: a }  -- first value
newtype Last  a = Last  { getLast  :: a }  -- last value

How to write mempty for First and Last?

instance Semigroup a => Semigroup (Maybe a) where
    Nothing <> b       = b
    a       <> Nothing = a
    Just a  <> Just b  = Just (a <> b)

instance Semigroup a => Monoid (Maybe a) where
    mempty = Nothing

Maybe creates a FREE Monoid for a given Semigroup :0

Once again, Last and First from the Data.Monoid module differ from the ones in Data.Semigroup:

newtype First a = First { getFirst :: Maybe a }  -- first Just
newtype Last  a = Last  { getLast  :: Maybe a }  -- last Just

The Arrow Monoid 

instance Monoid b => Monoid (a -> b) where
    mempty _ = mempty
    mappend f g x = f x `mappend` g x

Told ya, everything is a Monoid :]

ghci> (flip take [3, 2, 1] <> replicate 2) 1
[3, 1, 1]

But what does it mean? Something like this:

'Tis an interesting Ordering

data Ordering = LT | EQ | GT

instance Monoid Ordering where
    mempty         = EQ
    LT `mappend` _ = LT
    EQ `mappend` y = y
    GT `mappend` _ = GT
module Data.Ord (comparing, ...) where

comparing :: Ord a => (b -> a) -> b -> b -> Ordering
comparing p x y = compare (p x) (p y)

Why do we need such an instance?

data ErrorPosition = ErrorPosition 
    { path   :: String
    , line   :: Int
    , offset :: Int 
    } deriving (Eq)

-- this implementation uses the Monoid instances of (->) and Ordering
instance Ord ErrorPosition where
    compare = comparing path <> comparing line <> comparing offset

For example, to lexicographically sort values of a datatype

Monoids in real life

Composability is what FP for

Vertical scaling vs. Horizontal scaling

1. Combination of plugins is a plugin

2. Combination of configurations is configuration of the same type

3. Combination of event sources is an event source

4. Combination of clusters is a cluster

5. Combination of parsers is a parser

6. Combination of streams is a stream

7. Combination of functions is a function

and so on...

Haskell For All: Scalable program architectures

Partial options monoid pattern

data Options = Options
  { oRetryCount    :: Int
  , oHost          :: String
  , oCharacterCode :: Maybe Char
  } deriving (Show, Eq)

Goal: we want to have options. We want to create multiple versions of records and combine them (defaults + file config + CLI)

Use Monoid! (full details in blog post)

data PartialOptions = PartialOptions
   { poRetryCount    :: Last Int
   , poHost          :: Last String
   , poCharacterCode :: Last (Maybe Char)
   } deriving (Show, Eq)
instance Monoid PartialOptions where
    mempty = PartialOptions mempty mempty mempty
    mappend x y = PartialOptions 
        { poRetryCount    = poRetryCount    x <> poRetryCount    y
        , poHost          = poHost          x <> poHost          y
        , poCharacterCode = poCharacterCode x <> poCharacterCode y
        }

And so on...

fmap fmap fmap fmap fmap

ghci> :t fmap
fmap :: Functor f => (a -> b) -> f a -> f b

ghci> :t fmap fmap
fmap fmap
  :: (Functor f, Functor f1) => f1 (a -> b) -> f1 (f a -> f b)

ghci> :t fmap fmap fmap
fmap fmap fmap
  :: (Functor f, Functor f1) => (a -> b) -> f1 (f a) -> f1 (f b)

ghci> :t fmap fmap fmap fmap
fmap fmap fmap fmap
  :: (Functor f, Functor f1, Functor f2) =>
     f2 (f1 (a -> b)) -> f2 (f1 (f a -> f b))

ghci> :t fmap fmap fmap fmap fmap
fmap fmap fmap fmap fmap
  :: Functor f => (a1 -> b) -> (a -> a1) -> f a -> f b
ghci> let fmap5 = fmap fmap fmap fmap fmap 
ghci> fmap5 (+1) (*2) [1..5]
[3, 5, 7, 9, 11]

-XAllowAmbiguousTypes

-- do you see problems with this code?
class Size a where
    size :: Int
    • Could not deduce (Size a0)
      from the context: Size a
        bound by the type signature for:
                   size :: forall {k} (a :: k). Size a => Int
        at Main.hs:7:3-13
      The type variable ‘a0’ is ambiguous
{-# LANGUAGE AllowAmbiguousTypes #-}

class Size a where size :: Int
instance Size Int    where size = 8
instance Size Double where size = 16

ghci> size  -- this all looks great, but how do I MEANINGFULLY CALL the function?!

    • Ambiguous type variable ‘a0’ arising from a use of ‘size’
      prevents the constraint ‘(Size a0)’ from being solved.
      Probable fix: use a type annotation to specify what ‘a0’ should be.
      Potentially matching instances:
        instance Size Double -- Defined at Main.hs:14:10
        instance Size Int -- Defined at Main.hs:11:10
ghci> size @Double  -- use -XTypeApplications
16
-- simple plain Haskell
class Size a where
    size :: a -> Int
-- this one's better
class Size a where
    size :: Proxy a -> Int
-- data Proxy t = Proxy

The Show Must Go On

-- v0.0.0: this doesn't work IN GENERAL, only works for 'Integer's
incShow :: String -> String
incShow = show . (+1) . read

Result:

ghci> incShow @Int "3"
"4"
ghci> incShow @Double "3.2"
"4.2"
ghci> incShow @Rational "3 % 5"
"8 % 5"
-- v0.0.1: why doesn't THIS work?
incShow :: (Show a, Num a, Read a) => String -> String
incShow = show . (+1) . read
{-# LANGUAGE AllowAmbiguousTypes #-}

-- v0.0.2: why doesn't it STILL work?!
incShow :: (Read a, Show a, Num a) => String -> String
incShow = show . (+1) . read
{-# LANGUAGE AllowAmbiguousTypes #-}
{-# LANGUAGE TypeApplications    #-}

-- v1.0.0: free, at last
incShow :: forall a . (Read a, Show a, Num a) => String -> String
incShow = show . (+1) . read @a
Made with Slides.com