return 5 >>= Lecture

Type helpers

Typed holes

foo :: a -> Int
foo _ = 0

-- same behavior:
foo myUnusedA = 0

_ to the left of = means I don't care about this pattern

_ to the right of = means typed hole

foo :: a -> b
foo x = _

Lecture5.hs:76:9: error:
    • Found hole: _ :: b
      Where: ‘b’ is a rigid type variable bound by
               the type signature for:
                 bar :: forall a b. a -> b
               at Lecture5.hs:75:1-1

Your code will never compile with type hole.

But it's useful to see type of the term to be used instead of hole.

Type wildcards

poid :: Int -> _
poid = show

Lecture5.hs:78:16: error:
    • Found type wildcard ‘_’ standing for ‘String’
      To use the inferred type, enable PartialTypeSignatures
    • In the type signature: poid :: Int -> _
   |
78 | poid :: Int -> _
   |

With PartialTypeSignatures turned off use of wildcards in types is similar to type hole in term.

Monads

Монада - це абстракція лінійного ланцюжка пов'язаних обчислень. Монада дозволяють організовувати послідовні обчислення.

Концепція монади, і термін спочатку походять з теорії категорій, де вона визначається як функтор з додатковою структурою.

Blog example

Imperative style: change value in variable

Functional style: create new variable with new value

data Post = Post { pTitle :: String, pBody :: String }

data Blog = Blog
  { bPosts   :: [Post]
  , bCounter :: Int
  }

readPost :: Int -> Blog -> (Post, Blog)
readPost i blog = (bPosts blog !! i, blog { bCounter = bCounter blog + 1 })

newPost :: Post -> Blog -> Blog
newPost p blog = blog { bPosts = p : bPosts blog }

read12AndNew blog =
  let (post1, blog') = readPost 1 blog
      ((), blog'') = newPost (Post "Bla" "<text>") blog'
      (post2, blog''') = readPost 2 blog''
   in blog'''

What is a Monad?

Variable — container for data.

Monad — container for sequentially composable computation.

Monad is a general way to describe idea of computations where you can combine computations in a such way so that next computation depends on result of previous computation.

Monad type class

class Monad m where   -- m :: * -> *
    return :: a -> m a                  -- return
    (>>=)  :: m a -> (a -> m b) -> m b  -- bind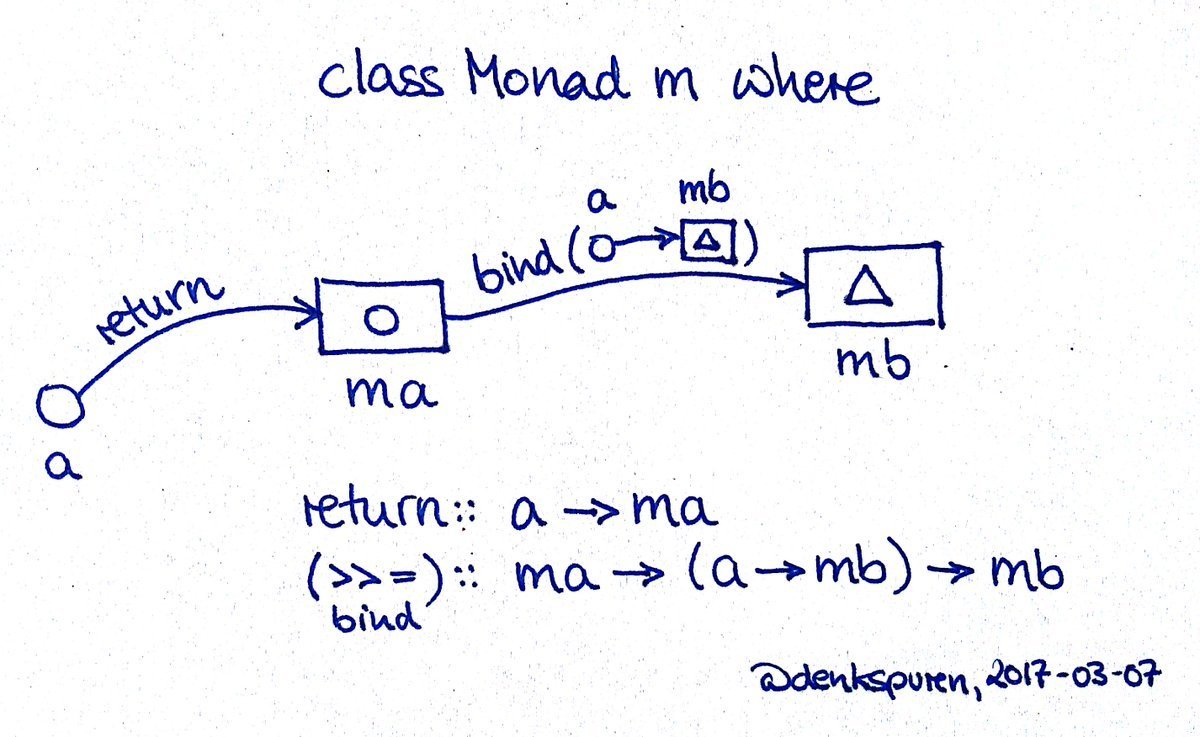

* Image source

Blog example (new version)

newtype BlogM a = BlogM (Blog -> (a, Blog))

readPost' :: Int -> BlogM Post
readPost' i = BlogM (readPost i)

newPost' :: Post -> BlogM ()
newPost' p = BlogM (newPost p)

instance Monad BlogM where
  (BlogT fa) >>= g = BlogM $ \b ->
    let (r, b') = fa b
        BlogM h = g r
     in h b'
  return a = BlogM (\b -> (a, b))

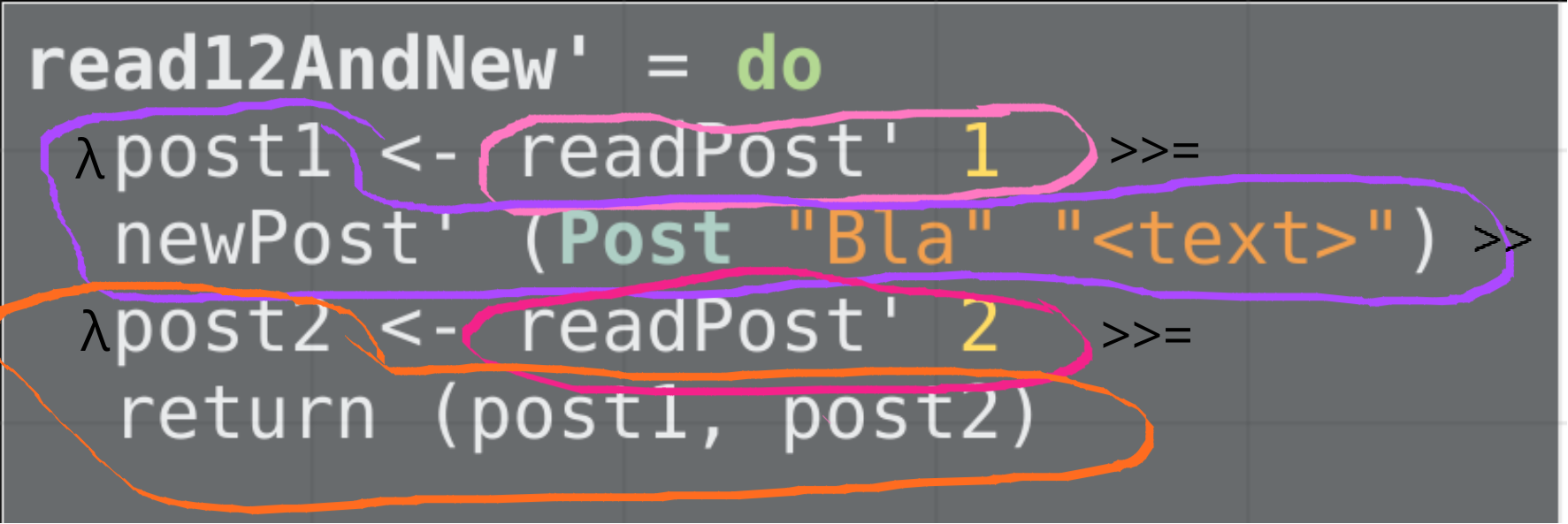
read12AndNew' =
  readPost' 1 >>= \post1 ->
    newPost' (Post "Bla" "<text>") >>= \() ->
    readPost' 2 >>= \post2 ->
      return (post1, post2)

myPost =
  Post "Bla" "<text>"

read12AndNew blog =
  let (post1, blog') =
        readPost 1 blog
      ((), blog'') =
        newPost myPost blog'
      (post2, blog''') =
        readPost 2 blog''
   in blog'''

Compare with previous:

read12AndNew' = do
  post1 <- readPost' 1
  newPost' (Post "Bla" "<text>")
  post2 <- readPost' 2
  return (post1, post2)

Nicer with do syntax:

Monadic blog:

Some tips

instance Monad BlogT where
  (BlogT fa) >>= g = BlogT $ \b ->
    let (r, b') = fa b
        BlogT h = g r in h b'
  return a = BlogT (\b -> (a, b))

instance Functor BlogT where
  fmap = liftM
instance Applicative BlogT where
  pure = return
  (<*>) = ap

Do syntax cheat sheet:

read12AndNew' = do
  post1 <- readPost' 1
  newPost' (Post "Bla" "<text>")
  post2 <- readPost' 2
  return (post1, post2)

Easy way to provide instances:

Functor and Applicative instances are required, but easily defined through Monad.

State monad

newtype State s a = State { runState :: s -> (a, s) }

instance Monad (State s) where
    return :: a -> State s a
    return a = State $ \s -> (a, s)

    (>>=) :: State s a -> (a -> State s b) -> State s b
    oldState >>= f = ...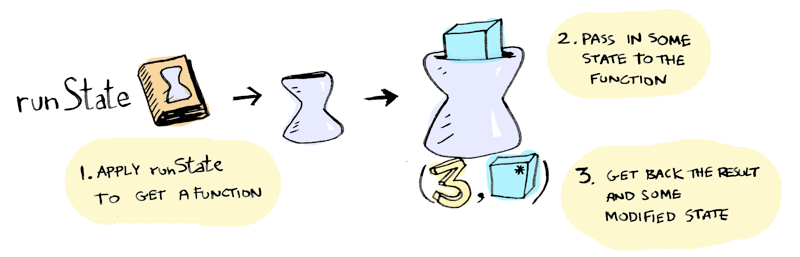

type BlogT a = State Blog a

Blog on State

type BlogS = State Blog

readPostS :: Int -> BlogS Post
readPostS i =
  modify (\b ->
    b { bCounter = bCounter b + 1 }) >>
  gets ((!! i) . bPosts)

newPostS :: Post -> BlogS ()
newPostS p = modify $ \b ->
  b { bPosts = p : bPosts b }

counterS :: BlogS Int
counterS = gets bCounter

Useful functions

get       :: State s s
put       :: s -> State s ()
modify    :: (s -> s) -> State s ()
gets      :: (s -> a) -> State s a
withState :: (s -> s) -> State s a -> State s a
evalState :: State s a -> s -> a
execState :: State s a -> s -> s

read12AndNewS :: State (Post, Post)
read12AndNewS =
  readPostS 1
    >>= \post1 ->
    newPostS (Post "Bla" "<text>") >>
      readPostS 2 >>= \post2 ->
      return (post1, post2)

evalRead12AndNewS
  :: Blog -> (Post, Post)
evalRead12AndNewS =
  evalState read12AndNewS

Repeating monadic action

spamWithPosts :: Int -> State Blog ()
spamWithPosts n = ??
-- post same post N times

Repeat N times?

Control.Monad> :t replicateM
replicateM :: Applicative m => Int -> m a -> m [a]

Control.Monad> :t replicateM_
replicateM_ :: Applicative m => Int -> m a -> m ()

spamWithPosts :: Int -> State Blog ()
spamWithPosts n =
    replicateM_ n (newPostS myPost)

Repeat for each element of a list?

multiNewPost :: [Post] -> State Blog ()
multiNewPost posts = ???

Control.Monad> :t mapM
mapM :: (Traversable t, Monad m) => (a -> m b) -> t a -> m (t b)
Control.Monad> :t mapM_
mapM_ :: (Foldable t, Monad m) => (a -> m b) -> t a -> m ()

multiNewPost :: [Post] -> State Blog ()
multiNewPost = mapM_ newPostS

myPost :: Post
myPost = Post "Spam Title" "Whooo"

More Monads

Immutable context

data Environment = Environment { ids  :: [Int]
                               , name :: Int -> String
                               , near :: Int -> (Int, Int) }

What if function wants to access some global variables, some application managers or services, configured at runtime?

It can't. Pass context to function.

inEnv :: Environment -> Int -> Bool
inEnv env i = i `elem` ids env

anyInEnv :: Environment -> (Int, Int) -> Bool -- we don't use env directly here :(
anyInEnv env (i, j) = inEnv env i || inEnv env j

checkNeighbours :: Environment -> Int -> Maybe String
checkNeighbours env i = if anyInEnv env (near env i)
                        then Just (name env i)
                        else Nothing

But passing context to functions every time explicitly becomes tedious very soon... :(

Reader monad

newtype Reader e a = Reader { runReader :: e -> a }

ask   :: Reader e e                            -- get whole env
asks  :: (e -> a) -> Reader e a                -- get part of env
local :: (e -> b) -> Reader b a -> Reader e a  -- change env locally

instance Monad (Reader e) where
    return :: a -> Reader e a
    return a = Reader $ \_ -> a

    (>>=) :: Reader e a -> (a -> Reader e b) -> Reader e b
    m >>= f = Reader $ \r -> runReader (f $ runReader m r) r

Reader is just wrapper around function which takes some e.

Reader monad instance basically just passes (propagates) immutable environment to each function implicitly (automatically).

Context with Reader

inEnv :: Int -> Reader Environment Bool
inEnv i = asks (elem i . ids)

anyInEnv :: (Int, Int) -> Reader Environment Bool
anyInEnv (i, j) = inEnv i ||^ inEnv j

checkNeighbours :: Int -> Reader Environment (Maybe String)
checkNeighbours i = 
  asks (`near` i) >>= \pair ->
  anyInEnv pair   >>= \res  ->
  if res 
  then Just <$> asks (`name` i)
  else pure Nothing

asks :: (e -> a) -> Reader e a -- get part of env

Believe me, this ^ can be written nicer (in two lines)

ghci> runReader (checkNeighbours 0) $ Environment [1] show (const (1,3))
Just "0"
ghci> runReader (checkNeighbours 0) $ Environment [2] show (const (1,3))
Nothing

Why Reader?

It's not very clear from slides but Reader is the most important monad in real life.

1. You don't need to pass configs and parameters explicitly.

2. You can't accidentally change environment because you don't have direct access to it.

3. Your implementations can be polymorphic and can work with different parts of config.

Better usage example in your Homework.

Maybe monad

data Maybe a = Nothing | Just a

instance Monad Maybe where
    return :: a -> Maybe a
    return = Just
  
    (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
    Nothing >>= _ = Nothing
    Just a  >>= f = f a

Examples

ghci> Just 5 >>= (\x -> Just $ x + 3)
Just 8

ghci> Just 5 >>= (\x -> return $ x + 3)
Just 8

maybePair :: Maybe a -> Maybe b -> Maybe (a, b)    -- naive implementation
maybePair Nothing  _        = Nothing
maybePair _        Nothing  = Nothing
maybePair (Just a) (Just b) = Just (a, b)

ghci> Nothing >>= (\x -> return $ x + 3)
Nothing

ghci> Just 3 >>= \x -> Just 4 >>= \y -> Just (x + y)
Just 7

maybePair :: Maybe a -> Maybe b -> Maybe (a, b)    -- monadic implementation
maybePair ma mb = ma >>= \a -> mb >>= \b -> Just (a, b)

monadPair :: Monad m => m a -> m b -> m (a, b)    -- polymorphic implementation
monadPair ma mb = ma >>= \a -> mb >>= \b -> return (a, b)

Maybe monad in practice

stripUsername :: String -> Maybe String
stripUsername ""          = Nothing
stripUsername name@(n:ns) = case isSpace n || isPunctuation n of
    True  -> stripUsername ns
    False -> Just name

validateLength :: Int -> String -> Maybe String
validateLength maxLen s = if length s > maxLen
                          then Nothing
                          else Just s

Why not?

validateLength :: Int -> String -> Bool
validateLength maxLen s = length s > maxLen

Overcoming boolean blindness with evidence

newtype Username = Username String deriving (Eq, Show)

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = ???

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = case stripUsername name of
    Nothing    -> Nothing
    Just name' -> case validateLength 15 name' of
        Nothing     -> Nothing
        Just name'' -> Just $ Username name''

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= validateLength 15 >>= return . Username

YouTube: Teaching Haskell For Understanding by Julie Moronuki

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= \name' ->

                  case validateLength 15 name' of
        Nothing     -> Nothing
        Just name'' -> Just $ Username name''

mkUser :: String -> Maybe Username  -- FP programming pattern: smart constructor
mkUser name = stripUsername name >>= \name' ->

                       validateLength 15 name' >>= \name'' ->

                       Just $ Username name''

Either monad

data Either e a = Left e | Right a

instance Monad ...

ghci> :kind Either
Either :: * -> * -> *

instance Monad (Either a) where ...  -- Either a :: * -> *

ghci> :kind Either String
Either String :: * -> *
ghci> :kind Either Int
Either Int :: * -> *

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b
    Left e  >>= f = ...
    Right a >>= f = ...

instance Monad (Either e) where ...  -- Either a :: * -> *
    return :: a -> Either e a
    return = Right

    (>>=) :: Either e a -> (a -> Either e b) -> Either e b
    Left e  >>= _ = Left e
    Right a >>= f = f a

Types really can help!

Either monad in practice

data ValidationError = InvalidStrip | TooBigLength

stripUsername :: String -> Either ValidationError String
stripUsername ""          = Left InvalidStrip
stripUsername name@(n:ns) = case isSpace n || isPunctuation n of
    True  -> stripUsername ns
    False -> Right name

validateLength :: Int -> String -> Either ValidationError String
validateLength maxLen s = if length s > maxLen
                          then Left TooBigLength
                          else Right s

mkUser :: String -> Either ValidationError Username
mkUser name = stripUsername name >>= validateLength 15 >>= return . Username

ghci> mkUser "   "
Left InvalidStrip
ghci> mkUser " ...  I Am The Greatest Hero Of All Times ... "
Left TooBigLength
ghci> mkUser "JustDima..."
Right ( Username "JustDima..." )

Monad composition

(.)   ::            (b ->   c) -> (a ->   b) -> a ->   c

(<=<) :: Monad m => (b -> m c) -> (a -> m b) -> a -> m c

m >>= (f >=> g) ≡ m >>= f >>= g
m >>= (f <=< g) ≡ m >>= g >>= f

(f >=> g) >=> h ≡ f >=> (g >=> h)    -- associativity

safeTail :: [a] -> Maybe [a]
safeInit :: [a] -> Maybe [a]

safeStrip :: [a] -> Maybe [a]
safeStrip = safeTail >=> safeInit

(>=>) :: Monad m => (a -> m b) -> (b -> m c) -> a -> m c

stripUsername  :: String -> Maybe String
validateLength :: Int -> String -> Maybe String

mkUser :: String -> Maybe Username
mkUser name = stripUsername name >>= validateLength 15 >>= Just . Username
mkUser      = stripUsername      >=> validateLength 15 >=> Just . Username

Monad zen

(>>) :: Monad m => m a -> m b -> m b  -- then
m >> k = m >>= \_ -> k

ghci> Just 3 >> Just 5
Just 5

ghci> Nothing >> Just 5
Nothing

Why not?

_ >> k = k

ghci> [True,False] >> [1,2,3]
[1,2,3,1,2,3]

-- 'guard' is a polymorphic function but for lists looks like this:
guard :: Bool -> [()]
guard True  = [()]
guard False = []

ghci> [True,False,True] >> [1,2]
[1,2,1,2,1,2]
ghci> [True,False,True] >>= \b -> guard b >> [1,2]
[1,2,1,2]

Monadic myths

1. Monads are impure.

2. Monads are about effects.

3. Monads are about state.

4. Monads are about imperative sequencing.

5. Monads are about IO.

6. Monads are a «back-door» in the language to perform side-effects.

7. Monads are an embedded imperative language inside Haskell.

8. Monads require knowing abstract mathematics.

9. Monads are unique to Haskell.

This presentation is awesome — look through it

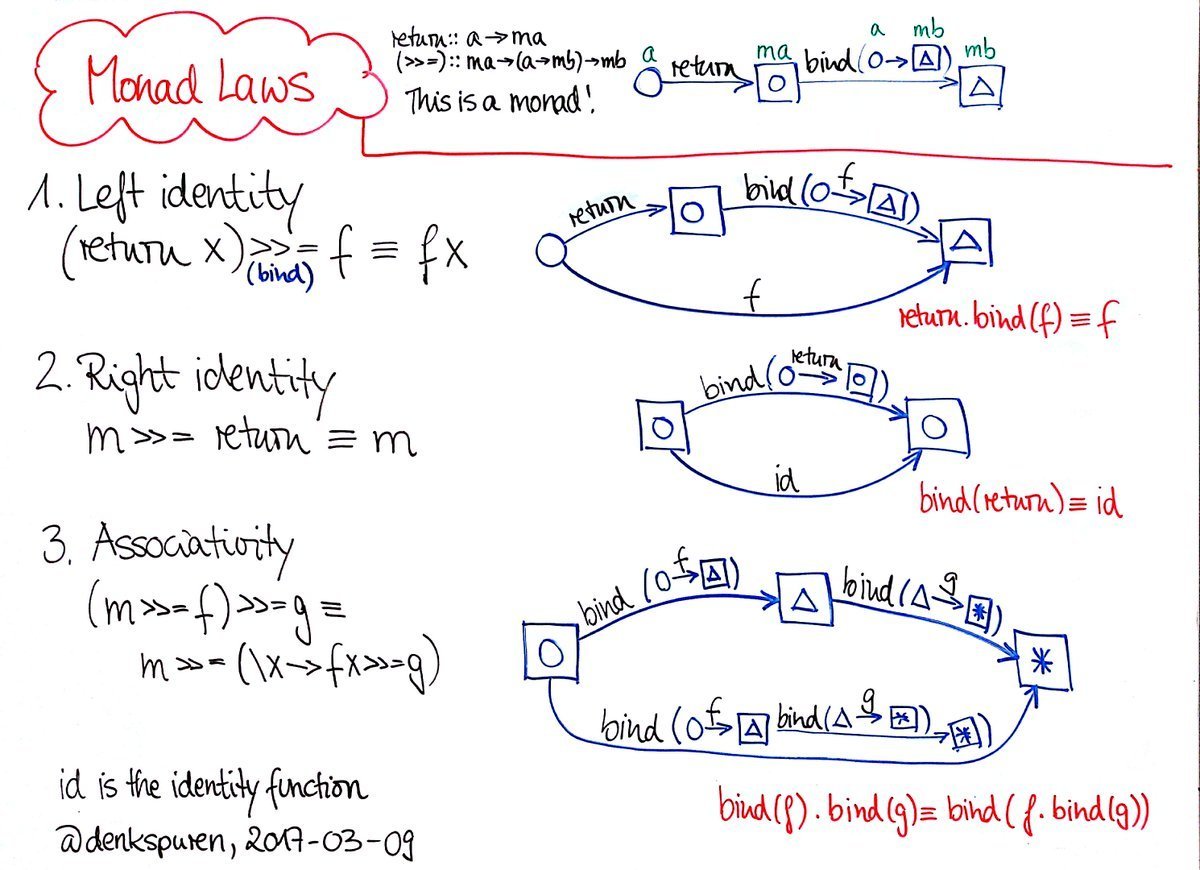
Monad laws

1. return a >>= f  ≡ f a                      -- left identity

2. m >>= return    ≡ m                        -- right identity

3. (m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)  -- associativity

Going deeper in monad

LearnYouAHaskell (chapter 12)

Yet another monad tutorial (ru)

Monads for functional programming (P. Wadler)

Functors, Applicatives and Monads in pictures

HaskellWikiBook: Understanding Monads/Maybe

Read list

(read using Reader monad for understanding)

LearnYouAHaskell (chapter 13)

Three useful monads

The State Monad: A Tutorial for the Confused?

Reader monad with examples

Control.Monad.Reader: simple examples

Typed holes tutorial

hackage: Control.Monad.State

HaskellWikiBook: Understanding State Monad

GHCWiki: PartialTypeSignatures

HaskellWikiBook: Continuation passing style

StackOverflow: How and why does Cont monad work?

HaskellForall: The Continuation Monad

Continuations From the Ground Up