runLecture ::

\Lecture -> (7, Lecture)

Writer Monad

Logging evaluation

binPow :: Int -> Int -> Int
binPow 0 _      = 1
binPow n a
    | even n    = let b = binPow (n `div` 2) a in b * b
    | otherwise = a * binPow (n - 1) a

type IntWithLog = (Int, String)

binPow :: Int -> Int -> IntWithLog
binPow 0 _      = (1, "")
binPow n a
    | even n    = let (b, msg) = binPow (n `div` 2) a 
                  in (b * b, msg ++ "Square " ++ show b ++ "\n")
    | otherwise = let (b, msg) = binPow (n - 1) a
                  in (a * b, msg ++ "Mul " ++ show a ++ " and " ++ show b ++ "\n")

ghci> putStr $ snd $ binPow 3 2
Mul 2 and 1
Square 2
Mul 2 and 4

Lets add some logging to our function

Writer monad

binPow :: Int -> Int -> Writer String Int
binPow 0 _      = return 1
binPow n a
    | even n    = binPow (n `div` 2) a >>= \b -> 
                  tell ("Square " ++ show b ++ "\n") >>
                  return (b * b)
    | otherwise = binPow (n - 1) a >>= \b -> 
                  tell ("Mul " ++ show a ++ " and " ++ show b ++ "\n") >>
                  return (a * b)

newtype Writer w a = Writer { runWriter :: (a, w) } -- a is value, w is log

instance Monoid w => Monad (Writer w) where
    return :: a -> Writer w a
    return a = Writer (a, mempty)
    
    (>>=) :: Writer w a -> (a -> Writer w b) -> Writer w b
    Writer (a, oldLog) >>= f = let Writer (b, newLog) = f a 
                               in Writer (b, oldLog <> newLog)

tell       :: w -> Writer w ()
execWriter :: Writer w a -> w
writer     :: (a, w) -> Writer w a

ghci> putStr $ execWriter $ binPow 3 2
...

binPow :: Int -> Int -> Writer String Int
binPow 0 _      = return 1
binPow n a
    | even n    = binPow (n `div` 2) a >>= \b -> 
                  writer (b * b, "Square " ++ show b ++ "\n")
    | otherwise = binPow (n - 1) a >>= \b -> 
                  writer (a * b, "Mul " ++ show a ++ " and " ++ show b ++ "\n")

Comparison to naive approach

1. Decouple logic and logging

binPow (n `div` 2) a >>= \b -> 
tell ("Square " ++ show b ++ "\n") >>
return (b * b)

2. Concat logs easily

binPow 3 2 >> binPow 3 7

Ecosystem confusion

Such Writer is described in LYAH and its good for simple explanation. But this type doesn't exist in real world libraries.

Writer is special case of more complex type — WriterT, which means...

1. There's no `Writer` constructor. You can't pattern match on it.

2. There's no `Writer` constructor. Use writer function to create.

Moreover... Things are not too friendly for beginners. There're two libraries where you can find Writer: transformers & mtl.

1. transformers: only types and functions

import Control.Monad.Trans.Writer (Writer, writer, ... )

2. mtl: transformers + extra interfaces + shorter imports

import Control.Monad.Writer (Writer, writer, ... )

Just a wrapper

ghci> ([1,2,3], "aba") >> ([5,10], True)
([1,2,3,5,10], True)

There exist instance Monad for pair

instance Monoid a => Monad ((,) a) where
    (u, a) >>= k = case k a of (v, b) -> (u `mappend` v, b)

Basically, Writer is just wrapper around pair. But, please, don't use monad instance for pair. You need to have very good reason for doing this.

When to use Writer?

Never. It's not a joke. Implementation is leaky...

Use writer-cps

Well, there actually exist use cases:

1. Pure logging

2. Collecting intermediate results

Reader Monad

Immutable context

data Environment = Environment { ids  :: [Int]
                               , name :: Int -> String
                               , near :: Int -> (Int, Int) }

What if function wants to access some global variables, some application managers or services, configured at runtime?

It can't. Pass context to function.

inEnv :: Environment -> Int -> Bool
inEnv env i = i `elem` ids env

anyInEnv :: Environment -> (Int, Int) -> Bool -- we don't use env directly here :(
anyInEnv env (i, j) = inEnv env i || inEnv env j

checkNeighbours :: Environment -> Int -> Maybe String
checkNeighbours env i = if anyInEnv env (near env i)
                        then Just (name env i)
                        else Nothing

But passing context to functions every time explicitly becomes tedious very soon... :(

Reader monad

newtype Reader e a = Reader { runReader :: e -> a }

ask   :: Reader e e                            -- get whole env
asks  :: (e -> a) -> Reader e a                -- get part of env
local :: (e -> b) -> Reader b a -> Reader e a  -- change env locally

instance Monad (Reader e) where
    return :: a -> Reader e a
    return a = Reader $ \_ -> a

    (>>=) :: Reader e a -> (a -> Reader e b) -> Reader e b
    m >>= f = Reader $ \r -> runReader (f $ runReader m r) r

Reader is just wrapper around function which takes some e.

Reader monad instance basically just passes (propagates) immutable environment to each function implicitly (automatically).

Context with Reader

inEnv :: Int -> Reader Environment Bool
inEnv i = asks (elem i . ids)

anyInEnv :: (Int, Int) -> Reader Environment Bool
anyInEnv (i, j) = inEnv i ||^ inEnv j

checkNeighbours :: Int -> Reader Environment (Maybe String)
checkNeighbours i = 
  asks (`near` i) >>= \pair ->
  anyInEnv pair   >>= \res  ->
  if res 
  then Just <$> asks (`name` i)
  else pure Nothing

asks :: (e -> a) -> Reader e a -- get part of env

Believe me, this ^ can be written nicer (in two lines)

ghci> runReader (checkNeighbours 0) $ Environment [1] show (const (1,3))
Just "0"
ghci> runReader (checkNeighbours 0) $ Environment [2] show (const (1,3))
Nothing

Why Reader?

It's not very clear from slides but Reader is the most important monad in real life.

1. You don't need to pass configs and parameters explicitly.

2. You can't accidentally change environment because you don't have direct access to it.

3. Your implementations can be polymorphic and can work with different parts of config.

Type helpers

Typed holes

foo :: a -> b
foo x = _

_ to the left of = means I don't care about this pattern

_ to the right of = means typed hole

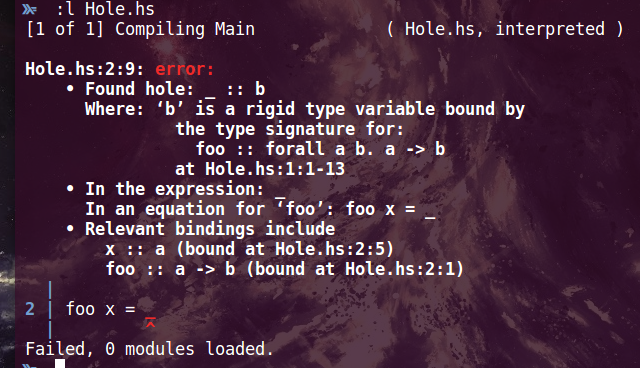
Named hyped holes

mfold :: [Maybe Bool] -> [Either Bool ()]
mfold = foldr _f _z

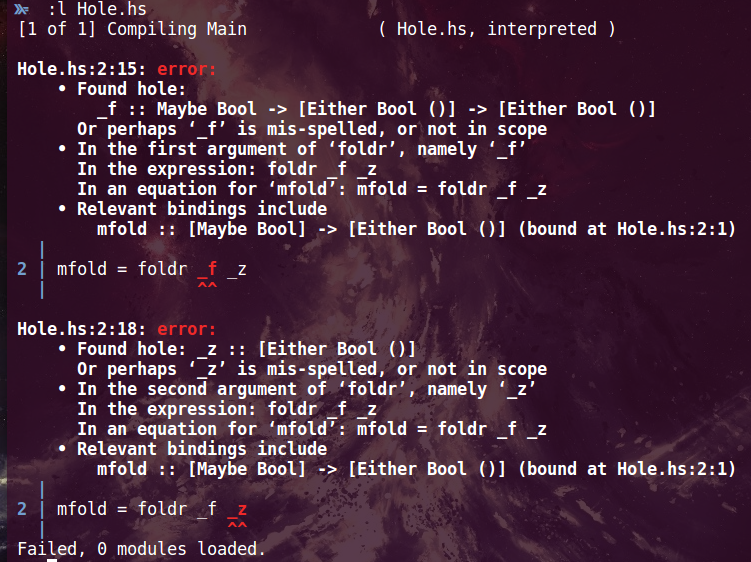
How can I use typed holes?

join :: Monad m => m (m a) -> m a
join m = _

Simple reasoning + types = easy programming

    • Found hole: _ :: m a

What can I do with monad? Only >>= and return. Well, return doesn't help me here obviously, so...

join :: Monad m => m (m a) -> m a
join m = _k >>= _f

    • Found hole: _k :: m a0
    • Found hole: _f :: a0 -> m a

Well, m variable obviously is not a function, so...

join :: Monad m => m (m a) -> m a
join m = m >>= _f

    • Found hole: _f :: m a -> m a

Hmm... Which function takes x and returns x? Oh, wait, I know!

join :: Monad m => m (m a) -> m a
join m = m >>= id

-XPartialTypeSignatures

{-# LANGUAGE PartialTypeSignatures #-}

foo :: _ -> Bool
foo x = not x

Hole.hs:3:8: warning: [-Wpartial-type-signatures]
    • Found type wildcard ‘_’ standing for ‘Bool’
    • In the type signature: foo :: _ -> Bool
  |
3 | foo :: _ -> Bool
  |        ^

arbitCs :: _ => a -> String
arbitCs x = show (succ x) ++ show (x == x)

Hole.hs:6:12: warning: [-Wpartial-type-signatures]
    • Found type wildcard ‘_’ standing for ‘(Eq a, Enum a, Show a)’
      Where: ‘a’ is a rigid type variable bound by
               the inferred type of
               arbitCs :: (Eq a, Enum a, Show a) => a -> String
               at Hole.hs:7:1-42
    • In the type signature: arbitCs :: _ => a -> String
  |
6 | arbitCs :: _ => a -> String
  |            ^

You can do the same w/o PartialTypeSignatures but compilation fails

State Monad

Evaluation modifies state

Imperative style: change value in variable

Functional style: create new variable with new value

type Stack = [Int]

pop  :: Stack -> ?
push :: Int -> Stack -> ?

type Stack = [Int]

pop  :: Stack -> (Int, Stack)
push :: Int -> Stack -> Stack

pop  :: Stack -> (Int, Stack)
pop (x:xs) = (x, xs)

push :: Int -> Stack -> Stack
push x s = x:s

stackOps :: Stack -> (Int, Stack)
stackOps s = let (x, xs) = pop s
                 s'      = push 5 xs
                 res     = push 10 s'
             in (x, res)

ghci> stackOps [1,2,3]
(1,[10,5,2,3])

State monad

newtype State s a = State { runState :: s -> (a, s) }

instance Monad (State s) where
    return :: a -> State s a
    return a = State $ \s -> (a, s)

    (>>=) :: State s a -> (a -> State s b) -> State s b
    oldState >>= f = ...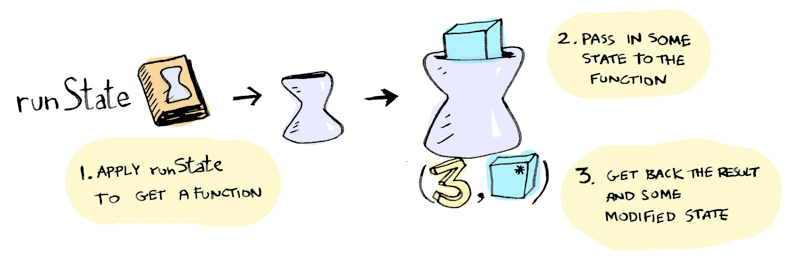

type State s a = s -> (a, s)

State monad explanation

Haskell is purely functional: a function, on the same input, always returns the same output. In other words, a pure function cannot store internal state. However, many algorithms are quite naturally expressed in a stateful way, e.g., quicksort; how can we implement them in Haskell? A simple way to represent a stateful computation is as a pure function that takes the initial state as an argument and returns the result together with the final state. The State type describes such functions:

The fact that State s is a monad means that it implements a certain interface (which is the Monad type class in Haskell, but you can translate that in any language with higher-order functions). Without going into the details of it, the consequence is that we can write stateful functions in an imperative style even in a purely functional language.

/r/haskell: This explanation source

oldState >>= f = State $ \s -> _

    • Found hole ‘_’ with type: (b, s)

oldState >>= f = State $ \s -> let (a, newState) = runState oldState s 
                               in _

    • Found hole ‘_’ with type: (b, s)

(>>=) :: State s a        ->
         (a -> State s b) ->
         State s b

(>>=) :: (s -> (a, s))      ->
         (a -> s -> (b, s)) ->
         (s -> (b, s))

oldState >>= f = State $ \s -> let (a, newState) = runState oldState s 
                               in _k (f a)

    • Found hole ‘_k’ with type: State s b -> (b, s)

instance Monad (State s) where
    return a       = State $ \s -> (a, s)
    oldState >>= f = State $ \s -> let (a, newState) = runState oldState s
                                   in runState (f a) newState

oldState >>= f = State $ \s -> let (a, newState) = runState oldState s 
                               in f a

    • Couldn't match expected type `(b, s)` with actual type `State s b`

Step by step monad instance

Stack on State

type Stack = [Int]

pop :: State Stack Int
pop = state $ \(x:xs) -> (x, xs)

push :: Int -> State Stack ()
push x = ...

stackOps :: State Stack Int
stackOps = pop >>= \x -> push 5 >> push 10 >> return x

Useful functions

get       :: State s s
put       :: s -> State s ()
modify    :: (s -> s) -> State s ()
gets      :: (s -> a) -> State s a
withState :: (s -> s) -> State s a -> State s a
evalState :: State s a -> s -> a
execState :: State s a -> s -> s

gchi> evalState stackOps [1, 2, 3]
1

ghci> execState stackOps [1, 2, 3]
[10,5,2,3]

type Stack = [Int]

pop :: State Stack Int
pop = state $ \(x:xs) -> (x, xs)

push :: Int -> State Stack ()
push x = state $ \xs -> ((), x:xs)

Repeating monadic action

multipop :: Int -> State Stack [Int]
multipop n = ???

Repeat N times?

ghci> :t replicateM
replicateM :: Monad m => Int -> m a -> m [a]

multipop :: Int -> State Stack [Int]
multipop n = replicateM n pop

ghci> runState (multipop 3) [1..10]
([1,2,3], [4,5,6,7,8,9,10])

pop :: State Stack Int
pop = state $ \(x:xs) -> (x, xs)

Repeat for each element of a list?

data StackOperation = Pop | Push Int

doOperations :: [StackOperation] -> State Stack ()
doOperations ops = ???

ghci> :t forM_
forM_ :: (Monad m, Foldable t) => t a -> (a -> m b) -> m ()

doOperations :: [StackOperation] -> State Stack ()
doOperations ops = forM_ ops $ \case  -- -XLambdaCase extension
    Pop    -> pop >> return ()
    Push n -> push n

ghci> execState (doOperations [Pop, Pop, Push 100]) [1..5]
[100,3,4,5]

Cont Monad

Continuation Passing Style (CPS)

function add(a, b) {
    return a + b;
}

add :: Int -> Int -> Int
add x y = x + y

addCPS :: Int -> Int -> (Int -> r) -> r
addCPS x y onDone = onDone (x + y)

function addCPS(a, b, callback) {
    callback(a + b);
}

addCPS(1, 2, function (result) {
    // use result here
});

onInput :: (String -> IO ()) -> IO ()  -- every callback framework
onInput action = forever $ getLine >>= action

JavaScript

Haskell

«Abuse of the Continuation monad can produce code that is impossible to understand and maintain.»

Example (anonymous callbacks)

square :: Int -> Int
square x = x * x

pythagoras :: Int -> Int -> Int
pythagoras x y = (+) (square x) (square y)

addCPS :: Int -> Int -> ((Int -> r) -> r)
addCPS x y = \k -> k (x + y)

squareCPS :: Int -> ((Int -> r) -> r)
squareCPS x = \k -> k (square x)

pythagorasCPS :: Int -> Int -> ((Int -> r) -> r)
pythagorasCPS x y = \k ->  -- k :: Int -> r
    squareCPS x  $ \x2 ->
    squareCPS y  $ \y2 ->
    addCPS x2 y2 $ k       -- addCPS x2 y2 :: (Int -> r) -> r

ghci> pythagorasCPS 3 4 id
25

Cont data type

ghci> :t ($)
($) :: (a -> b) -> a -> b

gchi> :t ($ 2)
($ 2) :: Num a => (a -> b) -> b

ghci> map ($ 2) [(3*), (2+),(1-)]
[6,4,-1]

newtype Cont r a = Cont { runCont :: (a -> r) -> r }

ghci> :t cont
cont :: ((a -> r) -> r) -> Cont r a

gchi> runCont (cont ($ 2)) `map` [(3*), (2+), (1-)]
[6,4,-1]

ghci> runCont (cont ($ 2)) id
2

Example (plain Cont data type)

addCPS :: Int -> Int -> Cont r Int
addCPS x y = cont $ \k -> k (x + y)

squareCPS :: Int -> Cont r Int
squareCPS x = cont $ \k -> k (square x)

pythagorasCPS :: Int -> Int -> Cont r Int
pythagorasCPS x y = cont   $ \k  ->
    runCont (squareCPS x)  $ \x2 ->
    runCont (squareCPS y)  $ \y2 ->
    runCont (addCPS x2 y2) $ k

ghci> runCont (pythagorasCPS 3 4) id
25

Cont monad

newtype Cont r a = Cont { runCont :: (a -> r) -> r }

instance Monad (Cont r) where
    return :: a -> Cont r a
    return a =
    
    (>>=) :: Cont r a -> (a -> Cont r b) -> Cont r b
    Cont arr >>= f =

instance Monad (Cont r) where
    return :: a -> Cont r a
    return a = Cont ($ a)

    (>>=) :: Cont r a -> (a -> Cont r b) -> Cont r b
    Cont arr >>= f = Cont $ \br -> arr $ \a -> runCont (f a) br

    -- arr :: (a -> r) -> r
    -- br  :: (b -> r)
    -- f   :: a -> Cont r b

Example (Cont monad)

addCPS :: Int -> Int -> Cont r Int
addCPS x y = return $ x + y

squareCPS :: Int -> Cont r Int
squareCPS = return . square

pythagorasCPS :: Int -> Int -> Cont r Int
pythagorasCPS x y = squareCPS x >>= \x2 ->
                    squareCPS y >>= \y2 ->
                    addCPS x2 y2

CPS advantages

Good for:

1. Representation of program in compiler

2. Building coroutines

3. Introducing callbacks

4. Tail-recursive optimizations

5. Exception handling

6. Performance optimizations

MonadCont

class Monad m => MonadCont m where
    callCC :: ((a -> m b) -> m a) -> m a  -- call-with-current-continuation

instance MonadCont (Cont r) where
    callCC :: ((a -> Cont r b) -> Cont r a) -> Cont r a
    callCC f = cont $ \c -> runCont (f (\x -> cont $ \_ -> c x)) c

foo :: Int -> Cont r String
foo x = callCC $ \earlyReturn ->
    let y = x ^ 2 + 3 in
    when (y > 20) (earlyReturn "over twenty") >>
    return $ show (y - 4)

callCC gives us back explicit control of continuations

gchi> runCont (foo 2) putStrLn
3

ghci> runCont (foo 10) putStrLn
over twenty

Read list

(read using Reader monad for understanding)

LearnYouAHaskell (chapter 13)

Three useful monads

The State Monad: A Tutorial for the Confused?

Reader monad with examples

Control.Monad.Reader: simple examples

Typed holes tutorial

hackage: Control.Monad.State

HaskellWikiBook: Understanding State Monad

GHCWiki: PartialTypeSignatures

HaskellWikiBook: Continuation passing style

StackOverflow: How and why does Cont monad work?

HaskellForall: The Continuation Monad

Continuations From the Ground Up

Useful Writer trick

import Control.Monad.Writer (Writer, execWriter, tell)

listTellExample :: Writer [Int] ()
listTellExample = tell [1] >> tell [2] >> tell [3]

ghci> execWriter listTellExample
[1,2,3]

output :: a -> Writer [a] ()
output a = tell [a]

listOutputExample :: Writer [Int] ()
listOutputExample = output 1 >> output 2 >> output 3

ghci> execWriter listOutputExample
[1,2,3]