Lecture → (7.5, Lecture)

Parser combinators

What is parsing?

Parsing is the process of converting poorly structured data (e.g. text, bytes) into strongly structured data (e.g. abstract syntax trees w/ meta information, custom data types, etc.).

How do people usually employ parsing?

1. Somehow

2. With parser generators: ANTLR, Yacc/Bison, Happy

3. With parser combinators (for example, the Haskell-written ones)

Idea of parser combinators

We want to combine parsers easily.

We want to build bigger parsers from smaller ones.

Type of parser

What is a type of function which parses integer number?

parseInteger :: String -> Bool

No. We want to get actual Integer.

parseInteger :: String -> Integer

No. Parsers can fail.

parseInteger :: String -> Maybe Integer -- Either for more descriptive error

Now. How do you parse two integers separated by space? Or by any number of spaces? Or comma-separated list of integers? Or the same list inside square brackets [] with any number of spaces between elements?

parseInteger :: String -> Maybe (Integer, String)

Solution

What is the type of a parser?

What is the type of a function that parses integers?

parseInteger :: String -> Bool

No, we want to retrieve an actual Integer. This looks like a predicate.

parseInteger :: String -> Integer

No, parsers can fail.

parseInteger :: String -> Maybe Integer -- 'Either' for a more descriptive error

Close. How do you parse two space-separated integers? Or by any number of spaces? Or a comma-separated list of integers? Or the same list inside the square brackets "[]" with any number of spaces between the elements?

parseInteger :: String -> Maybe (Integer, String)

Solution

Understanding the Parser type

               ┌─ result type         ┌── input stream  ┌─ remaining stream
               │                      │                 │
newtype Parser a = Parser { runP :: String -> Maybe (a, String) }
                             │                │      │
                             └─ selector      │      └─ parsed result
                                              │
                                              └─ parsing may fail

parseInteger :: String -> Maybe (Integer, String)

Instead of this...

... it is more convenient to work with a newtype wrapper

newtype allows us to have useful instances!

Some examples

parseInteger :: Parser Integer  -- String -> Maybe (Integer, String)

Recall the datatype

newtype Parser a = Parser { runP :: String -> Maybe (a, String) }

Specialization to Integers:

runP :: Parser a -> String -> Maybe (a, String)

How to use it and what behavior do we desire?

ghci> runP parseInteger "5"
Just (5, "") :: Maybe (Integer, String)

ghci> runP parseInteger "42x7"
Just (42, "x7") :: Maybe (Integer, String)

ghci> runP parseInteger "abc"
Nothing :: Maybe (Integer, String)

Such behavior allows us to combine parsers relatively easily!

The idea and the first step

The key idea of parser combinators: manually implement simple parsers, implement combinators that combine such parsers, and then build more complex parsers by combining simpler ones via parser combinators.

instance Functor     Parser  -- replace the parser value
instance Applicative Parser  -- run parsers sequentially, one after another
instance Monad       Parser  -- same as above, but with monadic capabilities
instance Alternative Parser  -- allows to choose a non-failing parser

Haskell provides some combinators through standard typeclasses and the underlying functions, which turn out to be convenient to use. What we need are

these four instances!

Simple parsers

newtype Parser a = Parser { runP :: String -> Maybe (a, String) }

-- always succeeds without processing any input
ok :: Parser ()
ok = Parser $ \s -> Just ((), s)

-- fails w/o processing any input if the given parser succeeds, succeeds otherwise
isNot :: Parser a -> Parser ()
isNot parser = Parser $ \s -> case runP parser s of
    Just _  -> Nothing
    Nothing -> Just ((), s)

-- succeeds only if the input stream is empty
eof :: Parser ()
eof = Parser $ \s -> case s of
    [] -> Just ((), "")
    _  -> Nothing

-- processes only the first character, if present, 
-- and returns it if the predicate on this character is true
satisfy :: (Char -> Bool) -> Parser Char
satisfy p = Parser $ \s -> case s of
    []     -> Nothing
    (x:xs) -> if p x then Just (x, xs) else Nothing

Combining simple parsers

-- processes a given character and returns it
char :: Char -> Parser Char
char c = satisfy (== c)

-- always fails without processing any input
notOk :: Parser ()
notOk = isNot ok

ghci> runP eof ""
Just ((),"")
ghci> runP eof "aba"
Nothing
ghci> runP (char 'a') "aba"
Just ('a',"ba")
ghci> runP (char 'x') "aba"
Nothing

-- processes any character / any digit respectively
anyChar, digit :: Parser Char
anyChar = satisfy (const True)
digit   = satisfy isDigit

Instances for more power

instance Functor Parser where
    fmap :: (a -> b) -> Parser a -> Parser b
    fmap f (Parser parser) = Parser (fmap (first f) . parser)

newtype Parser a = Parser { runP :: String -> Maybe (a, String) }

instance Applicative Parser where
    pure :: a -> Parser a
    pure a = Parser $ \s -> Just (a, s)

    (<*>) :: Parser (a -> b) -> Parser a -> Parser b
    Parser pf <*> Parser pa = Parser $ \s -> case pf s of
        Nothing     -> Nothing
        Just (f, t) -> case pa t of
            Nothing     -> Nothing
            Just (a, r) -> Just (f a, r)

    -- can be written more eloquently by using Maybe as a Monad

instance Monad Parser  -- exercise

instance Alternative Parser where  -- exercise
    empty :: Parser a  -- always fails
    (<|>) :: Parser a -> Parser a -> Parser a  -- runs the first parser; 
                                               -- if fails, runs the second parser

Simple combinators: the core

-- datatype
newtype Parser a = Parser { runP :: String -> Maybe (a, String) }

-- simple parsers
eof, ok :: Parser ()
satisfy :: (Char -> Bool) -> Parser Char
empty   :: Parser a

-- parser combinators
fmap  :: (a -> b) -> Parser a -> Parser b
pure  :: a -> Parser a
(<*>) :: Parser (a -> b) -> Parser a -> Parser b  -- apply
(<|>) :: Parser a -> Parser a -> Parser a         -- orElse
(>>=) :: Parser a -> (a -> Parser b) -> Parser b  -- andThen

Simple combinators: cont.

-- datatype
newtype Parser a = Parser { runP :: String -> Maybe (a, String) }

-- simple parsers
eof, ok :: Parser ()
satisfy :: (Char -> Bool) -> Parser Char

-- parser combinators
-- * Functor
fmap  :: (a -> b) -> Parser a -> Parser b
(<$)  :: a -> Parser b -> Parser a  -- replaces the value with the first argument

-- * Applicative
pure  :: a -> Parser a
(<*>) :: Parser (a -> b) -> Parser a -> Parser b
(<*)  :: Parser a -> Parser b -> Parser a  -- sequential comp., result of the 1st
(*>)  :: Parser a -> Parser b -> Parser b  -- sequential comp., result of the 2nd

-- * Alternative
empty :: Parser a
(<|>) :: Parser a -> Parser a -> Parser a  -- orElse
many  :: Parser a -> Parser [a]  -- zero or more
some  :: Parser a -> Parser [a]  -- one or more (should result in a 'NonEmpty') 

-- * Monad
(>>=) :: Parser a -> (a -> Parser b) -> Parser b  -- andThen

Combinator examples

ghci> runP (ord <$> char 'A') "A"
Just (65,"")

ghci> runP ((\x y -> [x, y]) <$> char 'a' <*> char 'b') "abc"
Just ("ab","c")
ghci> runP ((\x y -> [x, y]) <$> char 'a' <*> char 'b') "xxx"
Nothing

ghci> runP (char 'a' <* eof) "a"
Just ('a',"")
ghci> runP (char 'a' <* eof) "ab"
Nothing

ghci> runP (many $ char 'a') "aaabcd"
Just ("aaa","bcd")
ghci> runP (many $ char 'a') "xxx"
Just ("","xxx")
ghci> runP (some $ char 'a') "xxx"
Nothing

ghci> runP (char 'a' <|> char 'b') "abc"
Just ('a',"bc")
ghci> runP (char 'a' <|> char 'b') "bca"
Just ('b',"ca")
ghci> runP (char 'a' <|> char 'b') "cab"
Nothing

More complex combinators

string :: String -> Parser String  -- like 'char' but for Strings
oneOf  :: [String] -> Parser String  -- parses the first matched string

Problem: parse a user's [y/n] answer

data Answer = Yes | No

yesP :: Parser Answer
yesP = Yes <$ oneOf ["y", "Y", "yes", "Yes", "ys"]

noP :: Parser Answer
noP = No <$ oneOf ["n", "N", "no", "No"]

answerP :: Parser Answer
answerP = yesP <|> noP

Parser combinator libraries

-- | @'ParsecT' e s m a@ is a parser with custom data component of error
-- @e@, stream type @s@, underlying monad @m@ and return type @a@.
newtype ParsecT e s m a = ParsecT
  { unParser ::
      forall b.
      State s e ->
      (a -> State s e -> Hints (Token s) -> m b) -> -- consumed-OK
      (ParseError s e -> State s e -> m b) -> -- consumed-error
      (a -> State s e -> Hints (Token s) -> m b) -> -- empty-OK
      (ParseError s e -> State s e -> m b) -> -- empty-error
      m b
  }
-- snippet taken from the Text.Megaparsec.Internal.ParsecT datatype

parsec — the first mature library, very old

attoparsec — fast, poor error messages, backtracks by default

megaparsec — excellent error messages, mature

Types in mature libraries are scary...

Testing

Testing libraries

hspec — declarative unit testing

hedgehog — property-based testing

tasty — testing framework for combining different approaches

• tasty-hspec — tasty provider for hspec

• tasty-hedgehog — tasty provider for hedgehog

It's easier to understand and write things if you're familiar with the IO monad and do-notation but bear with me...

Unit testing

HSpec library (1 / 2)

Test.Unit module

module Test.Unit
       ( hspecTestTree
       ) where

import Data.Maybe (isJust, isNothing)

import Test.Tasty (TestTree)
import Test.Tasty.Hspec (Spec, describe, it, shouldBe, shouldSatisfy, testSpec)

import Parser (char, eof, runP)

hspecTestTree :: IO TestTree
hspecTestTree = testSpec "Simple parser" spec_Parser

spec_Parser :: Spec
spec_Parser = do
  describe "eof works" $ do
    it "eof on an empty input" $
      runP eof "" `shouldSatisfy` isJust
    it "eof on a non-empty input" $
      runP eof "x" `shouldSatisfy` isNothing
  describe "char works" $ do
    it "char parses a character" $
      runP (char 'a') "abc" `shouldBe` Just ('x', "bc")

HSpec library (2 / 2)

Now using our TestTree

module Main where

import Test.Tasty (defaultMain, testGroup)

import Test.Unit (hspecTestTree)

main :: IO ()
main = hspecTestTree >>= \unitTests ->
       let allTests = testGroup "Parser" [unitTests]
       in defaultMain allTests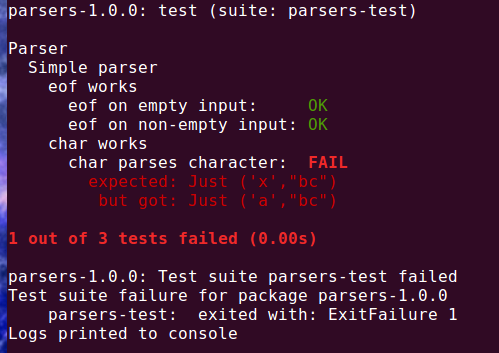

Property-based testing

Shalyto

Writing unit tests for different cases is really boring and tedious. We have a lot of functions, some of which may have corner cases, and our tests will be quite limited in terms of the size of the test set.

With property-based testing:

1. Library generates arbitrary input for your function.

2. Instead of specifying expected values you specify desired properties to which function results should satisfy.

Often it's much more difficult to write property-based tests rather than unit tests. But properties test your functions better (more cases, more reliable, more robust).

Simple example

\forall xs: reverse\ (reverse\ xs)\ \equiv \ xs

import Hedgehog

import qualified Data.List as List
import qualified Hedgehog.Gen as Gen
import qualified Hedgehog.Range as Range

genIntList :: Gen [Int]
genIntList =
  let listLength = Range.linear 0 100000
  in  Gen.list listLength Gen.enumBounded

prop_reverse :: Property
prop_reverse = property $
  forAll genIntList >>= \xs ->
  List.reverse (List.reverse xs) === xs

Shrinking (1 / 3)

If a test is not passed we can show the generated test case. But because this test case is generated randomly, it can be very big! It's much easier to test on smaller inputs.

Property-based libraries usually come with shrinking — a technique for automatically decreasing the size of a faulty test in order to come up with a minimal reproducible example.

Shrinking (2 / 3)

-- drops an element somewhere around the middle of the list
fauxReverse :: [a] -> [a]
fauxReverse xs =
  let sx = List.reverse xs
      mp = length xs `div` 2
      (as, bs) = List.splitAt mp sx
  in as ++ List.drop 1 bs

Let's implement a bad reverse function

prop_fauxReverse :: Property
prop_fauxReverse = property $
    forAll genIntList >>= \xs ->
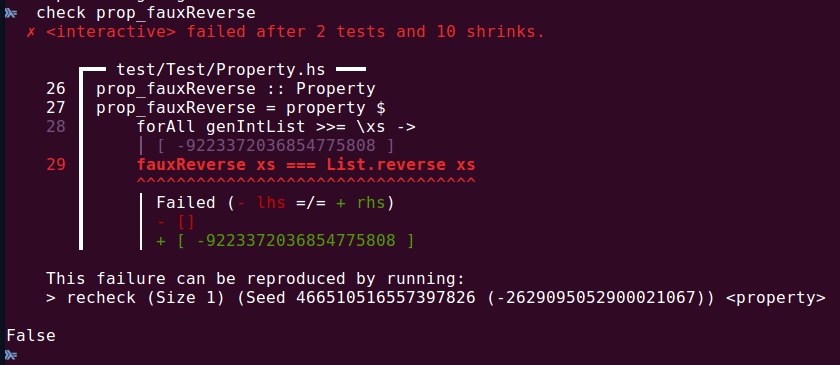
    fauxReverse xs === List.reverse xs

Shrinking (3 / 3)

And the output is...

Some standard use cases

1. Round-trip properties

read        . show      ≡ id
decode      . encode    ≡ id
deserialize . serialize ≡ id

2. Type classes laws

(a <> b) <> c ≡ a <> (b <> c)
a <> mempty ≡ a
mempty <> a ≡ a

Though, some laws are harder to test...

(m >>= f) >>= g ≡ m >>= (\x -> f x >>= g)

You need to generate arbitrary functions and show them. Don't worry, it is possible, just not out of the box...

Testing parsers with properties

Very simple and naive test...

module Test.Property (okTestTree) where

import Hedgehog (Gen, Property, forAll, property, (===))
import Test.Tasty (TestTree)
import Test.Tasty.Hedgehog (testProperty)

import Parser (ok, runP)

import qualified Hedgehog.Gen as Gen
import qualified Hedgehog.Range as Range

okTestTree :: TestTree
okTestTree = testProperty "ok always succeeds" prop_Ok

genString :: Gen String
genString =
  let listLength = Range.linear 0 100
  in  Gen.list listLength Gen.alpha

prop_Ok :: Property
prop_Ok = property $
  forAll genString >>= \s ->
  runP ok s === Just ((), s)

Cont Monad

Continuation Passing Style (CPS)

function add(a, b) {
    return a + b;
}

add :: Int -> Int -> Int
add x y = x + y

addCPS :: Int -> Int -> (Int -> r) -> r
addCPS x y onDone = onDone (x + y)

function addCPS(a, b, callback) {
    callback(a + b);
}

addCPS(1, 2, function (result) {
    // use result here
});

onInput :: (String -> IO ()) -> IO ()  -- every callback framework
onInput action = forever $ getLine >>= action

JavaScript

Haskell

«Abuse of the Continuation monad can produce code that is impossible to understand and maintain.»

Example (anonymous callbacks)

square :: Int -> Int
square x = x * x

pythagoras :: Int -> Int -> Int
pythagoras x y = (+) (square x) (square y)

addCPS :: Int -> Int -> ((Int -> r) -> r)
addCPS x y = \k -> k (x + y)

squareCPS :: Int -> ((Int -> r) -> r)
squareCPS x = \k -> k (square x)

pythagorasCPS :: Int -> Int -> ((Int -> r) -> r)
pythagorasCPS x y = \k ->  -- k :: Int -> r
    squareCPS x  $ \x2 ->
    squareCPS y  $ \y2 ->
    addCPS x2 y2 $ k       -- addCPS x2 y2 :: (Int -> r) -> r

ghci> pythagorasCPS 3 4 id
25

Cont data type

ghci> :t ($)
($) :: (a -> b) -> a -> b

gchi> :t ($ 2)
($ 2) :: Num a => (a -> b) -> b

ghci> map ($ 2) [(3*), (2+),(1-)]
[6,4,-1]

newtype Cont r a = Cont { runCont :: (a -> r) -> r }

ghci> :t cont
cont :: ((a -> r) -> r) -> Cont r a

gchi> runCont (cont ($ 2)) `map` [(3*), (2+), (1-)]
[6,4,-1]

ghci> runCont (cont ($ 2)) id
2

Example (plain Cont data type)

addCPS :: Int -> Int -> Cont r Int
addCPS x y = cont $ \k -> k (x + y)

squareCPS :: Int -> Cont r Int
squareCPS x = cont $ \k -> k (square x)

pythagorasCPS :: Int -> Int -> Cont r Int
pythagorasCPS x y = cont   $ \k  ->
    runCont (squareCPS x)  $ \x2 ->
    runCont (squareCPS y)  $ \y2 ->
    runCont (addCPS x2 y2) $ k

ghci> runCont (pythagorasCPS 3 4) id
25

Cont monad

newtype Cont r a = Cont { runCont :: (a -> r) -> r }

instance Monad (Cont r) where
    return :: a -> Cont r a
    return a =
    
    (>>=) :: Cont r a -> (a -> Cont r b) -> Cont r b
    Cont arr >>= f =

instance Monad (Cont r) where
    return :: a -> Cont r a
    return a = Cont ($ a)

    (>>=) :: Cont r a -> (a -> Cont r b) -> Cont r b
    Cont arr >>= f = Cont $ \br -> arr $ \a -> runCont (f a) br

    -- arr :: (a -> r) -> r
    -- br  :: (b -> r)
    -- f   :: a -> Cont r b

Example (Cont monad)

addCPS :: Int -> Int -> Cont r Int
addCPS x y = return $ x + y

squareCPS :: Int -> Cont r Int
squareCPS = return . square

pythagorasCPS :: Int -> Int -> Cont r Int
pythagorasCPS x y = squareCPS x >>= \x2 ->
                    squareCPS y >>= \y2 ->
                    addCPS x2 y2