Dijkstra là gì? Tìm đường đi ngắn nhất Dijkstra cài đặt bằng C/C++

Trong bài viết này, chúng ta sẽ nghiên cứu Dijkstra C++ là gì, bên cạnh đó là những ví dụ về thuật toán Dijkstra và mã C++ của nó cùng với đầu ra tương ứng. Để bắt đầu tìm hiểu về những điều này trong C++ thì mới bạn đọc phần tiếp theo.

👉👉👉Follow social của Aptech:

https://aptech.fpt.edu.vn/thuat-toan-dijkstra.html

https://www.besport.com/post/41765263

https://baskadia.com/post/6qik5

Thuật toán Dijkstra C++ là gì?

Thuật toán Dijkstra C++ thường xuyên được sử dụng và nó còn mang tên gọi khác là thuật toán đường đi ngắn nhất. Dùng để tìm đường đi ngắn nhất giữa các nút của biểu đồ. Thuật toán tạo cây các đường đi ngắn nhất từ đỉnh nguồn xuất phát từ tất cả các điểm khác trong đồ thị.

Nó khác với cây bao trùm tối thiểu vì khoảng cách ngắn nhất giữa hai đỉnh có thể không được bao gồm trong tất cả các đỉnh của đồ thị. Thuật toán hoạt động bằng cách xây dựng một tập hợp các nút có khoảng cách tối thiểu từ nguồn. Ở đây, thuật toán Dijkstra sử dụng cách tiếp cận tham lam để giải quyết vấn đề và tìm ra giải pháp tốt nhất.

Khi nào thì thuật toán Dijkstra C++ hoạt động và khi nào không thành công?

Thuật toán Dijkstra C++ chỉ hoạt động với đồ thị có trọng số dương. Trong khi chạy một thuật toán, trọng số của các cạnh phải được thêm vào để tìm đường đi ngắn nhất giữa các nút. Nếu có trọng số âm trong biểu đồ, thì thuật toán sẽ không hoạt động.

Hãy nhớ rằng sau khi bạn đánh dấu nút là "đã truy cập", đường dẫn hiện tại đến nút là đường dẫn ngắn nhất để đến nút đó. Do đó, nếu bạn có trọng số âm, nó có thể thay đổi bước này nếu tổng trọng số giảm đi.

Hơn nữa, khi hiểu thuật toán Dijkstra, câu hỏi đặt ra là liệu đó là BFS hay DFS. Giữa hai cái này thường thì mức độ ưu tiên sẽ dành cho BFS nhiều hơn là DFS. Về cơ bản, bạn có thể tìm thấy một số cấu trúc thiết yếu của BFS bên trong thuật toán Dijkstra, thành thật mà nói, nó còn hơn cả thuật toán BFS.

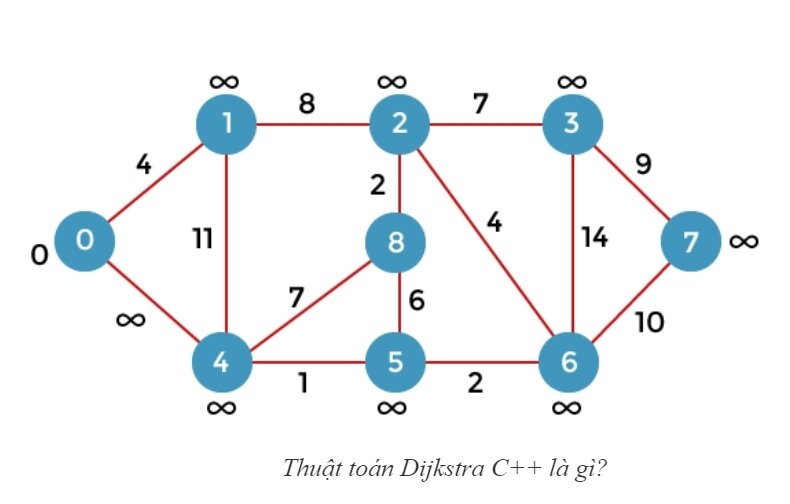
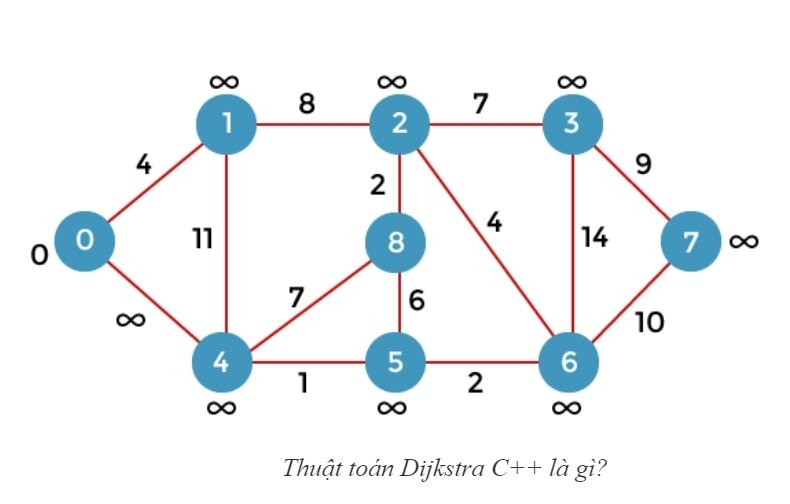
Để biết thuật toán Dijkstra hoạt động như thế nào, hãy xem các bước bên dưới để hiểu chi tiết:

Đánh dấu tất cả các đỉnh
Đánh dấu đỉnh nguồn là 0 và tất cả các đỉnh khác là vô cùng
Coi đỉnh nguồn là đỉnh hiện tại
Tính độ dài đường đi của tất cả các đỉnh lân cận từ đỉnh hiện tại bằng cách cộng trọng số của cạnh trong đỉnh hiện tại
Nếu độ dài đường dẫn mới nhỏ hơn độ dài đường dẫn trước đó thì hãy thay thế nó nếu không thì bỏ qua nó
Đánh dấu đỉnh hiện tại là đã thăm sau khi thăm đỉnh lân cận của đỉnh hiện tại
Chọn đỉnh có độ dài đường dẫn nhỏ nhất làm đỉnh hiện tại mới và quay lại bước 4.
Lặp lại quá trình này cho đến khi tất cả các đỉnh được đánh dấu là đã thăm.
Khi chúng tôi thực hiện thuật toán, chúng tôi có thể quay lại đỉnh nguồn và tìm đường đi ngắn nhất của mình.

Vậy là qua bài viết bạn đã hiểu được định nghĩa của Dijkstra C++ cũng như các điều kiện để nó hoạt động. Nếu bạn cần thêm thông tin về cách lập trình này thì hãy truy cập website của chúng tôi và đọc thêm các bài viết.