Power index-Based Ranking–Semantics

Master degree in Computer Science

Candidate
Francesco Faloci

Advisors
Stefano Bistarelli
Francesco Santini

Power index-Based Ranking–Semantics
  • Argumentation
  • Ranking Semantincs
  • Power Indexes
  • PI based Ranking-Semantics
Power index-Based Ranking–Semantics
  • Argumentation
  • Ranking Semantincs
  • Power Indexes
  • PI based Ranking-Semantics
Argumentation
Argumentation
  • Bob: «I want to go soccer»
     
  • Alice: «I want to go to the theater»
     
  • Bob: «My Ex is in the theater»
     
  • Alice: «You don't have an Ex»
Argumentation

«I want to go soccer»

«I want to go to the theater»

«My Ex is in the theater»

«You don't have an Ex»

Argumentation

Argumentation Framework

Argumentation

Abstract Argumentation Framework

  • set of abstract elements "A", called  arguments
     
  • set of binary relations "R", on the elements  of A

F = CC

Argumentation

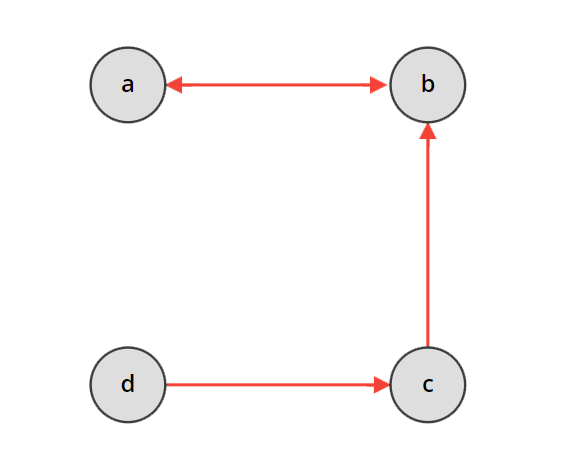
A: { a, b, c, d }

R: { (a,b), (b,a), (c,b), (d,c) }

Argumentation
  • Acceptability
    an argument a ∈ A is acceptable with respect to S ⊆ A ⇔
    S defends a: ∀ b ∈ A such that (b,a) ∈ R, ∃ c ∈ S such that (c,b) ∈ R
     
  • Conflict-free
    a set of arguments S is conflict-free if there is no attack between its arguments: ∀ a,b ∈ S, (a,b) ∉ R
     
  • Admissible
    a set of arguments S is admissible ⇔ it is conflict-free and all its arguments are acceptable with respect to S.
Argumentation: Sets
  • Conflict-free
    {} {1} {2} {3} {4} {1 3} {1 4} {2 4}
     
  • Admissible
    {} {1} {4} {1 4} {2 4}

{} {1} {2} {3} {4} {1 2} {1 3} {1 4} {2 3} {2 4} {3 4}
{1 2 3} {1 2 4}​ {1 3 4}​ {2 3 4}​ {1 2 3 4}​

Argumentation: Semantics
  • Complete
    S is a complete extension of F ⇔ it is admissible and every acceptable argument with respect to S belongs to S.
     
  • Prefered
    S is a preferred extension of F ⇔ it is a maximal element among the admissible sets with respect to F.
     
  • Stable
    S is a stable extension of F ⇔ it is a conflict-free set that attacks every argument that does not belong in S.
     
  • Ground
    S is the (unique) grounded extension of F ⇔ it is it is the smallest element among the complete extensions of F.
Argumentation: Semantics
  • Complete
    S is a complete extension of F ⇔ it is admissible and every acceptable argument with respect to S belongs to S.
  • Complete
    {4} {1 4} {2 4}
Argumentation: Semantics
  • Prefered
    S is a preferred extension of F ⇔ it is a maximal element among the admissible sets with respect to F.
  • Preferred
    {1 4} {2 4}
Argumentation: Semantics
  • Stable
    S is a stable extension of F ⇔ it is a conflict-free set that attacks every argument that does not belong in S.
  • Stable
    {1 4} {2 4} 
Argumentation: Semantics
  • Ground
    S is the (unique) grounded extension of F ⇔ it is it is the smallest element among the complete extensions of F.
  • Ground
    {4} 
Argumentation: Semantics
  • Complete
    {4} {1 4} {2 4}
     
  • Preferred
    {1 4} {2 4}
     
  • Stable
    {1 4} {2 4}
     
  • Ground
    {4}

{} {1} {2} {3} {4} {1 2} {1 3} {1 4} {2 3} {2 4} {3 4}
{1 2 3} {1 2 4}​ {1 3 4}​ {2 3 4}​ {1 2 3 4}​

Argumentation: Labelling
in(L) = \{a \in A \mid L(a) = in \}
out(L) = \{a \in A \mid L(a) = out \}
undec(L) = \{a \in A \mid L(a) = undec\}

Another Method to express acceptability of argument

  • ∀ a,b ∈ A, if A ∈ in(L) and (b,a) ∈ R, then b ∈ out(L)
     
  • ∀ a ∈ A, if a ∈ in(L), then ∃ b ∈ A such that A ∈ in(L) and (b,a) ∈ R
Power–index Based Ranking–Semantics
  • Argumentation
  • Ranking Semantincs
  • Power Indexes
  • PI based Ranking-Semantics
Ranking Semantincs
Ranking Semantincs

a ≻ d ≻ c ≻ b

Ranking Semantincs

Categorize

(..)

Ranking Semantincs

Discussion-based semantics

(..)

Burden-based semantics

(..)

Ranking Semantincs

Two-person zero-sum game semantics

(..)

Power index-Based Ranking–Semantics
  • Argumentation
  • Ranking Semantincs
  • Power Indexes
  • PI based Ranking-Semantics
Power indexes

Arancio

Bianca

Celeste

20%

40%

15%

Voting Game!

Power–indexes

Arancio

Bianca

Celeste

20%

40%

15%

60%

Power–indexes

A: 20%

B: 40%

C: 15%

Voting Game

Power-Index

Calculate the marginal contribution of each agent

Power–indexes

A: 20%

B: 40%

C: 15%

let's try the... Shapley Value ! (SV)

SV (A) = 0,5

SV (B) = 1

SV (C) = 0,5

B ≻ A ≃ C

  • if a coalition S reaches the 51% it values 1, 0 otherwise

  • we consider only minimal coalition: not the whole set

  • Only coalitions (A,B) and (B,C) are winning

Power indexes: Shapley Value

We used the characteristic function         defined on the coalition S that contains the agent i, as following:

and the Shapley Value formua for all the agents (i) as following:

\phi_i(v)= \sum_{S \subseteq N \setminus \{i\} }\frac{|S|! \; (|N| - |S| - 1)! }{|N|!} \;\; v_{S_i}
v_{S_i} = v(S \cup \{i\}) - v(S)
v_{S_i} 
Power–indexes: MORE Indexes

Banzhaf Power Index

Deegan-Pakel Index

Johnston Index

\beta_i(v) = \frac{1}{2^{|N|-1}} \sum_{S \subseteq N \setminus \{i\} } v_{S_i}
\rho_i(v) = \frac{1}{|M(v)|} \sum_{S \subseteq M_i(v) \setminus \{i\} \\ S\neq \emptyset} \frac{v_{S_i}}{|S|}
\gamma_i(v) = \sum_{S \subseteq N \setminus \{i\} \\ \varkappa(S) \geq 1} \frac{v_{S_i}}{\varkappa(S)}
Power–index Based Ranking–Semantics
  • Argumentation
  • Ranking Semantincs
  • Power Indexes
  • PI based Ranking-Semantics
PI Ranking–Semantics

AF

Voting Game

Ranking Semantincs

PI Ranking–Semantics

A: { a, b,  ... }

AF  Dung's Semantics

Coalitions :

Agents :

Characteristic function         based on Acceptability of arguments

v_{S_i} 
PI Ranking–Semantics

A ⇒ agents

  ⇒ coalitions

v_{S_i}

 {1} {2} {3} {4}

Conflict-free, Admissible, Complete,  Preferred, Stable,  Ground

\sigma
PI Ranking–Semantics

Characteristic Function(s)

v^{I}_{\sigma,F}(S) = \begin{cases} 1, & \text{if } S \in \mathit{in}(L_\sigma) \\ 0, & \text{if } otherwise \end{cases}\hspace{4em}
v^{O}_{\sigma, F}(S) = \begin{cases} 1, & \text{if } S \in \mathit{out}(L_\sigma) \\ 0, & \text{if } otherwise \end{cases}

Given      a Dung semantics and         the set of all possible labellings on F satisfying     , we define:

\sigma
L_\sigma
\sigma
PI Ranking–Semantics

Formal Definition

S. Bistarelli, F. Faloci, F. Santini, and C. Taticchi. A Tool For Ranking Arguments Through Voting-Games Power Indexes. In Proceedings 34th CILC, volume 2396 of CEUR Workshop Proceedings, pages 193–201. CEUR-WS.org, 2019.

PI Ranking–Semantics

(Esempio applicativo con SV e Banzhaf)

PI Ranking–Semantics

(4 chiacchiere su conarg)

PI Ranking–Semantics

(Elenco delle pubblicazioni fatte su sta roba)

PI Ranking–Semantics

Future

PI Ranking–Semantics

/end

Made with Slides.com