stack & queue

Stack

LIFO (last-in-first-out)

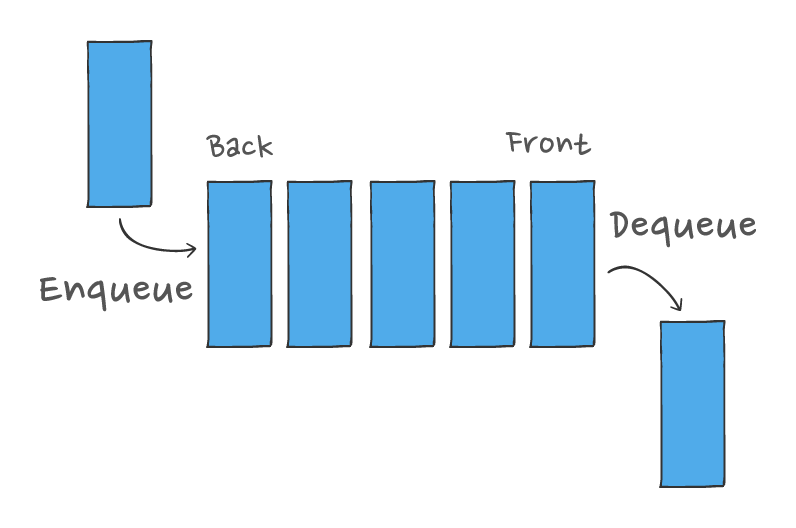
Queue

FIFO (first-in-first-out)

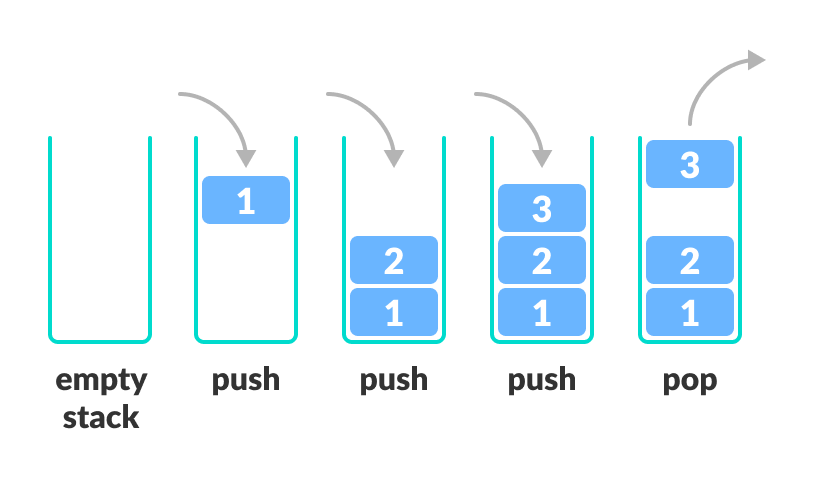
Stack

Queue

s

q

s.top()

s.push(t)

t

s.pop()

是否為空：s.empty()

q.push(t)

q.pop()

q.front()

是否為空：q.empty()

Example 1

用stack和queue輸入和輸出

#include <iostream>
#include <queue>
// #include <bits/stdc++.h>
using namespace std;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    queue<int> Q;
    int n,t;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>t;
        Q.push(t);
    }
    for(int i=0;i<n;i++){
        t=Q.front();
        cout<<t<<" ";
        Q.pop();
    }
    return 0;
}
#include <iostream>
#include <stack>
// #include <bits/stdc++.h>
using namespace std;

int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    stack<int> S;
    int n,t;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>t;
        S.push(t);
    }
    for(int i=0;i<n;i++){
        t=S.top();
        cout<<t<<" ";
        S.pop();
    }
    return 0;
}

Exercise 1

zerojudge_e447 queue練習

Exercise 1_ans

#include <bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n,t;
    queue<int> q;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>t;
        if(t==1){
            int p;
            cin>>p;
            q.push(p);
        }
        else if(t==2){
            if(!q.empty()){
                cout<<q.front()<<'\n';
            }
            else{
                cout<<-1<<'\n';
            }
        }
        else if(t==3){
            if(!q.empty()){
                q.pop();
            }
        }
    }
    return 0;
}

Checked for Balanced Brackets

括弧配對

想法：

用一個堆疊(Stack)，每次讀入字串的一個字元。

如果是左括弧，就把它push進去Stack裡面

如果是右括弧，就把它和堆疊最上面的字元配對，如果不符則error

如果最後堆疊還有剩下括弧是error

如果都沒錯，則是平衡的

())

))

(

))

(

成功配對

pop

)

沒有配對

error

Answers

#include <bits/stdc++.h>
using namespace std;
int sol(){
  stack<int> S;
  char in[210], ch[7]="([{)]}";
  while(cin>>in){
	bool error=false;
	int len=strlen(in);
	for(int i=0;i<len;i++){
		int sym=strchr(ch,in[i])-ch;
		if(sym>=6){
			return -1;
		}
		if(sym<3){
			S.push(sym);
		}
		else{
			if(S.empty()||sym!=S.top()+3){
				error=true;
				break;
			}
			S.pop();
		}
	}
	if(!S.empty())
		error=true;
	(error)?cout<<"no\n":cout<<"yes\n";
	return 0;
	}
}

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	while(sol()==0);
	return 0;
}

Question

  1. 為什麼括弧有六種卻要ch卻要宣告七格？
  2. 如果不先宣告len=strlen(in)，而在for迴圈裡面寫i<strlen(in)會有什麼缺點？
  3. 想想int sym=strchr(ch, in[i])-ch 這句中的指標怎麼轉換的？ (strchr用法) 提示：陣列的名字是一個？
  4. (error)?cout<<"no\n":cout<<"yes\n"; 是什麼意思？
  5. 為什麼要設一個布林型態的error，而不能在遇到錯誤的時候直接cout<<"no"然後break？

priority_queue

n.優先考慮的事

優先佇列

How to use priority_queue?

宣告

priority_queue<型態> 名字;

priority_queue<int> pq;

加入元素

pq.push(x);

查詢最大

pq.top()

因為priority_queue會把加入的元素由大到小排序

刪除最大

pq.pop()

是否為空

pq.empty();

P.s. 不在APCS範圍內

Example_2

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

int main(){
	ios::sync_with_stdio(0);
    	cin.tie(0);
	int n;
	cin>>n;
	priority_queue<LL> PQ;
	for(int i=0;i<n;i++){
		int m;
		cin>>m;
		PQ.push(-(LL)m);
	}
	LL cost=0;
	for(int i=0;i<n-1;i++){
		LL m=PQ.top();
		PQ.pop();
		m+=PQ.top();
		PQ.pop();
		PQ.push(m);
		cost+=m;
	}
	cout<<-PQ.top()<<'\n'<<-cost<<'\n';
	return 0;
}

Ans

Greedy Algorithm

adj. 貪婪的

貪心演算法

Greedy

如果面額改成[1,7,8,15]呢？

如果測資是14元，依照貪心演算法會是8*1+1*6，需要7枚代幣。

但這可以靠7*2，2枚代幣解決，所以貪心演算法不適用於所有情況。

Made with Slides.com