Algorithm Problem Solving

이강석(gangseok514@gmail.com)

Notice

https://www.acmicpc.net

Notice

  • 알고리즘 기초문제를 풀 수 있는 수준으로 작성되었습니다.
  • 특정 수학지식, 알고리즘을 이용한 문제풀이는 최대한 배제되어 있습니다.

Notice

  • 이 과정은 알고리즘 기초 입문자에게 흥미와 자신감을 주기위해 만들었습니다.

Notice

  • 아래 링크의 문제들을 강의자료의 연습문제로 병행하면 좋습니다.

링크

알고리즘?

알고리즘이란?

  • 알고리즘이란 어떠한 문제를 해결하기 위한 여러 동작들의 모임
  • 수학과 동일하다. 특정 알고리즘을 배우고 문제풀이에 응용할 수 있으면 된다.

알고리즘

  • 알고리즘 공부에 가장 효과적인 방법은 문제풀이!
  • 수능문제를 푸는 것이 아니기 때문에 원리에 대해 심도있게 깨우치는 것보다 가능한 많이 풀어보는 것이 중요
  • 많이 풀다보면 응용력이 생김

알고리즘 공부하면서 느낀점

  • 코딩하기 전에 생각하는 습관이 길러진다.
  • 조건을 최대한 명확히 하여 계산의 오류가 줄어든다.
  • 언어에서 제공하는 자료구조의 성능을 이해하고 적재적소에 활용할 수 있다.
  • 하지만 소프트웨어를 공부하는 하나의 과목일 뿐 소프트웨어 전문가가 되는 것은 아니다.

추천하는 책

  • 알고리즘 문제해결 전략(구종만)
  • 다양한 예제로 학습하는 데이터 구조와 알고리즘(C/Java)
  • '16.9월에 나올 최백준님의 책

알고리즘 온라인 채점 사이트

공부하는 방법

  • 포기할 줄 알아야 함
    • 2시간정도 고민해보고 안되면 풀이를 본다.
    • 1개를 3일 동안 보는 것보다 3개를 하루동안 보는 것이 낫다. 
    • 그래프를 모르는데 그래프 문제를 계속 고민해봤자 의미 없다.
  • 질문한다
    • 풀이를 봐도 이해가 안되면 질문한다.
  • 유사 문제를 많이 풀어본다.
  • 그래도 이해가 안되면 다른 문제를 푼다.
    • Keep 해놓고 나~중에 본다.
  • 이해가 되면 오답노트를 꼭 만들자

공부하는 방법

  • 다른 사람이 푼 풀이도 본다.
    • 내가 푼 것보다 더 세련된 코드를 보고 배우자
  • 동기부여가 되는 방법을 찾아본다.
    • 스터디그룹
      • 시간이 없어 못푼다면 모였을때 다 같이 풀어본다.
      • 모일시간도 없다면 메일이라도 주고받자.
    • 알거라고 생각하는 쉬는 문제부터 풀어본다.
      • 좌절감이 줄어든다

문제풀이 기초전략

Step1. 문제를 적는다.

  • 문제를 정확히 이해하는 것이 중요
  • 문제를 이해했으면 자신의 표현으로 다시 정리한다
  • 문제의 입력크기의 상한에 유의

Step2. 연필과 종이로 풀기

  • 연필과 종이를 이용하여 문제를 풀어본다
    • 일반적인 케이스에 대해 적용 가능한 풀이법 
    • 풀이 과정을 절차적 단계로 분해 가능
      • 머릿속의 복잡한 과정을 풀어내는 훈련

Step2. 연필과 종이로 풀기

  • 예) 16 과 24의 최대공약수를 구하라!
    • 음........ 8이군!!!!!

Step2. 연필과 종이로 풀기

  • 예) 16 과 24의 최대공약수를 구하라!
    • 음........ 8이군!!!!!
      • 여기서 그치면 알고리즘이 아님
      • 모든 계산 단계에서
        • 직관적 요소를 배제
        • 기계적 계산요소로만 구성해야 함

Step2. 연필과 종이로 풀기

  • 예) 16 과 24의 최대공약수를 구하라!
    • 공약수는 두 수를 모두 나누는 자연수
    • 1보다는 같거나 크고 두 수보다는 같거나 작은 수
    • 그럼 1부터 16까지 차근차근 다 나눠보자

Step2. 연필과 종이로 풀기

  • 예) 16 과 24의 최대공약수를 구하라!
    • 그럼 1부터 16까지 차근차근 다 나눠보자
      • 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
      • ​​8이 정답이구나!!

Step3. 알고리즘 구성하기

  • 연필과 종이로 문제를 해결한 과정을 알고리즘으로 구성
  • 예) 두 수 a와 b의 최대공약수를 구하라!
    1. c = min(a, b)​
    2. i for 1 to c
      • find maximum i that divides both a and b

Step4. 시간복잡도 계산하기

  • 앞 단계에서 구성한 알고리즘의 시간 복잡도를 분석
  • 최대 입력 사이즈를 대입하여 예상 수행 시간을 가늠
    • 만약 a, b의 상한이 10억이라면?
    • 비효율적이면 더 효율적인 방법을 생각

Step5. 구현하기

  • 알고리즘을 프로그래밍 언어로 옮겨 적기
int gcd(int a, int b) {
    int great_common_divisor = 1;
    for (int k = 1; k <= a && k <= b; ++k) {
        if (a % k == 0 && b % k == 0) {
            great_common_divisor = k;
        }
    }
    return great_common_divisor;
}

Step6. 테스트

  • 구현한 코드를 테스트
  • 테스트 결과에 따라 다른 전략
    • 테스트 가이드 참고

Product 를 만드는 것이 아님

  • 알고리즘 문제풀이 역량은 소프트웨어 역량중에 한가지 일뿐
  • 문제를 풀기위해 최소한으로 코드를 작성해야 한다.
  • 길어야 200줄!

시간/공간 복잡도

시간복잡도

  • 시간 복잡도를 이용하면 작성한 코드가 시간이 얼마나 걸릴지 예상할 수 있다.
  • 표기법으로 대문자 O를 사용한다.
  • 영어로는 Big O Notation
  • 입력의 크기에 대해서 시간의 상한을 나타내는 방법
    즉, 최악의 케이스에 걸리는 시간을 나타낸다.

시간복잡도

  • 아래 소스는 1부터 N까지 합을 계산하는 소스이다.

 

 

 

 

 

 

  • 시간복잡도 : O(N)
int sum = 0;
for (int i=1; i<=N; i++) {
    sum += i;
}

시간복잡도

  • 대표적인 시간 복잡도는 아래와 같다.
    • O(1)
    • O(lgN)
    • O(N)
    • O(NlgN)
    • O(N^2)
    • O(N^3)
    • O(2^N)
    • O(N!)

시간복잡도

  • 대표적인 시간 복잡도는 아래와 같다.
    • O(1)
    • O(lgN)
    • O(N)
    • O(NlgN)
    • O(N^2)
    • O(N^3)
    • O(2^N)
    • O(N!)

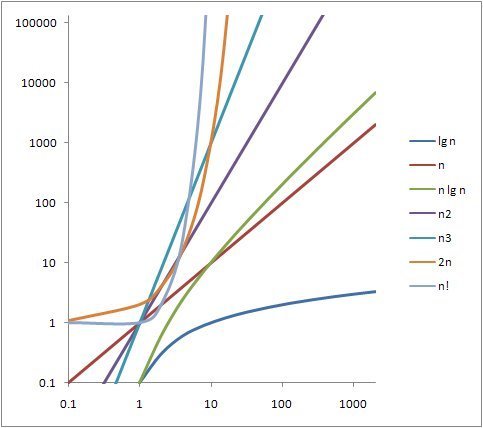
시간복잡도

  • 1억번의 연산이 걸리는 시간은 대략 1초이다.
  • 요즘은 컴퓨터 성능이 좋아져서 3억번이라고도 함

시간복잡도

  • 1초가 걸리는 입력의 크기
    • O(1)
    • O(lgN)
    • O(N) : 1억
    • O(NlgN) : 5백만
    • O(N^2) : 1만
    • O(N^3) : 500
    • O(2^N) : 20
    • O(N!) : 10

시간복잡도

  • 시간복잡도가 여러개일 경우 큰 것에 대해서만 계산한다.
    •  N^2+N : O(N^2)
    •  2^N+N^2 : O(2^N)

시간복잡도

  • 아래 소스는 1부터 N까지 합을 계산하는 소스이다.

 

 

 

 

 

 

  • 시간복잡도 : O(1)
int sum = 0;
sum = N*(N+1)/2;

시간복잡도

  • 아래 소스는 1부터 N까지 합을 계산하는 소스이다.

 

 

 

 

 

 

 

  • 시간복잡도 : O(N^2)
int sum = 0;
for (int i=1; i<=n; i++) {
    for (int j=1; j<=n; j++) {
        if (i == j) {
            sum += j;
        }
    }
}

시간복잡도

  • 재귀함수
    • 재귀함수인 경우 함수의 호출 횟수를 계산한다.
    • ​함수안에서 루프를 사용할 경우 재귀함수의 호출 횟수와 함수안 루프의 복잡도를 같이 계산해야 한다.
    • 재귀함수 호출시 입력크기의 변화에 따라 달리 계산해야 한다.
      • 선형 : f(i) -> f(i-1) + f(i-2)
      • 분할 : f(i) -> f(i/2) + f(i/2)

공간복잡도

  • 재귀에 따른 스택크기는 계산하기 어려우므로 재귀함수는 1만번 이상 호출하지 않도록 한다.
    • 채점 시스템 OS/사양에 따라 더 적게 혹은 더 많이 가능
  • 1차원 배열의 크기계산에는 실수가 별로 없으나 2차원일때는 조심해야한다.
    • int 형 [10000][10000] 은 무려 400mb 크기이다.
    • 함수안에서는 배열할당을 하지 말것
      • 스택 공간을 차지한다.

코딩가이드

입력

  • Scanf 사용하기
int n;
char a;
char s[100];

scanf("%d", &n); // 숫자 입력 받기
scanf("%c", &a); // 문자 입력 받기
scanf("%s", s); // 문자열 입력 받기

int x, y;
scanf("%d%d", &x, &y); // 숫자 2개 입력 받기

int age;
char name[100];

// 나이(숫자)와 이름(문자열) 입력 받기
scanf("%d%s", &age, name);

입력

  • Scanf 사용하기2
int n;
char a;
char s[100];

for(int i = 0; i < N; i++) {
    scanf("%1d", &n); // 1자리씩 입력받기
    scanf("%10s", s); // 10개 문자단위씩 입력받기
}

if(scanf("%d", &n) > 0) { // 입력이 들어왔을때
  printf("Hello");
}

/*
a
b
처럼 들어왔을때 ab 를 각각 받아야 한다면
*/

for(int i = 0; i < N; i++) {
    // %c 앞에 공백을 넣는다(n을 무시하기 위함, 하지만 컴파일 환경이 윈도우라면?)
    scanf(" %c", &a); 
}

입력

  • Scanf 사용하기3
    •  char 입력 받을 시의 유의점
      • 컴파일 환경이 윈도우라면 엔터는 '\r\n' 이다.
      • 이럴 때 엔터를 무시하려면
        scanf("%c%c", &c, &c) 로 처리해 주어야 한다.
      • scanf(" %c", &c) 로 하게 되면 문자 3개를 처리한다. 
        • 공백이 \r\n을 한꺼번에 처리함
        • 엔터를 무시하면서 입력을 받고 싶을때는 사용가능

입력

  • cin
    •  cin 은 엔터 혹은 공백을 무시한다.
    • \r\n 등은 신경쓰지 않아도 된다.
    • 다만 scanf 보다 약 2~3배 정도 느리다.
  • std::ios::sync_with_stdio(false)
    • cin 사용전에 명시하면 scanf 동등 성능이 나온다.
    • 다만, 런타임 에러가 날 가능성도 존재함

출력

  • printf 사용하기
printf("Hello world!\n"); // 개행문자는 '\n'

printf("%d + %d = %d\n", 1, 2, 1 + 2); // 1 + 2 = 3

printf("%d", x); // int 변수값 출력하기

printf("%s", s); // 문자열 변수값 출력하기

for (int tc = 1; tc <= TC; ++tc) {
    printf("Case #%d: %d\n", solve());
}

cstdio ? iostream?

  • 앞서 말했듯이 cin 은 scanf 보다 2~3배 느리다.
  • cout 의 경우도 endl을 붙일 경우 버퍼를 flush 하기 때문에 printf 보다 느릴 수 있다.
  • 결론 : scanf, printf 를 쓰자 

입출력

  • 입출력은 번갈아해도 상관없음
int main() {
    int TC;
    scanf("%d", &TC);
    for (int tc = 1; tc <= TC; ++tc) {
        int x;
        scanf("%d", &x);
        printf("Case #%d: %d\n", tc, x * x);
    }
    return 0;
}

Swap

  • Swap 함수의 구현
// 템플릿을 사용하여 범용성 있게
template<typename T>    
// 레퍼런스를 사용하여 빠르게
void swap(T& a, T& b) {    
    T t = a;
    a = b;
    b = t;
}

데이터 표현 및 범위

  • 정수형
  • 실수형
  • 문자
  • 참/거짓

정수타입

  • int
    • 4바이트
    • -20억 ~ 20억(10^9)
    • %d
  • unsigned int
    • 4바이트
    • 0~40억
    • %u
  • long long
    • 8바이트
    • -9*10^18~9*10^18
    • %lld

실수타입

  • double
    • 8바이트
    • %lf

문자타입

  • char
    • 1바이트
    • ASCII
      • '0'(숫자 영) = 48
      • 'A' = 65
      • 'a' = 97
    • 숫자와 대소문자 사이에는 특수기호들이 있으니 특수기호도 입력으로 들어올 경우에는 범위체크를 합쳐서 하지 말것
      • ex) if(c >= '0' && c <= 'z')

문자타입2

  • char
    • 1바이트 정수형으로 쓰인다
    • 즉, 정수연산을 할 수 있다.
      • '1' - '0' = 1
      • 'A' + 3 = 'D'
      • 'G' + 32 = 'g'

참/거짓타입

  • bool
    • 1바이트
      • int 에 0/1로 담지 말고 bool 타입을 쓰자
    • true or false

타입선택의 중요성

  • 최소/최대 혹은 합을 구할 시 int 값 이상이라면 long long 을 써야 한다.
  • 너무 큰 경우에는 특정 값으로 나누어서 나타내라는 조건이 문제에서 언급된다.(1,000,000,007 = 소수)

형변환시 유의점

float f = 278.90f;
int i = f*100;

printf("%d", i);
  • 27890 이 예상되지만 27889가 나올 수도 있다.
    이것은 float형의 오차로 인해 발생하는 문제로 이를 해결하기 위해서는 보통 다음과 같이 처리한다.
float f = 278.90f;
int i = (f*100 + 0.5);

printf("%d", i);

배열 선언

  • 큰 배열은 전역에서 선언
    • 동적할당 X
    • 인풋 상한으로 할당한다.
  • 배열 크기에 여유를 주기
    • 풀이 전략에 따라 1부터 시작하는게 편할 수도 있다
       
const int MAX_N = 1000;

int N;
int A[MAX_N + 1][MAX_N + 1];

int main() {
    ...
    return 0;
}

변수 선언

  • 한 변수는 한 가지 용도로만 사용하기
    • 한 변수를 두 가지 이상 용도로 재사용 하지 말자
  • 변수 이름을 의미 있는 것으로
    • a, b, c, d, ... 이런식으로 이름 지으면 나중에 헷갈림

초기화

  • 변수 초기화
    • 특히 전역 변수
    • 일반 알고리즘 채점 사이트에서는 주로 케이스별로 매번 실행하기 때문에 초기화가 거의 필요없지만, TC를 한꺼번에 실행하는 경우에는 특히 주의해야한다.
    • init() 함수를 만들어 놓고 항상 초기화하는 습관을 가진다.
      • 입력의 크기 만큼만 하도록 한다. 예를 들어 범위로 쓸 N의 최대가 10만이지만 하나의 케이스 크기가 100으로 들어왔다면 100만큼만 초기화하자.

초기화

  • 동적할당한 메모리 해제(애초부터 사용하지 말자)

테스트가이드

테스트에 임하는 자세

  • 주어진 샘플 테스트가 맞았다고 방심하지 말자!
    • 실제 환경에서는 훨씬 다양한 케이스가 있다. 
  • 스스로 테스트 케이스를 작성
  • 디버그는 눈으로 하는 습관을 기르자

테스트 케이스 만들기1

  • 손과 종이로 풀 수 있는 최대한 크고 복잡한 케이스
    • 크게, 복잡하게, 여러개 만들기
    • 다양한 인풋에 대해 올바르게 동작하는지 확인

테스트 케이스 만들기2

  • 최대 사이즈 케이스
    • 최대 입력 사이즈에 해당하는 케이스 작성
      • 랜덤 함수(잘 사용하지 않는다)
      • 모두 같은 값
      • 1,2,3,4, ...
    • 최대 사이즈에서 시간초과, 메모리 초과 확인용

테스트 케이스 만들기3

  • 최소 사이즈 케이스
    • 최소 입력 사이즈에 해당하는 케이스 작성
    • 최소 입력에서 코너 발생 가능성
      • 구간합의 인풋이 1~1 이라면?
      • 이동거리 계산시 아예 이동이 필요없는 경우는?

오답에 대처하는 자세1

  • 오답(WA, Wrong Answer)
    • 알고리즘 검증
      • 단위 검증
    • 변수 범위 초과(음수)
    • 버퍼 오버플로우 확인
    • ​테스트 케이스 작성하여 추가 테스트
    • 코너 케이스 검증

오답에 대처하는 자세2

  • 시간 초과(TLE, Time Limit Exceeded)
    • 무한루프 가능성 검사
      • while 문을 쓸 경우 갱신이 안되는 케이스 존재
        • if else, continue 등
    • 입력 덜 받았는지 검사
      • scanf 로 무한 대기
    • ​알고리즘 개선
      • ​Big-O 단위 더 좋은 알고리즘으로 갈 것!!
      • 코드 최적화는 도움 안 됨

오답에 대처하는 자세3

  • 런타임 오류(Runtime Error)
    • 세그멘테이션 폴트 확인
      • 버퍼 오버플로우
        • 배열크기를 작게 잡음
        • 주어진 인풋과 배열크기가 일치하지 않음
      • 스택 오버플로우
        • 재귀함수를 많이 호출
        • 함수안에 큰 변수를 선언함

오답에 대처하는 자세4

  • 일부 케이스만 정답
    • 반절 정도만 맞음 : 변수 범위가 잘못된 가능성 높음
      • int -> long long,  배열 범위 초과
    • 90% 이상 맞음 : 최적화가 덜 됨
    • 딱 몇개만 틀림 : 예외 케이스 고려 안함
  • 채점 시스템에 따라 달라지지만, 총 100개 중에 50개 맞았다는
    의미는 1~50번 TC 까지 맞았다는 얘기가 아님
    • 100개 중에 순서없이 맞은게 50개라는 의미
  • 채점 시스템에 따라 컴파일시 -O2 옵션을 안줄 수도 있음
    • 수행시간 단축이 목표라면 세밀한 최적화가 필요

디버깅

  • 눈으로 디버깅하기
  • 로그 출력

 

 

 

 

 

 

 

  • 디버거 사용 - 최후의 상황에만 사용하자
#if 1
#define PA(X, ...) printf(X, __VA_ARGS__)
#define P(X) printf(X)
#else
#define PA(X, ...)
#define P(X)
#endif

int main() {
    P("Hello!");
    PA(" %s", "world");
}

디버깅

  • 수행시간 측정 방법

 

 

 

 

 

 

 

 

#include <ctime> or <time.h>


clock_t t1, t2;
t1 = clock();
{
    Code
}
t2 = clock();
printf("time: %lf\n", (double)(t2-t1)/CLOCKS_PER_SEC);

수학 기초

나머지 연산

  • (a + b) % m = ( a % m + b % m) % m
  • (a * b) % m = ( a % m * b % m) % m
  • '특정 수로 나눈 나머지를 구하라' 는 문제는
    • 결과값이 변수크기를 초과하기 때문
    • 당연히 다 합쳐서 구하면 안된다.
    • 부분값이 구해질 때마다 나머지를 구할 것

최대공약수(GCD)

  • 유클리드 호제법
    • a를 b로 나눈 나머지를 r 이라 할때
    • GCD(a, b) = GCD(b, r) 과 같다.
    • r 이 0이면 b 가 최대공약수
    • GCD(24, 16) = GCD(16, 8) = GCD(8, 0) = 8

최대공약수(GCD)

  • 유클리드 호제법
    • 루프를 사용한 구현
int GCD(int a, int b) {
    while(b != 0) {
        int r = a % b;
        a = b;
        b = r;
    }
    return a;
}

※ 두 수의 크기 순서는 고려하지 않아도 된다.

최대공약수(GCD)

  • 유클리드 호제법
    • 재귀 함수를 사용한 구현
int GCD(int a, int b) {
    return b == 0 ? a : GCD(b, a % b);
}

※ 호출 횟수는 숫자가 커져도 많지 않으므로 고려하지 않아도 된다

최대공약수(GCD)

  • 3개 이상
    • GCD(a, b, c) = GCD(GCD(a,b), c)

최소공배수(LCM)

  • L = G * (A/G) * (B/G) = A * B / G

소수

  • 약수가 1과 자신 밖에 없는 수
    • 2보다 크거나 같음
    • N-1보다 작거나 같은 자연수로 나누어 떨어지면 안됨
  • 2, 3, 5, 7, 11, 13, 17, 19, 23....
  • N이 소수인지 확인하는데 필요한 시간복잡도 : O(루트N)
    • N이 소수가 아니라면 N = a * b로 나타낼수 있고
      a 와 b 의 차이가 가장 작은 경우는 루트 N이다.
      따라서 루트N까지만 검사해보면 된다.

소수

Text

bool prime(int n) {
    if (n < 2) return false;
    for (int i = 2; i*i <= n; i++) {
        if (n % i == 0) return false;
    }
    return true;
}

소수

  • 1~N 까지 모든 소수를 구하는 방법
    • 에라토스테네스의 체

팩토리얼

  • N! = 1 * 2 * 3 * ... * N
  • 시간복잡도에서 가장 큰 값
  • 10! = 3628800

조합(이항계수)

  • n 개 중에서 k 개를 순서없이 고르는 방법 : nCk
  • n! / (k!*n-k)! = (n * n-1 * ... * n-k+1) / k!

조합(이항계수)

  • 파스칼의 삼각형
    • 이항 계수를 삼각형 모양으로 배열
    • 첫줄과 마지막줄은 1이다.
    • 나머지수는 윗줄의 왼쪽과 오른쪽 수를 더해서 구함

조합(이항계수)

  • 파스칼의 삼각형
    • C[n][0] = 1, C[n][n] = 1
    • C[n][k] = C[n-1][k-1] + C[n-1][k] (1 < k < n)

선형 자료구조

Linear DataStructure

선형 자료구조

  • 자료를 일렬로 저장하는 자료구조
    • 배열
    • 리스트
    • 스택
    • 큐

배열

  • 연속된 공간에 자료를 저장
    • O(1) : 인덱스를 이용하여 임의요소에 바로 접근
      • 특정위치의 값을 읽기
      • 특정위치에 값을 넣기(바꾸기)
    • O(N)
      • 특정값을 찾기
      • 변형을 통해 복잡도를 줄일 수 있음

배열 활용

  • 데이터 저장
  • 카운팅
  • 누적합
  • 스택, 큐, 힙(우선순위큐)을 모두 배열로 구현가능
  • 문제풀이에서 무조건 사용해야할 자료구조

배열 활용

  • 카운팅
    • 주어진 숫자들의 입력갯수를 출력하시오

int N;
int a[1000], n;

for(int i = 0; i < N; i++) {
    scanf("%d", &n);
    a[n]++;
}

for(int i = 0; i < 1000; i++) {
    printf("%d ", a[i]);
}

배열 활용

  • 구간합
    • 수열 A[0], A[1], A[2], ... , A[N] 에 대하여
      A[i], ... , A[j] 까지 합을 구하라

int sum(int i, int j) {
    int res = 0;
    for (int n = i; n <= j; n++) {
        res += A[i];
    }
    return res;
}

배열 활용

  • 구간합
    • i, j 입력이 여러번(M) 주어진다면 O(NM)

배열 활용

  • Prefix Sum
    • 미리 계산해놓고, 주어진 구간을 O(1) 에 구함
      • 계산하는데 O(N)
    • S[i] = A[1] ... A[i] 까지 합
      • S[0] = 0
      • S[k] = S[k-1] + A[k] : A[k] 까지 포함한 값
    • i ~ j 구간합은(i < j)
      • sum = S[j] - S[i-1]

배열 활용

  • 구간합
const int MAX_N = 10000;
int S[MAX_N + 1];

// O(n)
int prefixSum(int n) {
    for (int i = 1; i <= n; ++i) {
        S[i] += S[i - 1];
    }
}

// O(1)
int sum(int i, int j) {
    return S[j] - S[i - 1];
}

배열 활용

  • 구간합
    • 만약 구간값이 변경되어 업데이트 해야한다면?
      • 위 코드로는 업데이트하는 i 부터 N까지 다시 더해야 하므로 O(N) 이 걸림
    • 펜윅트리(Binary Indexed Tree)
      • 숫자 1개 업데이트 : O(lgN) - PrefixSum보다 빠름
      • i ~ j 구간합 구하기 : O(lgN) - PrefixSum보다 느림
    • 용도에 따라 선택하여 사용하여야 한다.

배열 활용

  • dx, dy
    • x,y 좌표계 등을 표시하기 위해 2차원 배열을 사용할 때
      매 Step 마다 이동해야 할 갯수가 여러개라면
      이동할 상대좌표 값을 배열로 저장하여 처리
// 북 > 동 > 남 > 서 순으로 기입
int dx[] = { 0, 1, 0, -1 };
int dy[] = { -1, 0, 1, 0 };

int f(int x, int y) {
    for(int i = 0; i < 4; i++) {
        f(x + dx[i], y + dy[i]);
    }
}

배열 활용

  • 시작은 0 부터? 아님 1부터?
    • 헷갈리지 않으려면 입력값의 범위대로 넣는 것이 기본
    • 보통 1부터 한다.
      • prefix sum 의 경우도 1부터 시작
    • 인덱스 그룹이 적용되는 경우 0부터 한다.
      • 0~99 / 100 = 0, 100~199 / 100 = 1
  • 배열의 크기에는 여유를 둔다.
    • 보통 범위에서 +1을 한다.
      • 1~N 맞춰서 입력받으려면 A[N] 이 존재해야함

스택

  • 한쪽 방향에서만 자료가 들어가고 나오는 구조
  • 연산 : push, pop, empty, size, top

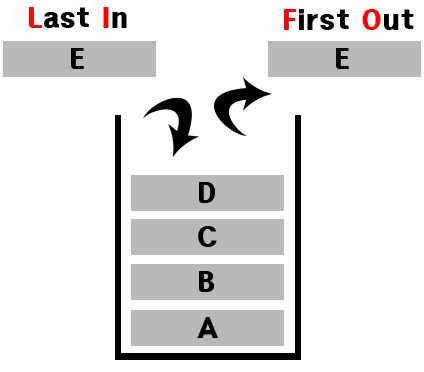
스택

  • 배열을 이용하여 스택 구현하기
const int MAX = 1000;
int stack[MAX + 1];
int stack_top;

void stack_init() {
    // 스택이 비어있는 상황이니 0으로 초기화
    stack_top = 0; 
}
int size() {
    // top값 자체가 사이즈를 의미한다. top 인덱스에는 항상 값이 비어있다.
    return stack_top; 
}
bool empty() {
    // 0이면 스택은 비어있다.
    return stack_top == 0; 
}
void push(int x) {
    // 현재 인덱스 기준으로 스택에 값을 넣은 다음 stack_top값을 증가시킨다. 
    // 즉, 현재 가리키고 있는 인덱스는 비어있다.
    stack[stack_top++] = x; 
}
int pop() {
    // 마지막에 넣은 값은 stack_top보다 1작은 인덱스에 저장되어 있다. 
    // 그러므로 감소시킨 인덱스의 값을 리턴해야한다.
    return stack[--stack_top]; 
}

큐

  • 한 쪽에서 들어가고 반대쪽에서 나오는 구조
  • 연산 : push, pop, empty, front, back, size

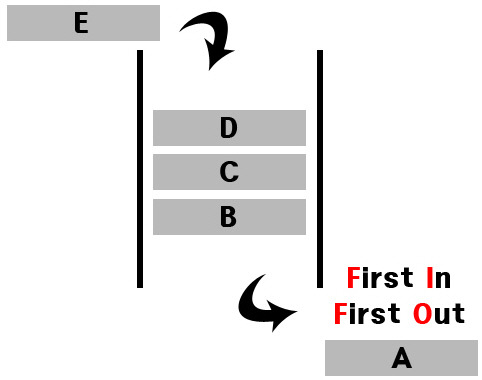
큐

  • 배열을 이용한 큐 구현
const int MAX = 10000;

int queue[MAX + 1];
int head; // head는 큐의 맨 앞의 값을 가진 인덱스이다.
int tail; // tail은 큐의 마지막 값의 다음 인덱스를 말한다.

int size() {
    return tail - head;
}

bool empty() {
    return head == tail;
}

void push(int x) {
    // tail은 비어있으니 넣고나서 증가시킨다.
    queue[tail++] = x;
}

void pop() {
    // head는 맨 앞 값이니 리턴하고 증가시킨다.
    return queue[head++];
}

정렬

  • 데이터를 어떤 순서대로 재배치 하는 것

정렬 방법과 시간복잡도

  • 비교정렬
    • 두 요소의 대소를 비교해 자리를 바꾸는 방법
    • 시간복잡도에 따른 종류 구분
      • O(N^2) : 구현이 쉬우나 느리다.
        • 버블, 삽입, 선택 정렬 등
      • O(NlgN) : 구현이 어려우나 빠르다.
        • 병합(머지), 퀵 정렬 등

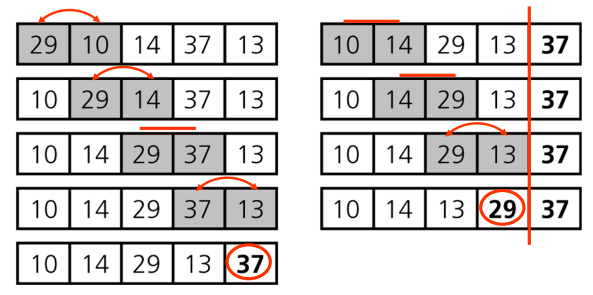
O(N^2) 정렬

  • 버블정렬
void bubbleSort(int A[], int len) {
    for (int i = 0; i < len; ++i)
        for (int j = 1; j < len; ++j)
            if (A[j - 1] > A[j])
                swap(A[j - 1], A[j]);
}

O(N^2) 정렬

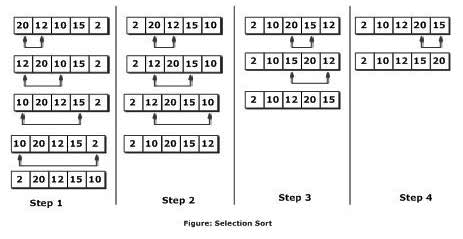
  • 선택정렬
void selectionSort(int A[], int len) {
    int min = 0;
    for (int i = 0; i < len-1; ++i) {
        min = i;
        for (int j = i + 1; j < len; ++j) {
            if (A[min] > A[j]) {
                min = j;
            }
        }
        if(min != i) swap(A[i], A[min]);
    }
}

O(NlgN) 정렬

  • 병합(머지), 퀵 정렬 등이 있다.
  • 문제풀이에 사용하기 쉬운 알고리즘은 병합정렬이다.
  • 분할정복(Divide & Conquer)의 대표적인 예

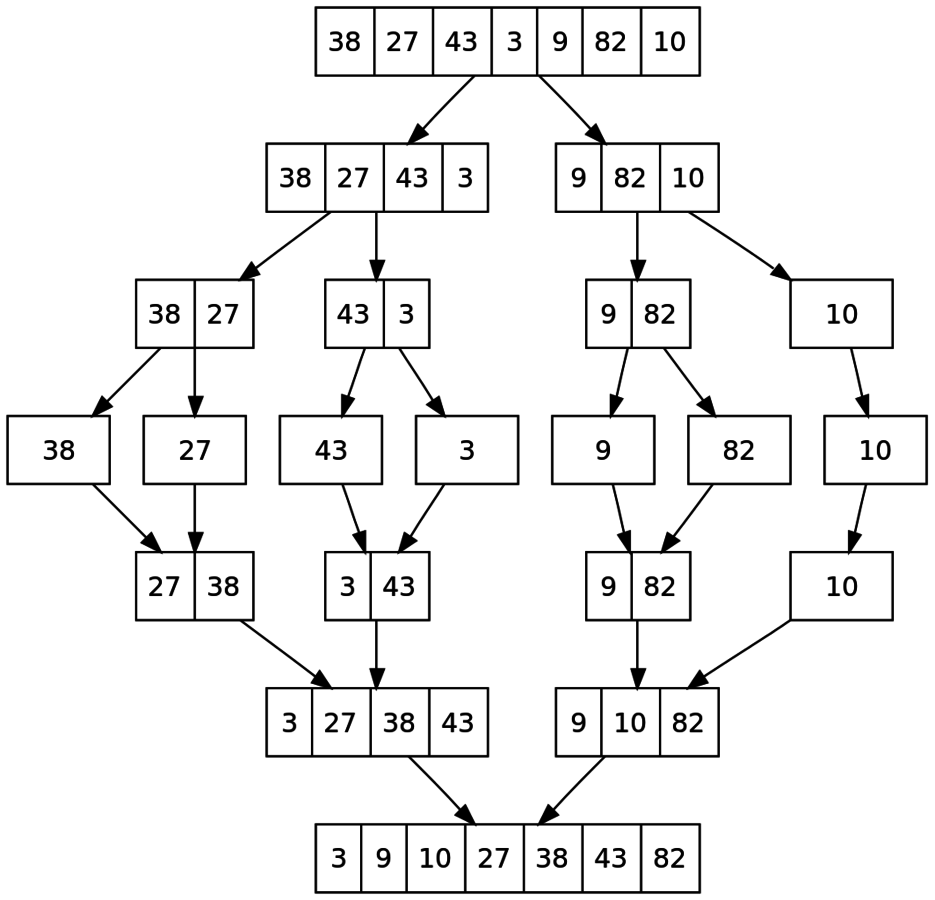
O(NlgN) 정렬

  • 보통 알고리즘 대회에서는  STL sort 를 사용하면 되므로
    구현내용까지 알 필요는 없다. 하지만 STL 같은 라이브러리
    사용이 제한된 대회라면 직접 구현해야 한다.

구간최대최소값

  • A[i], ..., A[j] 중에서 최소/최대값을 찾아 출력한다.
  • 이러한 연산이 총 M개 주어진다.
k 0 1 2 3 4 5
값 3 6 2 5 1 8

구간최대최소값

  • 방법1 : 다 해보기

 

 

 

 

  • 시간복잡도 : O(MN)
int m = a[i];
for(int k = i; k <= j; k++) {
    if(m > a[k]) {
        m = a[k];
    }
}

구간최대최소값

  • 방법2 : 미리 저장해두고 사용하기
    • D[i][j] = A[i]~A[j] 중 최소값을 저장한다.(i <= j)
      • D[i][j] = min(D[i][j-1], A[j])
    • D[i][i] = A[i]
  • 시간복잡도
    • 저장 : O(N^2)
    • 구하기 : O(1)
i\j 0 1 2 3 4 5
0 3 3 2 2 1 1
1 6 2 2 1 1
2 2 2 1 1
3 5 1 1
4 1 1
5 8
k 0 1 2 3 4 5
값 3 6 2 5 1 8

구간최대최소값

  • 미리 저장해두고 사용하기 - 구현
int d[N][N];
int a[N];
int n;

for (int i = 0; i < n; i++) {
    d[i][i] = a[i];
    for(int j = i + 1; j < n; j++) {
        d[i][j] = min(d[i][j - 1], a[j]);
    }
}

구간최대최소값

  • 방법3 : 루트 N으로 구간 나누기(Sqrt Decomposition)
    • R=루트N 이라 했을때
    • 배열을 R개의 그룹으로 나눈 다음에 G[i]에 i 번그룹의 최소/최대값을 저장하는 방식
0 1 2 3 4 5 6 7 8 9
3 6 2 5 3 1 8 9 7 3
G[0] = 2 G[1] = 1 G[2] = 7 3

구간최대최소값

  • 루트 N으로 구간 나누기
    • R=루트N 이라 했을때
    • 배열을 R크기단위로 쪼갠 최대 갯수크기로 G배열을 추가로 생성하고, G[i]에 i 번 그룹의 최소/최대값을 저장하는 방식
    • 저장하기 시간복잡도 : O(N)
for (int i = 0; i < n; i++) {
    if (i % r == 0) {
        g[i / r] = a[i];
    } else {
        g[i / r] = min(g[i / r], a[i]);
    }
}

구간최대최소값

  • 루트 N으로 구간 나누기
    • i~j 중 최소값을 구하는 방법에는 2가지 고려사항이 있음
      1. i와 j가 같은 그룹인 경우
      2. i와 j가 다른 그룹인 경우
        1. i가 속한 그룹
        2. j가 속한 그룹
        3. i와 j 사이에 있는 그룹들

구간최대최소값

  • 루트 N으로 구간 나누기
    • A[1] ~ A[9]의 최소값을 구하는 경우
0 1 2 3 4 5 6 7 8 9
3 6 2 5 3 1 8 9 7 3
G[0] = 2 G[1] = 1 G[2] = 7 3

구간최대최소값

  • 루트 N으로 구간 나누기
    • A[1] ~ A[9]의 최소값을 구하는 경우

 

 

 

  • A[1], A[2], A[9], G[1], G[2] 중에 최소값을 고르면 된다.
0 1 2 3 4 5 6 7 8 9
3 6 2 5 3 1 8 9 7 3
G[0] = 2 G[1] = 1 G[2] = 7 3

구간최대최소값

  • 루트 N으로 구간 나누기
    • A[1] ~ A[9]의 최소값을 구하는 경우

 

 

 

// A[1] 부터 A[2] 까지만
while (true) {
    if(start % r == 0) break;
    ans = min(ans, a[start]);
    start += 1;
}

// A[9] 만(반대로 체크)
while (true) {
    if(end % r == r - 1) break;
    ans = min(ans, a[end]);
    end += 1;
}

// G 체크
for (int i = start / r; i <= end / r; i++) {
    ans = min(ans, group[i]);
}

구간최대최소값

  • 루트 N으로 구간 나누기
    • 시간복잡도 : O(3루트N)

구간최대최소값

  • DP(다이나믹 프로그래밍)
    • 선처리 : O(NlgN)
    • 쿼리 : O(1)
  • 세그먼트 트리
    • 선처리 : O(NlgN)
    • 변경, 쿼리 : O(lgN)

완전탐색

Exhaustive search

완전탐색(exhaustive search)

  • 완전탐색은 모든 케이스에 대해서 일일히 다 해봐서 답을 구하는 방법을 말한다. 
  • Brute-force search 라고도 한다.
  • 루프, 재귀로 구현하여 답이 나올때까지 계산한다.
  • 대표적인 예
    • 미로탐색 : 목적지가 나올 때까지 계속 확인한다.

완전탐색(exhaustive search)

  • 해결 전략에 따른 구현법
    • 백트래킹
      • 재귀(DFS)
      • 큐(BFS)
    • 분할정복, 이진탐색
      • 루프
      • 재귀

완전탐색(exhaustive search)

  • 문제는 완전탐색으로 제한시간내에 풀 수 있는가 이다.
  • 시간 계산은 둘째 치더라도 구현하는 것도 벅찰 수 있다.
  • 하지만 순서는 반드시
    1. 입력값의 범위로 가능 시간복잡도 계산
    2. 생각한 완전탐색이 시간복잡도 내에 끝이 나는지 계산

백트래킹(Backtracking)

  • 주어진 답이 나올 때까지 검색하다가 중간에 확실히
    이 방향이 아니면 다시 이전 상태로 돌아가서 다른 경로를
    찾아보는 방법
  • 검색에 제한을 걸 수 있는 조건이 문제에 주어져야 함
  • 가지치기(Pruning) 이라는 방법으로 경우의 수를 줄인다
    • 리턴하는 조건을 많이 추가할 수록 성능이 좋아진다
  • DFS, BFS로 문제를 해결시 백트래킹 기법을 어떻게 구현하느냐에 따라 주어진  문제를 시간내에 해결할 수 있다.

재귀호출

Recursion

재귀호출(Recursion)

  • 자기자신을 호출
  • 부분이 전체와 닮아 있다.
    • 동일 작업을 반복 수행

재귀호출(Recursion)

  • 수학적 귀납법으로 정의되는 것은 재귀적 성질을 갖는다
    • 자연수
    • 피보나치 수열
    • 각종 점화식

귀납적 정의

  • 자연수
    • base case : 기저값
      • A[1] = 1
    • others
      • A[k] = A[k-1] + 1

귀납적 정의

  • 피보나치 수
    • base case : 기저값
      • f(0) = 0, f(1) = 1
    • others
      • f(k) = f(k-1) + f(k-2)

귀납적 정의

  • 피보나치 수
    • 구현해보기
int fib(int k) {
    // base cases
    if (k == 0) return 0;
    if (k == 1) return 1;
    
    // others
    return fib(k - 1) + fib(k - 2);
}

재귀적으로 풀기

  • 기저값을 제일 먼저 고려하기 > 종료조건
  • 공통된 작업을 수행

재귀호출

  • 예) 하노이 탑
    • 한 기둥에 있는 원판들을 다른 기둥으로 옮기는 게임
    • 시작 기둥, 목표 기둥, 중간에 거쳐갈 기둥. 총 3개
      • 한 번에 하나의 원판만 옮길 수 있다.
      • 큰 원이 작은 원판 위에 있을 수 없다.

재귀호출

  • 예) 하노이 탑
    • k층 탑을 A 기둥에서 B 기둥으로 옮기기
      • k 가 1인 경우
        • 그냥 옮긴다
      • k가 1보다 큰 경우
        • k-1층 탑을 A에서 C로 옮긴다.
        • k번째 원판을 A에서 B로 옮긴다.
        • k-1층 탑을 C에서 B로 옮긴다.

재귀호출

  • 예) 하노이 탑

k

k-1

A

C

B

재귀호출

  • 예) 하노이 탑

k

k-1

A

C

B

재귀호출

  • 예) 하노이 탑

k

k-1

A

C

B

재귀호출

  • 예) 하노이 탑

k

k-1

A

C

B

재귀호출

  • 예) 하노이 탑
// k 개의 원반을 from에서 to로 옮기는 함수
hanoi(k, from, to, spare)
    if k == 1
        move from into to
    else
        // k-1개의 원반을 from에서 spare로 옮긴다
        hanoi(k-1, from, spare, to)
        // 가장 아래 남은 원반 하나를 from에서 to로 옮긴다
        hanoi(1, from, to, spare)
        // 다시 k-1개의 원반을 spare에서 to로 옮긴다
        hanoi(k-1, spare, to, from)

재귀호출

  • 예) 메뉴 고르기
    • 주어진 예산범위 내에서 맛의 만족도 최대화 하기
      • 메뉴
        • 짜장면 - 가격: 5000원, 만족도 6점
        • 짬뽕 - 가격: 6000원, 만족도 7점
        • 탕수육 - 가격: 15000원, 만족도 9점
        • 깐풍기 - 가격: 17000원, 만족도 10점
      • 30,000원 내에서 같은 메뉴를 두 번 고르지 않고
        만족도를 최대화 하는 방법은?

재귀호출

  • 예) 메뉴 고르기
int N;
int MAX_N = 4;
int point[MAX_N];    // 만족도
int price[MAX_N];    // 가격
int max_point;    // 최대 만족도
int max_price = 30000;

int select(int i, int pr, int po) {
    if (pr > max_price) return; // 최대 가격을 넘으면 종료
    if (i == N) { // 마지막 원소까지 다 확인한 경우
        if (max_point < po) max_point = po; // 최대치 갱신
    } else {
        // i번째 메뉴를 선택하는 경우
        select(i + 1, pr + price[i], po + point[i]);

        // i번째 메뉴를 선택하지 않는 경우
        select(i + 1, pr, po);
    }
}
select(0, 0, 0);

재귀호출

  • 메뉴 고르기 = 집합의 원소 고르기 = 모든 경우의 수 구하기
    • { a, b, c, d, e, f } N 개의 원소를 가진 집합에서
      원소를 고르는 모든 경우를 구하라
    • 조합에서 조건에 부합하는 모든 경우를 구할 때 응용 가능
  • 예산 제한, 중복 제한 = 경우의 수 줄이기 = 백트래킹
    • N 개의 원소를 가진 집합에서 다음을 만족하는 모든 경우를 구하라

재귀호출

  • 재귀적 구현은 사람의 논리적 사고에 가장 가깝다
    • 루프로 구현하는 것보다 편하다고(?) 한다.
  • 깊이우선탐색(DFS) 이 가장 대표적인 재귀호출방법
  • 하지만 루프 구현보다 보통 리소스와 시간을 더 많이 소모한다.
    • 함수 호출로 인한 스택 사용 & 오버플로
  • 리턴 조건은 많이 추가할수록 좋다.
  • 문제에 따라서 시간내에 재귀로 풀 수 없는 문제들이 존재

분할정복

Divide and Conquer

분할정복

  • 주어진 문제를 더 작은 문제로 나누어 푸는 방법
  • 문제를 더 이상 나누지 않고 풀 수 있을 때 까지 나눈다
  • 부분문제의 답을 이용하여 원래 문제의 답을 구한다

분할정복? DP?

  • 분할정복과 DP의 큰 차이점은 중복호출 여부이다.
    • 분할정복은 중복호출을 하지 않는 경우를 말한다.
    • DP는 중복호출이 일어나 메모이제이션이 필요로 하는 경우를 말한다.

분할정복 요소

  • 분할(divide)
    • 문제를 더 작은 여러개의 부분 문제로 나눔
  • 병합(merge)
    • 부분 문제의 답에서 부터 원래 문제의 답을 유도
  • 기저 케이스(base case)
    • 더 이상 나누지 않고 풀 수 있는 문제

분할정복이 사용가능한 때

  • 분할 정복이 효율적인 문제
  • 문제를 동일한 형태의 부분 문제로 나눌 수 있는 경우
  • 부분 문제들이 서로 겹치지 않는 경우
  • 부분 문제의 답으로 부터 원래 문제의 해를 구할 수 있는 경우
  • 부분 문제들 중 일부분만 풀어도 되는 경우

분할정복 구현 형태

divideAndConquer(problem)
    if 풀 수 있을 만큼 작다면
        - 해당 범위를 풀고 값을 리턴 : base case
    else
        - 문제 구간을 나눈다.
        - 나눈 구간으로 재귀호출을 한다.  : divide
        - 각각 나눈 구간의 결과를 합친다. : merge
        - 합친 결과에서 값을 도출한다.
        - 값을 리턴한다.

N^P 구하기

const int MOD = 1000000007;

// calculate (n^p) % MOD in O(p)
int pow(int n, int p) {
    int ans = 1;
    for (int i = 0; i < p; ++i) {
        ans = (ans * n) % MOD;
    }
    return ans;
}
  • N을 P번 곱해서 구하기

분할정복으로 N^P 구하기

  • N^M * N^M = N^2M 성질을 이용한다.
    • base case : 1 if P == 0
    • divide
      • N^(P/2) * N^(P/2) if P is even
      • N^(P/2) * N^(P/2) * N if P is odd

분할정복으로 N^P 구하기

const int MOD = 1000000007;

// calculate (n^p) % MOD in O(log p)
int pow(int n, int p) {
    if (p == 0) {
        return 1;
    } else {
        int res = pow(n, p / 2);
        int ans = (res * res) % MOD;
        if (p % 2 == 1) {
            ans = (ans * n) % MOD;
        }
        return ans;
    }
}

병합정렬

Merge Sort

병합정렬

  • 구현하기 쉬운 대표적인 정렬
  • 최악의 경우에도 O(NlgN) 복잡도를 가짐
  • N만큼의 버퍼공간이 추가로 필요하다.
    • 병합용도로 사용
  • 분할 정복으로 구현

병합정렬

병합정렬

  1. 구간을 1/2로 쪼갠다.
    • 구간이 1또는 2가 될때까지 계속 쪼갬
  2. 쪼갰던 구간을 Ordering 을 거쳐 합친다.

병합정렬

sort(start, end) {
    if start == end
        return
    if start + 1 == end and a[start] > a[end]
        swap(a[start], a[end])
        return

    mid = (start + end) / 2
    sort(start, mid)
    sort(mid + 1, end)
    merge(start, end)
}
  • Sort 함수 구현

병합정렬

merge(start, end) {
    mid = (start + end) / 2
    i = start, j = mid + 1, k = 0
    
    while i <= mid && j <= end
        if a[i] <= a[j]
            b[k++] = a[i++]
        else
            b[k++] = a[j++]
    
    while i <= mid
        b[k++] = a[i++]
    while j <= end
        b[k++] = a[j++]

    for i = start to i <= end
        a[i] = b[i - start]
}
  • Merge 함수 구현

이진탐색

Binary Search

이진탐색

  • 정렬된 구조에서 목적값의 위치를 찾는 방법
  • 탐색 범위를 반으로 줄여가면서 찾는다
  • 분할 정복의 한 갈래
    • N/2 로 쪼개 둘 중 하나만 호출한다

이진탐색

  • 탐색 구간 내에서 값이 정렬되어 있는 경우
  • ​​상한과 하한을 정해서 주어진 값이 최적이 될 때까지 분할해 확인한다.

이진탐색 구현

while (lower_bound <= upper_bound) {
    int mid = (lower_bound + upper_bound) / 2;
    if (test(mid) == true) {
        answer = mid;
        upper_bound = mid - 1;
    } else {
        lower_bound = mid + 1;
    }
}

이진탐색 구현시 유의사항

  • 나누어야 할 요소가 정렬되어 있는가?
  • 상한과 하한은 무엇으로 정할 것인가?
    • 얻고자 하는 값의 최대/최소가 상한/하한이다.
    • 예측한 결과가 나올 수 있어야 한다.
    • 속도를 최대한 단축시킬 수 있어야 한다.
  • 상한 또는 하한을 변경하는 조건은 어떤 것인가?
    • 크거나, 크거나 같거나, 작거나, 작거나 같거나
  • 후보값(찾으려는값)을 언제 어떤 조건으로 갱신할 것인가?
    • 상한을 변경할때? 하한을 변경할때?

최적화 문제와 결정 문제

  • 어떤 조건을 만족하는 요소 K가 나열되어 있고
    그 중 가장 작거나 큰 K를 구하는 거라면(최적화)
    선택한 K를 넣었을 때의 결과를 기준으로 이진탐색이 가능하다.

 

 

  • 즉, 최적화 문제는 결정 문제로 바꿔서 풀 수 있다.

최적화 문제와 결정 문제

  • 최적화 문제
    • 조건을 만족하는 최소의 K를 구하라

 

 

  • 결정 문제
    • K일때 조건을 만족하는가?
    • K+1일때 조건을 만족하는가?
      ...

최적화 문제와 결정 문제

  • 최적화 문제
    • 일을 마칠 수 있는 최소 시간을 구하라

 

 

  • 결정 문제
    • K분만에 일을 마칠 수 있는가?
    • K-1분만에 일을 마칠 수 있는가?
      ...

결정 문제로 바꿔 풀기

  • 최적화 문제가
    • 가능한 K의 범위 내에서 정렬된 구조일 때
      • x 보다 작으면 모두 불가능
      • x 이상이면 모두 가능
    • 문제를 K에 대한 결정문제로 바꾸고
    • K에 대해 이진 탐색하여 x를 찾는다.
    • 초기 상한과 하한을 정할 때 적합한지 확인

그래프

Graph

그래프

  • 대상(object) 사이의 관계(relation)를 나타내는 자료구조
  • 대상 -> 정점(vertex or node)
  • 관계 -> 간선(edge)
  • 하나의 정점에 연결된 간선의 갯수 -> 차수(degree)

그래프로 모델링 하기

  • 친구 사이 모델링
    • 아이유와 유인나는 친구
    • 아이유와 장기하는 친구
    • 장기하와 양평이형은 친구
    • 장기하와 유재석은 친구
    • 아이유와 유재석은 친구
    • 유재석과 박명수는 친구
    • 박명수와 아이유는 친구

그래프로 모델링 하기

아이유

장기하

박명수

유재석

양평이형

유인나

그래프로 모델링 하기

  • 유인나와 양평이 형은 몇 단계를 건너서 아는 사이?
    • 유인나 - 아이유 - 장기하 - 양평이형
      • 3단계

그래프로 표현

  • 인접 행렬
    • 그래프를 행렬로 표현하는 방법
    • 정점의 갯수가 N개 이면 N*N 행렬을 사용
    • i번째 정점과 j번째 정점의 관계를 G[i][j]에 저장
    • 문제에서 주어지는 번호대로 저장
      • 배열이라고 0부터 저장하면 혼란함
    • 그래프에서 간선의 갯수가 따로 주어지지 않을 경우
      최대갯수는 V^2 이다.

그래프로 표현

  • 친구 그래프 인접행렬로 나타내기
        1 2 3 4 5 6
아이유 1 0 1 1 1 1 0
유재석 2 1 0 0 1 1 0
유인나 3 1 0 0 0 0 0 
장기하 4 1 1 0 0 0 1
박명수 5 1 1 0 0 0 0
양평형 6 0 0 0 1 0 0

그래프로 표현

  • 아이유와 장기하가 친구?
    • G[1][4] = 1 : 친구
  • 박명수와 장기하가 친구?
    • G[5][4] = 0 : 아님
        1 2 3 4 5 6
아이유 1 0 1 1 1 1 0
유재석 2 1 0 0 1 1 0
유인나 3 1 0 0 0 0 0 
장기하 4 1 1 0 0 0 1
박명수 5 1 1 0 0 0 0
양평형 6 0 0 0 1 0 0

그래프로 표현

int V; // 정점의 수
int E; // 간선의 수
int G[MAX_V + 1][MAX_V + 1]; // 인접행렬


scanf("%d", &V);
scanf("%d", &E);
for (int i = 0; i < E; ++i) {
    int u, v;
    scanf("%d%d", &u, &v);
    G[u][v] = 1; // 정점 u와 v는 연결
    G[v][u] = 1; // 정점 v와 u는 연결
}

그래프로 모델링하기 - 도로망

서울

인천

천안

대전

대구

부산

경주

전주

광주

여수

50

60

95

48

42

63

45

44

60

78

84

127

108

그래프로 모델링하기 - 도로망

     1   2   3   4   5   6   7   8   9  10
 1   0  50  60  -1  -1  -1  -1  -1  -1  -1
 2  50   0  -1  -1  -1  -1  -1  -1  -1  -1
 3  60  -1   0  95  -1  42  -1  -1  -1  -1
 4  -1  -1  95   0  48  -1  -1  -1  -1  -1
 5  -1  -1  -1  48   0  -1 108  -1  -1  -1
 6  -1  -1  42  -1  -1   0  -1  63  -1  -1  
 7  -1  -1  -1  -1 108  -1   0  84  -1 127
 8  -1  -1  -1  -1  -1  63  84   0  45  60
 9  -1  -1  -1  -1  -1  -1  -1  45   0  44
10  -1  -1  -1  -1  -1  -1 127  60  44   0

1: 서울, 2: 인천, 3: 천안, 4: 전주, 5: 광주
6: 대전, 7: 여수, 8: 대구, 9: 경주, 10: 부산

그래프로 모델링하기 - 도로망

  • 가중치 있는 그래프
int V; // 정점의 수
int E; // 간선의 수
int G[MAX_V + 1][MAX_V + 1]; // 인접행렬


scanf("%d", &V);
scanf("%d", &E);

// 인접행렬 초기화
for (int i = 0; i < V; ++i) {
    for (int j = 0; j < V; ++j) {
        G[i][j] = -1;
    }
    G[i][i] = 0;
}

// 간선을 입력 받아 인접행렬을 채운다
for (int i = 0; i < E; ++i) {
    int u, v, w;
    scanf("%d%d%d", &u, &v, &w);
    G[u][v] = w;
    G[v][u] = w;
}

그래프 공간복잡도

  • 인접행렬
    • 간선 정보를 행렬에 저장
    • 2차원 배열 이용
    • O(N^2)
  • 인접 리스트
    • 정점과 연결된 간선들을 리스트로 연결
    • 링크드 리스트 이용
    • O(E)
  • 간선 리스트
    • 간선을 배열에 순서대로 나열
    • 1차원 배열, 정렬, 구간합 이용
    • O(V+E)

깊이우선탐색

DFS

DFS

  • Depth First Search
  • 길이 있는 한 계속 따라 감
  • 막다른 길이면 돌아서 나오기

DFS 예시

A

B

C

E

D

F

G

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A
  • 종료 순서 :

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B
  • 종료 순서 :

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D
  • 종료 순서 :

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E
  • 종료 순서 :

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C
  • 종료 순서 :

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C
  • 종료 순서 : C

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G
  • 종료 순서 : C

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G
  • 종료 순서 : C G

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G
  • 종료 순서 : C G E

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G F
  • 종료 순서 : C G E

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G F
  • 종료 순서 : C G E F

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G F
  • 종료 순서 : C G E F D

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G F
  • 종료 순서 : C G E F D B

DFS 예시

A

B

C

E

D

F

G

  • 방문 순서 : A B D E C G F
  • 종료 순서 : C G E F D B A

DFS 예시

  • DFS의 구현은 보통 재귀함수로 한다.
    • 구현이 BFS보다 쉽다.
  • 크지 않은 조건의 경우의 수를 고려할 때 적합

DFS 구현 - 인접행렬

bool visited[MAX_N + 1];

void DFS(int u) {
    // 이미 방문했는지 검사
    if (visited[u]) {
        return;
    }
    
    // u번째 정점을 지금 방문함
    visited[u] = true;
    printf("%d\n", u);

    // 인접한 정점을 방문
    for (int v = 1; v <= N; ++v) {
        if (v == u) continue; // 자신은 건너뜀
        if (A[u][v]) {
            DFS(v);
        }
    }
}

2차원 좌표계에서 DFS하기

  • 2차원 좌표로 주어졌을 때 DFS를 하는 경우
    • 지도, 미로, 체스판, 장기 등
  • 임의의 좌표(x,y)에서 상하좌우로 이동가능하다면
    • 배열에서 dx, dy 처리하기 방식으로 총 4번의 재귀호출
  • 특정 좌표까지 경우의 수라든지 도달 여부등을 확인할 때 사용 가능
  • 최단거리 문제에서는 부적절함(시간초과 발생)

2차원 좌표계에서 DFS하기

int Y, X;
map[MAX_ROW + 1][MAX_COL + 1];
visited[MAX_ROW + 1][MAX_COL + 1];
// 상 > 하 > 좌 > 우
int dx[] = { 0, 0, -1, 1 };
int dy[] = { -1, 1, 0, 0 };

void dfs(int y, int x) {
    // 지도의 경계를 벗어나는지 검사
    if (y < 0 || y >= Y || x < 0 || x >= X) {
        return;
    }
    
    // 이미 방문했는지 검사
    if (visited[y][x]) {
        return;
    }

    // (y, x)를 방문
    visited[y][x] = true;
    printf("%d %d\n", y, x);

    for(int i = 0; i < 4; i++) {
        dfs(y + dy[i], x + dx[i]);
    }
}

너비우선탐색

BFS

BFS

  • Breadth First Search
  • 시작점에서 가까운 곳부터 차례대로 방문한다.

BFS 예시

  • 방문 순서
  • 방문 할 순서

A

B

C

E

D

F

G

BFS 예시

  • 방문 순서
  • 방문 할 순서 : A

A

B

C

E

D

F

G

1

BFS 예시

  • 방문 순서 : A
  • 방문 할 순서 : B C

A

B

C

E

D

F

G

1

2

2

BFS 예시

  • 방문 순서 : A B
  • 방문 할 순서 : C D E

A

B

C

E

D

F

G

1

2

3

2

3

BFS 예시

  • 방문 순서 : A B C
  • 방문 할 순서 : D E

A

B

C

E

D

F

G

1

2

3

2

3

BFS 예시

  • 방문 순서 : A B C D
  • 방문 할 순서 : E F

A

B

C

E

D

F

G

1

2

3

2

3

4

BFS 예시

  • 방문 순서 : A B C D E
  • 방문 할 순서 : F G

A

B

C

E

D

F

G

1

2

3

2

3

4

4

BFS 예시

  • 방문 순서 : A B C D E F
  • 방문 할 순서 : G

A

B

C

E

D

F

G

1

2

3

2

3

4

4

BFS 예시

  • 방문 순서 : A B C D E F G
  • 방문 할 순서 : 

A

B

C

E

D

F

G

1

2

3

2

3

4

4

BFS 예시

  • 방문 순서 : A B C D E F G
  • 방문 할 순서 : 

A

B

C

E

D

F

G

1

2

3

2

3

4

4

BFS 예시

  • 방문 순서 : A B C D E F G
  • 방문 할 순서
    • 큐로 구현

BFS - 구현

push(start); // 시작 지점을 큐에 넣음
int step = 0;
while (!queueIsEmpty()) {
    step++;    // 시작정점에서의 거리
    // 현재 큐에 들어있는 모든 노드는 같은 거리에 있다.
    int queue_size = size();   
    for (int i = 0; i < queue_size; ++i) {
        int u = pop();
        printf("%d\n", u);
        for (int v = 1; v <= N; ++v) {
            if (u != v && G[u][v] && visited[v] == false) {
                push(v);
                visited[v] = true;
            }
        }
    }
}

BFS - 구현

dy[] = { 1, 0, -1, 0 };
dx[] = { 0, 1, 0, -1 };

push(startPoint);
int step = 0;
while (!queueIsEmpty()) {
    step++;
    int queue_size = queueSize();
    for (int i = 0; i < queue_size; ++i) {
        Point p = pop();
        printf("%d %d\n", p.x, p.y);
        for (int d = 0; d < 4; ++d) {
            Point next;
            next.x = p.x + dx[d];
            next.y = p.y + dy[d];
            if(visited[next.y][next.x] == false) {
                push(next);
                visited[next.y][next.x] = true;
            }
        }
    }
}
  • 2차원 좌표계일 경우

DFS, BFS의 시간복잡도

  • DFS와 BFS 에서 주어지는 변수는 정점과 간선
    • 즉, 시간복잡도는 정점 V의 개수와 간선 E의 개수로 복합적으로 표현됨
  • 목적에 따라 다양한 그래프 알고리즘이 존재하며
    시간복잡도도 다름

최단경로

Shortest Path

최단 거리

  • 한 정점에서 다른 정점으로 가는 최단 거리를 구하는 문제
  • 네비게이션

최단 거리

  • 간선의 가중치가 모두 1인 경우
    • BFS를 이용하여 구할 수 있다.
    • 아까 소스에서 step 이 바로 시작정점에서부터 거리

최단 거리

  • 간선의 가중치가 다른 경우
    • 시작정점에서 특정 목표 정점까지의 최단거리
      • 다익스트라 알고리즘
      • 벨만포드 알고리즘 : 간선에 음수가 있을 경우
    • 모든 쌍에 대해 최단거리
      • 플로이드 알고리즘
      • 시간복잡도 : O(V^3)