Problem Solving
and
Algorithm

Problem Solving

• 주어진 문제의 해결방법을 찾는 과정
• 프로그래밍을 이용한 문제 해결
  • ​잘 정의된 문제를 해결
  • 프로그래밍 언어로 프로그래밍 된 절차(알고리즘)에 따라 문제를 해결

알고리즘

• 어떠한 기능을 수행하기 위한 명령의 모임​​
  • 유한한 명령으로 구성된다.
  • 유한한 동작 후 종료한다.
  • 올바른 답을 출력한다.
  • 모든 명령은 엄밀히 이행된다.
    • 각 단위연산은 기계적으로 수행

이것을 왜 하나?

• 생각하는 훈련
• 잘 정의 되지 않은 문제를 잘 해결 하려면
  • 잘 정의되어 있는 문제정도는 잘 풀 수 있어야..

훈련하기

1. 알려진 알고리즘의 이해
   • 이론, 구현, 적용 예
2. 관련된 문제를 풀어보기
3. 잘 모르겠으면 질문하기
   • 단 아주 열심히 생각해 본 후에도 모르겠는 경우
4. 시간을 가진 후 다시 풀어보기
5. 완전히 익숙해 질 때까지 무한 반복

문제 해결 훈련에 임하는 자세

• 잘 정의된 문제의 해결 방안
  • 이미 잘 알려진 경우가 대부분
    • 새로 발명할 필요가 없다 (그 분야 연구자가 아닌 이상..)
  • 이미 잘 알려진 그 방법을 내 것으로 만들기

어제는 못 풀었던 문제를 오늘은 풀 수 있으면 성공

파인만의 문제해결 알고리즘

1. 문제를 적는다.
2. 골돌히 생각한다.
3. 답을 적는다.

파인만의 문제해결 알고리즘

1. 문제를 적는다.
2. 골돌히 생각한다.
3. 답을 적는다.

가장 중요

Big-O Notation

시간 복잡도 분석

• 주어진 입력에 대한 알고리즘의 수행 시간을 분석
  • Big-O 표기법으로 표현
  • 문제를 해결하기 위한 전체 단위 연산의 갯수
  • 최악의 경우(worst case)를 고려

시간 복잡도 분석 예

• 1부터 n 까지 합을 구하기 1

int sumToN(int n) {
    int sum = 0;
    for (int i = 1; i <= n; ++i) {
        sum += i;
    }
    return sum;
}

• 단위 연산 (sum += i) 가 n번 실행
  • O(n)

시간 복잡도 분석 예

• 1부터 n 까지 합을 구하기 2

int sumToN(int n) {
    int sum = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            sum += 1;
        }
    }
    return sum;
}

• i (1 ~ n)에 대해 단위 연산 (sum += 1) 가 i번 실행
  • O(n^2)

시간 복잡도 분석 예

• 1부터 n 까지 합을 구하기 3

int sumToN(int n) {
    return n * (n + 1) / 2
}

• 입력(n)에 상관없이 하나의 단위 연산 수행
  • O(1)

Big-O notation

• 전달인자가 무한대로 커질 때 함수값의 변화양상을 분석하기 위한 수학적 도구
• 알고리즘에서 Big-O 표기법의 의미
  • 큰 입력에 대해 알고리즘이 얼마나 빨리 종료하는지 나타냄
    • n이 충분히 큰 경우, O(n) 알고리즘이 O(n^2) 알고리즘보다 빨리 종료한다

다양한 Big-O

• O(1)
• O(log n)
• O(n)
• O(n log n)
• O(n^2)
• O(n^3)
• O(2^n)
• O(n!)

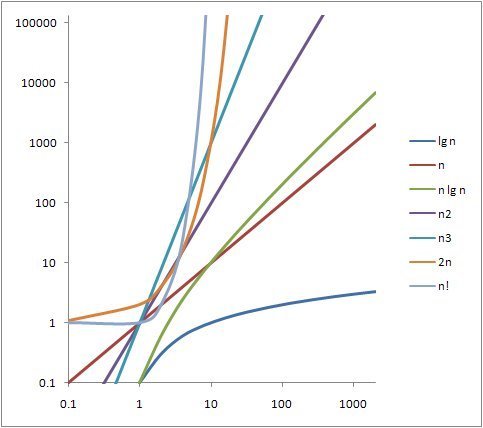
다양한 Big-O

• O(1)
• O(log n)
• O(n)
• O(n log n)
• O(n^2)
• O(n^3)
• O(2^n)
• O(n!)

입력 크기에 따라 알고리즘 결정하기

1. 생각한 알고리즘을 Big-O 표기법으로 나타낸다.
2. 입력 크기를 대입한다.
3. 값이 수천만~1억 이하인지 확인한다. (1초 기준)
4. 값이 넘어가면 더 좋은 알고리즘을 생각한다.

입력 크기에 따라 알고리즘 결정하기

• 예를 들어, 인풋 크기가..
  • 테스트 케이스 T=50, N <= 500
• O(n^3) 알고리즘이 가능할까?
  • n^3 = 500 ^3 = 125000000 너무커서 안될듯

입력 크기에 따라 알고리즘 결정하기

• 예를 들어, 인풋 크기가..
  • 테스트 케이스 T=50, N <= 500
• O(n^2) 알고리즘은 가능할까?
  • n^2 = 500^2 = 250000
  • 테스트 케이스가 50개이므로 250000*50 = 12500000
  • 가능할듯!!!

Problem Solving
기초 전략

단계 1 - 문제를 적는다

• 문제를 정확히 이해하는 것이 중요
• 문제를 이해했으면 자신의 표현으로 다시 정리한다
• 문제의 입력크기의 상한에 유의

단계 2 - 연필과 종이로 풀기

• 연필과 종이를 이용하여 문제를 풀어본다
  • 일반적인 케이스에 대해 적용 가능한 풀이법 
  • 풀이 과정을 절차적 단계로 분해 가능
    • 머릿속의 복잡한 과정을 풀어내는 훈련

단계 2 - 연필과 종이로 풀기

• 예) 16 과 24의 최대공약수를 구하라!
  • 음........ 8이군!!!!!

단계 2 - 연필과 종이로 풀기

• 예) 16 과 24의 최대공약수를 구하라!
  • 음........ 8이군!!!!!
    • 여기서 그치면 알고리즘이 아님
    • 모든 계산 단계에서
      • 직관적 요소를을 배제
      • 기계적 계산요소로만 구성해야 함

단계 2 - 연필과 종이로 풀기

• 예) 16 과 24의 최대공약수를 구하라!
  • 공약수는 두 수를 모두 나누는 정수
  • 1보다는 같거나 크고 두 수보다는 같거나 작은 수
  • 그럼 1부터 16까지 차근차근 다 나눠보자

단계 2 - 연필과 종이로 풀기

• 예) 16 과 24의 최대공약수를 구하라! 
  • 그럼 1부터 16까지 차근차근 다 나눠보자
    • 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
    • ​​8이 정답이구나!!

단계 3 - 알고리즘 구성하기

• 연필과 종이로 문제를 해결한 과정을 알고리즘으로 구성
• 예) 두 수 a와 b의 최대공약수를 구하라!
  1. let c = min(a, b)​
  2. for any k in range [1, c]
     • find maximum k that divides both a and b

단계 4 - 알고리즘 시간 복잡도 분석

• 앞 단계에서 구성한 알고리즘의 시간 복잡도를 분석
• 최대 입력 사이즈를 대입하여 예상 수행 시간을 가늠
  • 비효율적이면 더 효율적인 방법을 생각

단계 5 - 구현

• 알고리즘을 프로그래밍 언어로 옮겨 적기

int gcd(int a, int b) {
    int great_common_divisor = 1;
    for (int k = 1; k <= a && k <= b; ++k) {
        if (a % k == 0 && b % k == 0) {
            great_common_divisor = k;
        }
    }
    return great_common_divisor;
}

참고: 유클리드 알고리즘이 훨씬 효율적입니다

단계 6 - 테스트

• 구현한 코드를 테스트
  • 테스트 결과에 따라 다른 전략
    • 테스트 가이드 참고

팁

• 문제를 정확하게 이해하는 것이 필수
• 연필과 종이로 풀 때 시간 복잡도를 고려
• 숙련도와 문제 난이도에 따라 2, 3, 4, 5 단계를 한 번에 할 수 있게 됨

코딩 및 테스트 가이드
C/C++

코딩 가이드

입력

• scanf() 사용하기

int n;
char a;
char s[100];

scanf("%d", &n); // 숫자 입력 받기
scanf("%c", &a); // 문자 입력 받기
scanf("%s", s); // 문자열 입력 받기

int x, y;
scanf("%d%d", &x, &y); // 숫자 2개 입력 받기

int age;
char name[100];
scanf("%d%s", &age, name); // 나이(숫자)와 이름(문자열) 입력 받기

출력

• printf() 사용하기

printf("Hello world!\n"); // 개행문자는 '\n'

printf("%d + %d = %d\n", 1, 2, 1 + 2); // 1 + 2 = 3

printf("%d", x); // int 변수값 출력하기

printf("%s", s); // 문자열 변수값 출력하기

for (int tc = 1; tc <= TC; ++tc) {
    printf("Case #%d: %d\n", solve());
}

입출력

• 입출력은 번갈아 해도 상관없음!!

int main() {
    int TC;
    scanf("%d", &TC);
    for (int tc = 1; tc <= TC; ++tc) {
        int x;
        scanf("%d", &x);
        printf("Case #%d: %d\n", tc, x * x);
    }
    return 0;
}
    

배열 선언

const int MAX_N = 1000;

int N;
int A[MAX_N + 1][MAX_N + 1];

int main() {
    ...
    return 0;
}

• 큰 배열은 전역에서 선언
  • 동적 할당 하지 말고 전역에서 정적 할당
  • 인풋으로 주어질 수 있는 최대 크기로 선언
• 배열 크기에 여유를 주기

변수 선언

• 한 변수는 한 가지 용도로만 사용하기
  • 한 변수를 두 가지 이상 용도로 재사용 하지 말자
• 변수 이름을 의미 있는 것으로
  • a, b, c, d, ... 이런식으로 이름 지으면 나중에 햇갈림

초기화

• 변수 초기화
  • 특히 전역 변수
• 동적할당한 메모리 해제

프로덕트를 생산하는 것이 아님

• 실제 프로덕트를 생산하는 것이라면
  • 훌륭한 디자인 (OOP...)
  • 재사용 가능한 자료구조
  • 예외 처리
  • Readability, maintainability, ...
• 그러나 단지 문제 해결 연습을 위한 것이라면
  • 위의 것들을 과감히 포기한다!

테스트 가이드

테스트에 임하는 자세

• 주어진 샘플 테스트 맞았다고 방심하지 금물!
  • 실제 환경은 훨씬 다양한 케이스가 있다. 
• 스스로 테스트 케이스를 작성
• 디버그는 눈으로

테스트 케이스 만들기 1

• 손과 종이로 풀 수 있는 최대한 크고 복잡한 케이스
  • 크게, 복잡하게, 여러개 만들기
  • 다양한 인풋에 대해 올바르게 동작하는지 확인

테스트 케이스 만들기 2

• 최대 사이즈 케이스
  • 최대 입력 사이즈에 해당하는 케이스 작성
    • 랜덤 함수 이용
    • 모두 같은 값
    • 1,2,3,4, ...
  • 최대 사이즈에서 시간초과, 메모리 초과 확인용

테스트 케이스 만들기 3

• 최소 사이즈 케이스
  • 최소 입력 사이즈에 해당하는 케이스 작성
  • 최소 입력에서 코너 발생 가능성
    • 0
    • 1

오답에 대처하는 자세 1

• 오답(WA, Wrong Answer)
  • 알고리즘 검증
    • 단위 검증
  • 버퍼 오버플로우 확인
  • ​테스트 케이스 작성하여 추가 테스트
  • 코너 케이스 검증

오답에 대처하는 자세 2

• 시간 초과(TLE, Time Limit Exceeded)
  • 무한루프 가능성 검사
  • 입력 덜 받았는지 검사
  • ​알고리즘 개선
    • ​Big-O 단위 더 좋은 알고리즘으로 갈 것!!
    • 코드 최적화는 도움 안 됨

오답에 대처하는 자세 3

• 런타임 오류(Runtime Error)
  • 세그멘테이션 폴트 확인
    • 포인터 참조 오류
    • 버퍼 오버플로우
    • 스택 오버플로우

디버그하기

1. 코드를 눈으로 보면서 디버그 하기
2. Trace 출력하기
3. 디버거 이용하기

데이터 표현
C++

Primitive Types in C++

• 정수형
• 실수형
• 문자
• 참/거짓

정수 타입 1

• 정수를 표현하기 위한 데이터 타입
  • int
    • 부호 있는 32비트 정수
    • -2^31 ~ 2^31-1(약 -20억 ~ 20억)
  • unsinged int
    • 부호 없는 32비트 정수
    • 0 ~ 2^32 - 1 (약 0 ~ 40억) 

정수 타입 2

• 정수를 표현하기 위한 데이터 타입
  • short
    • 16비트
    • -32768 ~ 32768 
  • long long
    • 64 비트 
    • -9 * 10^18 ~ 9 * 10^18

실수 타입

• 실수를 표현하기 위한 데이터 타입
  • float, double
  • 부동 소수점 표현 방법을 사용한다
  • 실수 오차
    • 64비트로 표현(double)하므로 모든 실수를 정확하게 표현할 수는 없다.
    • 계산시 오차가 누적될 수 있다. 

문자 타입 1

• 문자를 표현하기 위한 데이터 타입
  • char
  • 사실은 8비트 정수형
  • 정수 <-> 문자 코드 (ASCII)
    • '0' = 48
    • 'A' = 65
    • 'a' = 97

문자 타입 2

• 사실은 8비트 정수형 이므로 정수 연산을 할 수 있다
  • '0' + 1 = '1'
  • 'A' + 3 = 'D'
  • 'G' + 32 = 'g'
  • 'p' - 32 = 'P'

부울 타입

• 참, 거짓을 나타내기 위한 타입
  • bool
  • true or false

오버플로우

• 연산시 범위를 벗어나는 경우
• ​연산 결과의 하위 비트만 취한다

int a = 2147483647; // maximum value of integer
int b = a + 1; // b = -2147483648 not 2147483648
int c = a + 2; // c = -2147483647

형 변환

• 자료형을 바꾸는 것
• 데이터 표현 범위가 큰 타입에서 작은 타입으로 형 변환 할 때 데이터 손실 발생 유의
  • 오버플로우 발생

int a = 32768;
long long b = a; // b = 32768
short c = a;     // c = -32768

숫자인 문자를 숫자로

• 아스키 코드표를 보면...
  • '0': 48
  • '1': 49
  • '2': 50 ...
• 따라서 숫자 문자에서 '0'을 빼면 숫자가 된다

int asciiDigitToNumber(char x) {
    // x >= '0' && x <= '9'
    return x - '0';
}

char numberDigitToAscii(int x) {
    // x >= 0 && x <= 9
    return x + '0';
}

Array

• 배열
• 동일한 타입의 자료가 연속적으로 있는 것
• 인덱스를 이용하여 개별 요소에 접근
  • 인덱스는 0부터 시작

int a[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};

printf("%d\n", a[0]); // 1
printf("%d\n", a[1]); // 2

String

• 문자열
• 문자 타입의 자료가 연속적으로 있는 것
• 문자열은 끝은 널 문자(null, '\0')

  char a[] = { 'h', 'e', 'l', 'l', 'o', '\0' };
  char b[] = "world";

  printf("%s %s\n", a, b); // hello world

문자열의 길이

• 문자열의 처음 부터 널 문자 까지의 문자 갯수

int strlen(char* s) {
    int len = 0;
    while (s[len]) {
        len++;
    }
    return len;
}

소문자를 대문자로

• ASCII 코드 표를 보면 소문자가 대문자보다 32크다.
  • 'A': 65, 'a': 97
  • 'B': 66, 'b': 98
• 문자열의 각 문자를 보고 소문자이면 32를 빼면 대문자가 된다

void toCapitalCase(char* s) {
    for (int i = 0; s[i]; ++i) {
        if (s[i] >= 'a' && s[i] <= 'z') {
            s[i] -= 32;
        }
    }
}

void toLowerCase(char* s) {
    for (int i = 0; s[i]; ++i) {
        if (s[i] >= 'A' && s[i] <= 'Z') {
            s[i] += 32;
        }
    }
}

숫자 쪼개기

• 숫자가 주어졌을 때 한 자리씩 쪼개기
  • 숫자를 10으로 계속 나누면서 마지막 자리숫자를 보면 된다.

while (n > 0) {
    int k = n % 10;
    // do something with k
    ...
    n /= 10;
}

선형 자료구조

선형 자료구조

• 자료를 일자 형태로 저장하는 자료구조
  • 배열, 리스트, 스택, 큐 ...

배열

• 연속된 공간에 자료를 저장
• 맵: 인덱스(정수) -> 데이터
• 인덱스를 이용하여 배열의 임의의 요소에 빠르게 접근 가능 

배열 사용하기

• 데이터를 정수로 사상 할 수 있을때
  • ID, hash, 데이터 자체가 정수
  • 이 값을 배열의 인덱스로 사용
  • 배열에 데이터에 관한 추가정보를 저장
    • 데이터가 존재하는지?
    • 데이터가 몇 번 나타나는지?
    • 데이터를 방문한 적이 있는지?
    • ...

구간합

• 수열 A[0], A[1], A[2], ... , A[n] 에 대해서
• A[p], ... , A[q] 까지 합을 구하기

// O(n)
int sum(int A[], int p, int q) {
    int res = 0;
    for (int i = p; i <= q; ++i) {
        res += A[i];
    }
}

구간합

• S[k] = A[0] ... A[k - 1] 까지 합
  • S[0] = 0
  • S[k] = S[k - 1] + A[k - 1]
    • S[k + 1] = S[k] + A[k]
• A[p] + A[p + 1] + ... + A[q] 
  • S[q + 1] - S[p]

구간합

const int MAX_N = 10000;
int S[MAX_N + 1];

// O(n)
int suffixSum(int A[], int n) {
    S[0] = 0;
    for (int i = 0; i < n; ++i) {
        S[i + 1] = S[i] + A[i];
    }
}

// O(1)
int sum(int p, int q) {
    return S[q + 1] - S[p];
}

스택

• 자료를 쌓아 올림
• 한 쪽 방향에서만 자료가 들어가고 나오는 구조
  • First In Last Out
• 스택 연산
  • push
  • pop

배열 이용하여 스택 구현하기

const int MAX_STACK_SIZE = 1000;

int stack[MAX_STACK_SIZE + 1];
int stack_top;

void stackInit() {
    stack_top = 0;
}

int stackSize() {
    return stack_top;
}

bool stackIsEmpty() {
    return stack_top == 0;
}

void stackPush(int x) {
    stack[stack_top++] = x;
}

int stackPop() {
    return stack[--stack_top];
}

큐

• 줄서기
• 한 쪽에서 들어가고 반대쪽에서 나오는 구조
  • First In First Out
• 큐 연산
  • push
  • pop

배열을 이용하여 큐 구현

const int MAX_QUEUE_SIZE = 10000;

int queue[MAX_QUEUE_SIZE + 1];
int queue_head;
int queue_tail;

void queueInit() {
    queue_head = queue_tail = 0;
}

int queueSize() {
    return queue_tail - queue_head;
}

bool queueIsEmpty() {
    return queueSize() == 0;
}

void queuePush(int x) {
    queue[queue_tail++] = x;
}

int queuePop() {
    return queue[queue_head++];
}

정렬

정렬

• 데이터를 어떤 순서대로 재배치 하는 것

정렬 방법과 시간복잡도

• 비교 정렬
  • 두 요소의 대소를 비교해 자리를 바꾸는 방법
  • O(n^2) 정렬
    • 구현이 쉽다
    • 느리다 
  • O(n log n)
    • 구현이 어렵다
    • 빠르다

O(n^2) 정렬

• bubble, insertion, selection sort 등이 있다 

void bubbleSort(int A[], int len) {
    for (int i = 0; i < len; ++i) {
        for (int j = 1; j < len; ++j) {
            if (A[j - 1] > A[j]) {
                swap(A[j - 1], A[j]);
            }
        }
    }
}

카운팅 소트

• 모든 요소를 정수로 사상 가능하고 그 범위가 제한적일 때
• 각 숫자의 갯수를 카운팅 하여 정렬함

int count[MAX_N + 1];

int countSort(int A[], int len) {
    for (int i = 0; i < MAX_N; ++i) {
        count = 0;
    }
    for (int i = 0; i < len; ++i) {
        count[A[i]]++;
    }
    for (int v = 0, idx = 0; v <= MAX_VALUE; ++v) {
        for (int i = 0; i < count[v]; ++i) {
            A[idx++] = v;
        }
    }
}

Brute Force

Brute Force

• 문제에서 주어진 가능한 모든 경우를 확인하는 방법
• 모든 경우를 다 따져보기 때문에 가장 안전함
  • 놓치는 케이스가 없다.
• 모든 경우를 다 따져보기 때문에 느릴 수 있음
  • 시간 복잡도 분석이 필요

Why Brute Force

• 시간 복잡도 분석한 결과 충분히 여유가 있으면 이 방법을 추천
  • 가장 먼저  Brute force를 고려하자
  • Brute force로 풀 때 장점
    • 반례를 만날 가능성이 적다
    • 구현이 쉬운 경향이 있다

How Brute Force

• 모든 경우를 열거할 수 있는지 생각해본다
  • 루프를 돌거나 재귀호출을 하거나
• 각 경우에 대해 문제를 쉽게 풀 수 있는지 확인한다
• 시간복잡도 분석 필수
  • 시간복잡도 = 경우의 수 * 각 경우를 푸는 시간
  • 시간복잡도가 너무 크면
    • 일부 경우만 보고 풀 수 있는지 확인한다
    • n 배 이상 빨리 풀 수 있어야 의미가 있다

Brute Force 구현 방법

• 돌고 돌고 돌고...
  • 루프를 이용하여 모든 경우를 본다
• 들어가고 들어가고 들어가고
  • 재귀호출을 이용하여 모든 경우를 본다
• 찾고 찾고 찾고
  • 탐색을 이용하여 필요한 경우를 본다

Recursion

재귀 Recursion 

• 재귀적 구조
  • 부분이 전체와 닮아 있다
• 재귀함수
  • 자기 자신을 호출하는 함수
    • 동일 작업을 반복 수행

재귀와 귀납

• 재귀(Recursion)와 귀납(induction)의 관계
  • 귀납적으로 정의되는 것은 재귀적 성질을 갖는다
    • 자연수
    • 피보나치 수열
    • 각종 점화식으로 나타낼 수 있는 것

귀납적 정의 - 자연수 

• 귀납적으로 정의하기 예
  • 자연수
    • base case
      • 1
    • others
      • k 번째 자연수 = k - 1 번째 자연수 + 1

귀납적 정의 - 피보나치 수 

• 귀납적으로 정의하기 예
  • 피보나치 수
    • base case
      • f(0) = 0
      • f(1) = 1
    • others
      • f(k) = f(k-1) + f(k-2)

재귀함수로 구하기

• 귀납적 방법으로 정의되는 구조는 재귀함수로 구현할 수 있다
• 피보나치 수

int fib(int k) {
    // base cases
    if (k == 0) return 0;
    if (k == 1) return 1;
    
    // others
    return fib(k - 1) + fib(k - 2);
}

문제를 재귀적으로 풀기

• 문제가 재귀적으로 구성되는지 생각
  • 동형 반복
    • 같은 형태의 작업을 반복 수행
  • 종료조건
    • 재귀호출이 종료되는 조건

하노이 탑

• 한 기둥에 있는 원판들을 다른 원판으로 옮기는 게임
  • 한 번에 하나의 원판만 옮길 수 있다
  • 큰 원판이 작은 원판 위에 있을 수 없다

재귀적으로 하노이 탑 풀기

• k 층 탑을 A기둥에서 B기둥으로 옮기기
  • k가 1인 경우
    • 그냥 옮긴다
  • k가 1보다 큰 경우
    • k-1층 탑을 A에서 C로 옮긴다
    • k번째 원판을 A에서 B로 옮긴다
    • k-1층 탑을 C에서 B로 옮긴다

재귀적으로 하노이 탑 풀기

A

B

C

k-1

kth

재귀적으로 하노이 탑 풀기

A

B

C

k-1

kth

재귀적으로 하노이 탑 풀기

A

B

C

k-1

kth

재귀적으로 하노이 탑 풀기

A

B

C

k-1

kth

재귀적으로 하노이 탑 풀기

// k 개의 원반을 from에서 to로 옮기는 함수
hanoi(k, from, to, spare)
    if k == 1
        move from into to
    else
        // k-1개의 원반을 from에서 spare로 옮긴다
        hanoi(k-1, from, spare, to)
        // 가장 아래 남은 원반 하나를 from에서 to로 옮긴다
        hanoi(1, from, to, spare)
        // 다시 k-1개의 원반을 spare에서 to로 옮긴다
        hanoi(k-1, spare, to, from)

집합의 원소 선택하기

• 주어진 집합에서 원소를 적당히 고르는 문제
• 예) 주어진 예산범위 내에서 맛의 만족도 최대화 하기
  • 메뉴
    • 짜장면 - 가격: 5000원, 만족도 6점
    • 짬뽕 - 가격: 6000원, 만족도 7점
    • 탕수육 - 가격: 15000원, 만족도 9점
    • 깐풍기 - 가격: 17000원, 만족도 10점
  •  30000원으로 같은 메뉴를 두 번 고르지 않고 만족도 최대화 하는 방법은?

집합의 원소 선택하기

int N;
int S[MAX_N];
int max_value;

int dfs(int depth, int value) {
    if (depth == N) { // 마지막 원소까지 다 확인한 경우
        // 최대치 갱신
        if (max_value < value) {
            max_value = value;
        }
    } else {
        // depth번째 아이템을 선택하는 경우
        dfs(depth + 1, value + S[depth]);

        // depth번째 아이템을 선택하지 않는 경우
        dfs(depth + 1, value);
    }
}


dfs(0, 0);

Divide and Conquer

분할 정복

• 주어진 문제를 더 작은 문제로 나누어 푸는 방법
• 문제를 더 이상 나누지 않고 풀 수 있을 때 까지 나눈다
• 부분문제의 답을 이용하여 원래 문제의 답을 구한다

분할 정복 요소

• 분할(divide)
  • 문제를 더 작은 여러개의 부분 문제로 나눔
• 병합(merge)
  • 부분 문제의 답에서 부터 원래 문제의 답을 유도
• 기저 케이스(base case)
  • 더 이상 나누지 않고 풀 수 있는 문제

분할 정복을 언제 쓰나

• 분할 정복이 효율적인 문제
  • 문제를 동일한 형태의 부분 문제로 나눌 수 있는 경우
  • 부분 문제들이 서로 겹치지 않는 경우
  • 부분 문제의 답으로 부터 원래 문제의 해를 구할 수 있는 경우
  • 부분 문제들 중 일부분만 풀어도 되는 경우

분할 정복 뼈대

divideAndConquer(problem)
    if able to solve the problem
        solve it and return the answer
    else
        divide problem into subproblems
        solve each subproblems by recursive call
        merge answers of subproblems
        reduce answer for the problem
        return the answer

n^p 구하기

• n을 p번 곱해서 풀 수 있다

const int MOD = 1000000007;

// calculate (n^p) % MOD in O(p)
int pow(int n, int p) {
    int ans = 1;
    for (int i = 0; i < p; ++i) {
        ans = (ans * n) % MOD;
    }
    return ans;
}

분할 정복으로 n^p 구하기

• n^p
  • 1 if p == 0
  • n^(p/2) * n^(p/2) if p is even
  • n^(p/2) * n^(p/2) * n if p is odd

분할 정복으로 n^p 구하기

const int MOD = 1000000007;

// calculate (n^p) % MOD in O(log p)
int pow(int n, int p) {
    if (p == 0) {
        return 1;
    } else {
        int res = pow(n, p / 2);
        int ans = (res * res) % MOD;
        if (p % 2 == 1) {
            ans = (ans * n) % MOD;
        }
        return ans;
    }
}

Binary Search

이분 탐색 Binary Search

• 정렬된 구조에서 목적값의 위치를 찾는 방법
• 탐색 범위를 반으로 줄여가면서 찾는다
• 분할 정복의 한 갈래

이분 탐색을 할 수 있는 경우

• 탐색 구간 내에서 값이 정렬되어 있는 경우
  • 비내림차순
  • 비오름차순
  • ..., false, false, false, true, true, true, ...

이분 탐색 구현

while (lower_bound <= upper_bound) {
    int mid = (lower_bound + upper_bound) / 2;
    if (test(mid) == true) {
        answer = mid;
        upper_bound = mid - 1;
    } else {
        lower_bound = mid + 1;
    }
}

최적화 문제와 결정 문제

• 최적화 문제
  • 조건을 만족하는 최소의 k를 찾아라
• 결정문제
  • k일 때 조건을 만족 하는가?

최적화 문제와 결정 문제 예

• 최적화 문제
  • 일을 마칠 수 있는 최소 시간을 구하라
• 결정문제
  • k분만에 일을 마칠 수 있는가?

결정 문제로 바꿔 풀기

• 최적화 문제가
  • 가능한 k의 범위 내에서 정렬된 구조일 때
    • x 보다 작으면 모두 불가능
    • x 이상이면 모두 가능
  • 문제를 k에 대한 결정문제로 바꾸고
  • k에 대해 이분 탐색하여 x를 찾는다

Graph

그래프 Graph

• 대상(object) 사이의 관계(relation)를 나타내는 자료구조
  • 대상 -> 정점(vertex)
  • 관계 -> 간선(edge)

그래프로 모델링 하기

• 친구 사이 모델링
  • 아이유와 유인나는 친구
  • 아이유와 장기하는 친구
  • 장기하와 양평이형은 친구
  • 장기하와 유재석은 친구
  • 아이유와 유재석은 친구
  • 유재석과 박명수는 친구
  • 박명수와 아이유는 친구

그래프로 모델링 하기

아이유

장기하

박명수

유재석

양평이형

유인나

그래프로 모델링 하기

• 유인나와 양평이형은 몇 단계를 건너서 아는 사이?
  • 유인나 - 아이유 - 장기하 - 양평이형
  • 답: 3단계

그래프로 표현

• 인접 행렬
  • 그래프를 행렬로 표현하는 방법
  • 정점의 갯수가 n개 이면 n*n 행렬을 사용
  • i번째 정점과 j번째 정점의 관계를 A[i][j]에 저장

그래프로 표현

• 친구 그래프 인접행렬로 나타내기

       1 2 3 4 5 6
아이유 1 0 1 1 1 1 0
유재석 2 1 0 0 1 1 0
유인나 3 1 0 0 0 0 0 
장기하 4 1 1 0 0 0 1
박명수 5 1 1 0 0 0 0
양평형 6 0 0 0 1 0 0

그래프로 표현

• 아이유와 장기하가 친구?
  • A[1][4] = 1 -> 친구
• 박명수와 장기하가 친구?
  • A[5][4] = 0 -> 아님

       1 2 3 4 5 6
아이유 1 0 1 1 1 1 0
유재석 2 1 0 0 1 1 0
유인나 3 1 0 0 0 0 0 
장기하 4 1 1 0 0 0 1
박명수 5 1 1 0 0 0 0
양평형 6 0 0 0 1 0 0

그래프 표현 구현

int V; // 정점의 수
int E; // 간선의 수
int G[MAX_V + 1][MAX_V + 1]; // 인접행렬


scanf("%d", &V);
scanf("%d", &E);
for (int i = 0; i < E; ++i) {
    int u, v;
    scanf("%d%d", &u, &v);
    G[u][v] = 1; // 정점 u와 v는 연결
    G[v][u] = 1; // 정점 v와 u는 연결
}

그래프로 모델링하기 - 도로망

서울

인천

천안

대전

대구

부산

경주

전주

광주

여수

50

60

95

48

42

63

45

44

60

78

84

127

108

인접행렬 - 도로망

     1   2   3   4   5   6   7   8   9  10
 1   0  50  60  -1  -1  -1  -1  -1  -1  -1
 2  50   0  -1  -1  -1  -1  -1  -1  -1  -1
 3  60  -1   0  95  -1  42  -1  -1  -1  -1
 4  -1  -1  95   0  48  -1  -1  -1  -1  -1
 5  -1  -1  -1  48   0  -1 108  -1  -1  -1
 6  -1  -1  42  -1  -1   0  -1  63  -1  -1  
 7  -1  -1  -1  -1 108  -1   0  84  -1 127
 8  -1  -1  -1  -1  -1  63  84   0  45  60
 9  -1  -1  -1  -1  -1  -1  -1  45   0  44
10  -1  -1  -1  -1  -1  -1 127  60  44   0

1: 서울, 2: 인천, 3: 천안, 4: 전주, 5: 광주
6: 대전, 7: 여수, 8: 대구, 9: 경주, 10: 부산

가중치 있는 그래프 입력

int V; // 정점의 수
int E; // 간선의 수
int G[MAX_V + 1][MAX_V + 1]; // 인접행렬


scanf("%d", &V);
scanf("%d", &E);

// 인접행렬 초기화
for (int i = 0; i < V; ++i) {
    for (int j = 0; j < V; ++j) {
        G[i][j] = -1;
    }
    G[i][i] = 0;
}

// 간선을 입력 받아 인접행렬을 채운다
for (int i = 0; i < E; ++i) {
    int u, v, w;
    scanf("%d%d%d", &u, &v, &w);
    G[u][v] = w;
    G[v][u] = w;
}

DFS

깊이 우선 탐색 Depth First Search

• 길이 있는 한 계속 따라 감
• 막다른 길이면 돌아서 나오기

깊이 우선 탐색

A

B

C

E

D

F

G

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A

종료 순서: 

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B

종료 순서: 

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D

종료 순서: 

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E

종료 순서: 

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C

종료 순서: 

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C

종료 순서: C

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G

종료 순서: C

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G

종료 순서: C G

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G

종료 순서: C G E

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G F

종료 순서: C G E

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G F

종료 순서: C G E F

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G F

종료 순서: C G E F D

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G F

종료 순서: C G E F D B

깊이 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B D E C G F

종료 순서: C G E F D B A

DFS 구현 - 인접행렬

bool visited[MAX_N + 1];
bool finished[MAX_N + 1];

void DFS(int u) {
    // 이미 방문했는지 검사
    if (visited[u]) {
        return;
    }
    
    // u번째 정점을 지금 방문함
    visited[u] = true;
    printf("%d\n", u);

    // 인접한 정점을 방문
    for (int v = 1; v <= N; ++v) {
        if (v == u) continue;
        if (A[u][v]) {
            DFS(v);
        }
    }
    
    // u번째 정점 방문을 마침
    finished[u] = true;
}

격자에서 DFS하기

• 격자로 주어진 지도에서 DFS를 하는 경우
  • 임의의 좌표 (y, x) 에서 상하좌우로 이동 가능
    • (y, x) -> (y + 1, x)
    • (y, x) -> (y, x + 1)
    • (y, x) -> (y - 1, x)
    • (y, x) -> (y, x - 1)
  • 좌표 (y, x)의 정보
    • map[y][x] == 1 => 길
    • map[y][x] == 0 => 벽

격자에서 DFS하기

int Y, X;
map[MAX_ROW + 1][MAX_COL + 1];
visited[MAX_ROW + 1][MAX_COL + 1];

void dfs(int y, int x) {
    // 지도의 경계를 벗어나는지 검사
    if (y < 0 || y >= Y || x < 0 || x >= X) {
        return;
    }
    
    // 이미 방문했는지 검사
    if (visited[y][x]) {
        return;
    }

    // (y, x)를 방문
    visited[y][x] = true;
    printf("%d %d\n", y, x);

    // 인접한 칸을 방문
    dfs(y - 1, x);
    dfs(y, x - 1);
    dfs(y + 1, x);
    dfs(y, x + 1);
}

연결 요소

• 한 정점에서 간선을 따라 이동하여 방문할 수 있는 정점의 집합

연결 요소 구하기

• 한 정점에서 시작에  DFS를 이용하여 방문할 수 있는 정점은 모두 한 연결 요소에 포함된다

BFS

너비 우선 탐색 Breadth First Search

• 시작점에서 가까운 곳부터 차례대로 방문한다.

너비 우선 탐색

A

B

C

E

D

F

G

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서:

큐: A

1

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A

큐: B C

1

2

2

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B

큐: C D E

1

2

2

3

3

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C

큐: D E

1

2

2

3

3

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C D

큐: E F

1

2

2

3

3

4

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C D E

큐: F G

1

2

2

3

3

4

4

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C D E F

큐: G

1

2

2

3

3

4

4

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C D E F G

큐: 

1

2

2

3

3

4

4

너비 우선 탐색

A

B

C

E

D

F

G

방문 순서: A B C D E F G

큐: 

1

2

2

3

3

4

4

너비 우선 탐색 구현 - 인접행렬

push(int v) {
    if (visited[v] == false) {
        pushQueue(v);
        visited[v] = true;
    }
}
...

push(start);
int step = 0;
while (!queueIsEmpty()) {
    step++;
    int queue_size = queueSize();
    for (int i = 0; i < queue_size; ++i) {
        int u = pop();
        printf("%d\n", u);
        for (int v = 1; v <= N; ++v) {
            if (u != v && G[u][v]) {
                push(v);
            }
        }
    }
}

너비 우선 탐색 구현 - 격자

dy[] = { 1, 0, -1, 0 };
dx[] = { 0, 1, 0, -1 };
...

push(startPoint);
int step = 0;
while (!queueIsEmpty()) {
    step++;
    int queue_size = queueSize();
    for (int i = 0; i < queue_size; ++i) {
        Point p = pop();
        printf("%d %d\n", p.x, p.y);
        for (int d = 0; d < 4; ++d) {
            Point next;
            next.x = p.x + dx[d];
            next.y = p.y + dy[d];
            push(next);
        }
    }
}

너비 우선 탐색 구현 - 나이트

dy[] = { 2, 1, -1, -2, -2, -1, 1, 2};
dx[] = { 1, 2, 2, 1, -1, -2, -2, -1};
...

push(startPoint);
int step = 0;
while (!queueIsEmpty()) {
    step++;
    int queue_size = queueSize();
    for (int i = 0; i < queue_size; ++i) {
        Point p = pop();
        printf("%d %d\n", p.x, p.y);
        for (int d = 0; d < 8; ++d) {
            Point next;
            next.x = p.x + dx[d];
            next.y = p.y + dy[d];
            push(next);
        }
    }
}

최단거리

최단 거리

• 한 정점에서  다른 정점으로 가는 최단 거리를 구하는 문제
• 네비게이션

간선의 가중치가 모두 1인 경우

• BFS를 이용하여 구할 수 있다.
  • BFS의 depth가 시작정점에서 부터의 거리

플로이드 알고리즘

• 그래프의 모든 쌍에 대해서 최단 거리를 구하는 방법
• 가중치가 음수인 싸이클이 없어야 함
• O(V^3)

플로이드 알고리즘 구현

for (int u = 1; u <= V; ++u) {
    for (int v = 1; v <= V; ++v) {
        D[u][v] = G[u][v];
    }
}

for (int k = 1; k <= V; ++k) {
    for (int u = 1; u <= V; ++u) {
        for (int v = 1; v <= V; ++v) {
            if (D[u][v] > D[u][k] + D[k][v]) {
                D[u][v] = D[u][k] + D[k][v];
            } 
        }
    }
}

플로이드 알고리즘 활용 - 1

• 모든 쌍에 대해 최단 거리를 알고 싶을 때

플로이드 알고리즘 활용 - 2

• 모든 쌍에 대해 연결성을 확인하고 싶을 때

for (int u = 1; u <= V; ++u) {
    for (int v = 1; v <= V; ++v) {
        D[u][v] = G[u][v];
    }
    D[u][u] = false;
}

for (int k = 1; k <= V; ++k) {
    for (int u = 1; u <= V; ++u) {
        for (int v = 1; v <= V; ++v) {
            if (D[u][k] && D[k][v]) {
                D[u][v] = true;
            } 
        }
    }
}

플로이드 알고리즘 활용 - 3

• 방향성 있는 그래프에서 싸이클이 있는지 확인할 때
  • 플로이드를 수행
  • D[i][i] = true인 i가 있으면, i -> i로 가는 경로가 있다는 의미