What is a matrix?

<Insert Keanu Reeves photo here>

Matrix

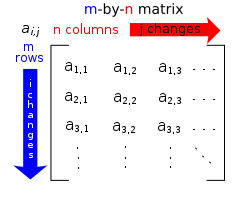
A rectangular array of values where every element belongs to a set S. A matrix has m rows and n columns. The element a_ij belongs to row ​i and column j.

More Matrices

The size of a matrix is m x n. If m = n, we say the matrix is a square matrix.

Matrix Operations

Transposition

The transpose of a matrix A, denoted by A^t, is the n x m matrix obtained by interchanging the rows and columns.

In other words, if B = A^t, then a_ij = b_ji

[1 2 t = [1 3
  3 4]     2 4]

Addition / Subtraction

Provided that two matrices are the same size, we can add or subtract matrices by adding or subtracting their elements.

[ 1 2    + [2 4  = [3 6
  3 4 ]     6 8]    9 12]

[1 2 3] + [3 4 5] = [4 6 8]

Multiplying Matrices

• For a row i in A, multiply each element by each element in a column j in B. If we have two matrices of size m x k and
  k x n
  
  AB_ij = A_i,1 * B_1,j + A_i,2 * B_2,j + A_i,3 * B_3,j + ... + A_ik + B_kj

Multiplication

Two matrices A and B can be multiplied if the number of columns in the A is the same as the number of rows in the B. Note that matrix multiplication is NOT commutative.

Given two matrices m_A x n_A and m_B x n_B, we can multiply them only if n_A = m_B. The size of the product is m_A x n_B.

Let's do a 2x2 example

[1 2  x [2 4 = [? ?
 3 4]    6 8]   ? ?]

[1 2  x [2 4 = [(1*2 + 2*6) ?
 3 4]    6 8]   ?           ?]

[1 2  x [2 4 = [14 (1*4 + 2*8)
 3 4]    6 8]   ?            ?]

Let's do a 2x2 example

[1 2  x [2 4 = [? ?
 3 4]    6 8]   ? ?]

[1 2  x [2 4 = [14           20
 3 4]    6 8]   (3*2 + 4*6)   ?]

[1 2  x [2 4 = [14 20
 3 4]    6 8]   30 (3*4 + 4*8)]

Identity Matrix

The identity matrix of order n is an n x n matrix I_n = [𝛿_ij] where 𝛿_ij = 1 if i = j and is 0 otherwise. 

[1 0 0 0
 0 1 0 0
 0 0 1 0
 0 0 0 1]

Inverse Matrix

The inverse of an n x n matrix A is the the matrix A^-1 such that AA^-1 = I (the identity matrix).

Symmetric

A matrix A is symmetric if it is equal to its transpose. That is, A = A^t. For example, the identity matrix is symmetric.

[1 0 0 0
 0 1 0 0
 0 0 1 0
 0 0 0 1]

Zero-One Matrices

Zero-One Matrix

A matrix where all the values are either 0 or 1. We can define logic-like operators on it.

The join of zero-one matrices A and B is a_ij v b_ij for each element in A and B.

The meet of zero-one matrices A and B is a_ij ^ b_ij for each element in A and B.

Boolean Product

Similar to matrix multiplication, we can find a boolean product of two matrices. Instead of multiplication, we have ^, and instead of addition we have v.

That is, if we're multiplying two matrices of size m x k and k x n:

c_ij = (a_i,1 ^ b_1,j) v (a_i,2 ^ b_2,j) v ... v (a_i,k ^ b_k,j)