Parameter Recovery and what you never dared to ask about it
Jan Göttmann, M.Sc.

Outline
- Parameter Recovery
- Why Parameter Recovery
- General Approach
- Possible Measures
- Take Home Message
- The Memory Measurement Model (M3)
- Short Recap
- Parameter Recovery
- Experimental Designs
- Empirical Results
- Drift Diffusion Model
- Short Recap
- Experimental Paradigms
- Experimental Features

Parameter Recovery: But why?
Let's gather some input from
this audience of experts !
Parameter Recovery: But why?
Parameter Recovery
- A models ability to estimate the true parameters generating the data is unknown
- Problem: probabilisitc models never recover the data perfectly!
- If the parameter recovery is not good enough the parameters are not meaningful !
We need to asses the parameter recovery to be confident about parameter driven inferences!

Parameter Recovery: But why?
Parameter Recovery
- Cognitive measurement models are designed to map the latent processes of specific experimental tasks
- Therefore, the data generated by the task will influence the parameter recovery!
- This is in particular relevant for new models ! ( e.g. M3)
But which experimental features should a task for a new measurement model have ?

Parameter Recovery: But why?
Parameter Recovery
Problem: The parameter recovery can depend on many factors
- Amount of data (e.g. Trials)
- Range of the data (e.g. outliers)
- Richness of data (e.g. differences in experimental conditions)
- Model specific requirements (e.g. specific data categories)
- Mathematical properties of the parameters
- ...

Parameter Recovery: General Approach
General Approach
How can we assess the parameter recovery ?
- Monte Carlo Methods - fitting a model many times to synthetic data under different conditions
- The data is generated by the model itself from randomly drawn parameter values !
- Therefor the ground truth of parameters is known !
Variation of recovery over the simulation factors allow to draw infereces about
experimental designs !

Parameter Recovery: General Approach
Random Sampling of Parameter values
Simulate Data from the randomly sampled parameter values under different conditions
Estimate model parameters from synthetic data
Compare the estimated parameter with the true parameters (e.g. correlation, deviation)

Parameter Recovery: Measures
How to quantify the recovery ?
- Correlation
- Pro: easy interpretation, high correlation indicates a good recovery
- Con: only relativ measure, says nothing about the absolute deviation, possible biases
Measures of parameter recovery
- Root Mean Squared Error
- Pro: gives absolute measure of deviation from true parameters
- Con: harder to interpret, depends on scale of parameters (but can be normalized), which deviation is acceptable ?

Parameter Recovery: Measures
How to quantify the recovery ?
- Residual Distributions
- Shape, Mean and Variance are rich on information about potential systemical biases
- A symmetric distribution around 0 indicates an unbiased estimation
- Skewness and Kurtosis can be used to assess biases and stability of the estimates
Measures of parameter recovery
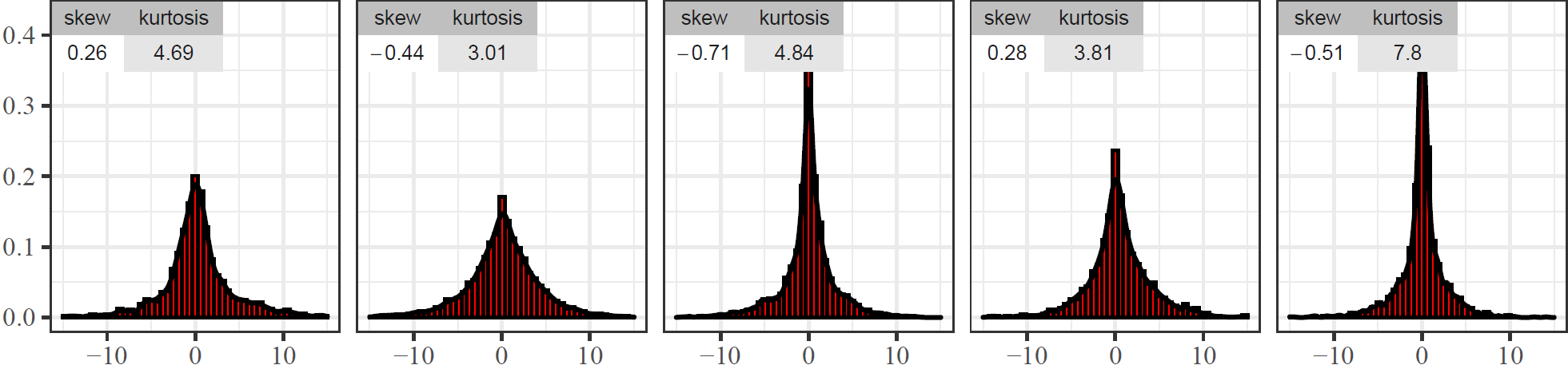

Take Home Message
-
Parameter recovery benchmarks a models ability to estimate the true parameters which generated the data
-
It is necessary to investigate the optimal data/experimental features for a precise and meaningful parameter estimation
- The general approach to estimate the parameter recovery is running Monte Carlo simulations for different influecing factors (depending on model and task)

- Correlational and deviation measures, as well as distributional properties of the residuals are well suited to asses the parameter recovery

The Memory Measurement Model (M3)

M3: Short Recap
- Simple measurement models for simple, complex and updating like working memory tasks
- Incorporates continously varying memory activation at memory recall
- Hierachical bayesian framework
- Parsimonious
- Flexible
- easily implemented in different languages (R, STAN etc.)
Very interesting for inter-individual differences research!

Benefits
M3: Short Recap
- Group Level Parameters show acceptable recovery
- Group-level parameters can map aging effects in memory decline
- No systematic parameter trade-offs
- No data for the recovery of subject-level parameters
- Which experimental features are important to achieve a good parameter recovery?

Emprical results
Current Research
M3: Short Recap
Memoranda
Memoranda
Memoranda
Read out loud
Read out loud
Read out loud
First Position has to be recalled
Time
F
V
L
C
H
M
M
H
F
L
H
O
D
T
V
C
Z
B
K
P
J
R
Other Item
Distractor in other Position
Not Presented Lure (NPL)
Correct Item
Distractor in Position

M3: Short Recap
V
F
L
M
C
H
Memoranda
Memoranda
Memoranda
Read out loud
Read out loud
Read out loud
Second Position has to be recalled
Time
C
F
M
K
B
L
P
H
Z
V
H
O
D
T
R
J
Other Item
Distractor in other Position
Not Presented Lure (NPL)
Correct Item
Distractor in Position

M3: Short Recap
F
V
L
M
C
H
Memoranda
Memoranda
Memoranda
Read out loud
Read out loud
Read out loud
First Position has to be recalled
Time
Correct Item
Distractor in Position
Distractor in other Position
Other Item
Not Presented Lure (NPL)

M3: Short Recap
Freetime t: Short vs. Long
Freetime t: Short vs. Long
Freetime t: Short vs. Long
F
V
L
M
C
H
Memoranda
Memoranda
Memoranda
Read out loud
Read out loud
Read out loud
First Position has to be recalled
Time
Correct Item
Distractor in Position
Distractor in other Position
Other Item
Not Presented Lure (NPL)
M3: Parameter Recovery
Main Goal: Figure out how to set up experimental designs to fit the M3 parameters
-
Can subject-level parameters be recovered sufficiently precise?
-
Which factors are important for the estimation of subject-level parameters?
- How many experimental trials are needed for the estimation of subject-level parameters?
Research Questions

M3: Parameter Recovery
- Sample Size: 100 simulated subjects
- N – Number of IOPs or DIOPs: 1 to 5
- K – Number of NPLs: 1, 2, 4, 8, 16
- Retrievals per subject: 100, 250, 500,1000
- nFT – Number of different Freetime Conditions (Extended Encoding Model)
- Fixed filtering parameter (Extended Encoding Model)
- 100 Repetitions per factor combination
5 x 5 x 4 x 100 = 10000 Model runs for Simple and Complex Span Models
5 x 5 x 4 x 2 x 2 x 100 = 40000 Model runs for the Extended Encoding Model
Fixed Simulation Factors
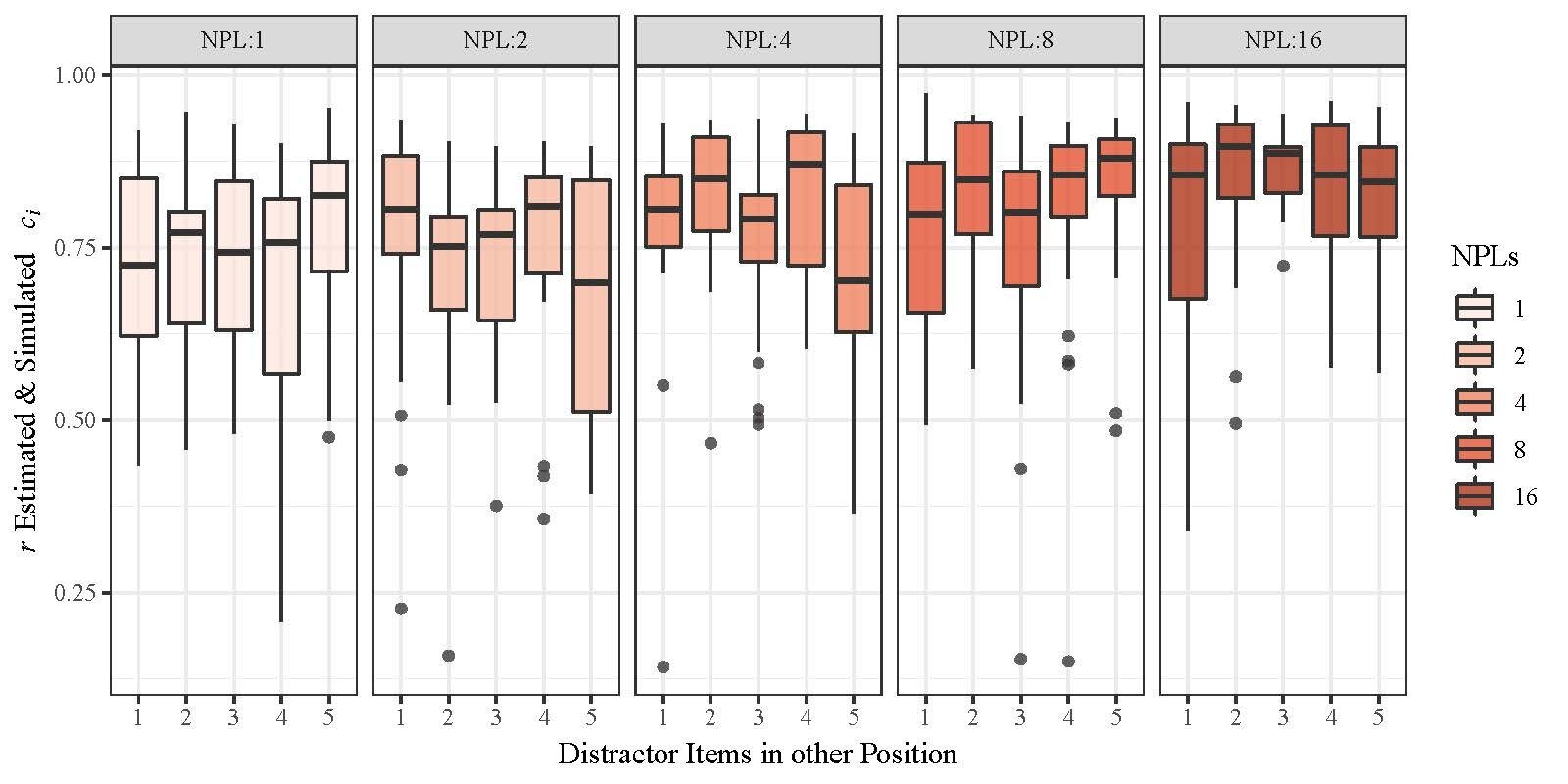
c : r = [ .72;.88]
a : r = [.68;.86]
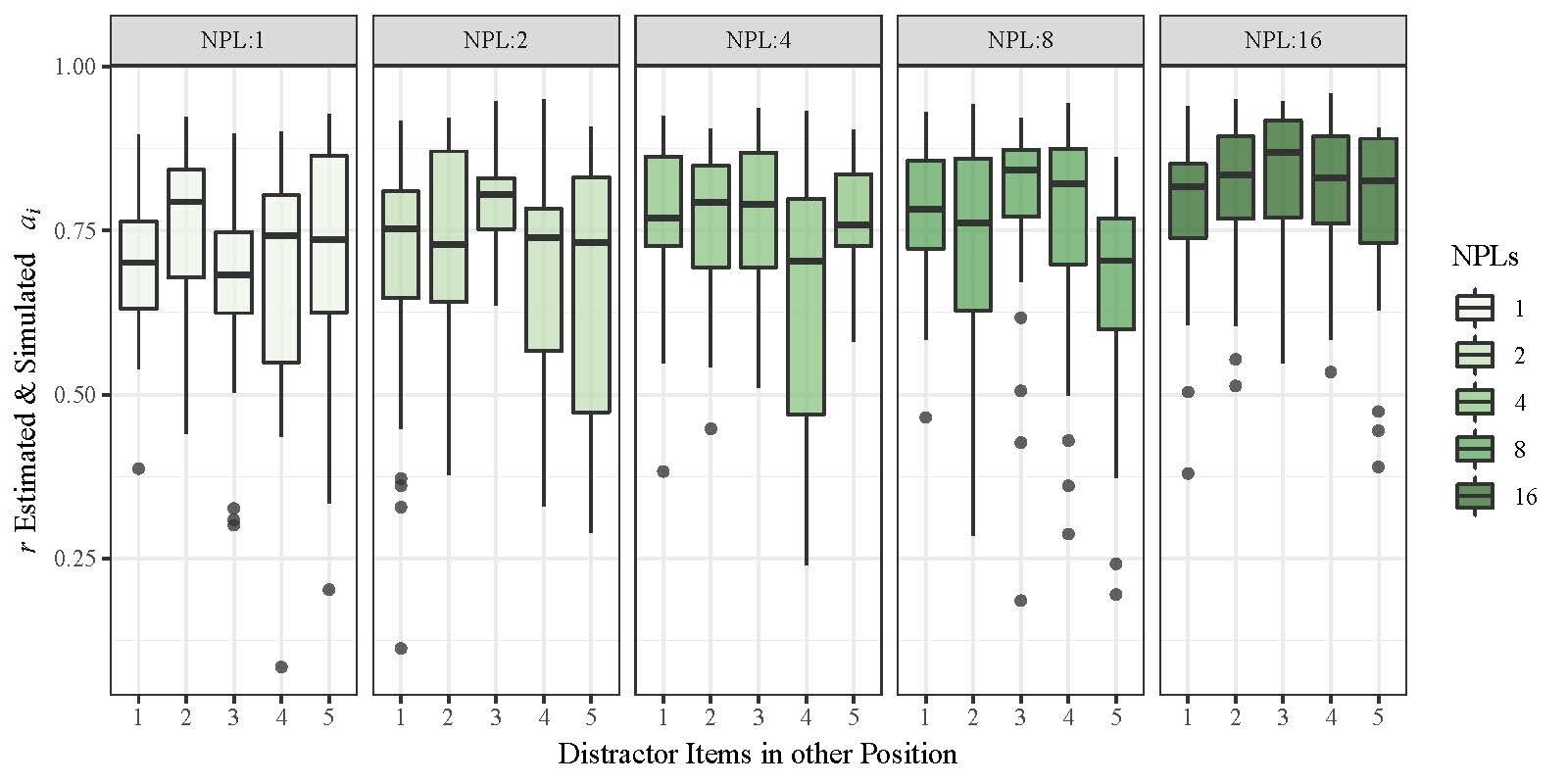
M3: Parameter Recovery
Complex Span Model

M3: Parameter Recovery
Complex Span Model
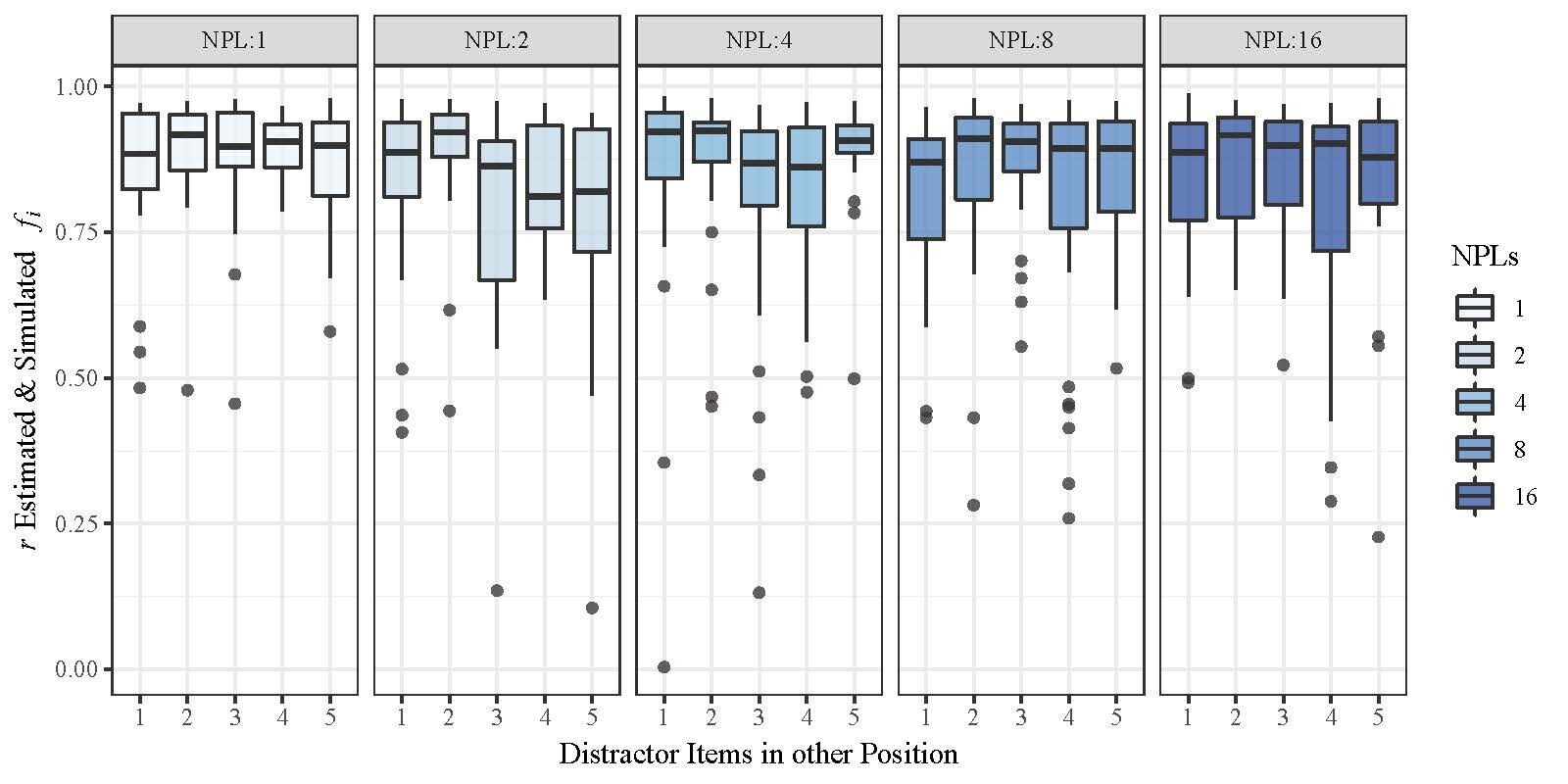
f : r = [ .83;.91]
Good overall recovery for subject-level parameters of the complex span model !

M3: Parameter Recovery
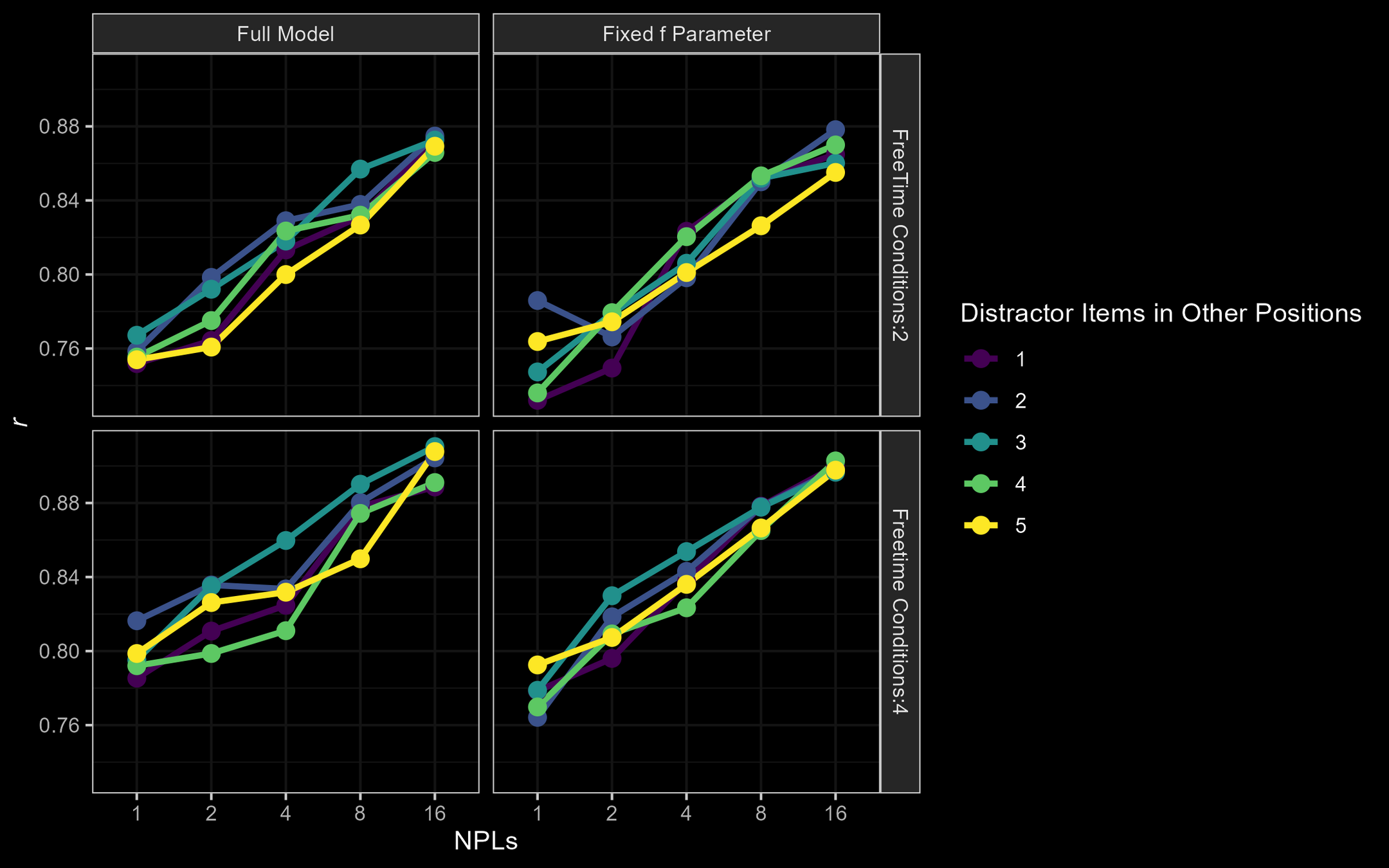
Complex Span Extended Encoding
EE full: r = [ .84;.95]
EE fixed f : r = [ .85;.95]

M3: Parameter Recovery
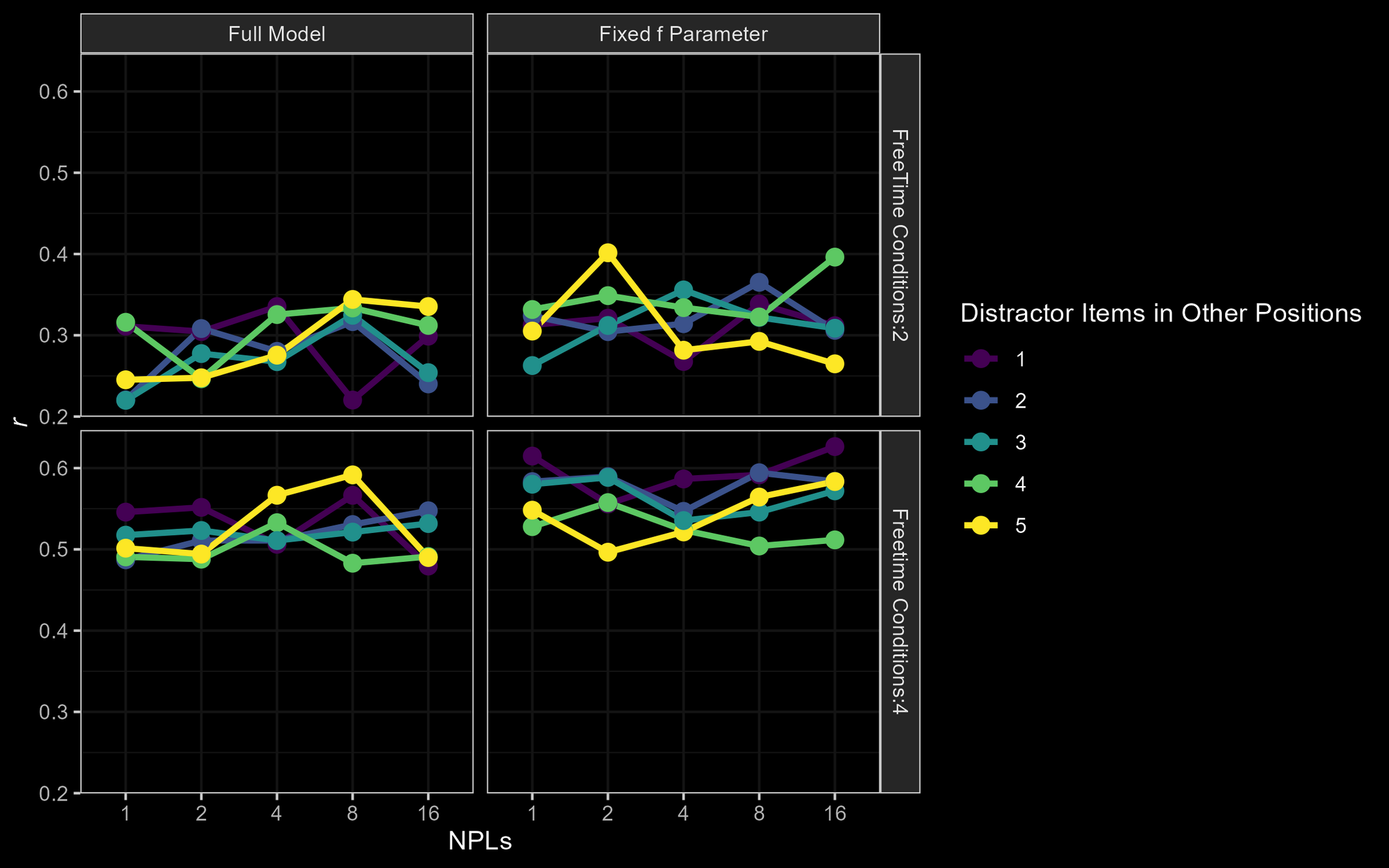
Complex Span Extended Encoding
r full: r = [ .22;.59]
r fixed f : r = [ .26;.62]

M3: Parameter Recovery
Complex Span Extended Encoding
c full : r = [ .75;.91]
c fixed f : r = [ .73;.90]


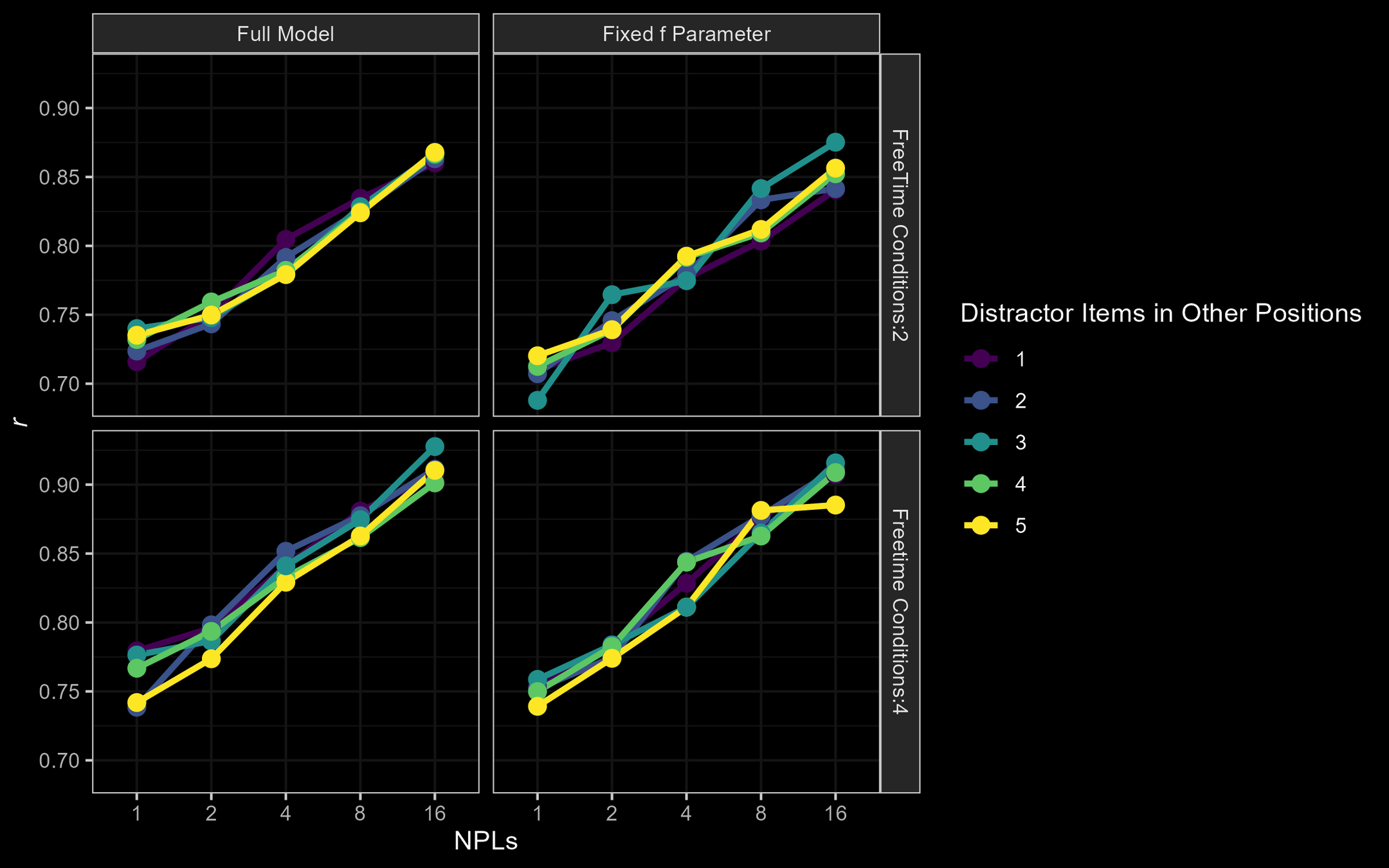
M3: Parameter Recovery
Complex Span Extended Encoding
a full: r = [ .72;.92]
a fixed f : r = [ .69;.92]

M3: Parameter Recovery
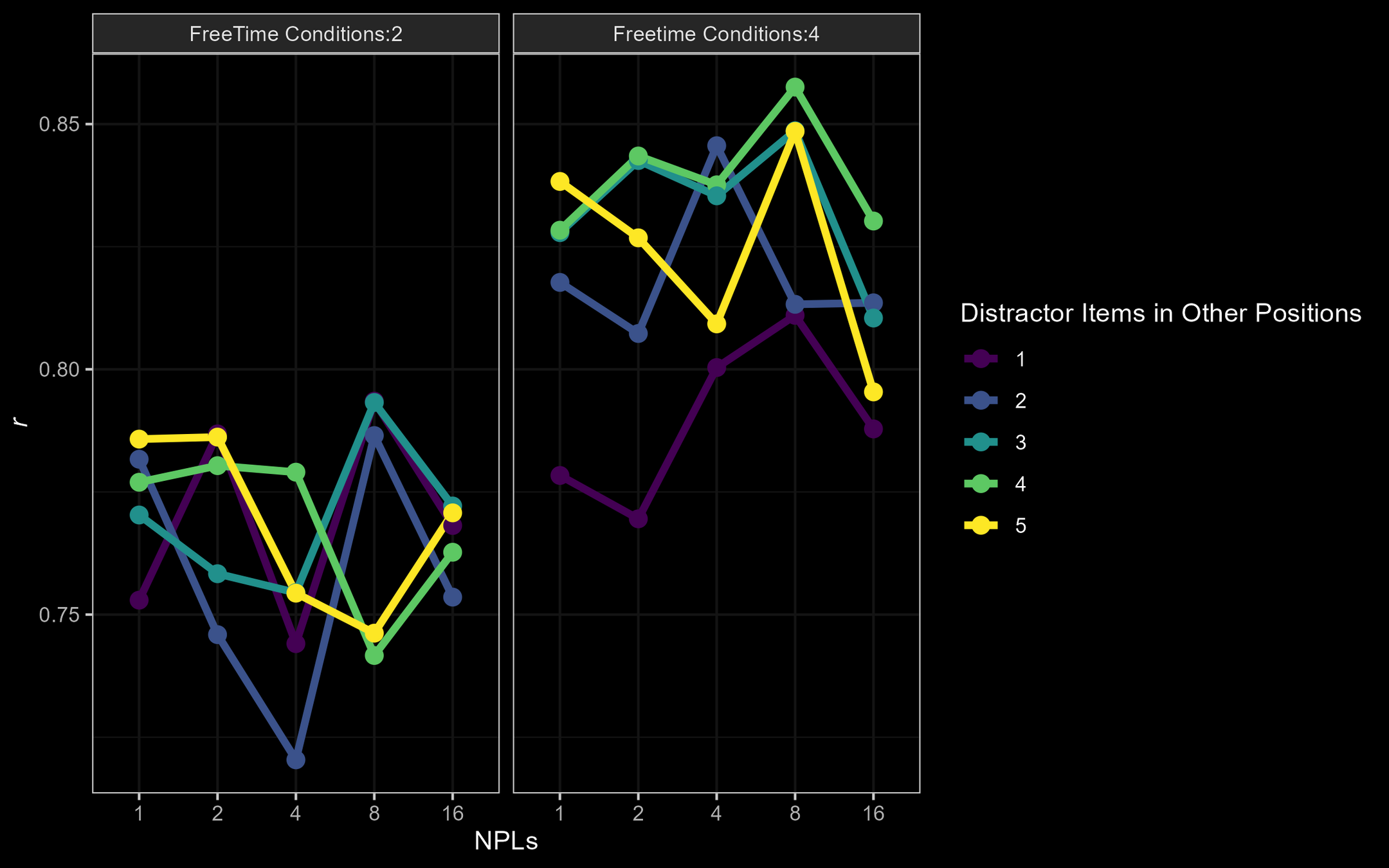
Complex Span Extended Encoding
f full: r = [ .72;.85]

M3: Experimental Designs
General Conlusions
- Subject Parameters can be recoverd with acceptable to very good fit for the complex span model !
- The removal parameter of the extended encoding model is difficult to identify
Important experimental features
- Sufficient Number of NPLs ! Minimum of 8 NPLs should scale the response set!
- At least two freetime conditions
- 250 retrievals minimum, but 500 even better (but time consuming)


M3: Experimental Designs
General Conlusions
- Subject Parameters can be recoverd with acceptable to very good fit for the complex span model !
- The removal parameter of the extended encoding model is difficult to identify
Important experimental features
- Accuracy has to midranged to maximize the precision - avoid floor and ceiling effects!


M3: Empirical Application
Relationship of M3 Parameters and Intelligence
- N = 38
- Hagener Matrices Test (HMT) for intelligence Assessment
- Fittet M3 Complex Span Model (subject level)
- WMC (Symmetry Span), Flanker Task for further analysis
- Visual Cued Complex Span Task

M3: Empirical Application
?
Choose brighter
color
Choose brighter
color
Choose brighter
color
Horizontal Dimension relevant
Vertical Dimension relevant
Vertical Dimension relevant
M3: Empirical Application
?

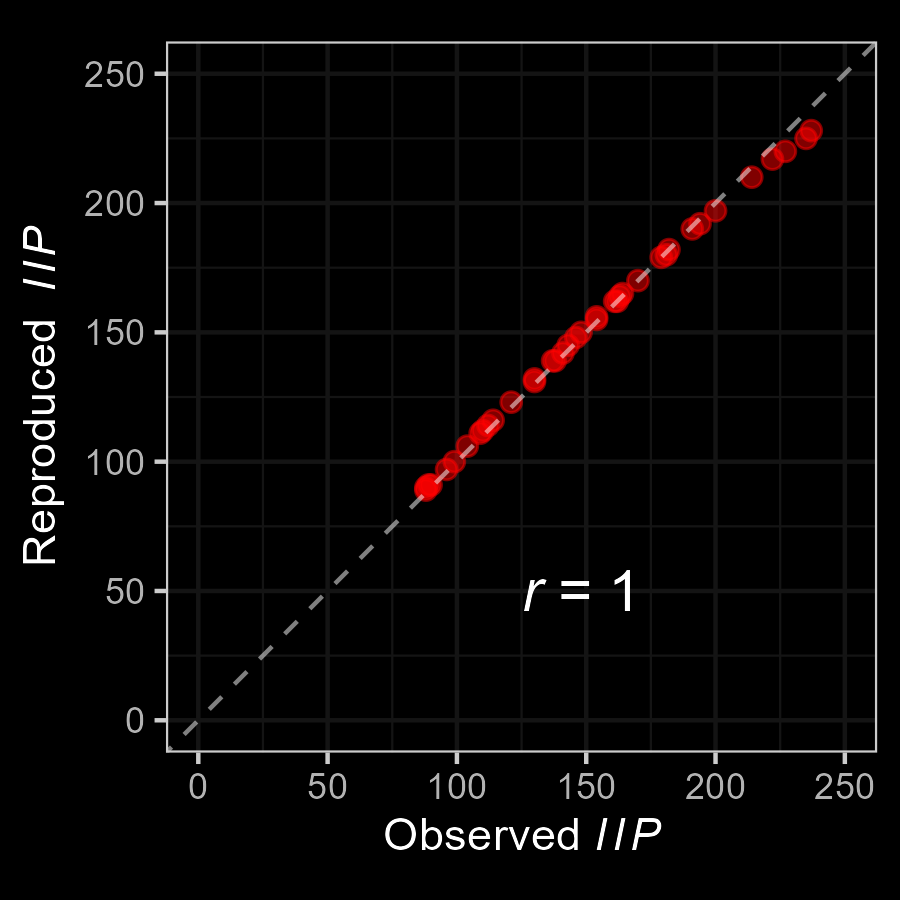
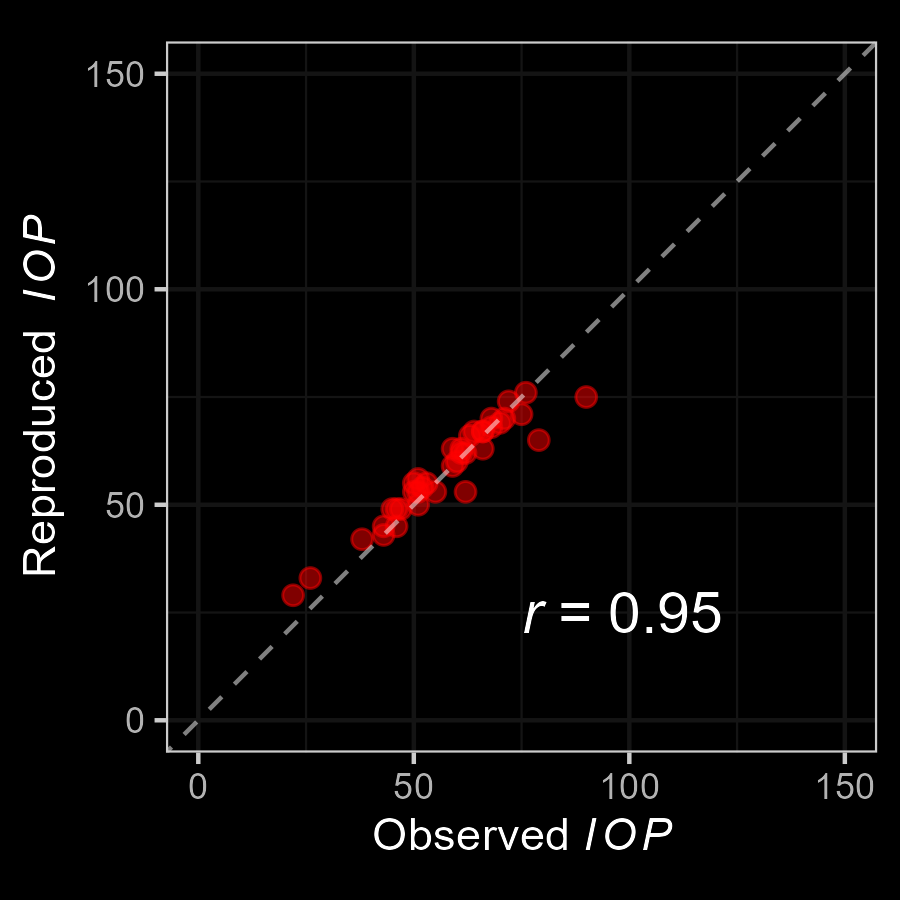
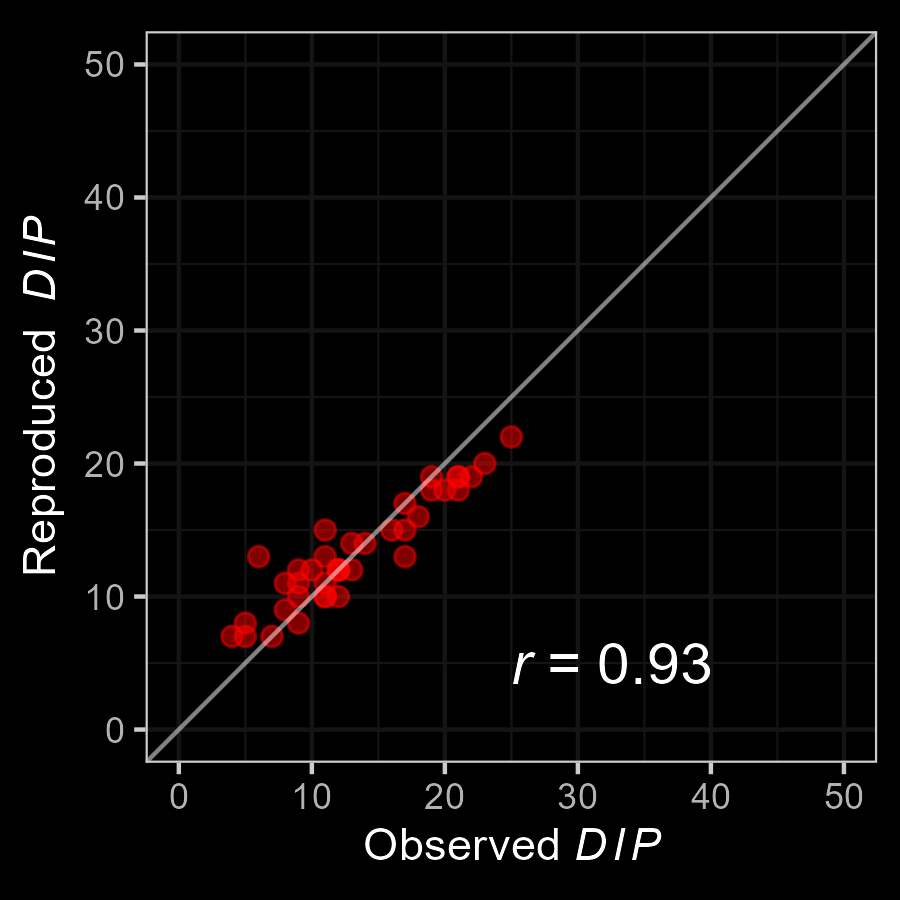
M3: Empirical Application

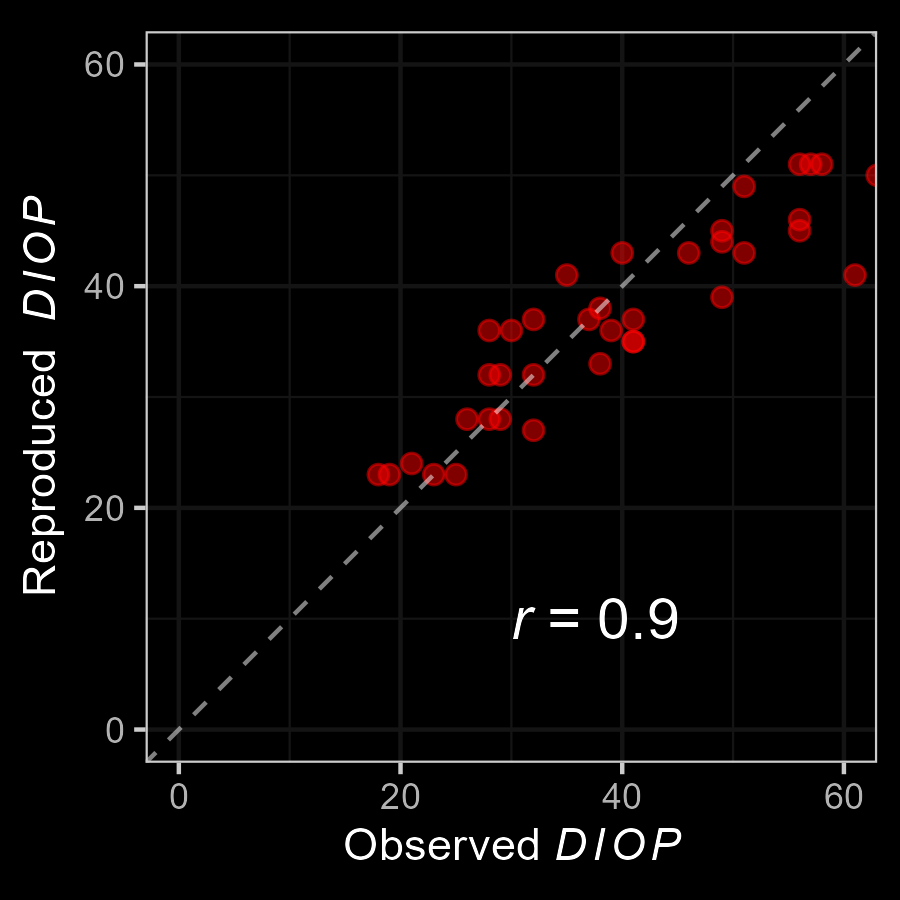
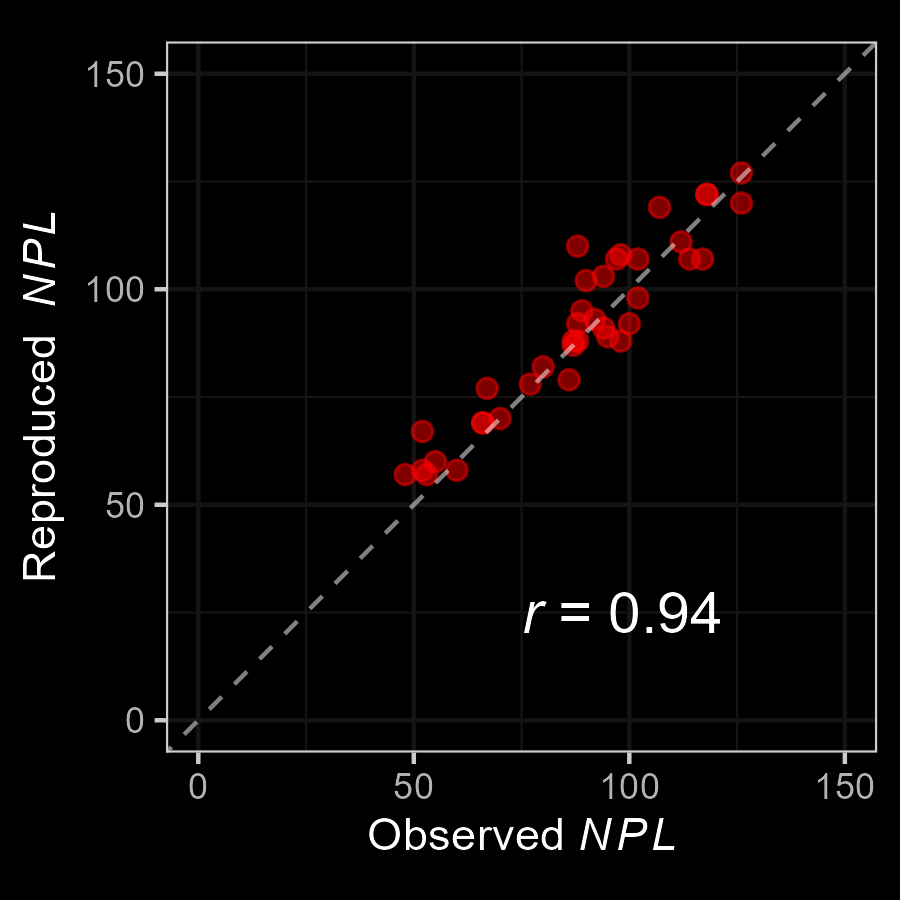
Very good fit to the data!
M3: Empirical Application

M3: Empirical Application
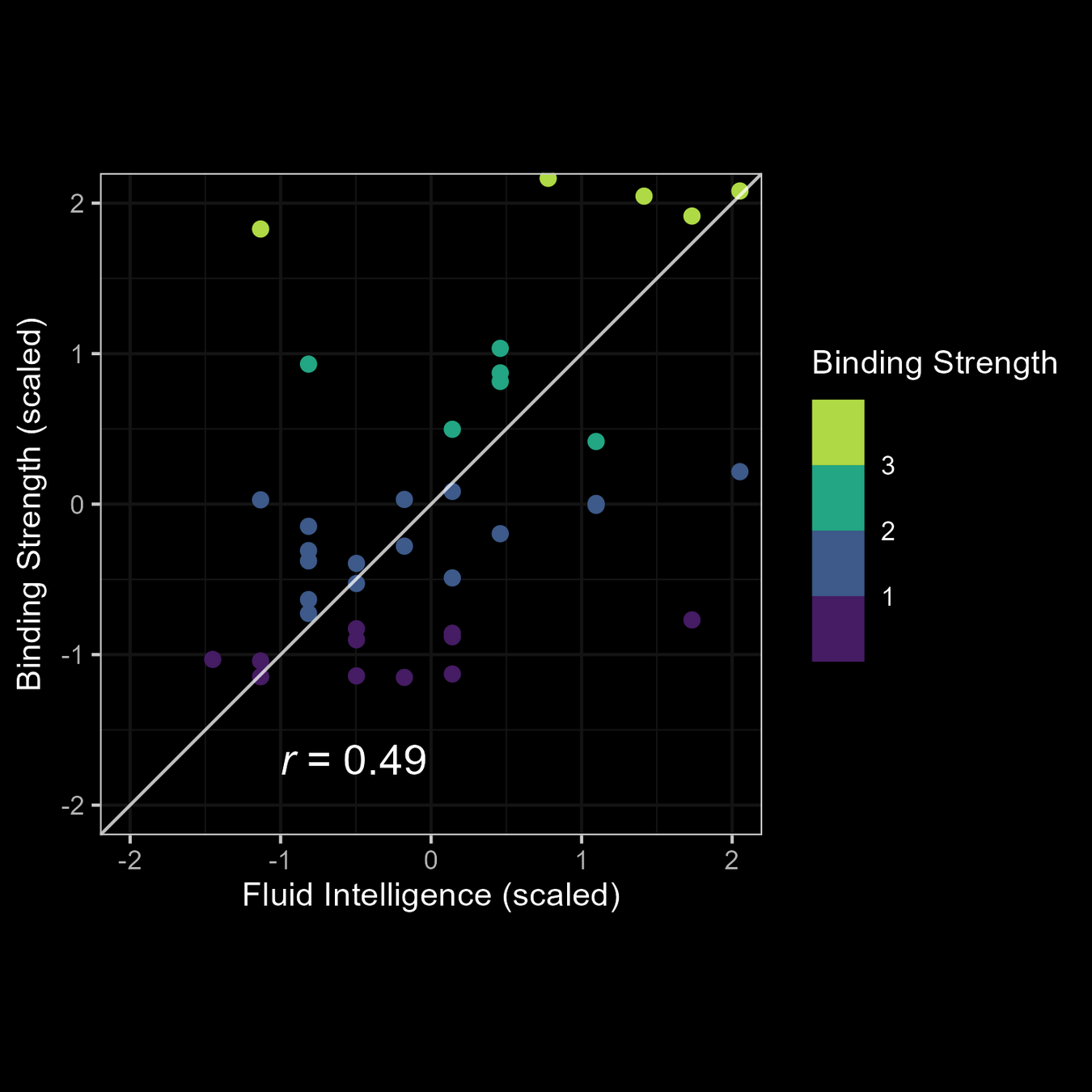
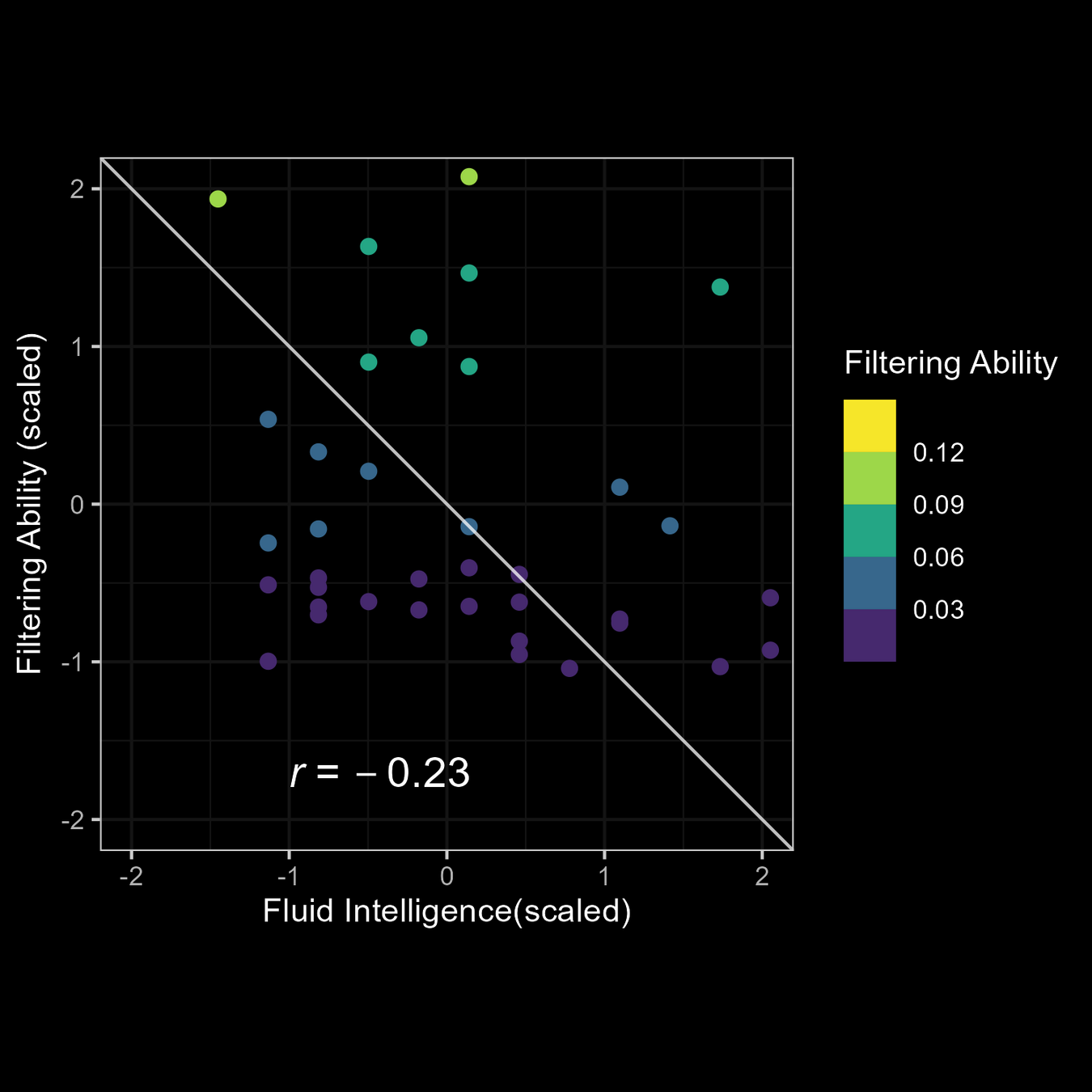
Relationship of M3 Parameters with fluid intelligence
The Drift Diffusion Model
(DDM)

DDM: Short Recap
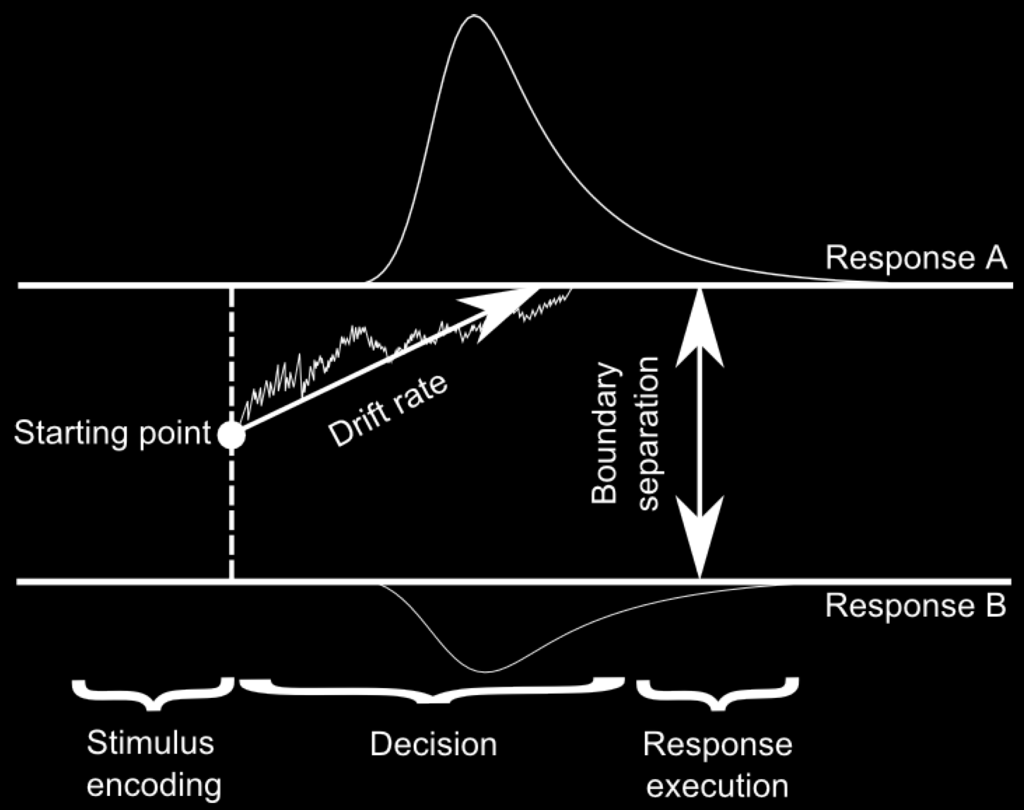
Parameters
v - drift rate
t0 - non-decision time
a - boundary seperation
z - starting point

DDM: Experimental Paradigms
Experimental Prerequisits
- Binary Choice Tasks
- Two thresholds represent two alternatives decisions
- Conflicting binary Stimuli
- Possibly also multiple choice tasks
- Recoding in correct (upper threshold) and incorrect (lower threshold)
- Alternative: Linear Ballistic Accumulator Model

DDM: Experimental Paradigms
Experimental Tasks


Judgement of color, brightness or frequencies (Voss, Rothermund & Voss, 2004; Rothermund & Brandtstädter, 2008)
- no a priori bias
- can be coupled with valence
- high eyeball validity for sequential sampling

DDM: Experimental Paradigms
Experimental Tasks
Lexical Decision Tasks
(e.g. Ratcliff, Gomez & McKoon, 2004)
-
Type of word can be distinguished by drift rate:
v(non-word) < v(pseudo-word) < 0 < v(rare word) < v(frequent word)
v(„Cxsdsw“) < v(„Silden“) < 0 < v(„Moschee“) < v(„Haus“) - But: no clear eyeball validity for sequential sampling

DDM: Experimental Features
Experimental Features
- Fast Reactions (but not to fast)
- usually between 300 ms and 1500 ms
- fast outliers lead to estimation biases
- long reaction times should be avoided
- for longer RTs s it is unclear, wether the drift rate and the threshold separation are stable within a trial
But: Validity for the parameters are also given for longer RTs of ~ 10 seconds (Lerche & Voss, 2019)

DDM: Experimental Features
Experimental Features
- Number of experimental trials per condition
- Typical data (e.g. Ratcliff & Rouder, 1998)
3 Subjects x 10 Sessions x 8 Blocks x 102 Trials (~ 8000 Trials) - But: amount of needed trials depends on discrepancy function
- 50 trials as rule of thumb (fitted with Kolmogorov-Smirnoff (KS) criterion
- For a low number of trials, maximum likelihood estimation is recommended
- Typical data (e.g. Ratcliff & Rouder, 1998)

DDM: Take Home Messages
- The DDM is suited for binary choice tasks - multiple choice tasks have to be recoded
- possible tasks are Lexical Decision Tasks, or Feature Judgement Tasks
- Reaction Times should be in a range between 300 and 1500 ms - although validity is also given for longer RTs!
- 50 Trials (per condition) as rule of thumb to estimate the parameters
- For low amount of trials Maximum Likelihood estimation is recommended (for fast-dm)


Thank you for Your Attention!

@JanGoettmann
github.com/jgman86

jan.goettmann@uni-mainz.de
