Design

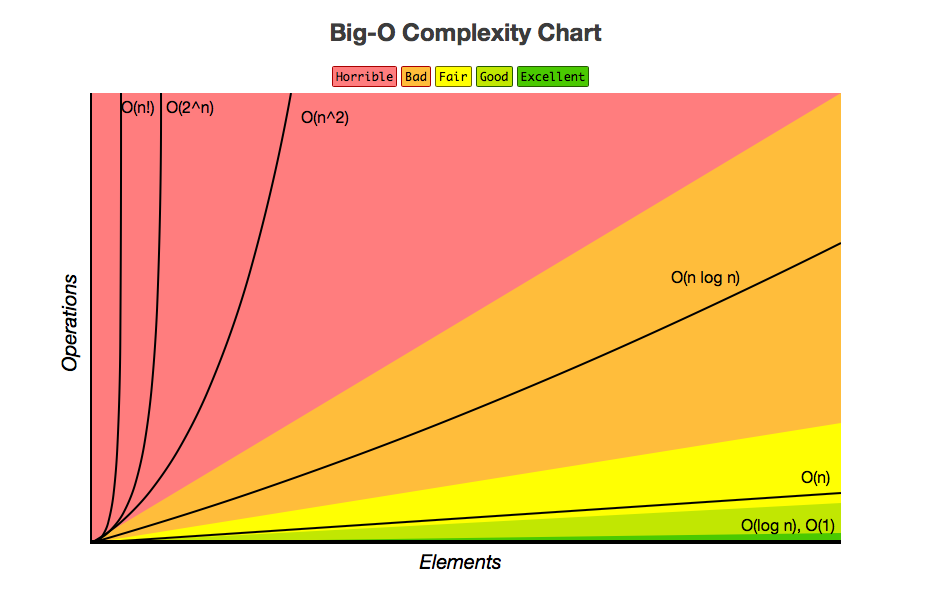
Big O

Design a stock api

class System { // assume time being used is unique
public:
    int getMax() {} //O(1)
    
    int getMin() {} //O(1)
    
    int getRecent() {} //O(1)
    
    void add(long time, int price) {}
    
    void update(long time, int price) {}
    
    void remove(long time) {}
    
private:

};

Design a stock api

int getMax() {} //O(1) ?
Data structure?

Design a stock api

int getMax() {} //O(1) ?
Data structure?

Array,

Linked list,
Tree,

Queue,

Stack,

Graph

HashMap

Heap

Design a stock api

int getMax() {} //O(1) ?
Data structure?

sorted Array,

sorted Linked list,
binary Tree,

Queue,

Stack,

Graph

HashMap

Heap

Design a stock api

int getMin() {} //O(1) ?
Data structure?

sorted Array,

sorted Linked list,
binary Tree,

Queue,

Stack,

Graph

HashMap

Heap

Design a stock api

int getRecent() {} //O(1) ?
Data structure?

sorted Array,

sorted Linked list,
binary Tree,

Queue,

Stack,

Graph

HashMap

Heap

Design a stock api

void add(long time, int price) {}

void update(long time, int price) {}

void remove(long time) {}

TimeStamp

Price

Design a stock api

void add(long time, int price) {}

void update(long time, int price) {}

void remove(long time) {}

TimeStamp

Price

ordered!(sorted)

Design a stock api

TimeStamp and Price ordered!(sorted)

two way:

1, sorted algorithm

2, sorted structure

sort algorithm

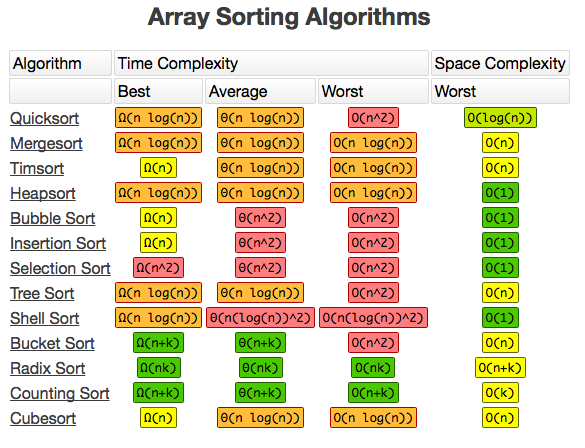
sort structure

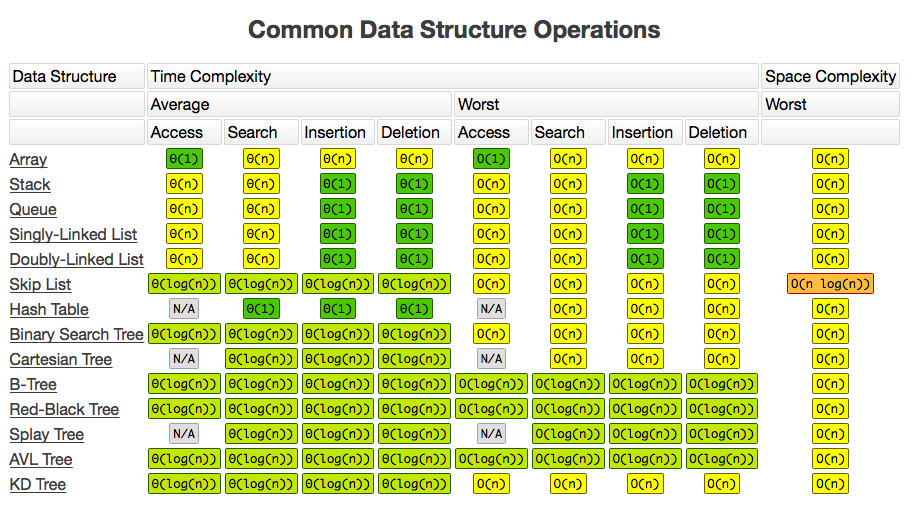
Design a stock api

TimeStamp and Price ordered!(sorted)

two way:

1, sorted algorithm (n log n for every operation)

2, sorted structure (log n for every operation)

Design a stock api

TimeStamp and Price ordered!(sorted)

two way:

1, sorted algorithm (n log n for every operation)

2, sorted structure (log n for every operation)

heap, Set

Design a stock api

Component:

1, hash map O(1) time

2, sorted structure Set O(log n) time

How to combine them?

Design a stock api

Component:

1, hash map O(1) time

2, sorted structure Set O(log n) time

How to combine them?

iterator, pair

class System {
private:
	unordered_map<long,pair<set<pair<int,long>::iterator,set<pair<long,int>::iterator> 
            map_;
	set<pair<int,long>> prices;
	set<pair<long,int>> times;
};

Key

class System {
private:
	unordered_map<long,pair<set<pair<int,long>::iterator,set<pair<long,int>::iterator> 
            map_;
	set<pair<int,long>> prices;
	set<pair<long,int>> times;
public:
	void add(long time, int price) {
		auto it1 = prices.insert(make_pair(price, time)).first;
		auto it2 = times.insert(make_pair( time,price)).first;
		map_[time] = make_pair(it1,it2);
	}
	void update(long time, int price){
		prices.erase(map_[time].first);
		times.erase(map_[time].second)
		add(time, price);
	}
	void remove(long time){
		prices.erase(map_[time].first);
		times.erase(map_[time].second)
		map_.erase(time);
	}

	int getMostRecent(){
		return times.rbegin()->second;
	}
	int getMinPrice(){
		return prices.begin()->first;
	}
	int getMaxPrice(){
		return prices.rbegin()->first;
	}
};

class System { // assume time being used is unique
public:
    int getMax() {
        return priceIndex_.rbegin()->first;
    }
    int getMin() {
        return priceIndex_.begin()->first;
    }
    int getRecent() {
        return timeIndex_.rbegin()->second->second;
    }
    void add(long time, int price) {
        // assume the time being added here is a distinct value
        const auto& it = list_.emplace(list_.end(), time, price);
        timeIndex_[time] = it;
        priceIndex_[price] += 1;
    }
    void update(long time, int price) {
        // assume the time being updated here exists
        auto& it = timeIndex_[time];
        auto& oldPrice = it->second;
        if (--priceIndex_[oldPrice] == 0) {
            priceIndex_.erase(oldPrice);
        }
        oldPrice = price;
        priceIndex_[oldPrice] += 1;
    }

    void remove(long time) {
        // assume the time being updated here exists
        auto& it = timeIndex_[time];
        int price = it->second;
        list_.erase(it);
        timeIndex_.erase(time);
        if (--priceIndex_[price] == 0) {
            priceIndex_.erase(price);
        }
    }
private:
    list<pair<long, int>> list_;
    map<long, list<pair<long, int>>::iterator> timeIndex_;
    map<int, int> priceIndex_;
};

Design an array api

Get, Set, SetAll // All operation is O(1)

Get(4) -> get element at index 4
Set(index, value);
SetAll(5) -> set all element to 5

class Array{
private:
public:
    Status Get(int index){}
    void Set(int index, int val){}
    void SetAll(int val){}
};

Design an array api

Get, Set, SetAll // All operation is O(1)

Get(4) -> get element at index 4
Set(index, value);
SetAll(5) -> set all element to 5

class Array{
private:
public:
    Status Get(int index){}
    void Set(int index, int val){}
    void SetAll(int val){}
};

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

Design an array api

Get, Set, SetAll // All operation is O(1)

Get(4) -> get element at index 4
Set(index, value);
SetAll(5) -> set all element to 5

class Array{
private:
public:
    Status Get(int index){}
    void Set(int index, int val){}
    void SetAll(int val){}
};

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

What's the key?

Design an array api

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

What's the key?

similar to stock?

Order?

Design an array api

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

What's the key?

O(1) operation time?

structure?

algorithm?

Design an array api

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

What's the key?

X O(1) operation time?

X structure?

X algorithm?

Add dimension

Design an array api

Get? traversal all element?

Set?traversal all element?

SetAll?traversal all element?

What's the key?

Add dimension

TIMESTAMP

Design an array api

update TIMESTAMP

during every operation

O(1)

Design an array api

update TIMESTAMP

during every operation

O(1)

Get based on timestamp

Set based on timestamp

SetAll base on timestamp

Design an array api

Get based on timestamp

Set based on timestamp

SetAll base on timestamp

Node{

int value;

int version; // timestamp

}

Get, Set, SetAll // All operation is O(1)

class Status

class node{
	int value;
	int version;
}

class Array{
private:
	int size;
	vector<node> nums;
	node setAll;
	int timestamp
public:
	Array(int sz): size(sz), timestamp(0) {
		nums.resize(sz);
        }

        Status Get(int index){
            if (nums[index].version > setAll.version) return nums[index].value;
            else return setAll.value;
        }
        void Set(int index, int val){
        	nums[index].value = val;
        	nums[index].version = timestamp++;
        }
        void SetAll(int val){
        	setAll.value = val;
        	setAll.version = timestamp++;
        }
};

LRU cache

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.

put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

Could you do both operations in O(1) time complexity?

LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

Key

data structure:

Hashtable(O(1)) + Double linked list (O(1))

class DLinkedNode {
	int key;
	int value;
	DLinkedNode pre;
	DLinkedNode post;
}

/**
 * Always add the new node right after head;
 */
private void addNode(DLinkedNode node){
	node.pre = head;
	node.post = head.post;
	
	head.post.pre = node;
	head.post = node;
}

/**
 * Remove an existing node from the linked list.
 */
private void removeNode(DLinkedNode node){
	DLinkedNode pre = node.pre;
	DLinkedNode post = node.post;
	
	pre.post = post;
	post.pre = pre;
}

/**
 * Move certain node in between to the head.
 */
private void moveToHead(DLinkedNode node){
	this.removeNode(node);
	this.addNode(node);
}

// pop the current tail. 
private DLinkedNode popTail(){
	DLinkedNode res = tail.pre;
	this.removeNode(res);
	return res;
}

Double Linked List

private Hashtable<Integer, DLinkedNode> 
	cache = new Hashtable<Integer, DLinkedNode>();
private int count;
private int capacity;
private DLinkedNode head, tail;

public LRUCache(int capacity) {
	this.count = 0;
	this.capacity = capacity;

	head = new DLinkedNode();
	head.pre = null;
	
	tail = new DLinkedNode();
	tail.post = null;
	
	head.post = tail;
	tail.pre = head;
}

public int get(int key) {
    
	DLinkedNode node = cache.get(key);
	if(node == null){
		return -1; // should raise exception here.
	}
	
	// move the accessed node to the head;
	this.moveToHead(node);
	
	return node.value;
}

public void set(int key, int value) {
	DLinkedNode node = cache.get(key);
	
	if(node == null){
		
		DLinkedNode newNode = new DLinkedNode();
		newNode.key = key;
		newNode.value = value;
		
		this.cache.put(key, newNode);
		this.addNode(newNode);
		
		++count;
		
		if(count > capacity){
			// pop the tail
			DLinkedNode tail = this.popTail();
			this.cache.remove(tail.key);
			--count;
		}
	}else{
		// update the value.
		node.value = value;
		this.moveToHead(node);
	}
	
}

class LRUCache{
private:
    int _capacity;
    list<pair<int,int>> items;
    unordered_map<int,list<pair<int,int>>::iterator> cache;
    
public:
    LRUCache(int capacity):_capacity(capacity) {}
    
    int get(int key) {
        auto it = cache.find(key);
        if(it==cache.end()) return -1;
        else{
            items.splice(items.begin(), items, cache[key]);
            return cache[key]->second;
        }
    }
    
    void set(int key, int value) {
        auto it = cache.find(key);
        if(it!=cache.end()){
            cache[key]->second = value;
            items.splice(items.begin(), items, cache[key]);
        }
        else{
            if((int)cache.size()==_capacity){
                cache.erase(items.back().first);
                items.pop_back();
            }
            items.push_front(make_pair(key,value));
            cache[key] = items.begin();
        }
    }
};

C++

http://www.zhitongguigu.com/

Homework

1,LRU Cache

2,LFU Cache

3,The Skyline Problem

4,Longest Substring Without Repeating Characters

5,Longest Substring with At Most Two Distinct Characters

6,Longest Substring with At Most K Distinct Characters

7,Longest Substring with At Least K Repeating Characters

http://www.zhitongguigu.com/

Homework

8,Container With Most Water

9,Trapping Rain Water

10, Trapping Rain Water II