Time Complexity

http://www.zhitongguigu.com/

What is Time Complexity?

Find a Number from a Array
- If the Array has 10 numbers?
- If the Array has 100 numbers?
- If the Array has 1,000,000 numbers?
We consider the input n is closing to ∞

http://www.zhitongguigu.com/

Calculate Prime

Given a number n. Is n a prime?

http://www.zhitongguigu.com/

A Prime Number can be divided evenly only by 1, or itself.
And it must be a whole number greater than 1.

Input? Output?

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Calculate Prime

Given a number n. Is n a prime?

http://www.zhitongguigu.com/

public boolean isPrime(int n) {
    // implement you method here
}

Calculate Prime

Naive Idea

http://www.zhitongguigu.com/

public boolean isPrime(int n) {
    // Sudo code
    int i from 2 -> n-1;
        if n mod i == 0
        return false
    return true
}

How many calculations?

n - 2

Calculate Prime

Better Idea

http://www.zhitongguigu.com/

public boolean isPrime(int n) {
    // Sudo code
    int i from 2 -> n / 2;
        if n mod i == 0
        return false
    return true
}

How many calculations?

n / 2 - 2

Calculate Prime

Even Better

http://www.zhitongguigu.com/

public boolean isPrime(int n) {
    // Sudo code
    int i from 2 -> Math.sqrt(n);
        if n mod i == 0
        return false
    return true
}

How many calculations?

sqrt(n) - 1

Calculate Prime

Why Square Root Works

http://www.zhitongguigu.com/

If n = a * b, then n is not a prime

If we cannot find such a (b), then n is a prime

If Math.sqrt(n) = m = 3.316, then a <= m <= b

Do we really care about b?

Conclusion: check from 2 to Math.sqrt(n)

Calculate Prime

http://www.zhitongguigu.com/

Suppose 1 calculation is 1ms

input n	(n-2)	sqrt(n) - 1:
10	8ms	2ms
10^10	10^10ms = 115 days	10^5ms = 1.66mins

Calculate Prime

Homework:

Implement the above 2

http://www.zhitongguigu.com/

Time Complexity

\Theta

\Theta

\Omega

\Omega

O

http://www.zhitongguigu.com/

Big O notation

Time Complexity

f(n) = n^2 + 2n + 5

f(n) = n^2 + 2n + 5

f(n) \in O(n^3)

f(n) \in O(n^3)

http://www.zhitongguigu.com/

If both and are right, we need to give

f(n) \in O(n^2)

f(n) \in O(n^2)

O(n^3)

O(n^3)

O(n^2)

O(n^2)

Different Time Complexity

Best Case
Worst Case
Average Case

http://www.zhitongguigu.com/

Best Example: Quick Sort

avg: O(n log n)

avg: O(n log n)

worst: O(n^2)

worst: O(n^2)

Different Time Complexity

http://www.zhitongguigu.com/

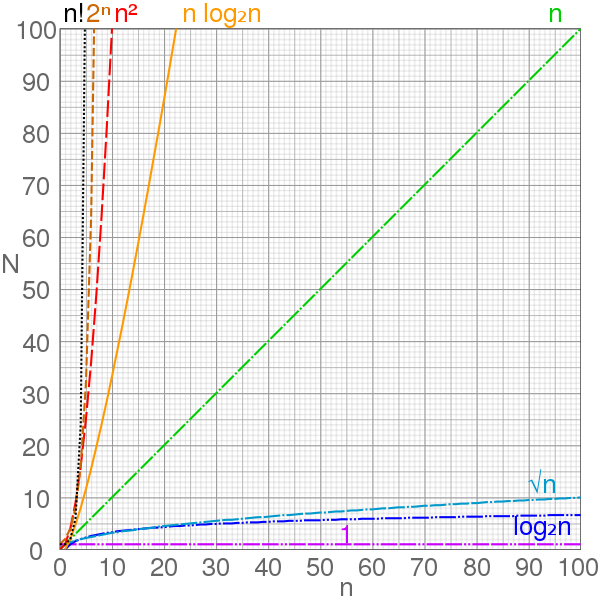
Recurrence Equation

Merge Sort: T(n) = 2T(n/2) + cn
Binary Search: T(n) = T(n/2) + c
Selection Sort: T(n) = T(n-1) + cn
Factorial: T(n) = T(n-1) + c

http://www.zhitongguigu.com/

Recursive deduction

T(n) = T(n-1) + cn

T(n-1) = T(n-2) + c(n-1)

...

T(1) = T(0) + c

T(0) = 0

http://www.zhitongguigu.com/

Recursive deduction

T(n) = T(n-1) + cn

T(n-1) = T(n-2) + c(n-1)

...

T(1) = T(0) + c

T(0) = 0

T(n) = c(0+1+2+...+n) = O(n^2)

T(n) = c(0+1+2+...+n) = O(n^2)

http://www.zhitongguigu.com/

Master Method

T(n) = aT(\frac{n}{b})+n^c

T(n) = aT(\frac{n}{b})+n^c

\text{Compare } log_ba \text{ and } c

\text{Compare } log_ba \text{ and } c

http://www.zhitongguigu.com/

https://en.wikipedia.org/wiki/Master_theorem

Master Method

T(n) = aT(\frac{n}{b})+n^c

T(n) = aT(\frac{n}{b})+n^c

\begin{cases} & \text{ if } log_ba > c, T(n) = n^{log_ba} \\ & \text{ if } log_ba = c, T(n) = n^clogn \\ & \text{ if } log_ba < c, T(n) = n^c \end{cases}

\begin{cases} & \text{ if } log_ba > c, T(n) = n^{log_ba} \\ & \text{ if } log_ba = c, T(n) = n^clogn \\ & \text{ if } log_ba < c, T(n) = n^c \end{cases}

http://www.zhitongguigu.com/

Master Method

T(n) = aT(\frac{n}{b})+n^c

T(n) = aT(\frac{n}{b})+n^c

\begin{cases} & \text{ if } log_ba > c, T(n) = n^{log_ba} \\ & \text{ if } log_ba = c, T(n) = n^clogn \\ & \text{ if } log_ba < c, T(n) = n^c \end{cases}

\begin{cases} & \text{ if } log_ba > c, T(n) = n^{log_ba} \\ & \text{ if } log_ba = c, T(n) = n^clogn \\ & \text{ if } log_ba < c, T(n) = n^c \end{cases}

http://www.zhitongguigu.com/

Example: Binary Search T(n) = T(n/2) + m

a = 1, b = 2, c = 0

It fits the second condition. So T(n) = logn

Recurrence Equation

Merge Sort: T(n) = 2T(n/2) + cn
Binary Search: T(n) = T(n/2) + c
Selection Sort: T(n) = T(n-1) + cn
Factorial: T(n) = T(n-1) + c

http://www.zhitongguigu.com/

O(n log n)

O(n log n)

O(log n)

O(log n)

O(n^2)

O(n^2)

O(n)

O(n)

How to get the recursive equation

How do you solve the problem?
How do you divide the problem into smaller part?
Before going into smaller parts, how many operation do you need?

http://www.zhitongguigu.com/

Homework

Count Primes

http://www.zhitongguigu.com/

Count the number of prime numbers less than a non-negative number, n.