Algoritmo
de
LOUVAIN
Germán Grandas
Jhoan Marín
Detección
de
Comunidades

Algoritmos
De
Modularidad
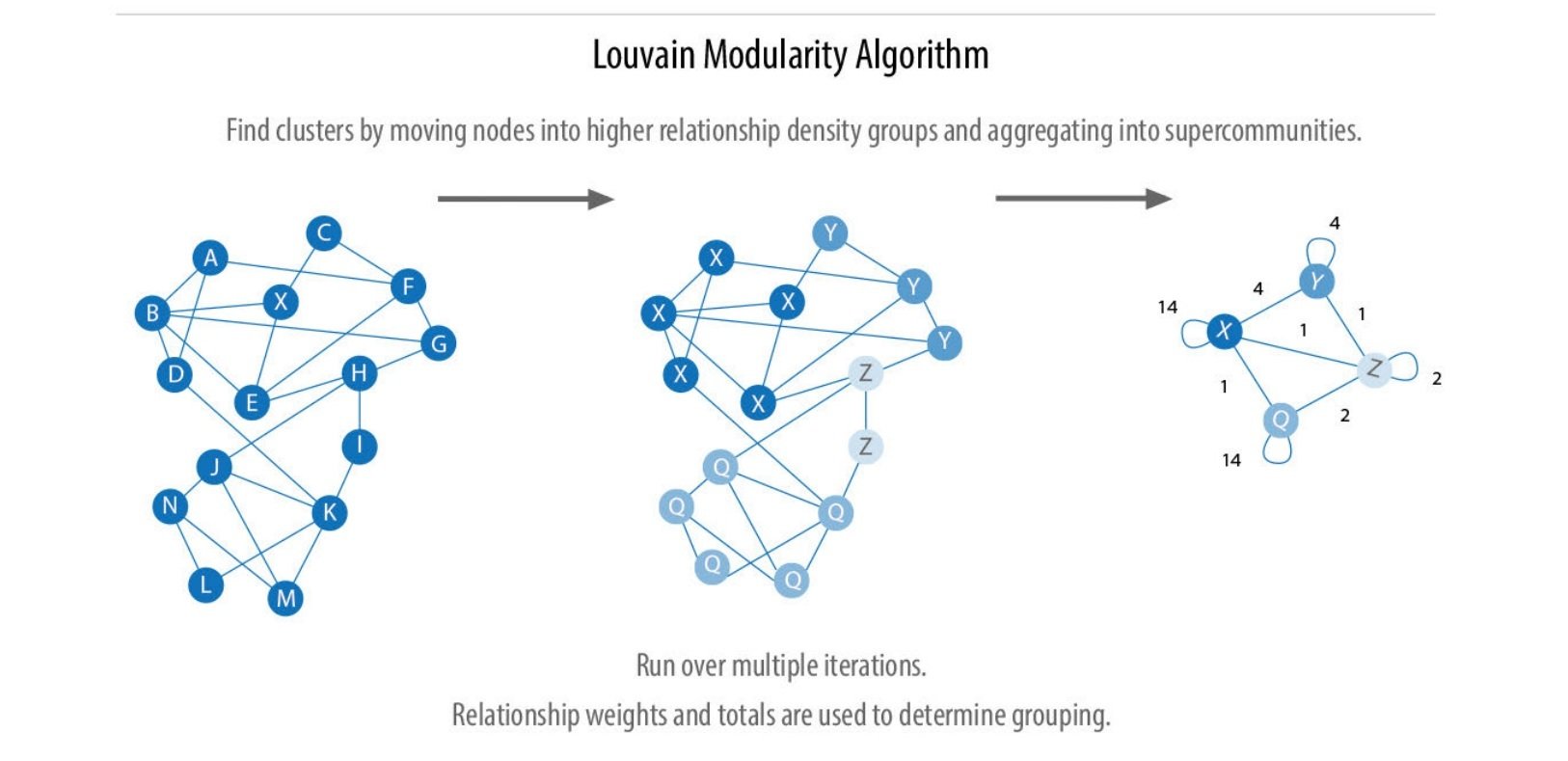
Modularidad de Louvain
Q = \frac{1}{2n}\sum_{ij}[A_{ij} - \frac{K_i K_j}{2n}]\delta(c_i,c_j)
Para:
\( A_{ij} \) Peso entre el vértice \(i\) y el vértice \(j\)
\(K_{ij}\) Es la suma de los pesos que llegan al vértice \(i\) y el vértice \(j\)
\(2n\) Suma de todos los pesos del grafo
\(C_i\) y \(C_j\) son las comunidades en el grafo
\(\delta \) es una función
Antes de Empezar
\Delta Q = [\frac{\sum_{in}+2k_{i,in}}{2m}-(\frac{\sum_{tot}+k_i}{2m})^2]-
[\frac{\sum{in}}{2m}-(\frac{\sum_{tot}}{2m})^2-(\frac{k_i}{2m})^2]
Para:
\(\sum_{in} \) Sumatoria de los pesos dentro de la comunidad
\(\sum_{tot} \) Sumatoria de todos los pesos que conectan a la comunidad
pseudocodigo
Para cada \(v \in V \) :
Asignar \(v \) a una comunidad
Para cada \(v \in V \) :
Escoger un vértice al azar
Calcular \({\Delta Q}\)
Sí \({\Delta Q} > Q\) :
Asignar \(v\) a su vecino
Hacer \(V \) \ \(v \)
Calcular \(Q \)
Rediseñar el Grafo
Ejemplo