Are manifolds useful?
Some basic definitions and related works to planning on manifolds
Outline
- Establishing definitions: manifold, Riemannian metric, homeomorphisms, homotopies, geodesics
- Some related works
- CBiRRT
- GCS
- GGCS
- Some reflections + open questions
Some definitions
please hang with me I promise it's relevant
Manifold definition
A manifold is a topological space that is locally Euclidean
- Def. Locally Euclidean: for any point, we can find a containing open set that is homeomorphic to a subset of R^n
- Def. Homeomorphism: A bijective continuous map between spaces
"stretching one space into another"
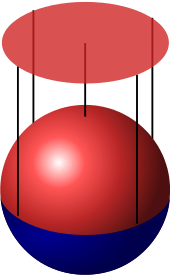
chart of an open set (red) to R^2

everyone's favorite homeomorphism
Manifolds are homeomorphic if they have the same number of "holes"
Manifolds are classified by their fundamental group, which is the fundamental number of ways that you can "walk in a loop" on the object.

Spheres + other objects with "no hole" are null-homotopic, i.e. all loops you can make are homotopic* to a single point.
*homotopy: continuous deformation of a function instead of a space
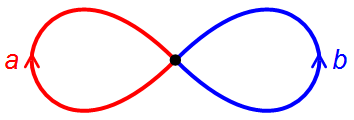
Tori, klein bottles, and coffee mugs all have the fundamental group [a,b].
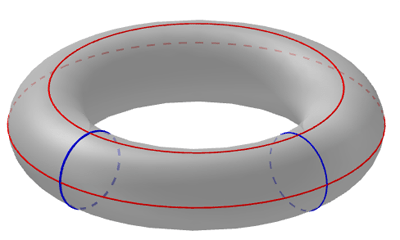

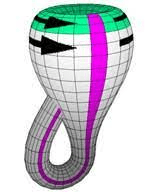
Riemannian manifold definition
A Riemannian manifold is a manifold that is also differentiable at all points (smooth) and equipped with a metric that maps vectors, angles, and distances onto the manifold surface
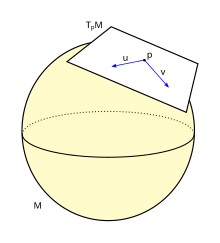
The Riemannian metric must define an inner product between vectors tangent to every point p


the "flat torus" is created by gluing edges of a square: this metric is "stretched" from Euclidean
Geodesics
Under a Riemannian metric, a geodesic is a "length-minimizing curve."
In Euclidean space, these are lines and rays. In different metrics (with different curvature, etc) this may not be the case.
If a subset of a RM is strongly geodesically convex (g-cvx), then the geodesic between any two points is unique. The convexity radius of a point x is how far point y can be before the geodesic starts going "the other way around."
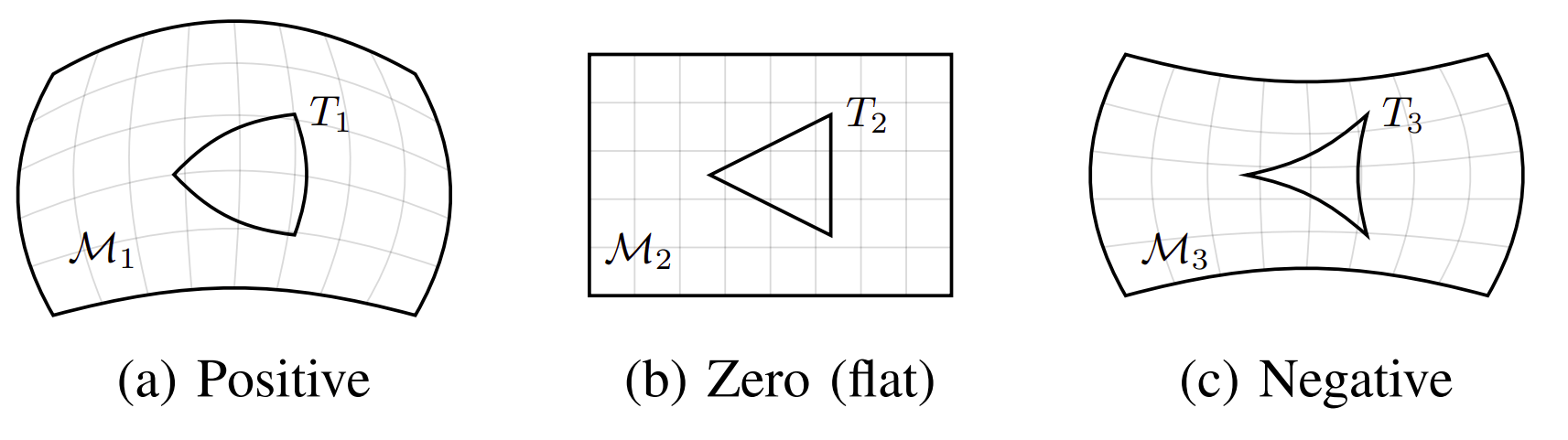
Why this might be relevant / nice for robots
- Configuration-spaces are often Riemannian manifolds
- Many joint and torque constraints are continuous constraints over "patches" of the C-space (rather than point-discontinuities), and their surface is a manifold that can be projected to
- A space that can be planned over may be a homeomorphism away from the actual space. If we require a diffeomorphism, that mapping is continuous + differentiable.
- Objects in the real world (cubes, balls, mugs, limes) are manifolds. A path from point to point on a donut will map to a path on a mug, if we define the homeomorphism between them.
Related works
-
Dmitry + Sidd 2009: CBiRRT (RRT constrained to manifold in C-space)
- acquires manifold by dense sampling + approximation
- GCS: assumes that C-space is Euclidean path-connected (path exists between any two points) -- and can therefore be tiled with convex sets
-
GGCS (Cohn et al. 2023): assumes that C-space is a Riemannian manifold, adapts convex sets to geodesically-convex sets (convex in the metric of the manifold)
- allows expansion to 360-revolute joints and mobile base robots
Planning on manifolds in C-space
Concept: There are different "modes" in a manipulation problem that embody different manifolds in C-space.
CBiRRT
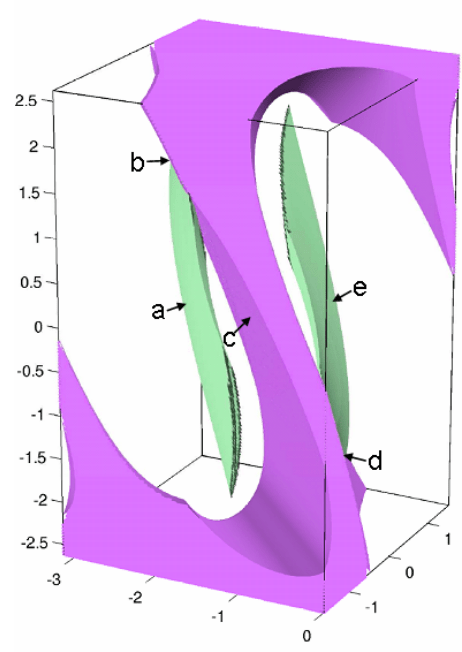
These manifolds intersect at "bridges."
Example: Moving mug from table to table
Purple: torque constraints are valid.
Green: Mug (in hand) is on either table
Goal: Find path from section (a) to section (e), traveling along (c) with bridges at (b) and (d)
CBiRRT

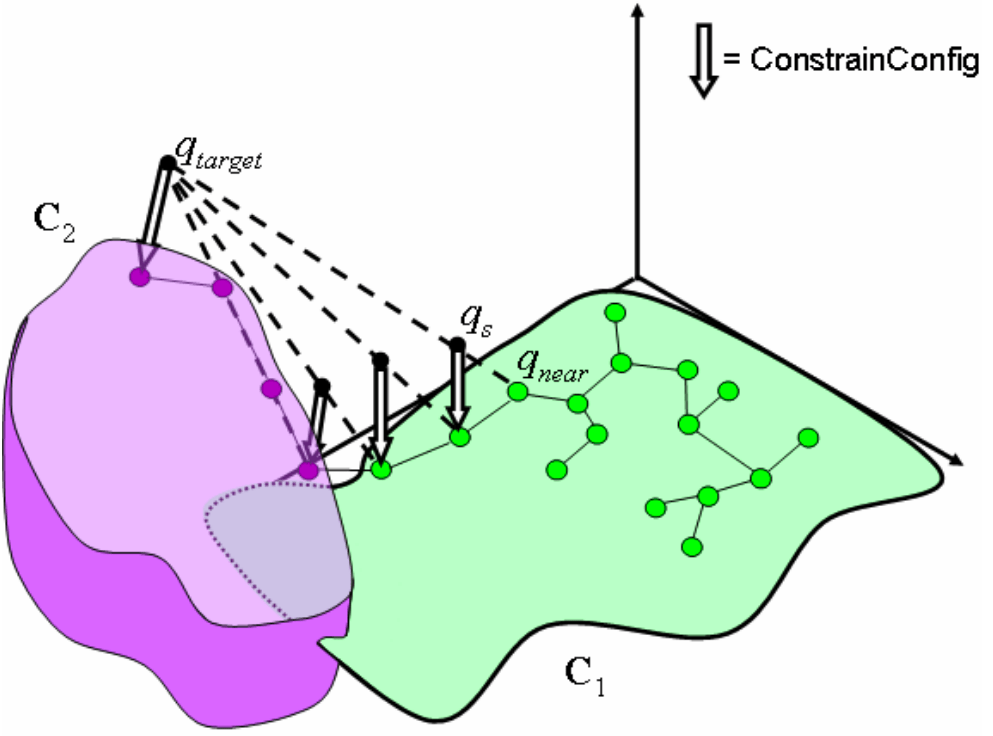
Build two RRT graphs, one in the purple and one in the green, and try to connect their leaf nodes until the line between them in C-space is free
- Project colliding nodes to the nearest constraint surface
Key insight: seeing C-space as containing modes that can be transitioned between, and exploring densely within that mode in the meantime
Manifolds get approximated via dense sampling
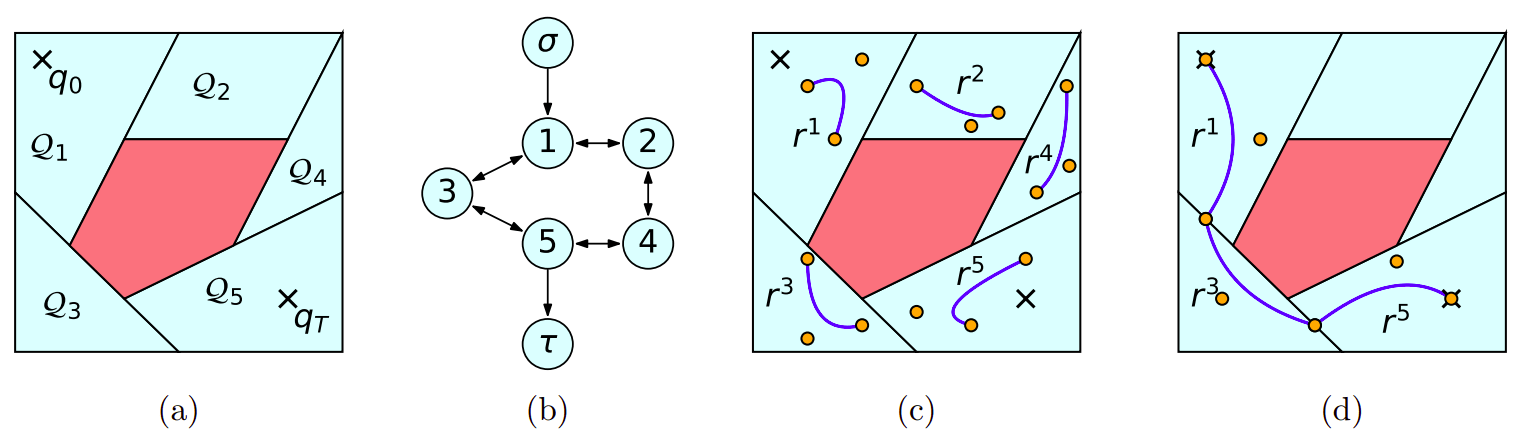
Graph of Convex Sets (GCS)
Concept: Tile the C-space from start to goal with convex sets that are collision/constraint free, then solve for shortest path using MICP and optimize path within nodes
Key insight: Maintaining nearly-optimal performance by using local convexity to optimize path segments. Optimize for Euclidean distance.
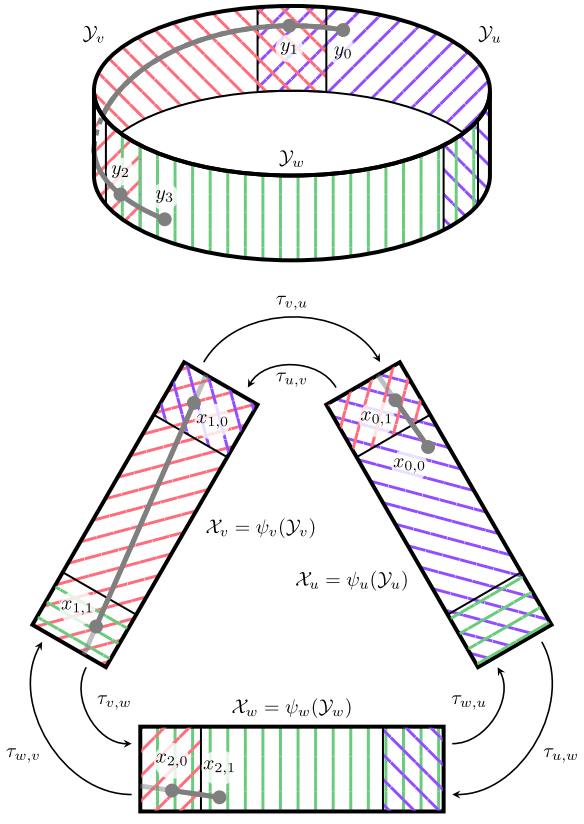
Graph of Geodesically Convex Sets (GGCS)
Concept: Adapt GCS to work on flat* Riemannian manifolds by tiling with geodesically convex sets, solving instead to minimize the geodesic length between start and goal.
*flat RM: a manifold equipped with zero Riemann curvature (locally isometric to Euclidean space, distances and angles are preserved)
Key insight: Adapt to 360-revolute joints and mobile bases by generalizing to Riemannian manifold. Optimize for geodesic distance. A flat manifold is needed.
GGCS: Positive curvature induces nonconvexity
Riemann curvature: Paper analogy.
If the RM has positive Riemann curvature at any point (ex. SO(3)), then the Riemannian distance function will not be g-convex
This disallows solving with GGCS which is a shortest-path problem: the paper could not do ball-joints for example

-
Topological theory gives us guarantees on the existence of homeo/ diffeomorphisms and their properties, but doesn't always give us the closed form solutions for these mappings
-
In practice, we have to do some sampling/exploration to approximate the full manifold that exists (ex. CBiRRT, GGCS) in order to act on it
-
There are mapping schemes that exist for some homeomorphisms, especially to 2D and 1D (think: ways of mapping the globe) using projections etc
- The "local Euclidean" property seems more useful in practice than trying to make a statement on the entire space: it can still be useful to act within some local-Euclidean or g-convex region within a convexity radius
some informal impressions
- Could the modifying the radius of convexity on a Riemannian manifold be used to change the "switch point" of different solutions? (whether the shortest path is one direction or the other)
- What happens when we don't require Riemann flatness (or we transform the solution to a space with positive Riemann curvature)? Can anything be said about the solution anyway?
...and some amateur questions