STL Functions
黃祥陞 @ Sprout 2024 C/C++語法班
Modified from @ Sprout 2023

前言
怎麼去學習 xxx?
- Google "xxx 教學"
- StackOverFlow
- 讀文件!
讀文件的重要性
- 了解細節(實作、複雜度etc.)
- 最準確的資訊
- 當你的問題稀有到沒有人問過

函數名稱
對應的參數型別/回傳型別
函數的說明
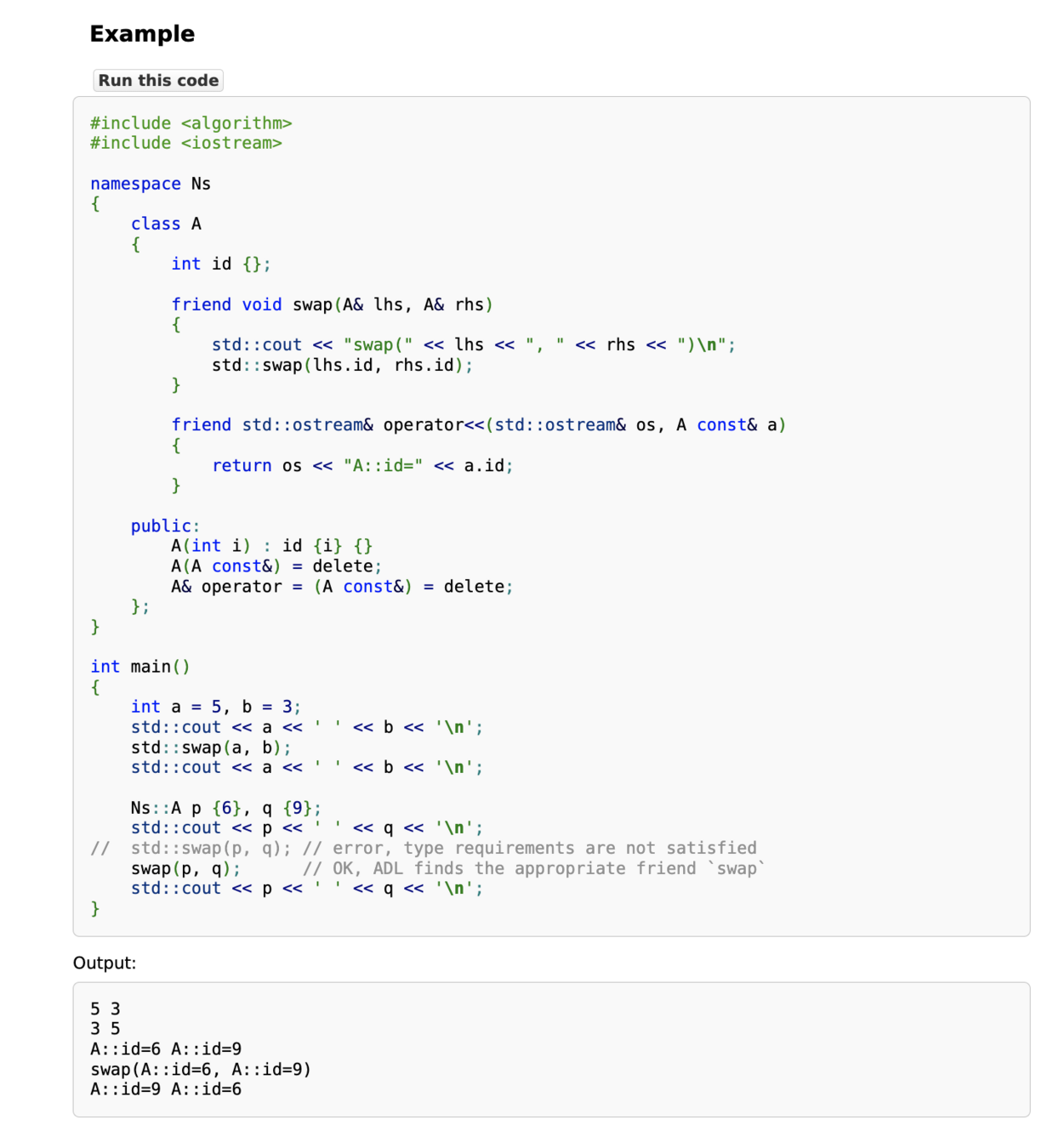
關於這個函數的範例 code
一些技術細節


這堂課絕對無法教完所有C++的 library function。請養成自己查資料的能力
Sort
給你一堆數字N_i,輸出這些數字從小排到大的結果
一些解法
- bubble sort/ insertion sort => 不夠快
- merge sort => 寫起來略麻煩@@
- 其他解法?
std::sort()
- begin: 排序的起點的指標/iterator
- end: 排序的終點的下一個位置的指標/iterator
std::sort(begin, end)也就是在容器的 [begin, end) 的範圍內由小排到大
註: 左閉右開是 STL function 常見的規格
複雜度:O(nlogn)
std::sort 使用了混合了 quicksort 和 O(n^2) 的排序演算法
一些範例
Array
#include<algorithm>
#include<iostream>
int main() {
int arr[] = {4, 8, 7, 6, 3};
int arrsize = 5;
sort(arr, arr + arrsize);
// arr + size 是最後一個元素的「下個位置」的指標
for(int i = 0; i < arrsize; i++) {
cout << arr[i] << " ";
}
cout << endl;
// output: 3 4 6 7 8
}一些範例
Vector
#include<algorithm>
#include<iostream>
#include<vector>
int main() {
vector<int> v({4, 8, 7, 6, 3});
sort(v.begin(), v.end());
// v.end() 是 v 的最後一個元素的「下個位置」的iterator
for(int i = 0; i < arrsize; i++) {
cout << v[i] << " ";
}
cout << endl;
// output: 3 4 6 7 8
}給你一堆數字N_i,輸出這些數字從大排到小的結果
給你一坨學生S_i,輸出這些學生照各科成績和排序的結果
.
.
.
不只是從小排到大
std::sort(begin, end, cmp)cmp: 定義「 a 小於 b 」的函數
由大排到小
bool cmp(int a, int b) {
return a > b;
}不是 int
bool cmp(Student a, Student b) {
return (a.eng + a.math) < (b.eng + b.math);
}
struct Student{
int math, eng;
};補充:Lambda function
當有很多排序的方式 cmp1, cmp2, ...
定義在外面顯得很沒效率
sort(v.begin(), v.end(), [](int a, int b) {
return a > b;
});
vector<int> v;用法:[](參數){函數內容} 即可代表ㄧ個函數
補充:cmp小小眉角
cmp 必須滿足以下性質,否則有機會吃RE:
- cmp(a, a) = false
- cmp(a, b) = true => cmp(b, a) = false
- cmp(a, b) = true and cmp(b, c) = true => cmp(a, c) = true
補充:operator overloading
- 除了用傳入 cmp 的方式來自訂比較方式,也可以透過 overload < 的運算子來達成
struct S {
int math, eng;
}
bool operator < (S a, S b) {
return a.math + a.eng < b.math + b.eng;
}
int main() {
vector<S> v(4);
sort(v.begin(), v.end());
}Search
Search
- 顧名思義,拿來找容器中的元素的函數
- 如果找到,回傳指到該元素的 iterator
- 如果找不到,回傳容器.end() (最後一個元素的下一個位置)
std::find()
- 在容器的 [begin, end) 範圍內尋找 element
- bool : 有沒有 element 這個元素
- 複雜度:O(n)
find(begin, end, element);快,還要更快
如果今天容器的元素已經排序好了,一次查詢可以砍掉一半的可能
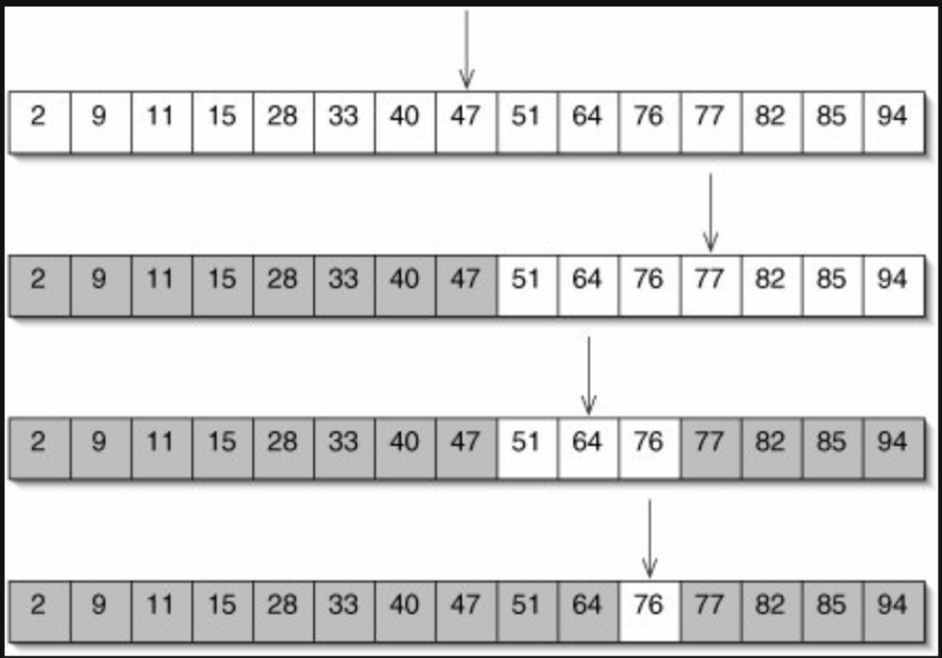
std::binary_search()
std::binary_search(begin, end, element);- 在排序好的容器中尋找第一個為 element 的元素
- 回傳指到該元素的iterator
- 複雜度:O(logn)
std::lower_bound()
std::lower_bound(begin, end, element);- 在排序好的容器中尋找 >= element 的最小元素
- 回傳指到該元素的iterator
- 複雜度:O(logn)
std::upper_bound()
std::upper_bound(begin, end, element);- 在排序好的容器中尋找 > element 的最小元素
- 回傳指到該元素的iterator
- 複雜度:O(logn)
栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({9, 8, 7, 6, 5, 5, 4, 3, 2, 1})
sort(v.begin(), v.end());
cout << *(upper_bound(v.begin(), v.end(), 5)) << endl; // 6
cout << *(lower_bound(v.begin(), v.end(), 5)) << endl; // 5
cout << (find(v.begin(), v.end(), 13)) == v.end() << endl; // 1
}std::nth_element()
std::nth_element(begin, m, end);- 用來在容器中尋找第 n 小的元素
- m 是指向第 n 個元素的 iterator
- 做完後容器的第n個位置就是該元素
- 複雜度:O(n)
註:這個函數的複雜度分析很有趣,推薦有興趣的同學去研究
栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({9, 8, 7, 6, 5, 5, 4, 3, 2, 1})
int rank = 4;
nth_element(v.begin(), v.begin() + rank, v.end());
cout << v[4] << endl; // 4
}Array Related
std::iota()
*(begin + 0) = start
*(begin + 1) = start + 1
.
.
*(begin + i) = start + i
複雜度:O(n)
iota(begin, end, start);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v(5);
iota(v.begin(), v.end(), 4);
for(int i = 0; i < 5; i++) {
cout << v[i] << " ";
}
cout << endl;
// 4, 5, 6, 7, 8
}std::reverse()
- 把容器的 [begin, end) 範圍內元素反轉順序
- 複雜度:O(n)
reverse(begin, end);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({9, 8, 7, 6, 5, 4, 3, 2, 1})
reverse(v.begin(), v.end());
for(int i = 0; i < 9; i++) {
cout << v[i] << " ";
}
cout << endl;
// 1, 2, 3, 4, 5, 6, 7, 8, 9
}std::next_permutation()
- 枚舉下一個字典序的排列
- ex. 123 -> 132 -> 213 -> 231 -> 312 -> 321 -> 123
- 當字典序從最大到最小時,回傳 false ,否則回傳 true
- 複雜度:O(n),amortized O(1)
- 有相同的元素時也可以正常運作
next_permutation(begin, end);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v(3);
iota(v.begin(), v.end(), 1);
do {
for (auto i : v)
cout << i << " ";
cout << "\n";
} while (next_permutation(v.begin(), v.end()));
/*
output:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
*/
}std::prev_permutation()
- 枚舉上一個字典序的排列
- ex. 321 -> 312 -> 231 -> 213 -> 132 -> 123 -> 321
- 當字典序從最小到最大時,回傳 false ,否則回傳 true
- 複雜度:O(n),amortized O(1)
prev_permutation(begin, end);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({3, 2, 1});
do {
for (auto i : v)
cout << i << " ";
cout << "\n";
} while (prev_permutation(v.begin(), v.end()));
/*
output:
3 2 1
3 1 2
2 3 1
2 1 3
1 3 2
1 2 3
*/
}std::fill()
- 在容器的 [begin, end) 範圍內的所有元素設為 element
- 複雜度:O(n)
fill(begin, end, element);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v(5);
fill(v.begin(), v.end(), 48763);
for (auto i : v)
cout << i << " ";
cout << "\n";
// output: 48763, 48763, 48763, 48763, 48763
}std::fill_n()
- 在容器的 [begin, end) 範圍內的所有元素設為 element
- 複雜度:O(n)
fill_n(begin, n, element);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v(5);
fill_n(v.begin(), 5, 48763);
for (auto i : v)
cout << i << " ";
cout << "\n";
// output: 48763, 48763, 48763, 48763, 48763
}std::random_shuffle()
- 將容器 [begin, end) 的元素隨機打亂
- 複雜度:O(n)
random_shuffle(begin, end);std::accumulate()
- 把在容器的 [begin, end) 的元素和加起來再加start
- 複雜度:O(n)
accumulate(begin, end, start);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({4, 8, 7, 6, 3});
cout << accumulate(v.begin(), v.end(), 1) << endl;
// output: 29(4 + 8 + 7 + 6 + 3 + start=1)
}std::partial_sum()
- 把在容器的 [begin, end) 的元素以前綴和存入 begin2
- 複雜度:O(n)
partial_sum(begin, end, begin2);栗子
#include<iostream>
#include<vector>
#include<numeric>
using namespace std;
int main() {
vector<int> v({1, 2, 3, 4, 5});
partial_sum(v.begin(), v.end(), v.begin());
for (auto i : v)
cout << i << "\n";
/*
output:
1
3
6
10
15
*/
}std::unique()
- 容器必須先排序
- 移除 [begin, end) 內重複的元素(移到容器後面)
- 回傳指向最後一個非重複元素的下一個位置的 iterator
unique(begin, end);栗子
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
vector<int> v({1, 2, 3, 2, 3, 1});
sort(v.begin(), v.end());
auto tmp = unique(v.begin(), v.end()); // v.begin() + 3
v.resize(tmp - v.begin()); // aka v.resize(3)
// v.erase(tmp, v.end());
for (auto i : v)
cout << i << " ";
cout << "\n";
// output: 1, 2, 3
}練習題時間
OJ #153 (不算分)
OJ #4949 (算分)
OJ #153
題目:
給定一個排序好且元素相異的字串,依照字典序輸出所有排列
- 如何枚舉所有字串?
- 如何知道什麼時候枚舉完?
OJ #153
題目:
給定一個排序好且元素相異的字串,依照字典序輸出所有排列
- 如何枚舉所有字串?
- 如何知道什麼時候枚舉完?
std::next_permutation()
next_permutation() == false
do {
輸出字串
枚舉下一個排列
} while(還沒枚舉完);
Using next_permutation
#include <iostream>
#include <cstring>
using namespace std;
char a[26], ans[26];
bool used[26];
void dfs(int cnt, int len) {
if (cnt == len) {
ans[cnt] = '\0';
cout << ans << '\n';
return;
}
for (int i = 0; i < len; i++)
if (!used[i]) {
used[i] = 1, ans[cnt] = a[i];
dfs(cnt + 1, len);
ans[cnt] = 0, used[i] = 0;
}
}
int main() {
cin >> a;
int len = strlen(a);
dfs(0, len);
}Recursive Solution
OJ #4949
題目:
給定大小為 N 的陣列 a, Q 筆詢問。每筆詢問會有
L, R,輸出滿足 L ≤ a_i ≤ R 的 a_i 的數量。
先不管 STL,你會怎麼做?
OJ #4949 subtask 1
對於每筆詢問,我們都掃描一次陣列去數滿足L ≤ a_i ≤ R 的 a_i 的數量。
用兩層迴圈即可解決
while(還有詢問) {
for i in v {
if 滿足條件 {
數量+1
}
}
輸出數量
}複雜度:O(NQ)
N, Q ≤ 10^6
=> TLE for subtask 2
OJ #4949 subtask 2
觀察:
如果先把陣列排序好
滿足條件的數量: 1 + 最後一個滿足的元素位置 - 第一個滿足的元素的位置
1 + 最後一個滿足的位置 : 大於 R 的第一個元素
第一個滿足的位置: 大於等於 L 的第一個元素
OJ #4949 subtask 2
觀察:
如果先把陣列排序好
滿足條件的數量: 1 + 最後一個滿足的元素位置 - 第一個滿足的元素的位置
1 + 最後一個滿足的位置 : 大於 R 的第一個元素
第一個滿足的位置: 大於等於 L 的第一個元素
lower_bound() /upper_bound()
把陣列排序
while(還有詢問) {
a = 找到大於 R 的第一個位置
b = 找到大於等於 L 的第一個位置
輸出 a - b
}複雜度:O(QlogN)
因為 lower_bound/upper_bound 使用二分搜尋法
The End
還有一些練習題
回家作業(算分)
OJ #1111
建議練習題(不算分)
OJ # 804
OJ #448
OJ #2024