VIDEOJUEGOS


PROBOTS 2019

Introducción a lógica

¿Cuando empezó la computación?


Charles Babbage (1791 - 1871)


Introducción a lógica

Prehistoria de la computación

Máquina diferencial. Idea: 1786. Construcción: 1822. Finalización: 1991

R = 9x5 + 5x4 + x3 + 7x2 + 4x + 41

Introducción a lógica

Prehistoria de la computación


Máquina analítica: 1830

Introducción a lógica

Prehistoria de la computación


Tarjetas perforadas

Introducción a lógica

Prehistoria de la computación


Ada Lovelace

Introducción a lógica

Prehistoria de la computación

Pequeña sección de la máquina analítica

Introducción a lógica

Bits


No energía = Bajo voltaje = 0 = Falso = .F.


Energía = Alto voltaje = 1 = Verdadero = .V.


Introducción a lógica

compuertas lógicas


NOT = NO = Invertido = - = ! = ¬

Tabla de verdad puerta NOT
Entrada A Salida \overline{A}
0
1
1
0

Introducción a lógica

compuertas lógicas


OR = O = +

Tabla de verdad puerta OR
Entrada A Entrada B Salida A \or B
0
0
0
0
1
1
1
0
1
1
1
1

Introducción a lógica

compuertas lógicas


AND = Y = *

Tabla de verdad puerta AND
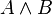
Entrada A Entrada B Salida A \and B
0
0
0
0
1
0
1
0
0
1
1
1

Introducción a lógica

Precedencia de los operadores lógicos


  1. NOT
  2. AND
  3. OR

Introducción a lógica

viéndolo a través de un juego


ALU dentro del juego

Introducción a lógica

Práctica 1

  1. 0 OR 1 = ?
  2. 1 AND 1 = ?
  3. NOT 1 = ?
  4. 1 AND 1 OR 0 = ?
  5. NOT .V. OR .V. AND .V. = ?
  6. .F. AND .F. AND .V. OR NOT .F. = ?

Introducción a lógica

Resolución Práctica 1

Ejercicio 1: 0 OR 1 = ?


image/svg+xml0 OR 11

Introducción a lógica

Resolución Práctica 1

Ejercicio 2: 1 AND 1 = ?


image/svg+xml1 AND 11

Introducción a lógica

Resolución Práctica 1

Ejercicio 3: NOT 1 = ?


image/svg+xmlNOT 11

Introducción a lógica

Resolución Práctica 1

Ejercicio 4: 1 AND 1 OR 0 = ?


1       AND     1      OR      0

image/svg+xml



1

image/svg+xml



1

Introducción a lógica

Resolución Práctica 1

Ejercicio 5: NOT .V. OR .V. AND .V. = ?


NOT         .V.        OR         .V.       AND     .V.

image/svg+xml



.F.

image/svg+xml


.V.

image/svg+xml

.V.

Introducción a lógica

Agrupación de operaciones

()

[]

{}


Ejemplo:

(.V. OR .F.) AND .V.

NOT [(.V. OR .F.) AND .V.]

{ NOT [(.V. OR .F.) AND .V.]} AND .V.

Introducción a lógica

operadores relacionales

  • ==   Igual (=):             ej. 5 == 6 =   .F.
  • !=     Distinto (<>)  ej.  10 != 11 =  .V.
  • <       Menor               ej:  5 < 3 = .F.
  • >       Mayor               ej:  5 > 3 = .V.
  • <=   Menor o igual
  • >=   Mayor o igual
  • OR
  • AND
  • NOT


Introducción a lógica

Práctica 2

  1. (NOT .V. OR .V.) AND .V. = ?
  2. NOT [(.V. OR .F.) AND .V.]

  3. { NOT [(.V. OR .F.) AND .V.]} AND .V.

  4. 6 >= 6 AND 5 == 6
  5. NOT (21 < 12) OR .V.
  6. (2 > 3 OR 5 != 5) == [NOT (5>6)]
  7. (5 <= 6) AND [.V. OR (.F. AND 5 > 6)]
  8. (6 >= 6 AND 5 == 6) OR {(2 > 3 OR 5 != 5) == [NOT (5>6)]}
Made with Slides.com