DNA sequence motif identification using Gibbs sampling

By Rasa, Maxandre, Guillermo

Outline

Regulatory motifs in DNA sequences

Gibbs sampling

DNA motif model

Known motif length

Unknown motif length

Allowing sequences without the motif

Accounting for phylogenetic relations

Directly inferring K

Regulatory motifs

Regulatory motifs are short (5-30 bp) DNA regions that are located near genes to influence their level of expression.

 

Since these regions are functionally important, they are considered to be highly conserved between species.

 

So, to detect them, we can look for highly conserved segments in a set of orthologous genes.

 

Bayesian inference

What is the "best" parameter given data?

  • Posterior mean
  • Maximum likelihood
  • Maximum information

A way to approximate these is to sample the posterior distribution

Bayes theorem

P(\text{params}\mid \text{data}) = \frac{P(\text{data}\mid\text{params})P(\text{params})}{P(\text{data})}
P(params∣data)=P(data∣params)P(params)P(data)P(\text{params}\mid \text{data}) = \frac{P(\text{data}\mid\text{params})P(\text{params})}{P(\text{data})}

likelihood

prior

model

DNA motifs model

Motif representation

M= \left( \begin{array}{cccc} M_A^{(1)} & M_A^{(2)} & ...& M_A^{(K)} \\ M_C^{(1)} & M_C^{(2)} & .. & M_C^{(K)} \\ M_G^{(1)} & M_G^{(2)} & ... & M_G^{(K)} \\ M_T^{(1)} & M_T^{(2)} & ... & M_T^{(K)} \end{array} \right)
M=(MA(1)MA(2)...MA(K)MC(1)MC(2)..MC(K)MG(1)MG(2)...MG(K)MT(1)MT(2)...MT(K))M= \left( \begin{array}{cccc} M_A^{(1)} & M_A^{(2)} & ...& M_A^{(K)} \\ M_C^{(1)} & M_C^{(2)} & .. & M_C^{(K)} \\ M_G^{(1)} & M_G^{(2)} & ... & M_G^{(K)} \\ M_T^{(1)} & M_T^{(2)} & ... & M_T^{(K)} \end{array} \right)

Background model

G= \left( \begin{array}{c} G_A \\ G_C \\ G_G \\ G_T \end{array} \right)
G=(GAGCGGGT)G= \left( \begin{array}{c} G_A \\ G_C \\ G_G \\ G_T \end{array} \right)

DNA motifs model

Starting positions of each motif

s= \left( \begin{array}{c} s_1 \\ s_2 \\ \vdots \\ s_N \end{array} \right)
s=(s1s2⋮sN)s= \left( \begin{array}{c} s_1 \\ s_2 \\ \vdots \\ s_N \end{array} \right)

Total number of sequences

DNA motif model

Probability of sequence

P(X_1,...,X_L|M,s) = \prod\limits_{j=1}^{s} G_{X_j} \prod\limits_{j=s}^{s+K-1} M_{X_j}^{j-s+1} \prod\limits_{j=s+K-1}^{s} G_{X_j}
P(X1,...,XL∣M,s)=∏j=1sGXj∏j=ss+K−1MXjj−s+1∏j=s+K−1sGXjP(X_1,...,X_L|M,s) = \prod\limits_{j=1}^{s} G_{X_j} \prod\limits_{j=s}^{s+K-1} M_{X_j}^{j-s+1} \prod\limits_{j=s+K-1}^{s} G_{X_j}
P(\{X\}\mid M,s) = \prod\limits_{i=1}^N P(X^{(i)}_1,...,X^{(i)}_L|M,s)
P({X}∣M,s)=∏i=1NP(X1(i),...,XL(i)∣M,s)P(\{X\}\mid M,s) = \prod\limits_{i=1}^N P(X^{(i)}_1,...,X^{(i)}_L|M,s)

Probability over all sequences

P(s\mid M)
P(s∣M)P(s\mid M)

uniform,

because posterior is a simple multinoulli

P(M^{(k)} \mid s) \sim Dirichlet(\alpha)
P(M(k)∣s)∼Dirichlet(α)P(M^{(k)} \mid s) \sim Dirichlet(\alpha)

We choose the Dirichlet distribution because it is conjugate to the multinomial likelihood

P(M^{(k)}\mid\{X\},s) \sim Dirichlet(\alpha + f(k,s,\{X\})
P(M(k)∣{X},s)∼Dirichlet(α+f(k,s,{X})P(M^{(k)}\mid\{X\},s) \sim Dirichlet(\alpha + f(k,s,\{X\})

Priors and posteriors

f(k,s,\{X\})
f(k,s,{X})f(k,s,\{X\})

Text

is the count of each base at position k of motif

Gibbs sampling

A Markov Chain Monte Carlo method for sampling posterior distributions in Bayesian inference

Problem

P(M,s\mid \{X\}) = \frac{P(\{X\}\mid M,s)P(M,s)}{P(\{X\})}
P(M,s∣{X})=P({X}∣M,s)P(M,s)P({X})P(M,s\mid \{X\}) = \frac{P(\{X\}\mid M,s)P(M,s)}{P(\{X\})}

Problem:

P(\{X\}\mid M,s) P(M,s)
P({X}∣M,s)P(M,s)P(\{X\}\mid M,s) P(M,s)

has a complicated form

so can't compute

P(\{X\}) = \sum_{M,s} P(\{X\}\mid M,s) P(M,s)
P({X})=∑M,sP({X}∣M,s)P(M,s)P(\{X\}) = \sum_{M,s} P(\{X\}\mid M,s) P(M,s)

so can't sample posterior

Solution:

Gibbs sampling

P(M \mid \{X\}, s) = \frac{P(\{X\}\mid M,s) P(M\mid s)}{p(\{X\}\mid s)}
P(M∣{X},s)=P({X}∣M,s)P(M∣s)p({X}∣s)P(M \mid \{X\}, s) = \frac{P(\{X\}\mid M,s) P(M\mid s)}{p(\{X\}\mid s)}
P(s\mid \{X\},M) = \frac{P(\{X\}\mid M,s) P(s \mid M)}{P(\{X\}\mid M)}
P(s∣{X},M)=P({X}∣M,s)P(s∣M)P({X}∣M)P(s\mid \{X\},M) = \frac{P(\{X\}\mid M,s) P(s \mid M)}{P(\{X\}\mid M)}

The key: these have easy functional forms!

mainly because the domains are simpler

sample M

sample s

\sim
∼\sim
\sim
∼\sim

The sequence of M and s produced is assured to converge to samples from the full posterior

P(M,s\mid \{X\})
P(M,s∣{X})P(M,s\mid \{X\})

Known motif length

As a simplification, let's start by assuming the length K of the regulatory motif we're looking for is known.

Challenge:

Maximising the quality of our candidate regulatory motif 

One parameter can vary:

a that determines our prior belief on M, of the form:

 

\hat{M}
M^\hat{M}
Dirichlet(M^{(SequencePosition)}|a*\mathbb{1}_{4\times1})
Dirichlet(M(SequencePosition)∣a∗14×1)Dirichlet(M^{(SequencePosition)}|a*\mathbb{1}_{4\times1})

Challenge:

Maximising the quality of our candidate regulatory motif 

How do we define the quality of a candidate regulatory motif?

 

Two possibilities:

1) it is a lot more likely that it is a regulatory motif than not;

2) it stands out in a sequence, i.e. it has a high information content or, equivalently, a low information entropy.

\hat{M}
M^\hat{M}

Challenge:

Maximising the quality of our candidate regulatory motif 

...each run of the Gibbs sampler will produce:

1) a maximum likelihood estimate for M;

 

2) a minimum entropy estimate for M.

\hat{M}
M^\hat{M}

As a result, bear in mind that...

...and a mean of the Ms generated at each iteration of the algorithm (which are sampled from their posterior distribution, as we said previously).

Challenge:

Maximising the quality of our candidate regulatory motif 

And so what are we trying to optimise with a?

 

Two possibilities: find a such that

1) we find the M with maximum likelihood among the different maximum likelihood estimates of M;

 

2) we find the M with minimum entropy among the minimal entropy estimates of M.

\hat{M}
M^\hat{M}

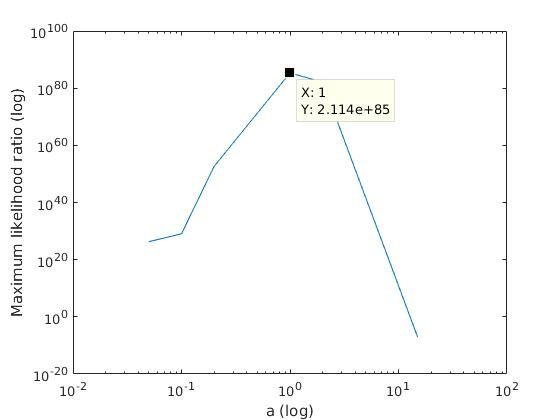
Solution

 

With K = 10:

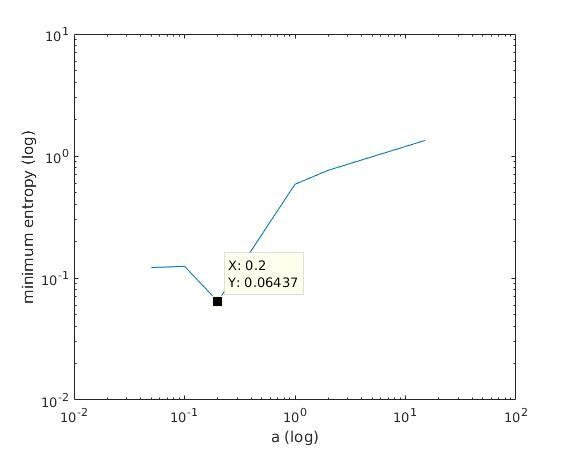
=> M is best

when a ≈ 0.2

With K = 12:

=> M is best

when a ≈ 0.1

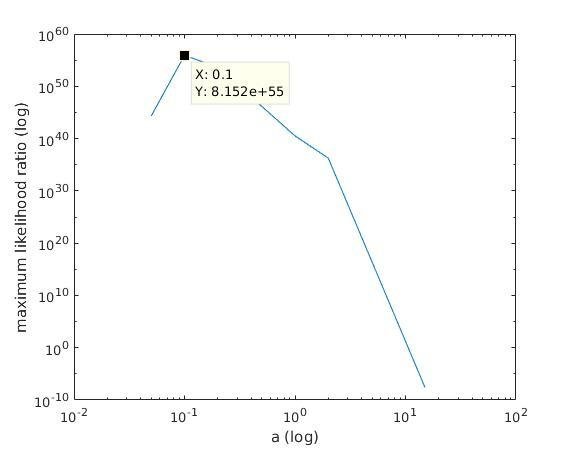
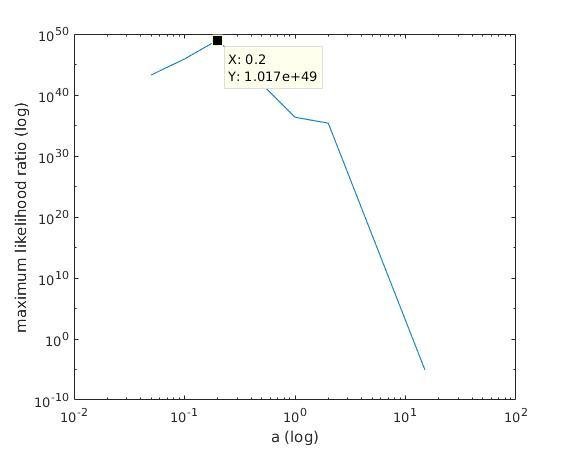
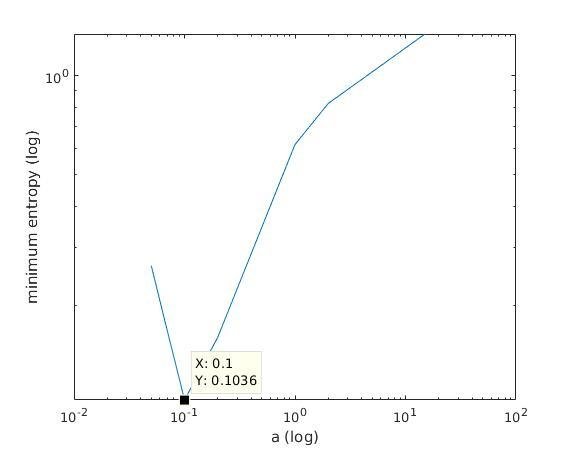
Maximum entropy (log)

Maximum likelihood ratio (log)

Maximum entropy (log)

a (log)

a (log)

a (log)

a (log)

Maximum likelihood ratio (log)

Results

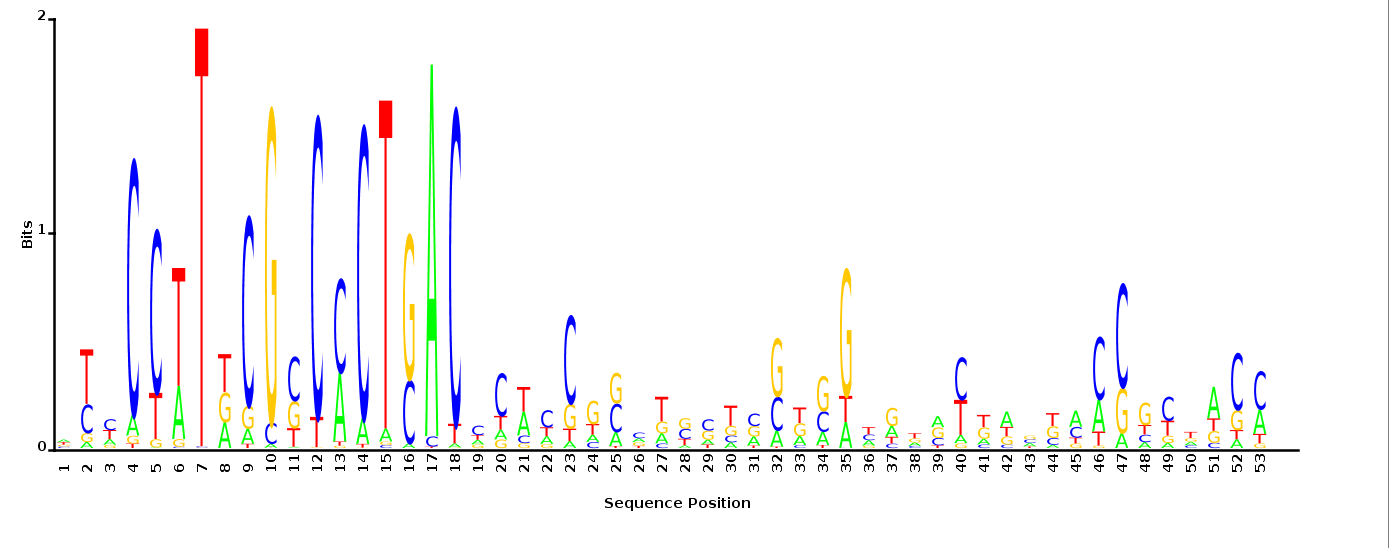
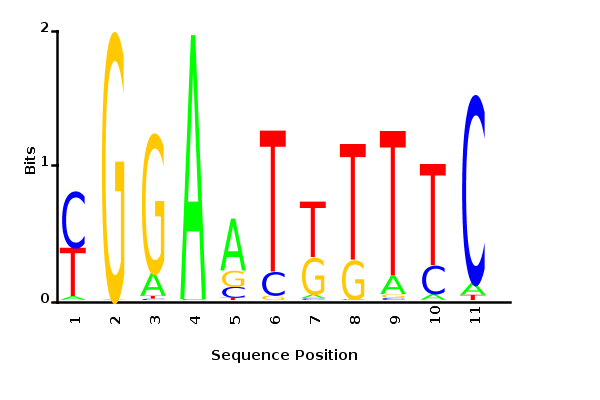
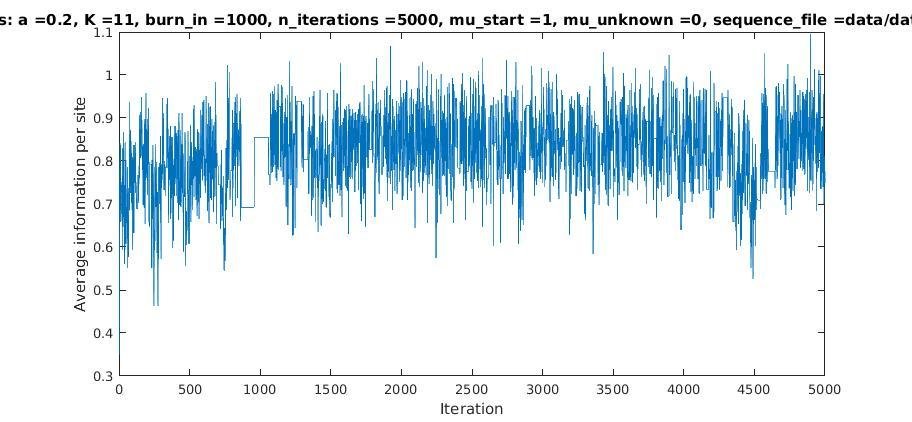
With K = 10 and a = 0.2:

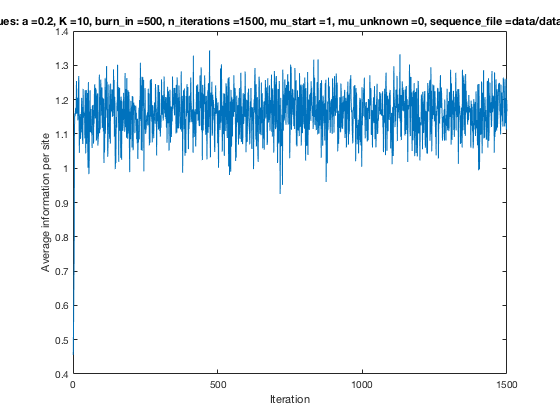
The Gibbs sampler seems to converge very quickly to a motif :

Depending on the criteria we use to select      three are possible:

\hat{M}
M^\hat{M}

maximum likelihood

minimum entropy

posterior mean

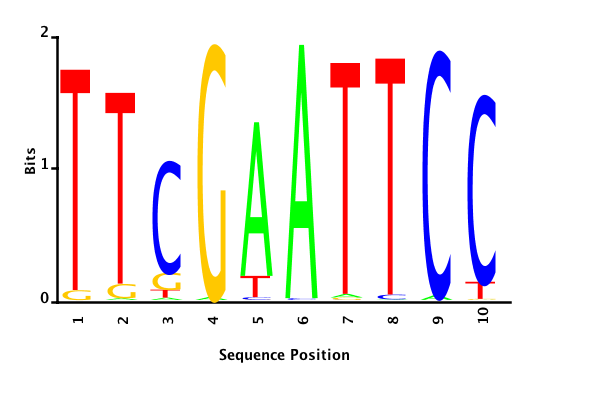
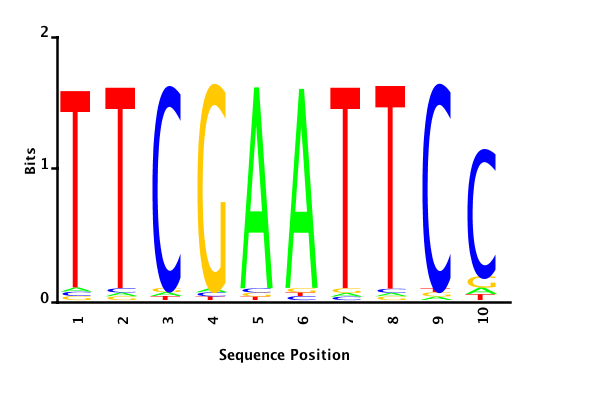
Results

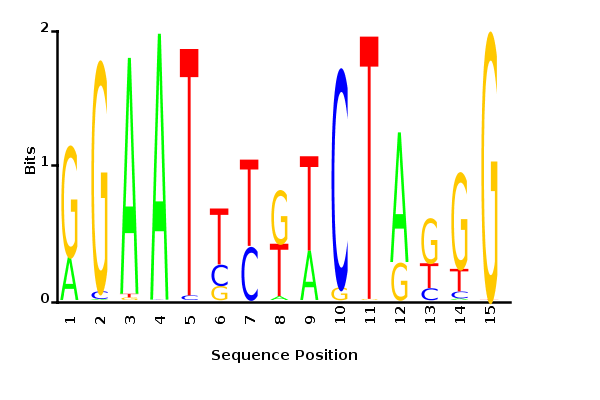
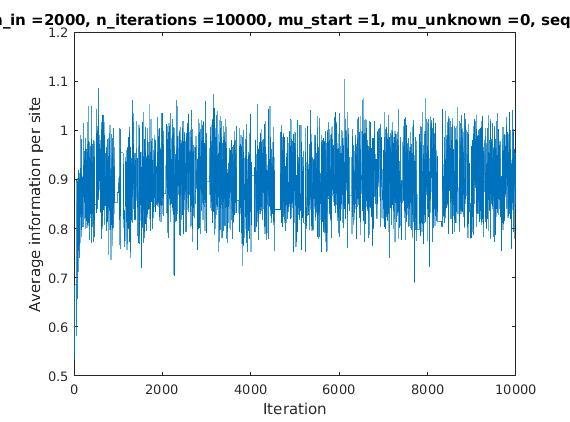
With K = 12 and a = 0.1:

The Gibbs sampler also seems to converge quickly to a motif :

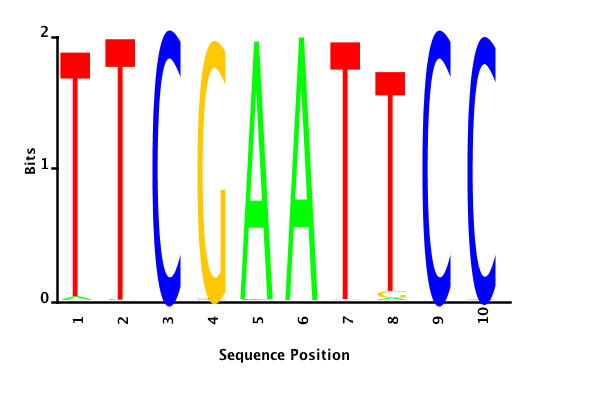
Depending on the criteria we use to select      three are possible:

\hat{M}
M^\hat{M}

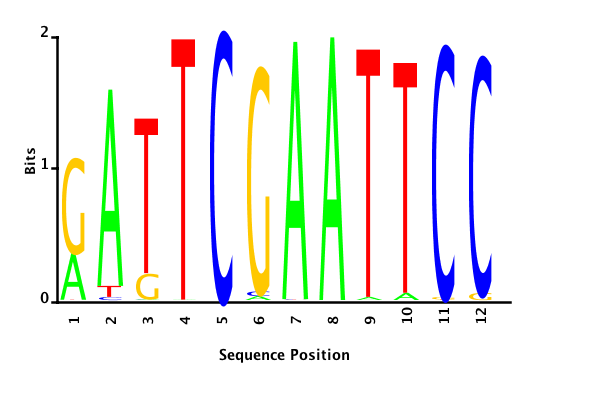
maximum likelihood

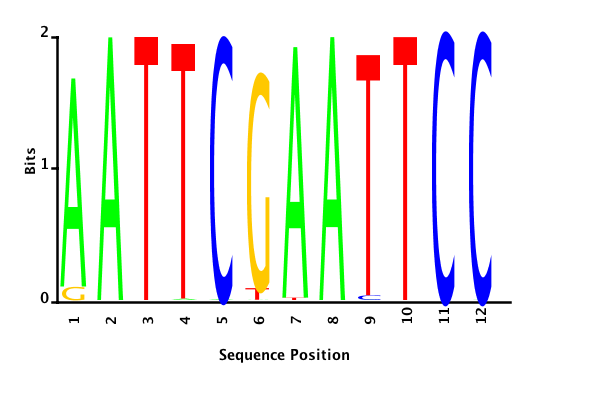
minimum entropy

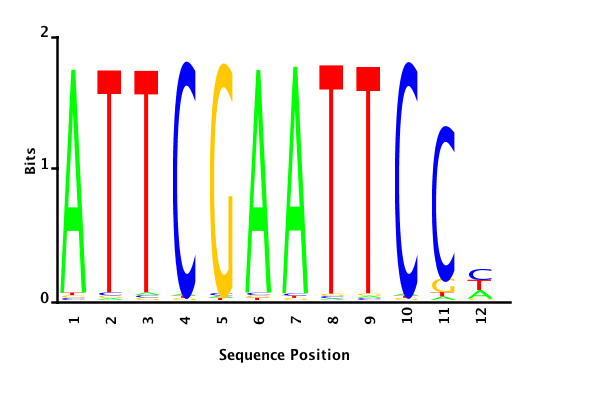
posterior mean

Unknown motif length

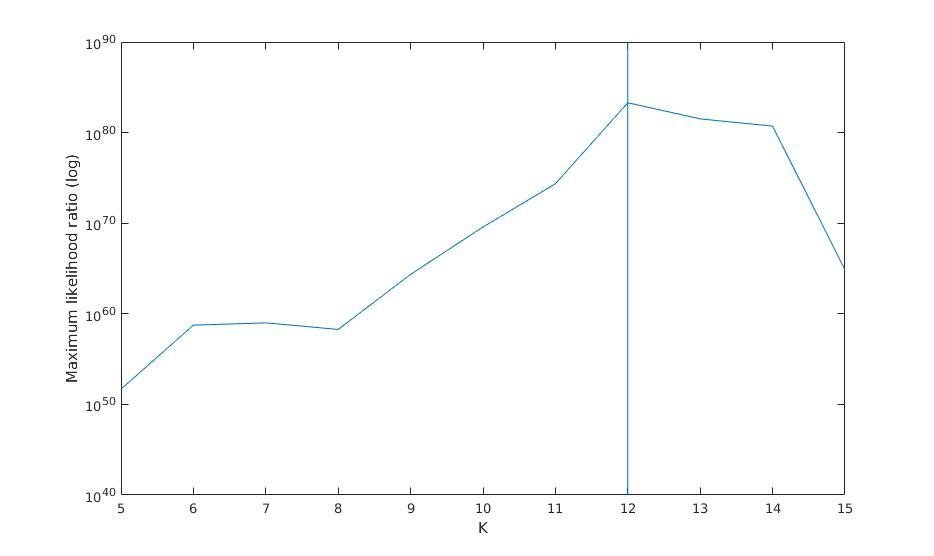
Maximum likelihood ratio versus K

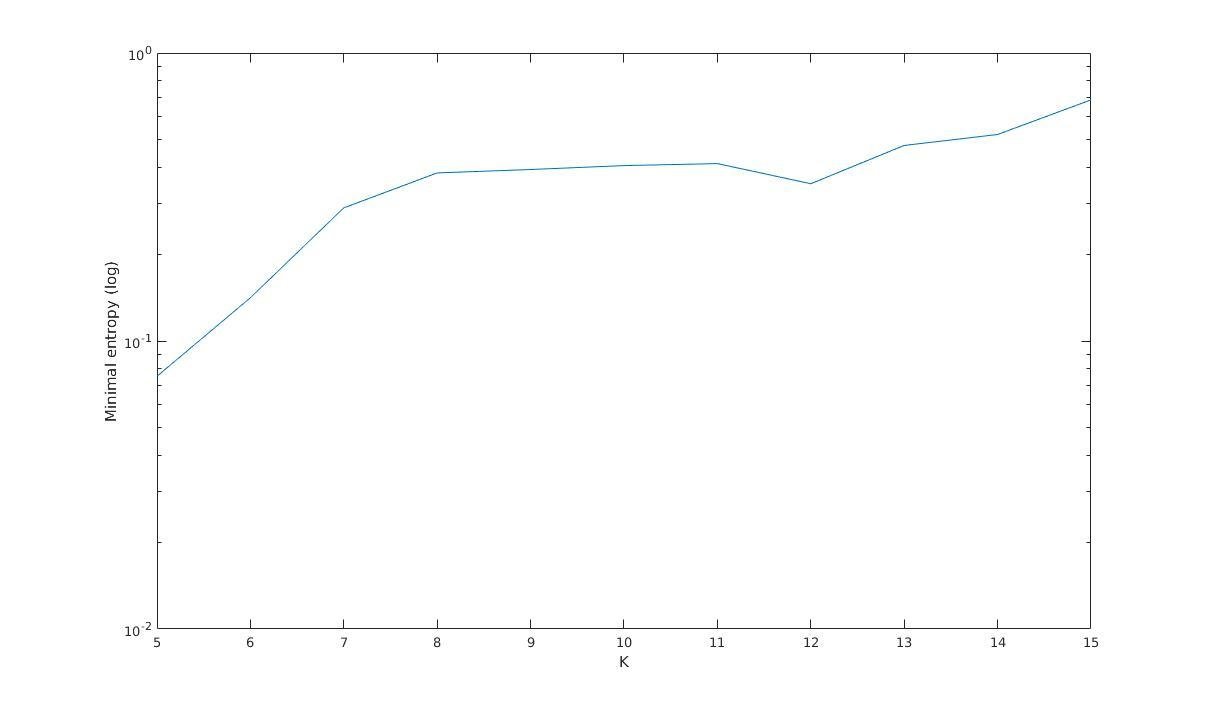
Minimal entropy versus K

Minimal entropy (log)

K

K

Maximum likelihood ratio (log)

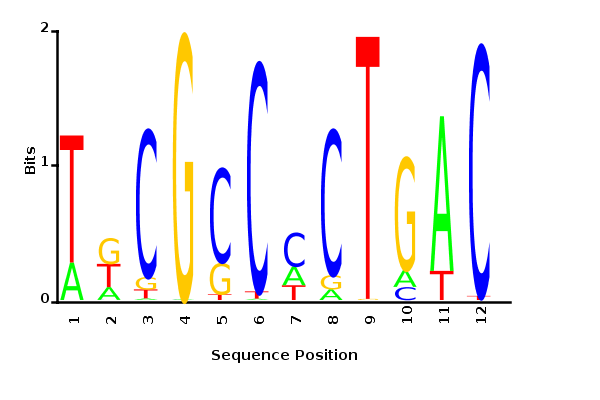
Maximum likelihood PWM

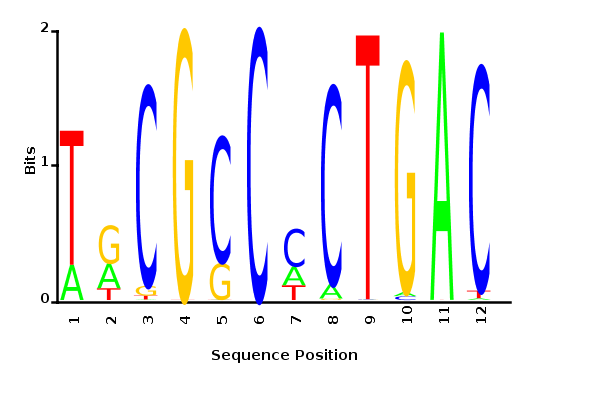
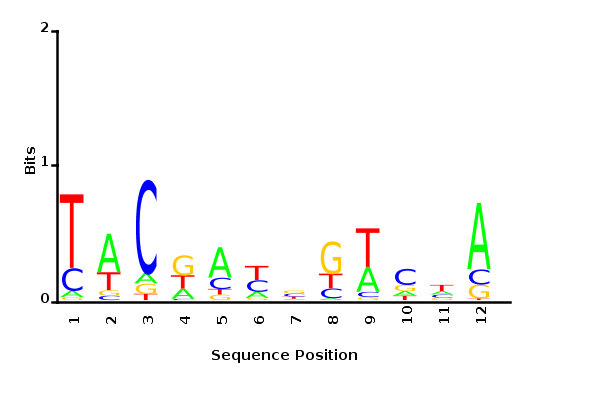
Minimum entropy PWM

Posterior mean PWM

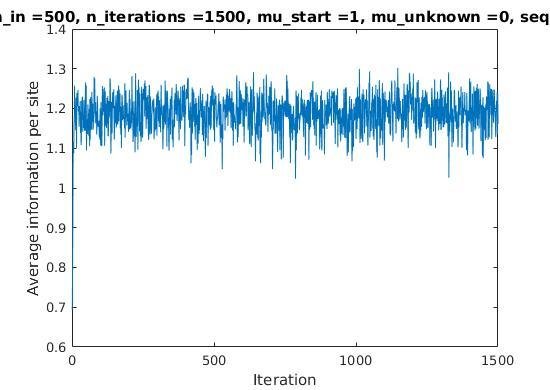
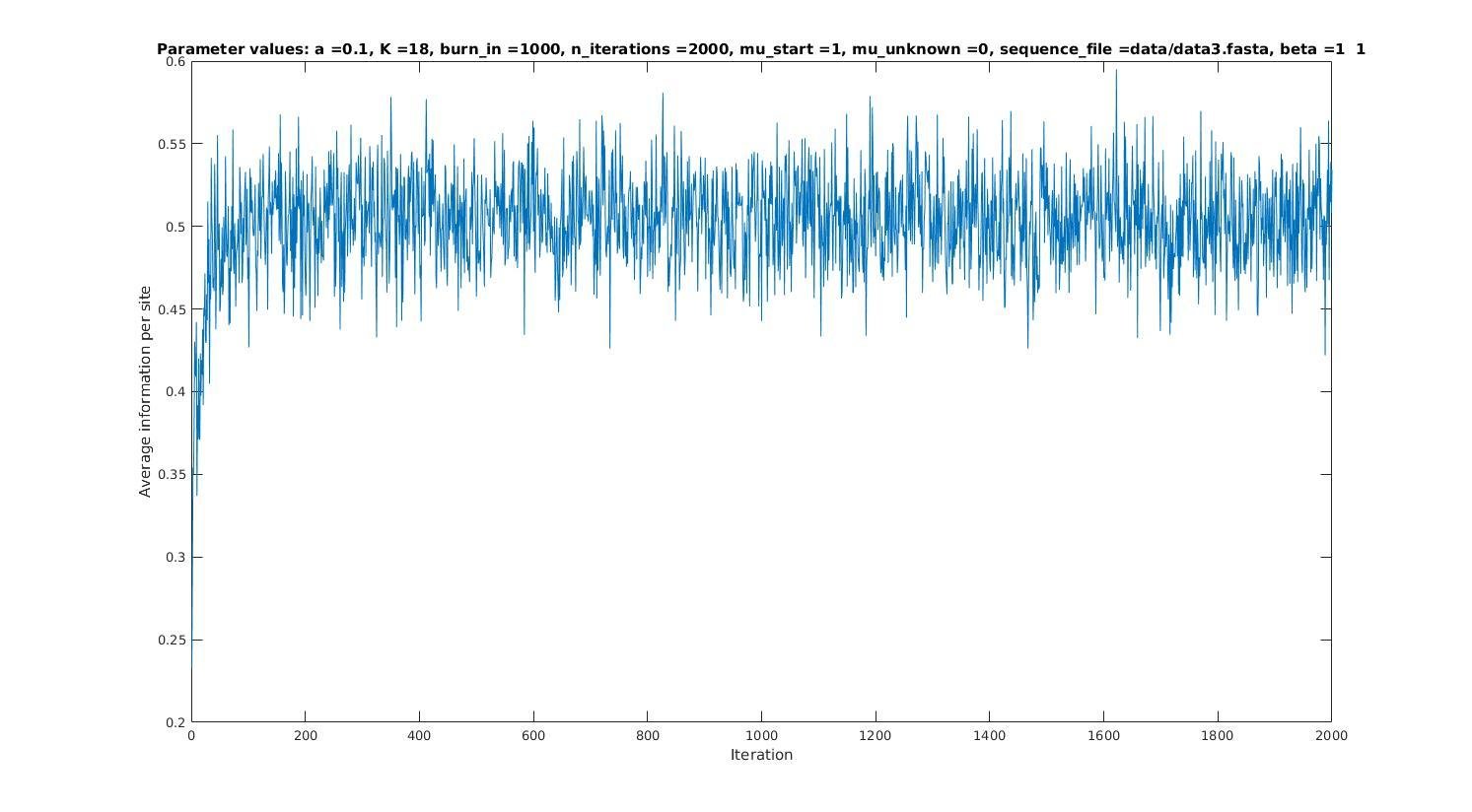
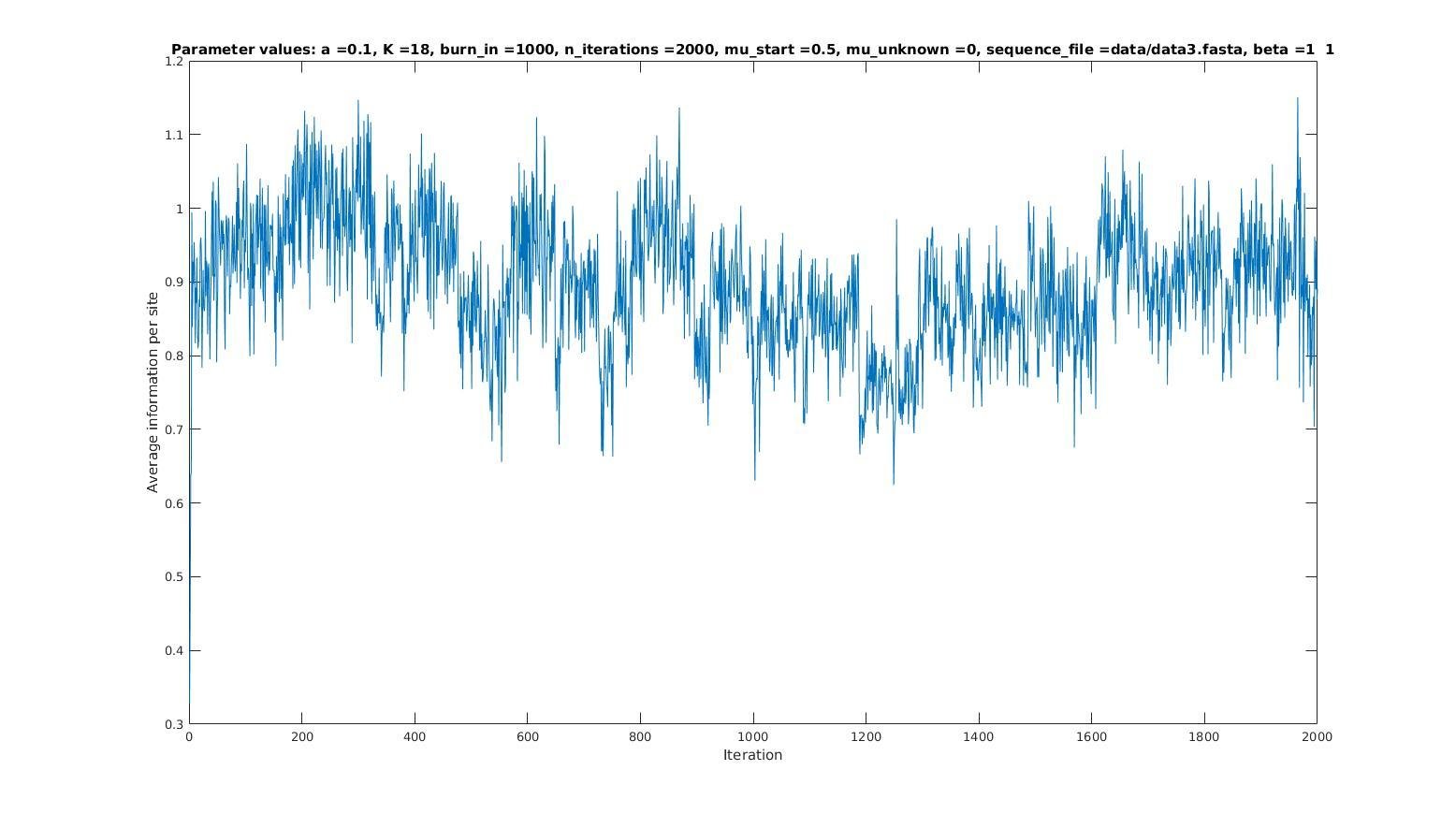
Iterations

Average information

per site

Allowing sequences without the motif

\mu
μ\mu

- probability of any sequencing containing a motif

z_i = \begin{cases} 1, \\ 0, \end{cases}
zi={1,0,z_i = \begin{cases} 1, \\ 0, \end{cases}

if sequence i contains a motif;

otherwise.

z_i = 0
zi=0z_i = 0

Set

\frac{(L_i - K +1)(1-\blue{\mu})}{(L_i - K +1)(1-\blue{\mu}) + \blue{\mu} \sum_n \pi_n}
(Li−K+1)(1−μ)(Li−K+1)(1−μ)+μ∑nπn\frac{(L_i - K +1)(1-\blue{\mu})}{(L_i - K +1)(1-\blue{\mu}) + \blue{\mu} \sum_n \pi_n}

with prob

\mu = 0.3
μ=0.3\mu = 0.3
\mu = 0.5
μ=0.5\mu = 0.5
\mu = 0.8
μ=0.8\mu = 0.8
\frac{4}{33}
433\frac{4}{33}
\frac{11}{33}
1133\frac{11}{33}

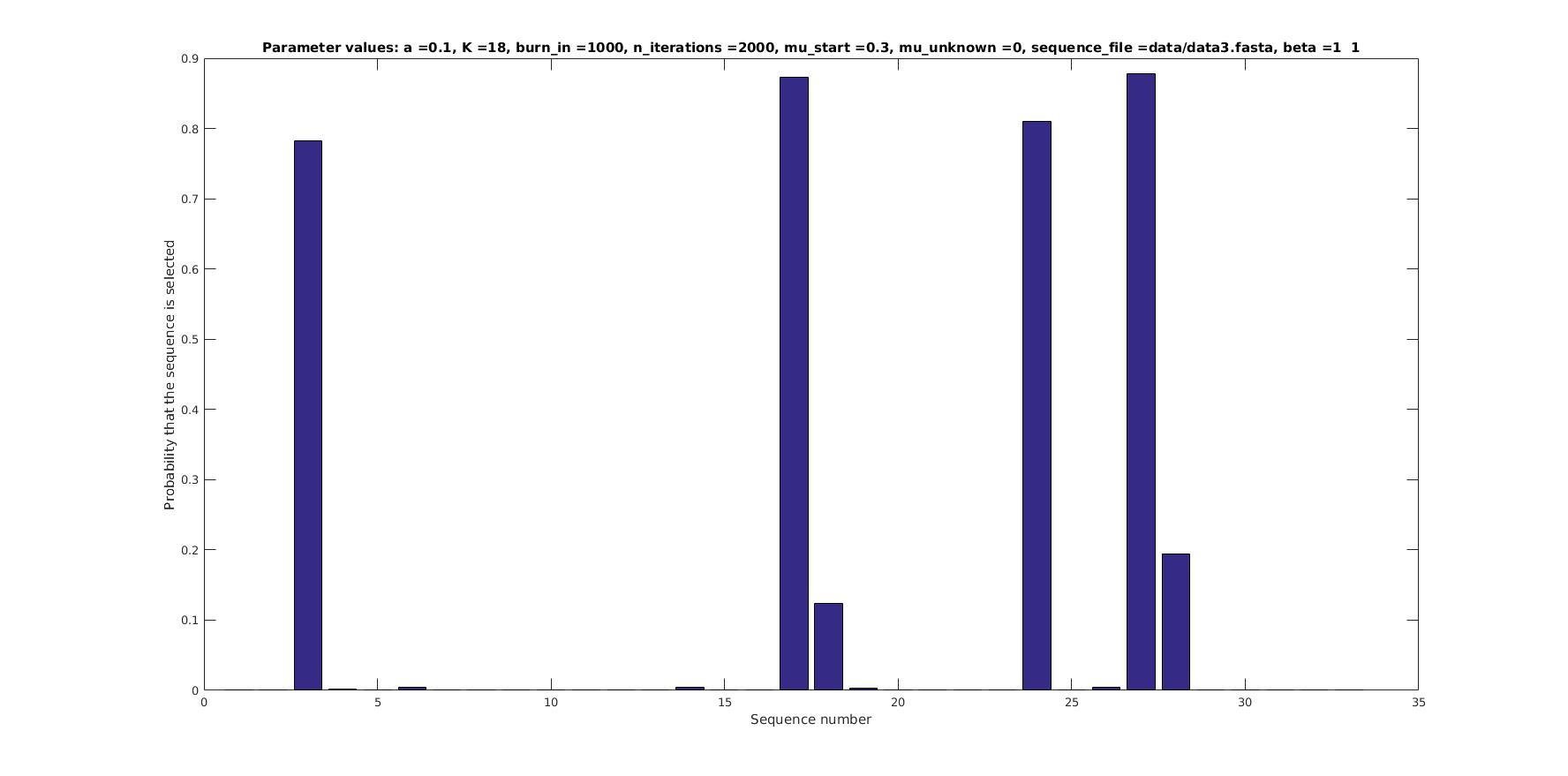
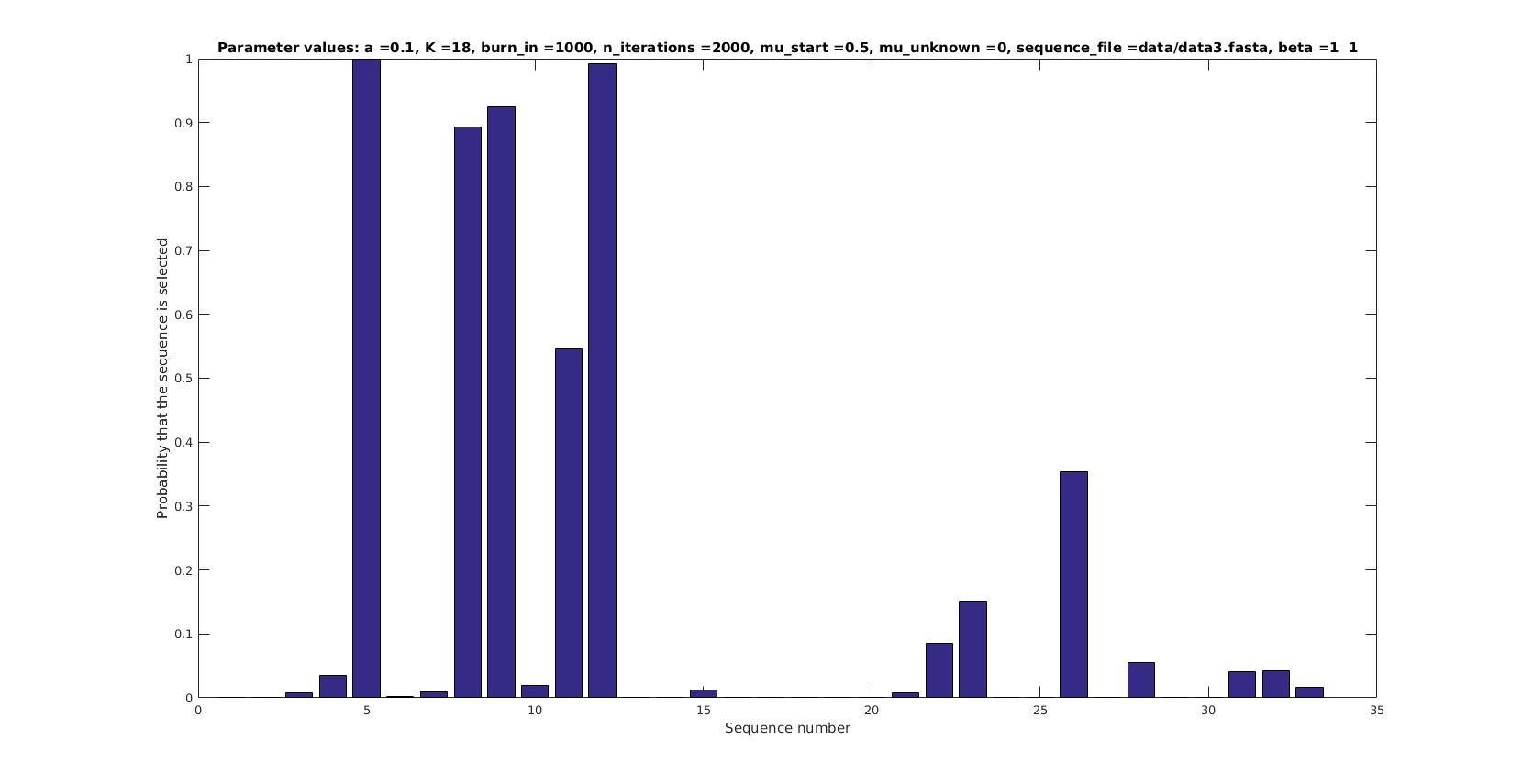
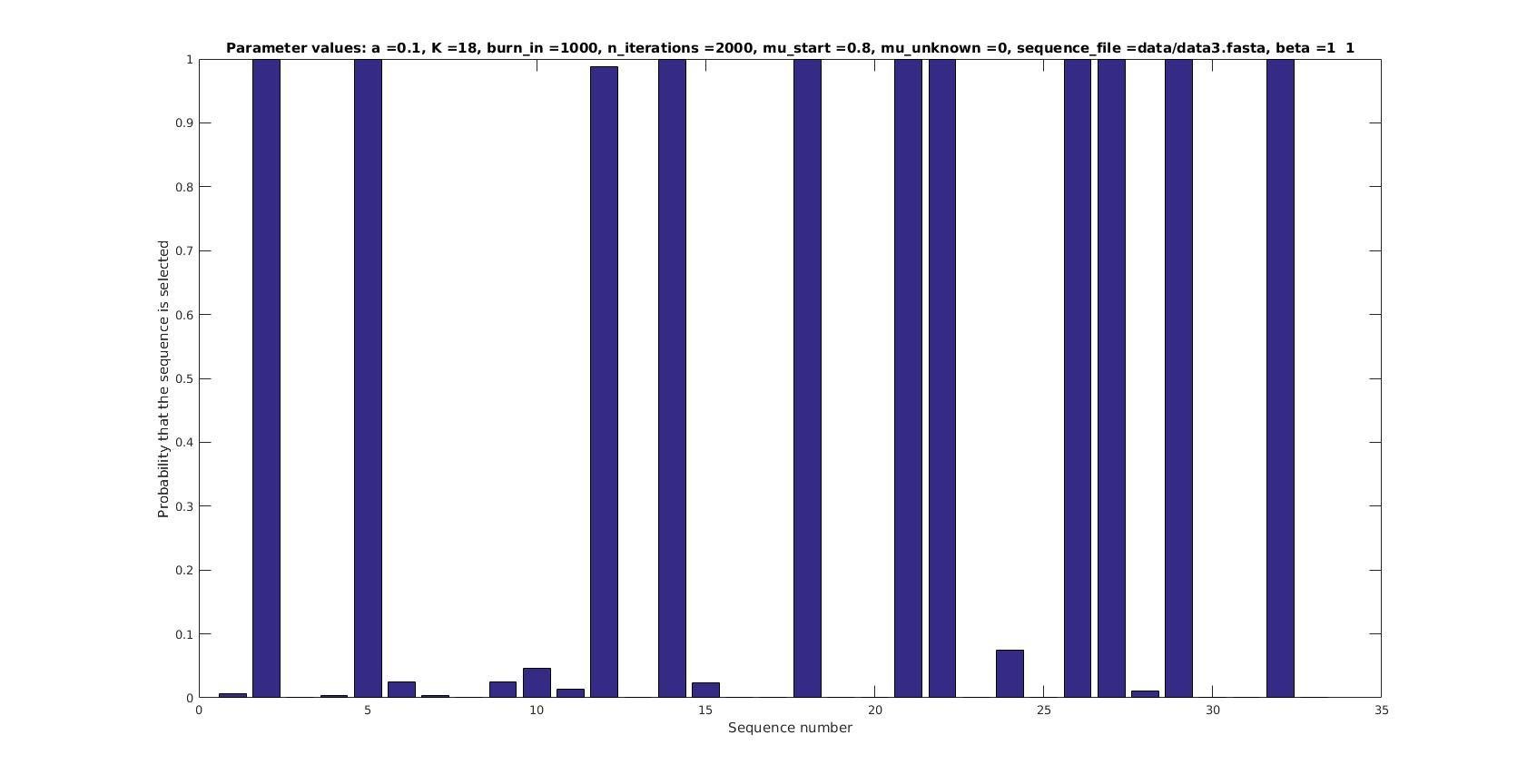
Selected sequences

\frac{5}{33}
533\frac{5}{33}

Actual fraction of

selected sequences:

Sequence number

Sequence number

Sequence number

Probability that sequence is selected

Probability that sequence is selected

Probability that sequence is selected

\mu = 0.3
μ=0.3\mu = 0.3
\mu = 0.5
μ=0.5\mu = 0.5
\mu = 0.8
μ=0.8\mu = 0.8
\mu = 1
μ=1\mu = 1

1

0.9

1

0.9

0.5

0.45

1

0.9

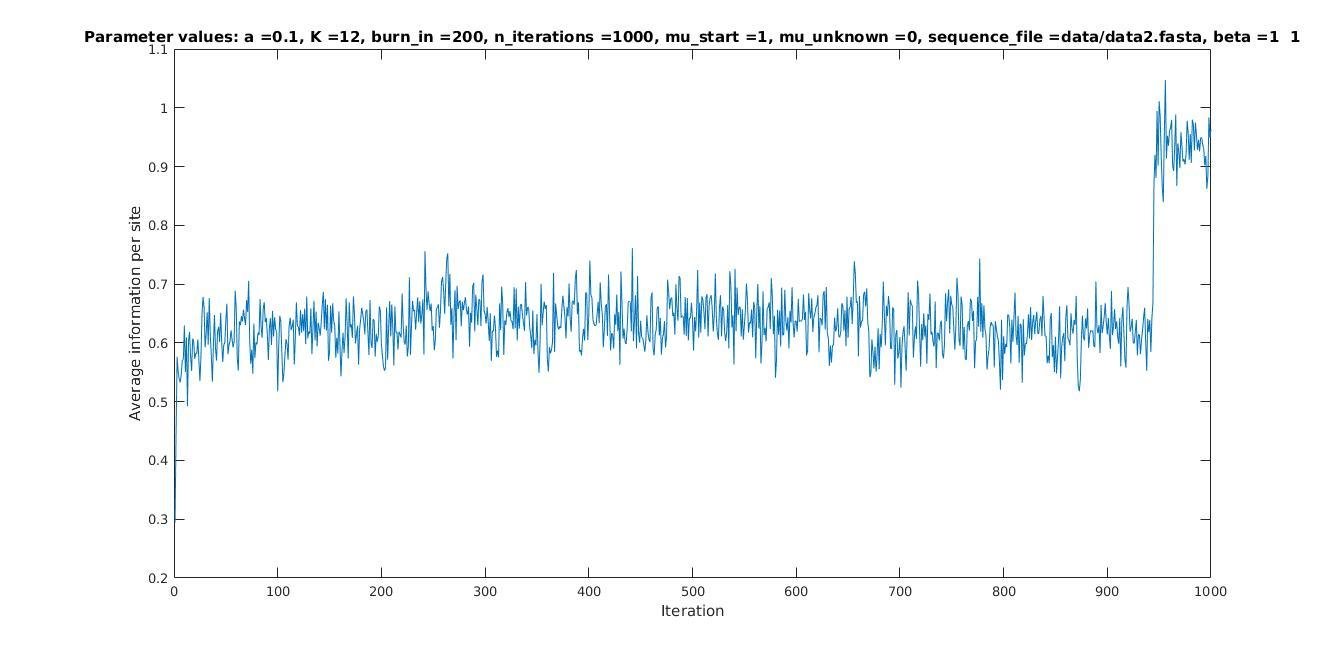
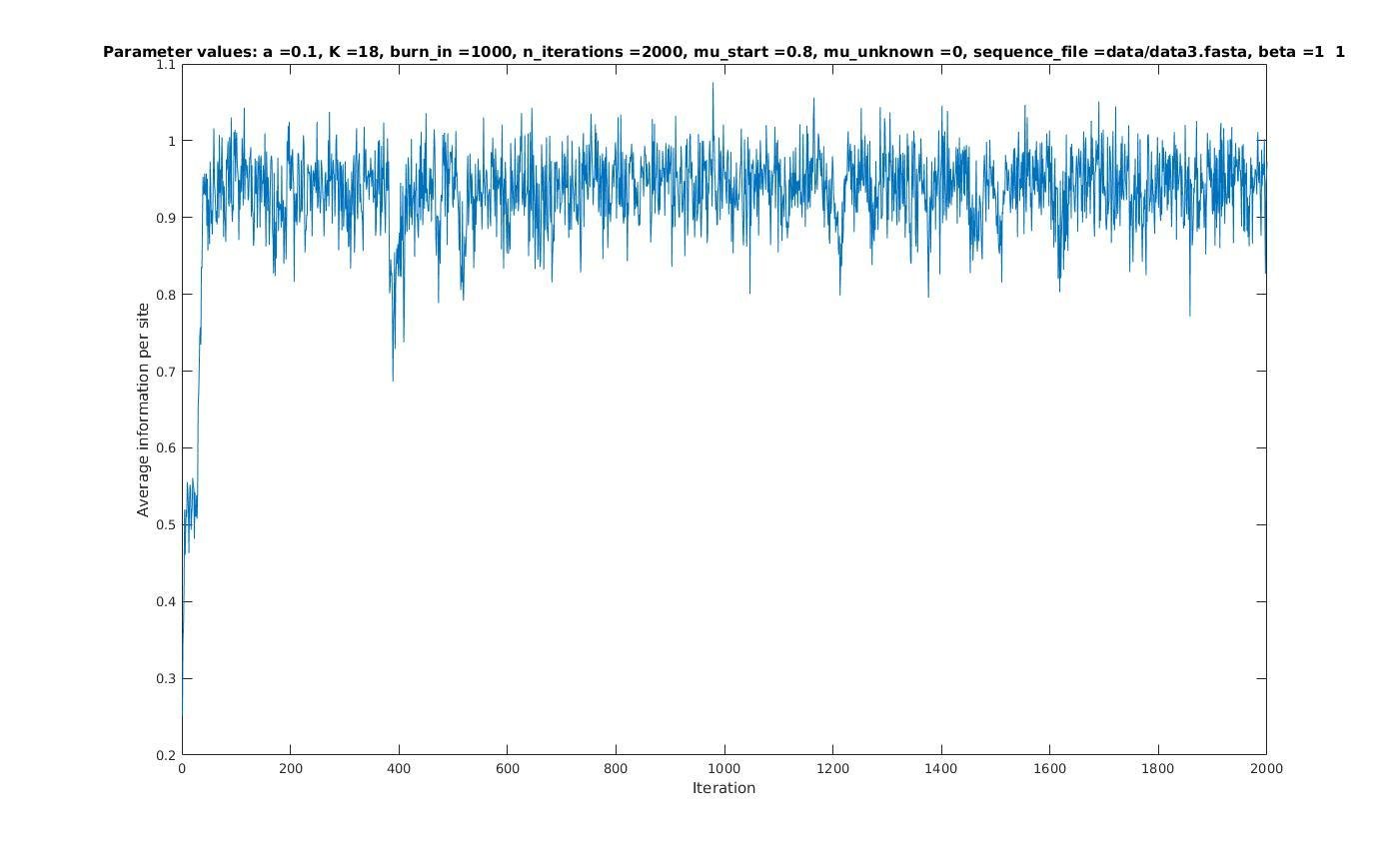
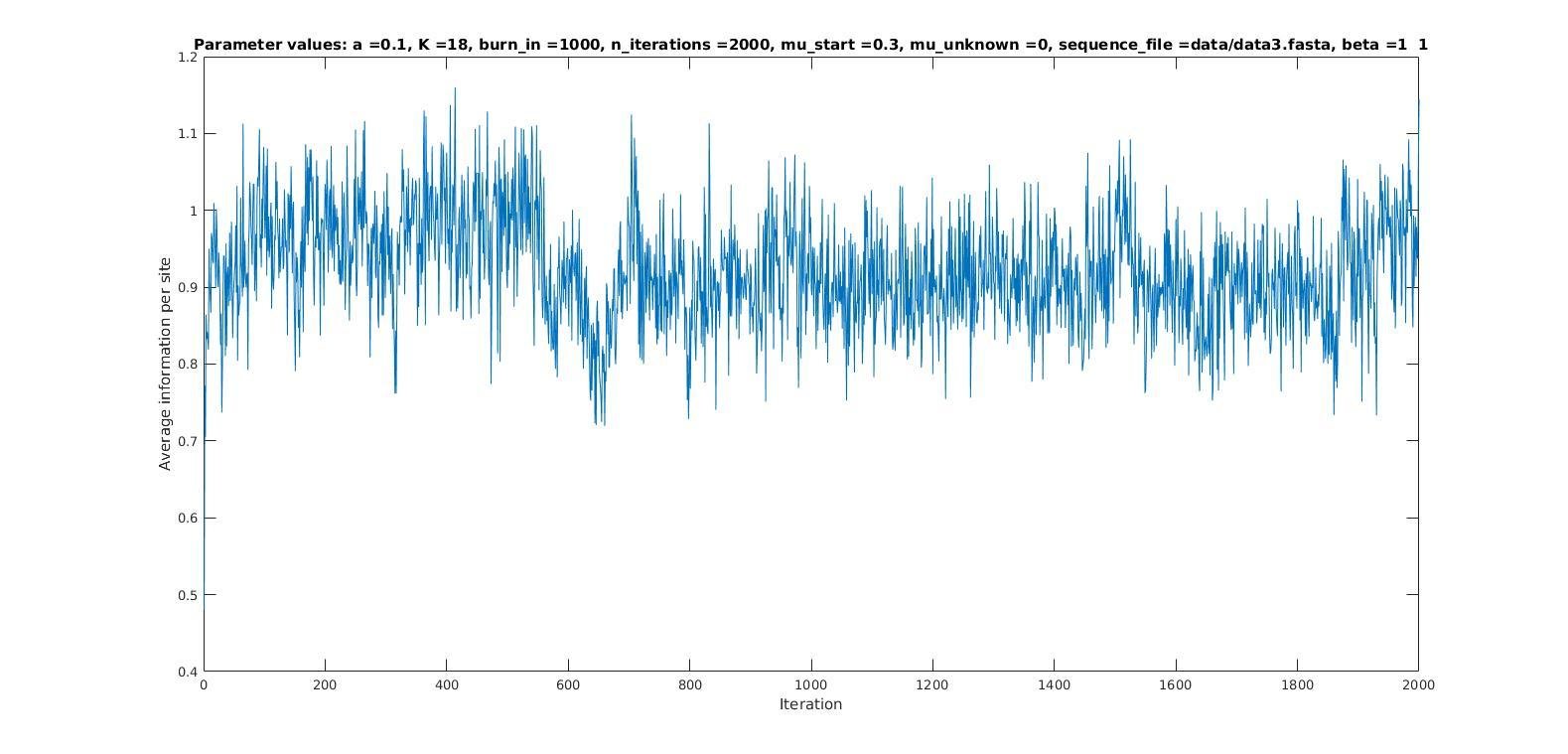
Average information per site versus iteration

\mu = 0.3
μ=0.3\mu = 0.3
\mu = 0.8
μ=0.8\mu = 0.8

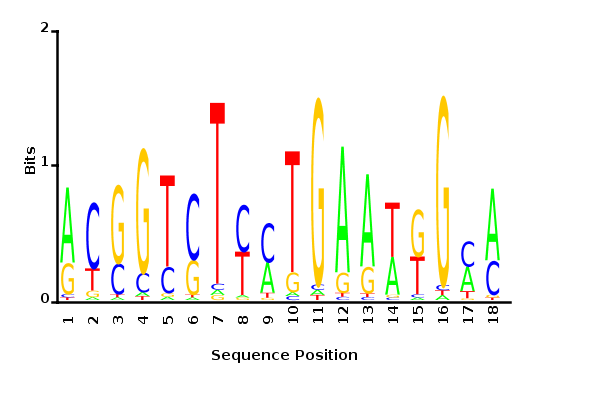
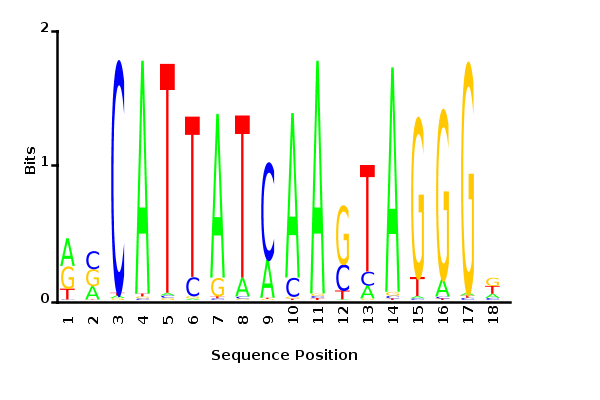
Probability weight matrices

Bayesian inference on the motif probability

p(\mu | z) \propto \mu^{\beta_0 + \sum_i z_i}(1-\mu)^{\beta_1 + N - \sum_i z_i}
p(μ∣z)∝μβ0+∑izi(1−μ)β1+N−∑izi p(\mu | z) \propto \mu^{\beta_0 + \sum_i z_i}(1-\mu)^{\beta_1 + N - \sum_i z_i}
p(z|\mu) \propto \mu^{\sum_i z_i}(1-\mu)^{\sum_i(1-z_i)}
p(z∣μ)∝μ∑izi(1−μ)∑i(1−zi)p(z|\mu) \propto \mu^{\sum_i z_i}(1-\mu)^{\sum_i(1-z_i)}

Likelihood:

Prior:

Posterior:

p(\mu) \propto \mu^{\beta_0} (1-\mu)^{\beta_1}
p(μ)∝μβ0(1−μ)β1 p(\mu) \propto \mu^{\beta_0} (1-\mu)^{\beta_1}
\sim Bin (N, \mu)
∼Bin(N,μ) \sim Bin (N, \mu)
\small \sim Beta (\beta_0, \beta_1)
∼Beta(β0,β1) \small \sim Beta (\beta_0, \beta_1)
\small \sim Beta (\beta_0 +\sum_i z_i, \beta_1 + N -\sum_i z_i)
∼Beta(β0+∑izi,β1+N−∑izi)\small \sim Beta (\beta_0 +\sum_i z_i, \beta_1 + N -\sum_i z_i)
\mu
μ\mu

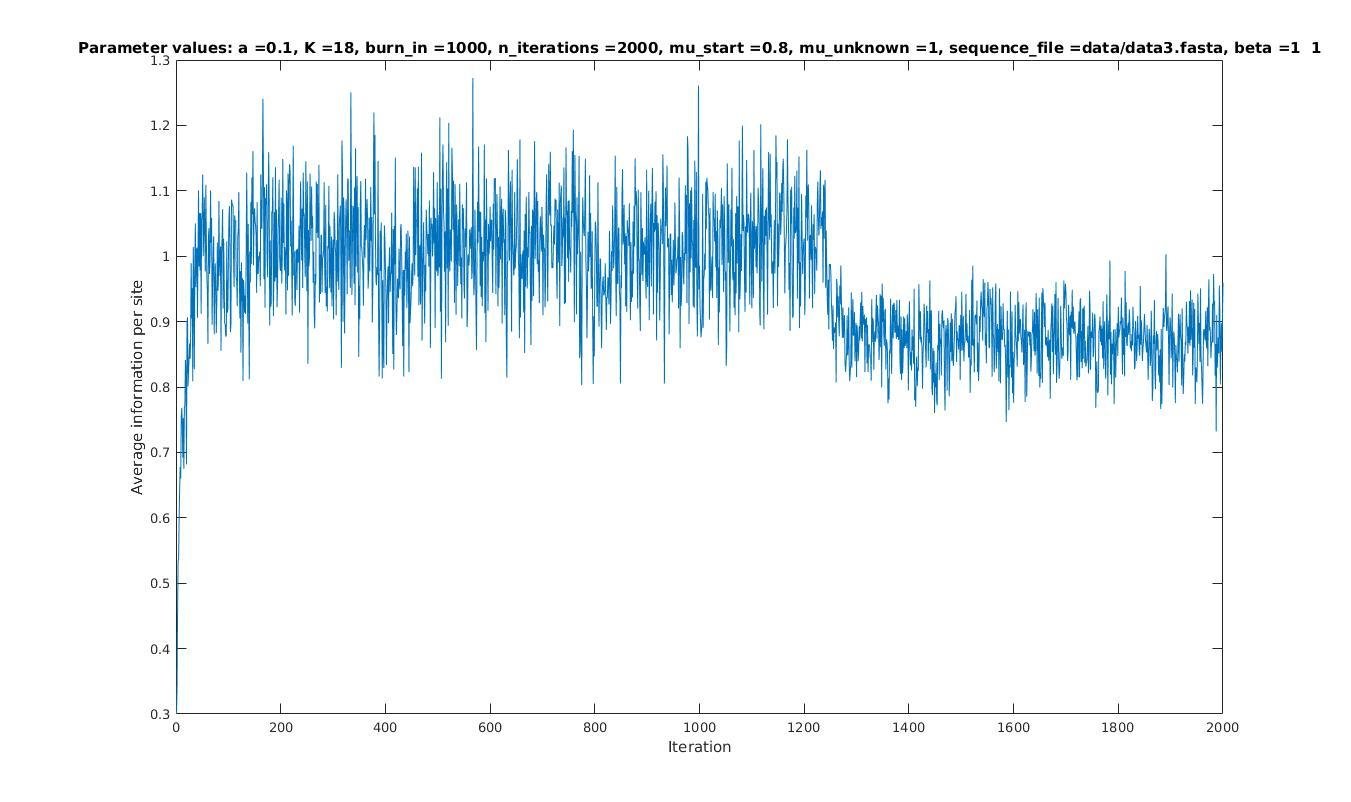
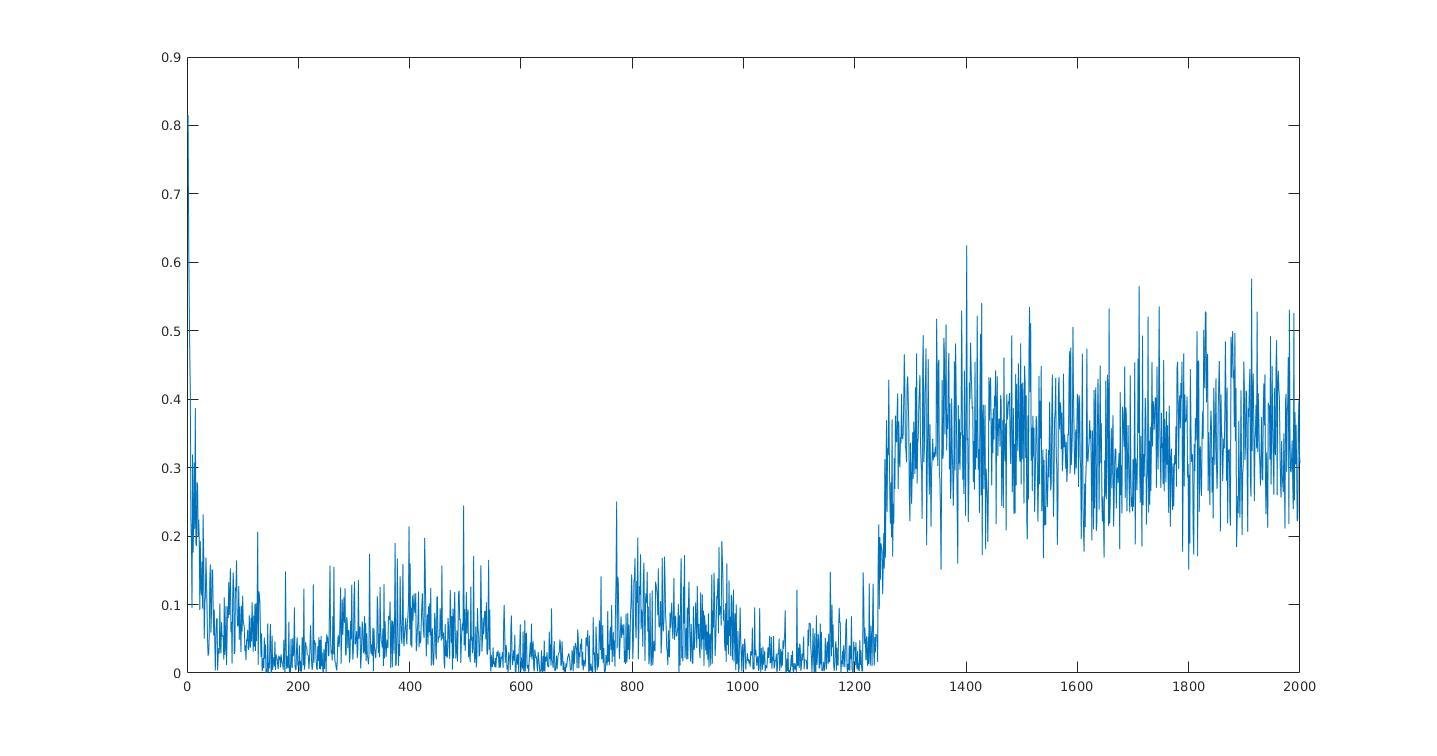
Average information

per site

Iterations

Iterations

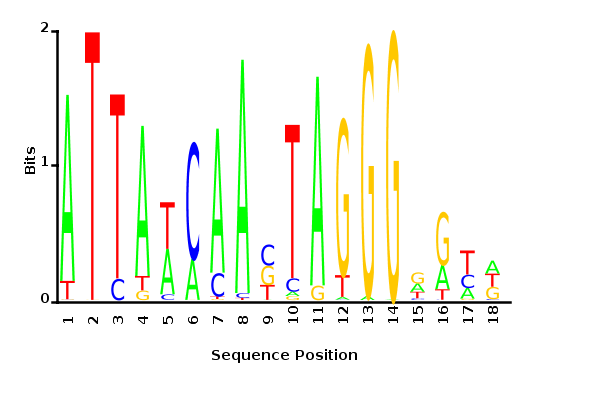
Maximum likelihood-ratio PWM

Analysis of parameter a

\mu = 0.3
μ=0.3\mu = 0.3
a = 1
a=1a = 1
\mu = 0.5
μ=0.5\mu = 0.5
\mu = 0.8
μ=0.8\mu = 0.8

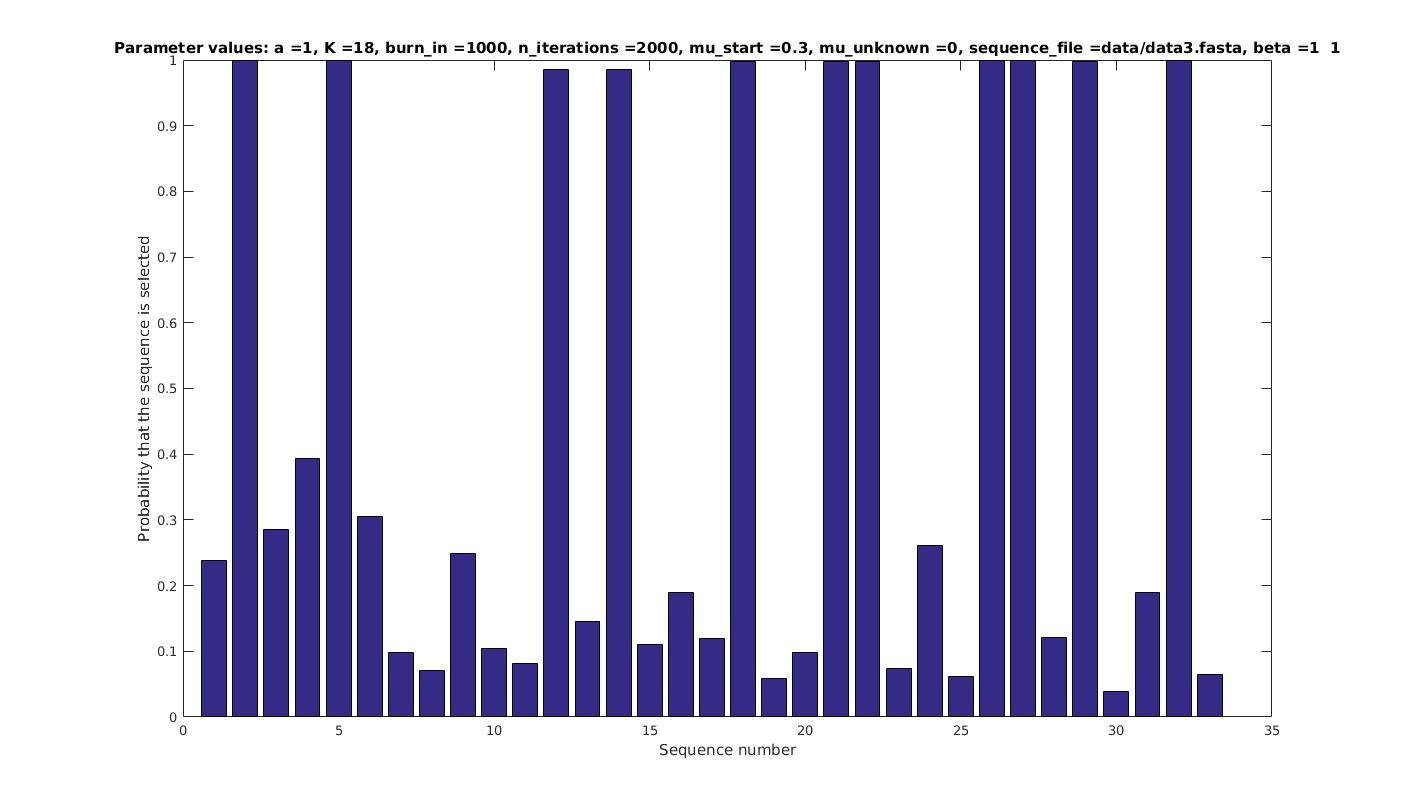
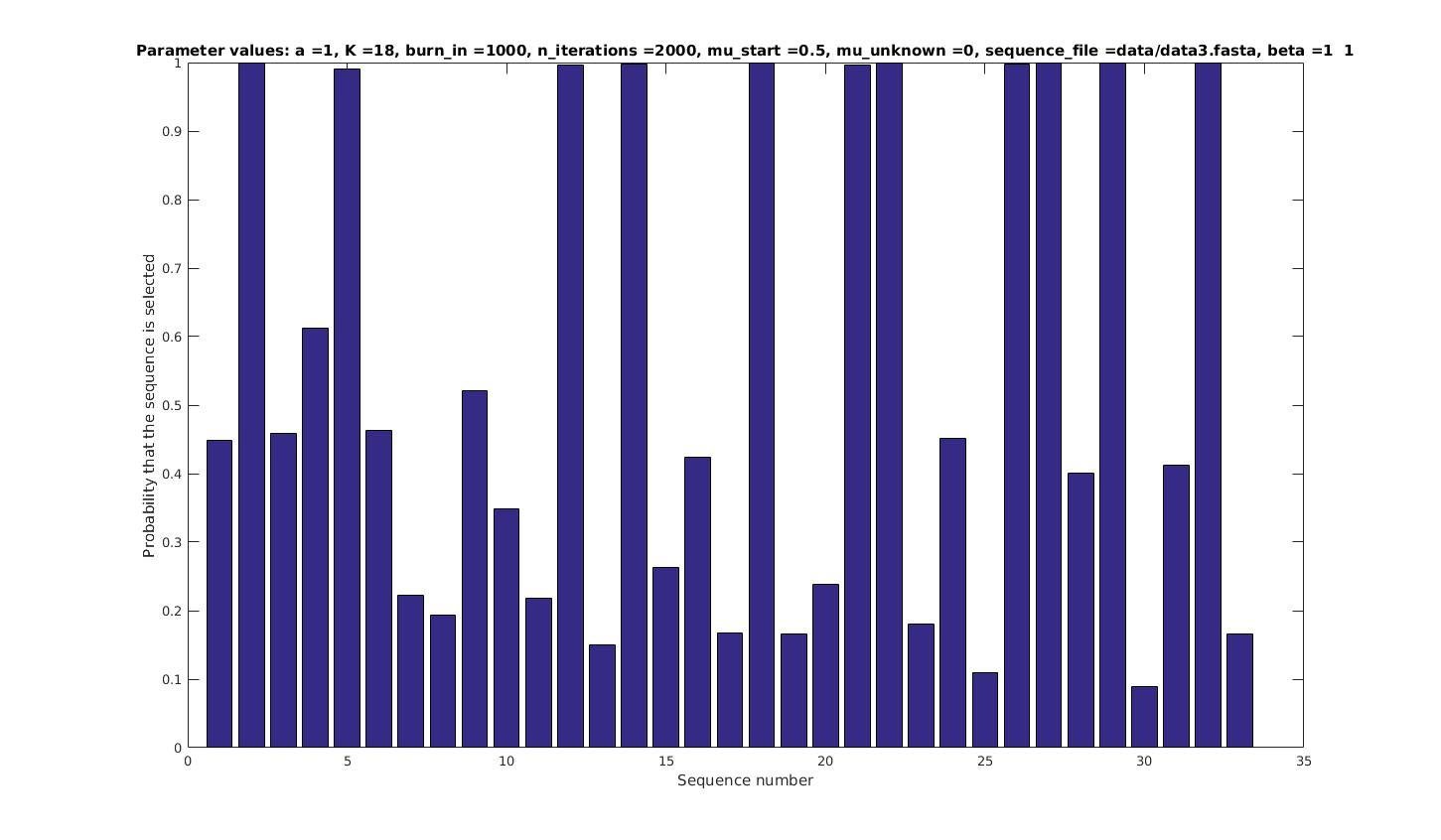
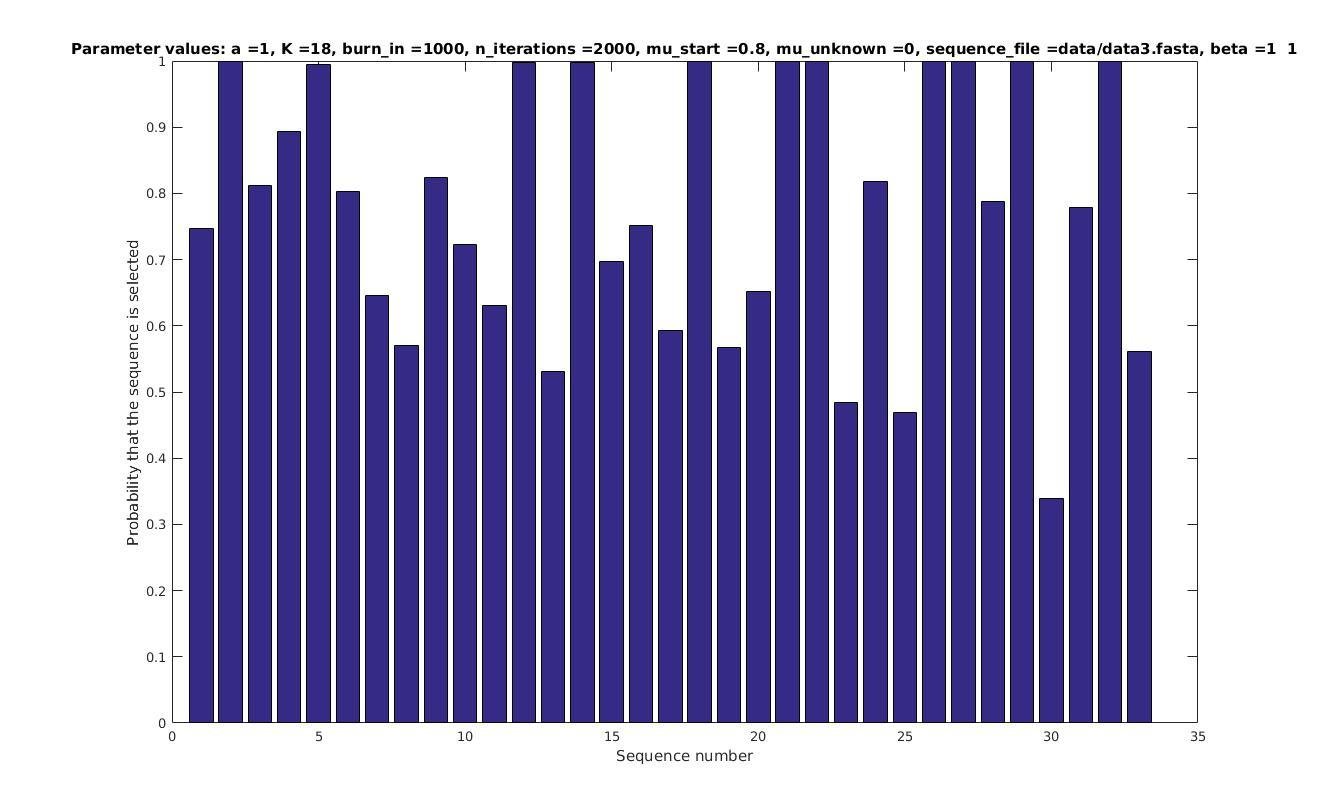
Selected sequences

Sequence number

Sequence number

Sequence number

Probability that sequence is selected

Probability that sequence is selected

Probability that sequence is selected

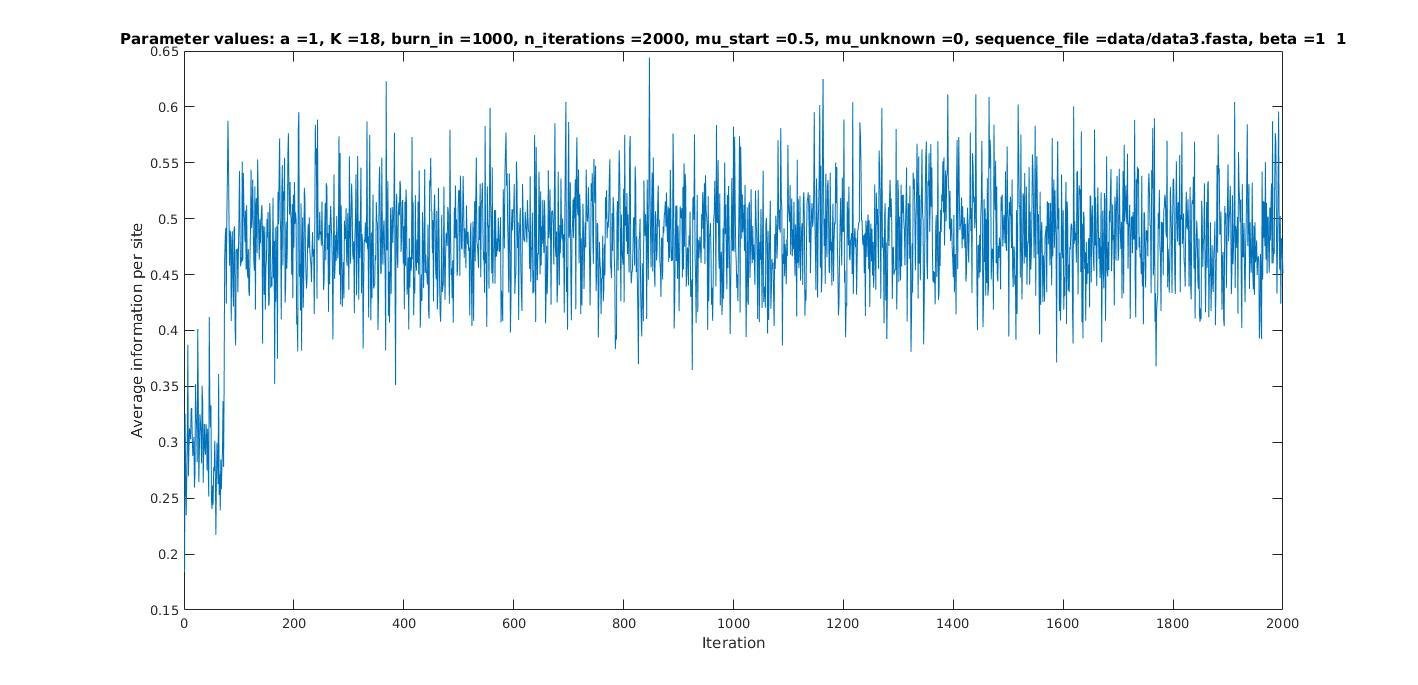
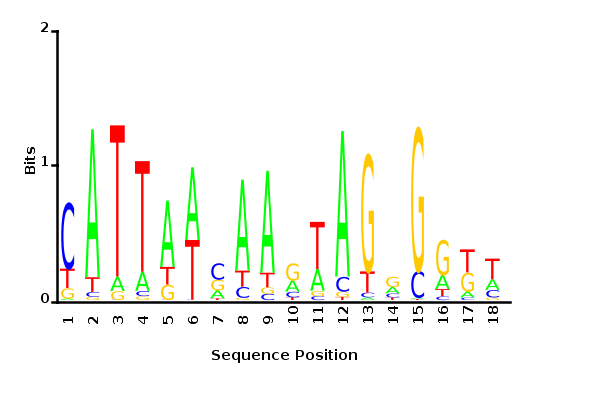
Average information

per site

Iterations

0.5

Accounting for phylogenetic relations

We are given phylogenetic tree

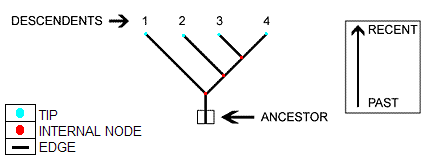
We model evolution for each base pair independently, using the Felsenstein model

We assume the motif represented by M, is the ancestor of all current sequences

Can then use a recursive algorithm for computing the likelihood

P_{\text{Fels}}(\{X\}\mid M,s)
PFels({X}∣M,s)P_{\text{Fels}}(\{X\}\mid M,s)
P_{\text{Fels}}(\{X\}\mid M,s) P(M\mid s)
PFels({X}∣M,s)P(M∣s)P_{\text{Fels}}(\{X\}\mid M,s) P(M\mid s)

Problem

now has a very complicated functional form

Solution: Metropolis-Hastings

Sample using proposal probability

Accept with probability

\min\{1,\frac{P_{\text{Fels}}(\{X\}\mid M',s)\prod\limits_{b\in \{A,C,G,T\}}(M'_b)^f}{P_{\text{Fels}}(\{X\}\mid M,s)P(M\mid s)\prod\limits_{b\in \{A,C,G,T\}}(M_b)^f}\}
min{1,PFels({X}∣M′,s)∏b∈{A,C,G,T}(Mb′)fPFels({X}∣M,s)P(M∣s)∏b∈{A,C,G,T}(Mb)f}\min\{1,\frac{P_{\text{Fels}}(\{X\}\mid M',s)\prod\limits_{b\in \{A,C,G,T\}}(M'_b)^f}{P_{\text{Fels}}(\{X\}\mid M,s)P(M\mid s)\prod\limits_{b\in \{A,C,G,T\}}(M_b)^f}\}
P(M^{(k)}\mid\{X\},s) \sim Dirichlet(\alpha + f(k,s,\{X\})
P(M(k)∣{X},s)∼Dirichlet(α+f(k,s,{X})P(M^{(k)}\mid\{X\},s) \sim Dirichlet(\alpha + f(k,s,\{X\})

this should converge to samples from full posterior

Directly inferring K

Try to sample K

P(M,K\mid \{X\},s) \propto P(\{X\}\mid M,K,s) P(M\mid s) P(K)
P(M,K∣{X},s)∝P({X}∣M,K,s)P(M∣s)P(K)P(M,K\mid \{X\},s) \propto P(\{X\}\mid M,K,s) P(M\mid s) P(K)

Can't find the normalization constant, so use Metropolis-Hastings

Prior for K?

Geometric distribution has maximum entropy for positive integers.

But, K is constrained to be smaller than a certain value, given the sequences, and the starting positions s.

Made with Slides.com