Genotype-phenotype-like maps

in adaptive systems

Adaptive systems

Evolving systems

Learning systems

Supervised learning

Genotype-phenotype-like maps

(GP maps)

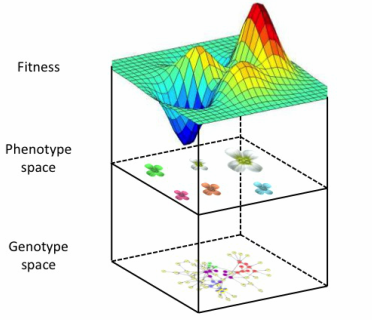
Cost

Function space

Parameter space

GP map

GP maps

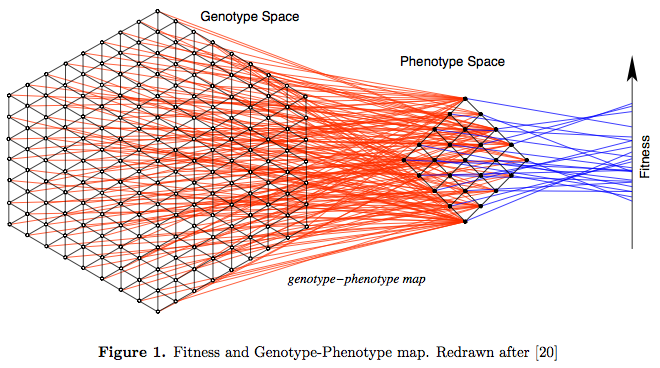
  • Redundancy

  • Bias

  • Robustness

  • Evolvability

  • Neutral networks

  • etc

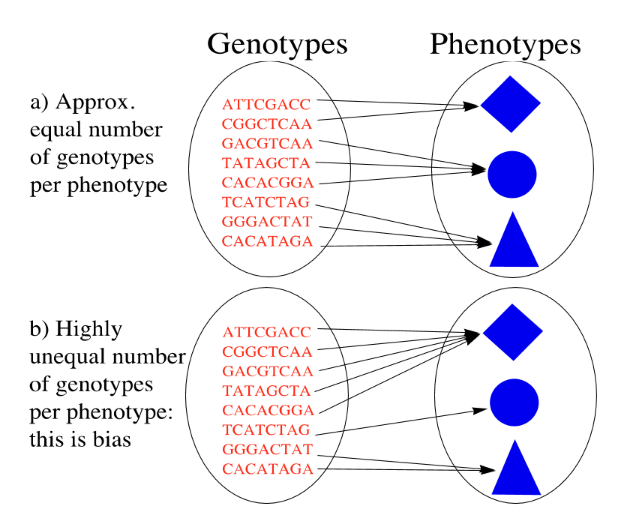
Properties

Redundancy & Bias

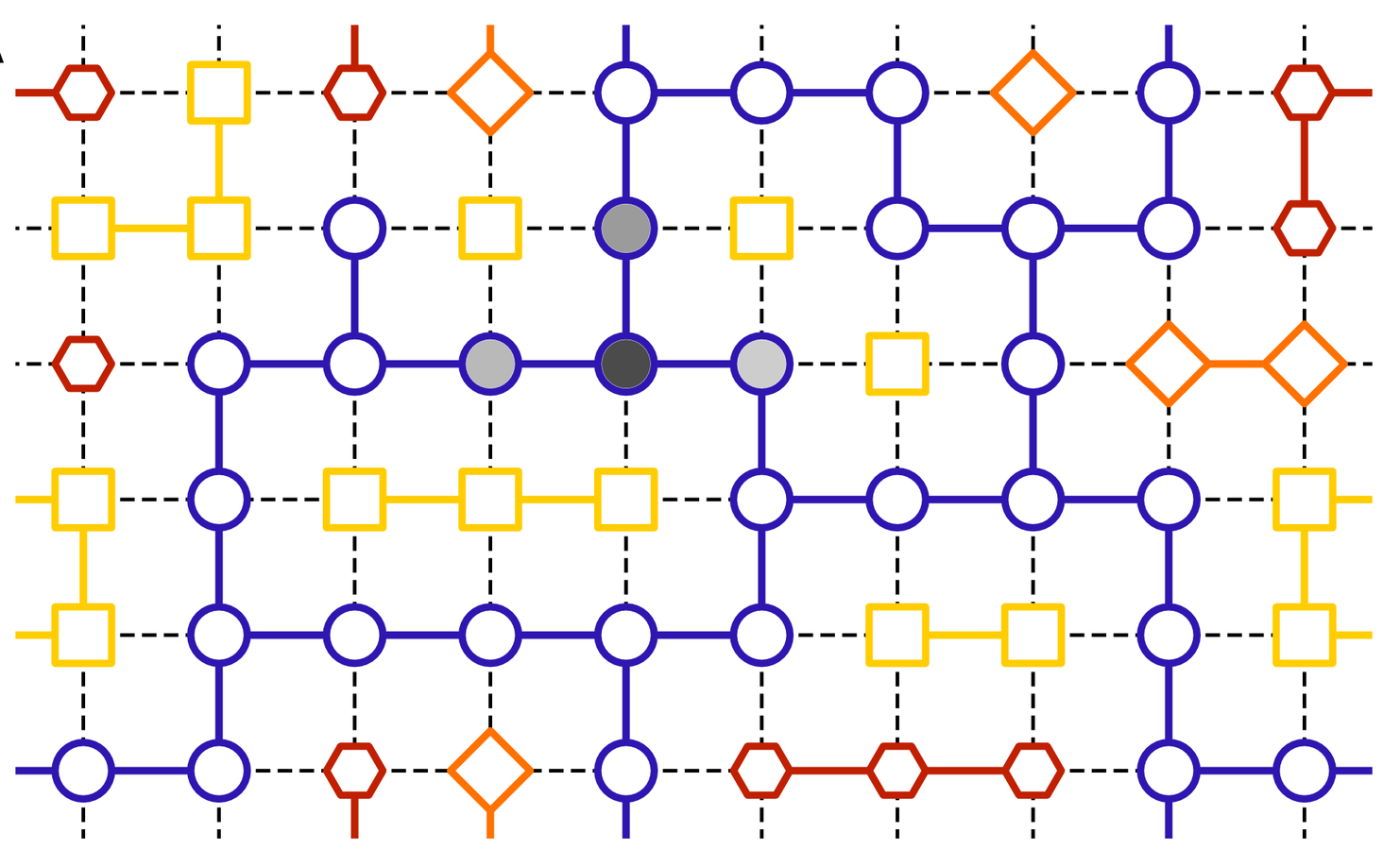
Robustness

Again, many analogies in learning theory

Algorithmic Information Theory  and simplicity bias

100101010001011101110101110111010101

Kolmogorov complexity

100101010001011101110101110111010101

Simplicity bias

100101010001011101110101110111010101

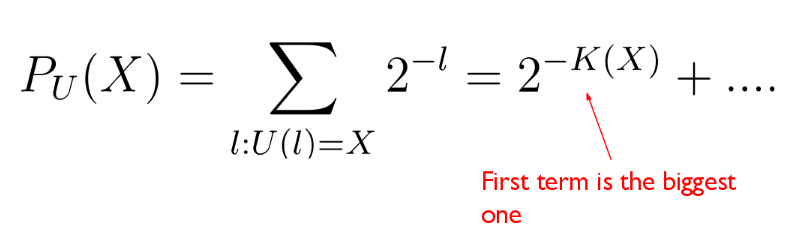
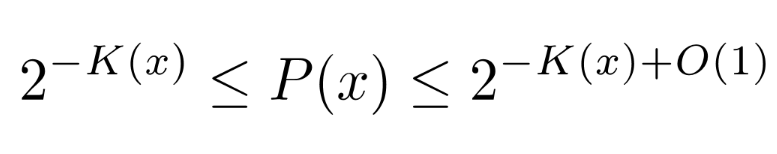
Intuition: simpler outputs are much more likely to appear

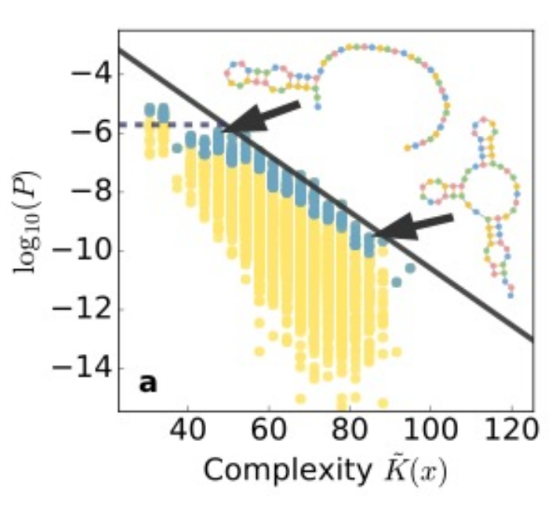
Computable simplicity bias

100101010001011101110101110111010101

Turing machine --> Finite-state transducers

Kolmogorov complexity --> Lempel-Ziv complexity

Everything is now computable,

and can be analyzed theoretically.

Keywords: data compression, universal source coding

Can we do similar analysis for future systems we will be studying?

Other complexity measures

100101010001011101110101110111010101
  • Coding theorem methods (Hector Zenil)
  • Krohn-Rhodes complexity
  • Entropy
  • Other compression-based complexities
  • ...

Universal induction

100101010001011101110101110111010101

Optimal learning

Learning theory

Supervised learning

f: Y \to X
f:Y→Xf: Y \to X
\{(x_i,f(x_i))\}_{i=1,...,m}
{(xi,f(xi))}i=1,...,m\{(x_i,f(x_i))\}_{i=1,...,m}

Learn

Given

Neural networks

f(\mathbf{x}) = \sigma_3 (\mathbf{b_3} + \mathbf{W_3} \sigma_2 (\mathbf{b_2} + \mathbf{W_2} \sigma_1 (\mathbf{b_1} + \mathbf{W_1} \mathbf{x})))
f(x)=σ3(b3+W3σ2(b2+W2σ1(b1+W1x)))f(\mathbf{x}) = \sigma_3 (\mathbf{b_3} + \mathbf{W_3} \sigma_2 (\mathbf{b_2} + \mathbf{W_2} \sigma_1 (\mathbf{b_1} + \mathbf{W_1} \mathbf{x})))

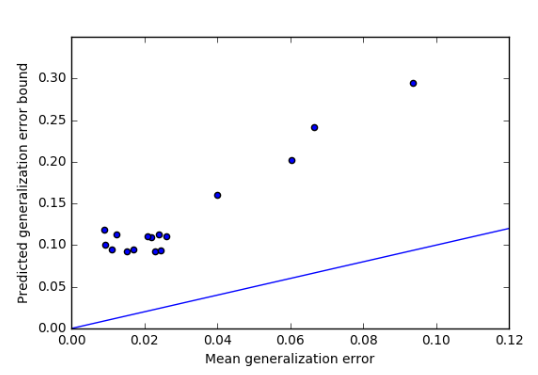
PAC-Bayes

Good framework to study the effect of GP map biases on successful learning/evolution

like betting on some solutions more than on others

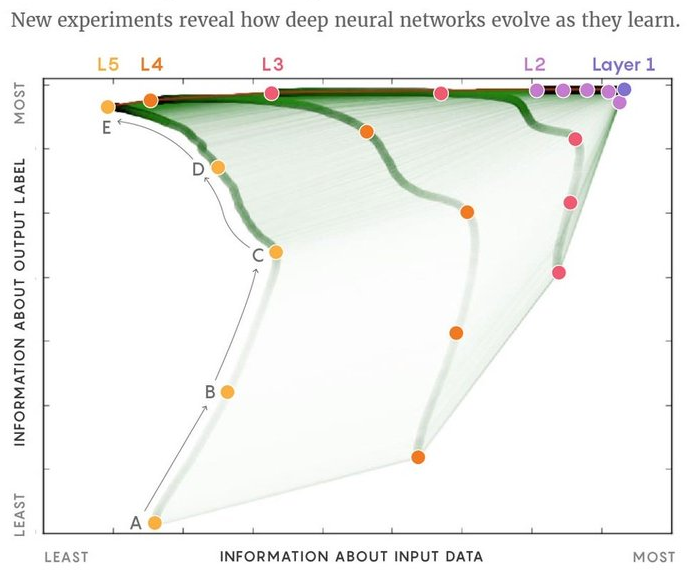
Information bottleneck

Compressing the input could help successful learning

I'm exploring ways of connecting it to VC dimension of neural nets

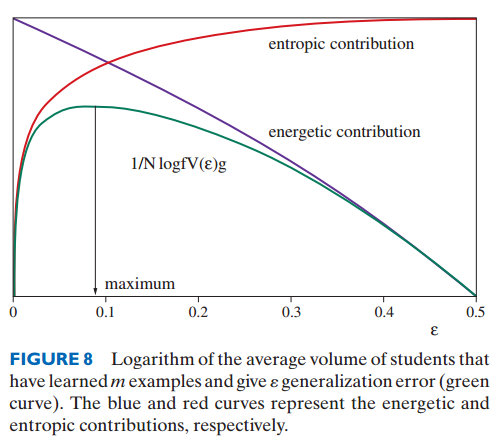
Statistical physics framework

Average/typical case instead of worst case

Conclusion

Adaptive systems

GP maps

Information theory

Learning theory

depend on

studied with

studied with

Applications

  • Biological GP maps
    • Protein self-assembly
    • Gene-regulatory networks
    • Developmental models
    • Neural networks
  • Machine learning
    • Understanding generalization in deep learning
    • Universal AI?
  • Artificial and natural evolution
  • Sloppy systems
  • Understanding a bit more how the world works:)
Made with Slides.com